黄土高原坡地土壤与旋耕部件互作离散元仿真参数标定
孙景彬 刘 琪 杨福增 刘志杰 王 峥
(1.西北农林科技大学机械与电子工程学院, 陕西杨凌 712100;2.农业农村部北方农业装备科学观测实验站, 陕西杨凌 712100;3.西北农林科技大学林学院, 陕西杨凌 712100)
0 引言
我国黄土高原丘陵区是黄土高原重要农业区,该地区光照充足,适合种植小麦、玉米、马铃薯、谷子和荞麦等农产品[1]。农作物播种前的旋耕作业是黄土高原坡耕地种植粮食作物时重要耕作工序之一[1-2],因此,研发适用于坡地作业的专用高性能旋耕装备来减少坡地土壤的耕作侵蚀、有效保持水土,对促进黄土高原地区农业的发展至关重要。设计高效作业机具的首要前提是明确坡地土壤与触土部件间的互作用机制,土槽、田间试验只能分析土壤宏观扰动状况,不能从微观的角度去剖析运动规律[3],大量研究表明,离散元法可以模拟分析土壤颗粒与农具部件之间的互作用关系,可为机具设计提供新的方法[4],然而,农具部件与土壤之间的相互作用受到土壤性质及土壤动态作用的直接影响,对于不同类型的土壤,其影响效应差异显著,因此,在基于离散元法开展农具部件与土壤互作关系研究之前,对土壤颗粒间、土壤与触土部件间的仿真参数进行标定是首要工作。
目前,国内外专家学者基于离散元法在土壤参数标定、土壤-机器互作关系研究等方面做了一定研究。UCGUL等[5]综合Hertze-Mindlin及Hysteretic Spring典型模型研究了土壤颗粒间的粘结力对其塑性形变的影响规律;AIKINS等[6]整合Hysteretic Spring模型和Linear Cohesion模型对高粘度土壤的静摩擦因数和滚动摩擦因数进行了标定,并经开沟试验验证了参数标定的准确性;ZENG等[7]建立了土壤-农具-秸秆残茬相互作用的离散元仿真模型,并以4种不同的铲进行仿真试验和土槽试验,最终验证模型的有效性;MILKEVYCH等[8]基于离散法建立了除草过程中土壤与触土部件相互作用引起土壤位移的研究模型,模拟试验和实测试验表明土壤位移具有一致性;UCGUL等[9]采用离散元法模拟了土壤与板型犁之间的相互作用,经仿真试验与实地试验比较耕作牵引力以及犁沟剖面,结果表明离散元法精度可靠。石林榕等[10]基于延迟弹性模型和线性粘附模型的优点对6种含水率的农田土壤进行模型参数标定,经鸭嘴插穴试验验证了模型的有效性;张锐等[11]基于Hertz-Mindlin模型,经过堆积角试验完成沙土颗粒的模型参数标定;李俊伟等[12]基于Hertz-Mindlin with JKR Cohesion 模型标定了东北黑土颗粒接触参数及其与触土部件间接触参数,为高含水率黏土参数标定提供参考;向伟等[13]经堆积试验完成了南方黏壤土的仿真参数标定,成穴试验验证了标定参数的有效性;田辛亮等[14]选用Hertz-Mindlin with JKR接触模型对黑土区玉米秸秆-土壤混料的离散元仿真接触参数进行标定,试验验证了仿真模型参数的可靠性。
上述土壤参数标定的研究主要是针对沙土、东北黑黏土、海南砖红黏土等土壤类型,并以特定的作业工况为研究目标,对于黄土高原典型坡地粘壤土并不适用。因此,本文针对典型坡地土壤与旋耕部件互作机理探究缺乏准确可靠离散元仿真模型参数,以及坡地旋耕作业耕作侵蚀现象严重的现实问题,拟选取Hertz-Mindlin with JKR Cohesion为接触模型,采用仿真试验与物理试验结合的方法,对土壤颗粒之间以及土壤颗粒与旋耕刀材料65Mn钢间的离散元仿真参数进行标定,并基于自主研发的丘陵山地履带拖拉机进行坡地旋耕田间试验和仿真试验,以期获得准确可靠的坡地旋耕土壤离散元仿真参数。
1 土壤颗粒仿真模型参数标定
1.1 接触模型选取
黄土高原坡地以粘壤土居多,经调研和文献[15]知该区域土壤含水率一般为10%~15%。鉴于本文的接触模型建立主要是为后续坡地土壤-旋耕刀互作机理研究做铺垫,故接触模型的选取需充分考虑模型间的粘结力对颗粒运动的影响。
离散元法中的Hertz-Mindlin接触模型只考虑了颗粒的弹性形变,没有涉及颗粒间粘结力影响[3],故不能准确模拟土壤在旋耕部件扰动下的运动行为;Hertz-Mindlin with Bonding 接触模型适用于粘结颗粒且广泛使用[16-18],但该模型是基于粘结键将颗粒吸附在一起,粘结键在外力作用下断裂后颗粒会单独存在,这与实际情况不相符,严重影响仿真结果,此模型较适合模拟材质较为坚硬的物料,如混凝土、岩石等[11];Hertz-Mindlin with JKR接触模型是粘结性颗粒接触模型,考虑了颗粒粘结力对其运动的影响,适用于模拟有一定水分或静电存在的物料(如具有一定湿度的土壤等)[19-22],故选用Hertz-Mindlin with JKR接触模型,其具体架构参照文献[3]。
1.2 模型参数类型及标定
离散元仿真模型中参数类型有材料本征参数、材料接触参数和接触模型参数。材料本征参数是指材料自身特征参数,可通过试验或查阅文献获得;材料接触参数可经试验测定或仿真试验标定得到;接触模型参数主要是JKR表面能,对于坡地旋耕土壤,研究其在旋耕刀扰动下的运动规律要考虑土壤颗粒间粘结力的影响,故需标定JKR表面能。
1.2.1试验材料及其本征参数
采用Mastersizer 2000型激光粒度仪(图1a)对土壤样本的粒级百分含量进行检测,结果显示:粘粒(粒径d<0.002 mm)占比23.11%,粉粒(0.002 mm≤d≤0.02 mm)占比30.78%,砂粒(0.02 mm≤d≤2 mm)占比46.11%,按照文献[23]中的“国际制土壤质地分类三角图”方法对土壤类型进行划分,可得土壤类型属于黄土高原典型的粘壤土。采用图1b所示的奥豪斯MB23型水分快速分析仪(美国)实测0~200 mm深度土层平均含水率为13.4%±1%;采用环刀(容积2×10-4m3)取土和电子天平(量程500 g、精度0.001 g)测量土壤的湿密度,试验重复10次求均值,将1 210 kg/m3作为最终仿真参数。
采用筛析法[24]对土壤的颗粒度进行分析,首先用奥豪斯MB23型水分快速分析仪(图1b)将土样干燥至恒质量并研碎土壤固结体,使用不同孔径的标准检验筛在土壤振筛机(图1c)上进行筛分,得到粒径大于4 mm、1~4 mm、0~1 mm的土壤占比分别为25.61%、19.84%、54.55%。离散元仿真中,土壤颗粒粒径、形状会较大程度地影响仿真结果和效率[25]。因此,为保证离散元仿真的可靠性,仿真试验中设置土壤粒径及百分比:4 mm土壤颗粒25.61%,2.5 mm土壤颗粒19.84%,1 mm土壤颗粒54.55%。为了提高离散元仿真的效率,利用EDEM软件中的球形颗粒替代不同形状类型的颗粒。

图1 土壤本征参数测量仪器Fig.1 Measuring instruments for soil intrinsic parameters
根据广义胡克定律可以推导出侧压力系数与泊松比的关系[10]为
(1)
式中ν——泊松比K0——侧压力系数
侧压力系数与内摩擦角间关系[10,26]为
K0=1-sinφ
(2)
式中φ——内摩擦角,直剪试验测得为19.9°
通过计算得到试验土壤样品的泊松比为0.40;参照文献[18]设定土壤剪切模量为1×106Pa。
1.2.2土壤堆积角物理试验
配置含水率为13.4%±1%的土壤,搭建如图2a所示堆积角测定试验台,选用的漏斗口径为25 mm,漏斗顶部直径230 mm,高为210 mm,将其固定于专用铁架台一侧,漏斗出口与接料底板间距100 mm。开始堆积角试验前,先将漏斗出口堵住,将试验土壤倒入,打开漏斗口让土壤自然流出,待土壤全部流出静置后,使用手持式量角器随机从堆形的5个方位测量堆积角取均值,作为1次试验的测量值,如图2b所示,共重复5次试验取均值得到含水率13.4%±1%的土壤堆积角为43.25°。
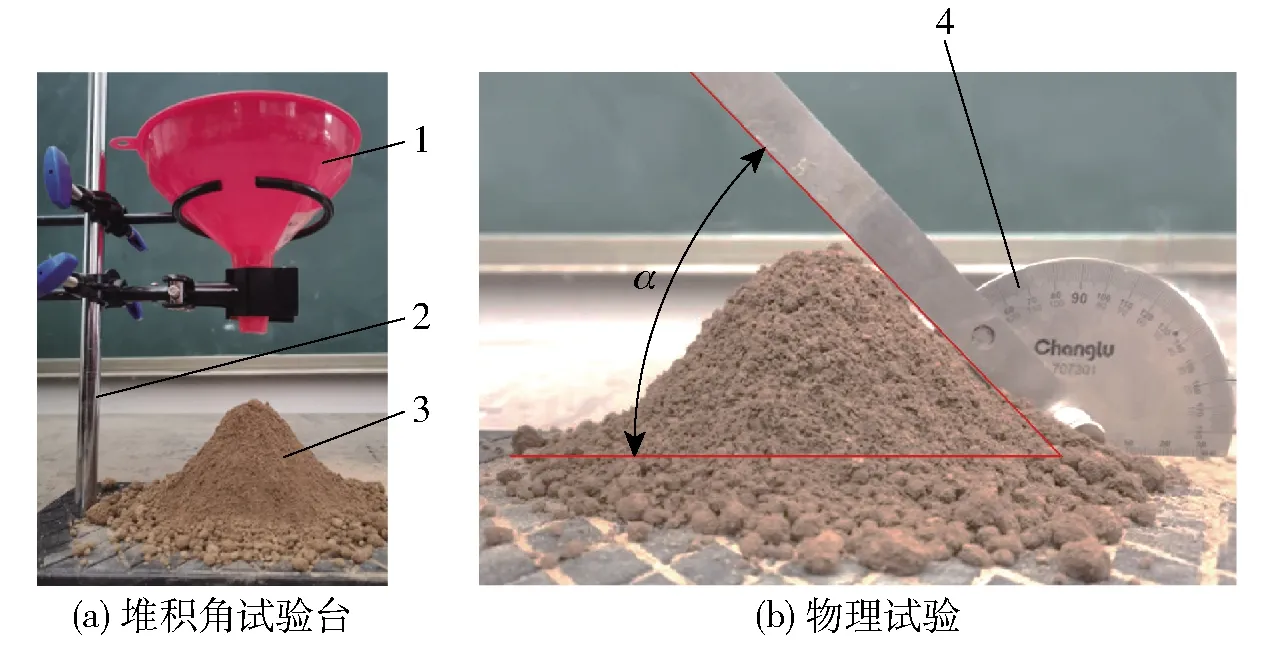
图2 土壤堆积角测定试验Fig.2 Determination test for soil repose angle1.漏斗 2.支架 3.土壤 4.量角器
1.2.3土壤堆积角仿真试验
参照文献[12]的方法,基于SolidWorks软件建立试验台的三维模型,如图3a所示,其几何尺寸与物理试验中漏斗的尺寸保持一致,仿真试验如图3b所示。
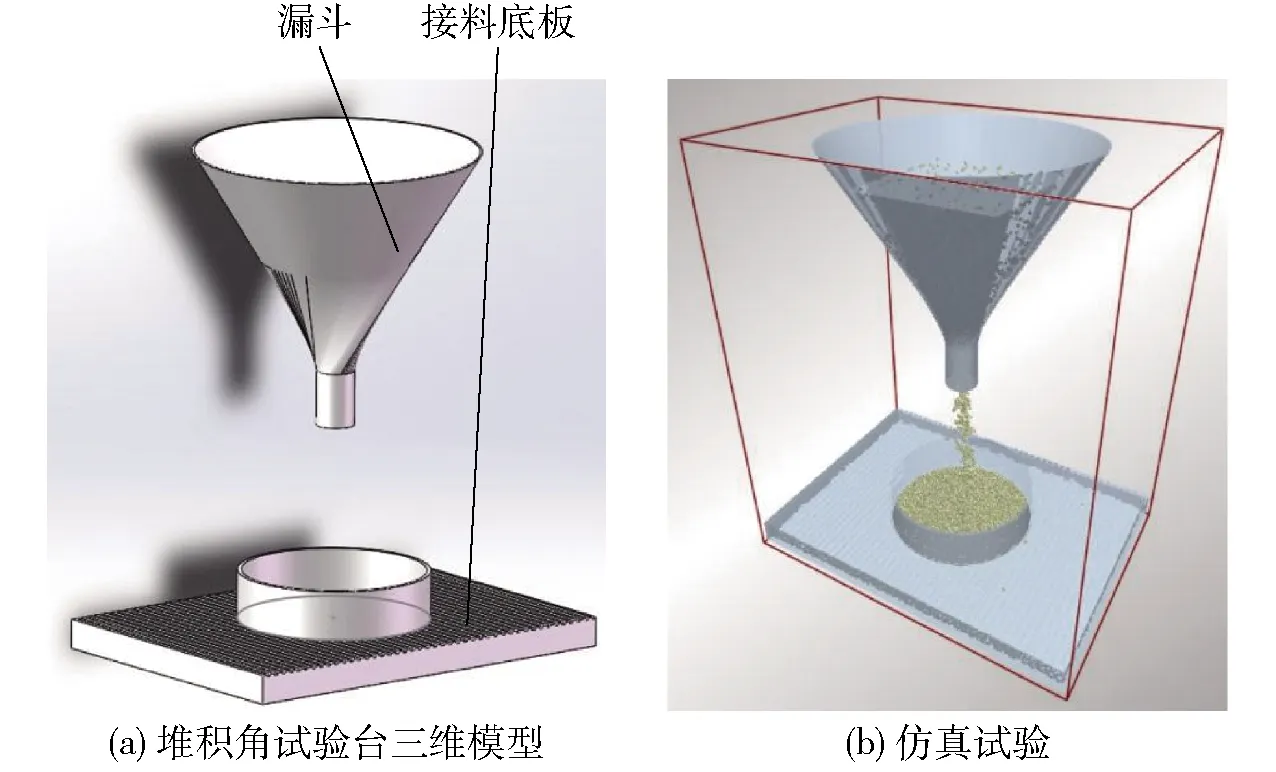
图3 土壤堆积角仿真试验Fig.3 Simulation test for soil repose angle
将仿真规模(小规模)、堆积角(43.25°)和材料堆积密度(1 210 kg/m3)等输入EDEM颗粒材料数据库(Generic EDEM material model database,GEMM)中,确定了需要标定的接触模型参数为JKR表面能4~12 J/m2、恢复系数0.15~0.75、静摩擦因数0.32~0.68、滚动摩擦因数0.01~0.05。
1.3 标定试验设计
基于上述土壤模型的参考值范围,以堆积角为试验评价指标,依据Design-Expert软件的Box-Behnken优化方法开展标定试验。试验因素编码如表1所示。
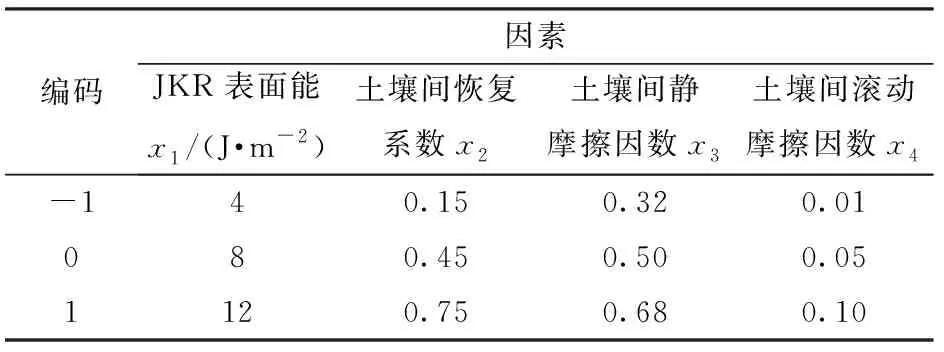
表1 土壤堆积角仿真试验因素编码Tab.1 Factors and codes of simulation test for soil repose angle
对同一接触参数下的堆积仿真试验重复3次,分别从生成土堆的2个不同方向截取图像,在CAD软件构建参考线并测量堆积角,结果如表2所示。
对上述试验结果开展方差分析,结果如表3所示,对试验结果开展多元回归分析得到堆积角回归模型为
(3)
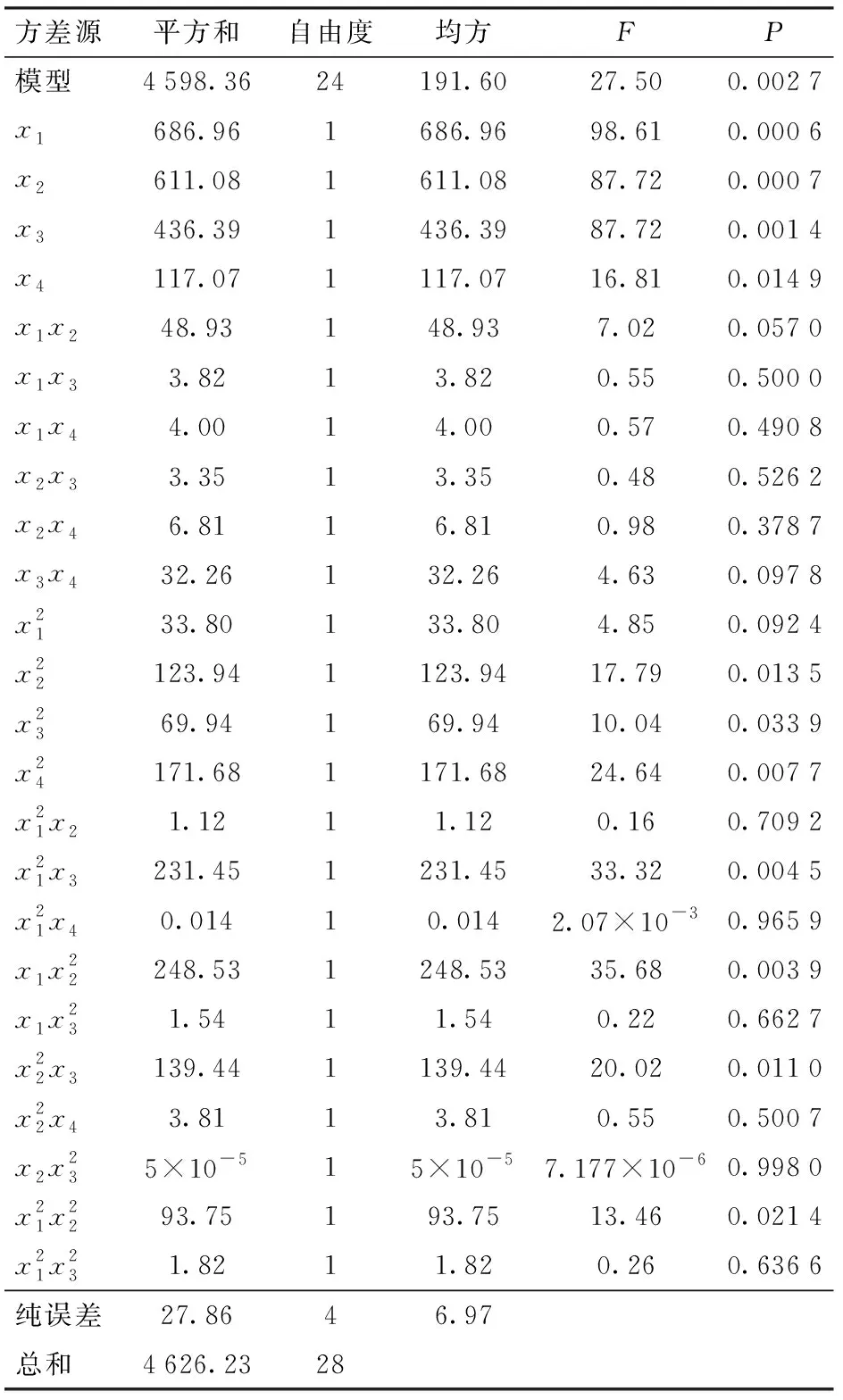
表3 回归模型的方差分析Tab.3 Variance analysis of regression model
根据Design-Expert软件中参数优化模块,以含水率13.4%±1%的土壤堆积角43.25°为目标对堆积角回归模型进行寻优,找到与堆积角实测值最接近的1组解,即土壤颗粒之间的JKR表面能9.04 J/m2,恢复系数0.15、静摩擦因数0.33、滚动摩擦因数0.05,该最优解下堆积角仿真值为41.59°,与实测值(43.25°)相对误差为3.8%。其中,仿真试验与物理试验如图4所示。

图4 土壤堆积角物理试验与仿真试验的堆形对比Fig.4 Stacked shape comparison between physical and simulation test of soil repose angle
2 土壤与旋耕刀材料接触模型参数标定
旋耕机触土部件旋耕刀常用材料为65Mn钢,本征参数[27]如表4所示。土壤与旋耕刀之间的接触模型选取Hertz-Mindlin (no slip),首先采用静摩擦试验、斜面试验和斜板碰撞试验分别获得土壤与65Mn钢之间静摩擦因数、滚动摩擦因数、碰撞恢复系数范围,最后采用土壤滑落试验标定上述3个参数。

表4 65Mn钢的本征参数Tab.4 Intrinsic parameters of 65Mn steel
2.1 静摩擦因数测定
搭建如图5所示的斜板试验台来进行静摩擦试验,其中,土块受力平衡方程为
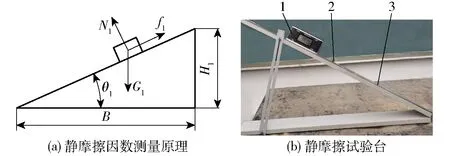
图5 静摩擦因数测量原理及试验台Fig.5 Static friction measuring principle and test bench1.倾角仪 2.试验土样 3.65Mn钢板
(4)
式中G1——土块重力,N
f1——土块所受摩擦力,N
N1——土块所受支持力,N
μ——静摩擦因数
θ1——斜面与水平面的夹角,(°)
将含水率为13.4%±1%、边长为1 cm土块水平放置于试验台的斜板上,缓慢抬升斜板改变其倾斜角,待测土壤样品开始滑落时记录此时的倾角,然后按式(4)计算静摩擦因数。共3个相同尺寸和含水率的立方体土块,每个土块做5次重复试验,最终得到土壤与65Mn钢的静摩擦因数为0.4~0.6。
2.2 滚动摩擦因数测定
通过斜板滚动试验来测定土壤与触土部件材料65Mn钢之间的滚动摩擦因数,搭建如图6所示的滚动摩擦试验台,斜板与水平板材料均为65Mn钢,宽度为100 mm,水平板水平放置,斜板倾斜一定的角度,与水平板连接处尽量光滑。将含水率13.4%±1%、半径5 mm的土球静置于高度为H2的斜板中间处,使土球自由滚动至停止,测量土球的水平滚动距离S,重复10次。
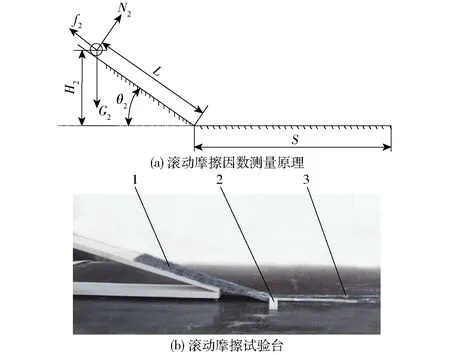
图6 滚动摩擦因数测量原理及试验台Fig.6 Measuring principle of dynamic friction coefficient and test bench1.65Mn钢板 2.刻度尺 3.土球
根据能量守恒定律,土球重力势能转换为摩擦能耗,计算式为
G2H2=μG2(Lcosθ2+S)
(5)
式中G2——土球重力,N
H2——土球初始高度,mm
L——土球在斜面上滚动的距离,mm
按照式(5)对滚动摩擦因数计算,得到土壤与65Mn钢间的滚动摩擦因数为0.04~0.2。
2.3 碰撞恢复系数测定
碰撞恢复系数是指碰撞后法向反弹速度与碰撞前法向前进速度的比值[3]。通过搭建碰撞试验台[28]来测定土壤与触土部件材料65Mn钢之间的碰撞恢复系数,试验原理及试验台如图7所示。将土球置于一定高度处使其作自由落体运动,当土球接触到65Mn钢板发生碰撞后做斜抛运动,经过时间t后落于底板上,其中碰撞时间t通过高速摄影系统来采集获取。

图7 碰撞恢复系数测量原理及试验系统Fig.7 Measuring principle and test system of collision restitution coefficient1.65Mn钢斜板 2.支架 3.65Mn钢平板 4.试验台 5.高速摄像机 6.显示器
碰撞恢复系数计算式为
(6)
其中
由于土球与65Mn钢板发生碰撞后作斜抛运动,故可得
式中Cr——土壤与65Mn钢间的碰撞恢复系数
vn0——土球与65Mn钢碰撞前的法向速度,m/s
从公式(5)、(6)、(7)看,此种赋存形态的孤石受力较为复杂,主要受孤石埋置的程度,坡面角度、孤石的埋藏边界,与周围土体的接触情况等影响。由图与公式可以看出,相比完全裸露孤石,部分埋入型重心更加深入土体中,在抗滑与抗倾覆上更加安全。但,此种孤石在长期的自然雨水的冲刷,会导致AC段埋深增大,而下面的OE段反而减小,造成OE受到很大的被动土压力,最终OE下方土体发生剪切破坏,导致孤石失稳滚落。由此可见,此种赋存形式的孤石不但要考虑孤石的稳定性,更要注意孤石周边土体的稳定性。
vn1——土球与65Mn钢碰撞后的法向速度,m/s
H3——土球落点至碰撞点间的竖直距离,mm
h1——土球初始位置至碰撞点间的距离,mm
S1——土球落点至碰撞点间的水平距离,mm
v0——土球自由落体至碰撞点速度,m/s
θ3——碰撞板倾斜角,(°)
vx——v1沿水平方向分速度,m/s
vy——v1沿垂直方向分速度,m/s
将含水率为13.4%±1%、半径为5 mm的试验土球在斜置钢板质心竖直方向高度为h1处做自由落体运动。当土球开始下落时,打开高速摄影系统拍摄,曝光量设置为100 ms,小球落至底板后,关闭高速摄影系统,记录土球从碰撞点落至接料板之间的时间t,并测量S1。对10个半径为5 mm的土球,每个土球做3次试验,得到碰撞恢复系数为0.04~0.6。
2.4 标定试验设计
以上述测定的3个参数作为试验因素,以土壤静滑动摩擦角为试验评价指标,进行仿真标定试验,因素编码如表5所示,试验结果如表6所示。
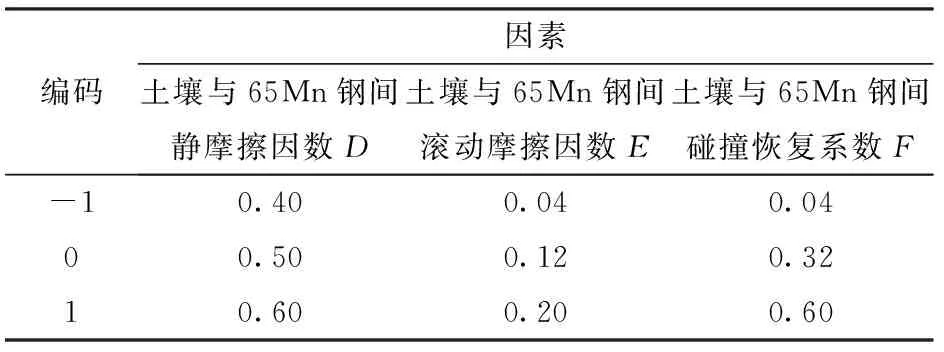
表5 土壤滑动仿真试验因素编码Tab.5 Factors and codes of soil sliding simulation test
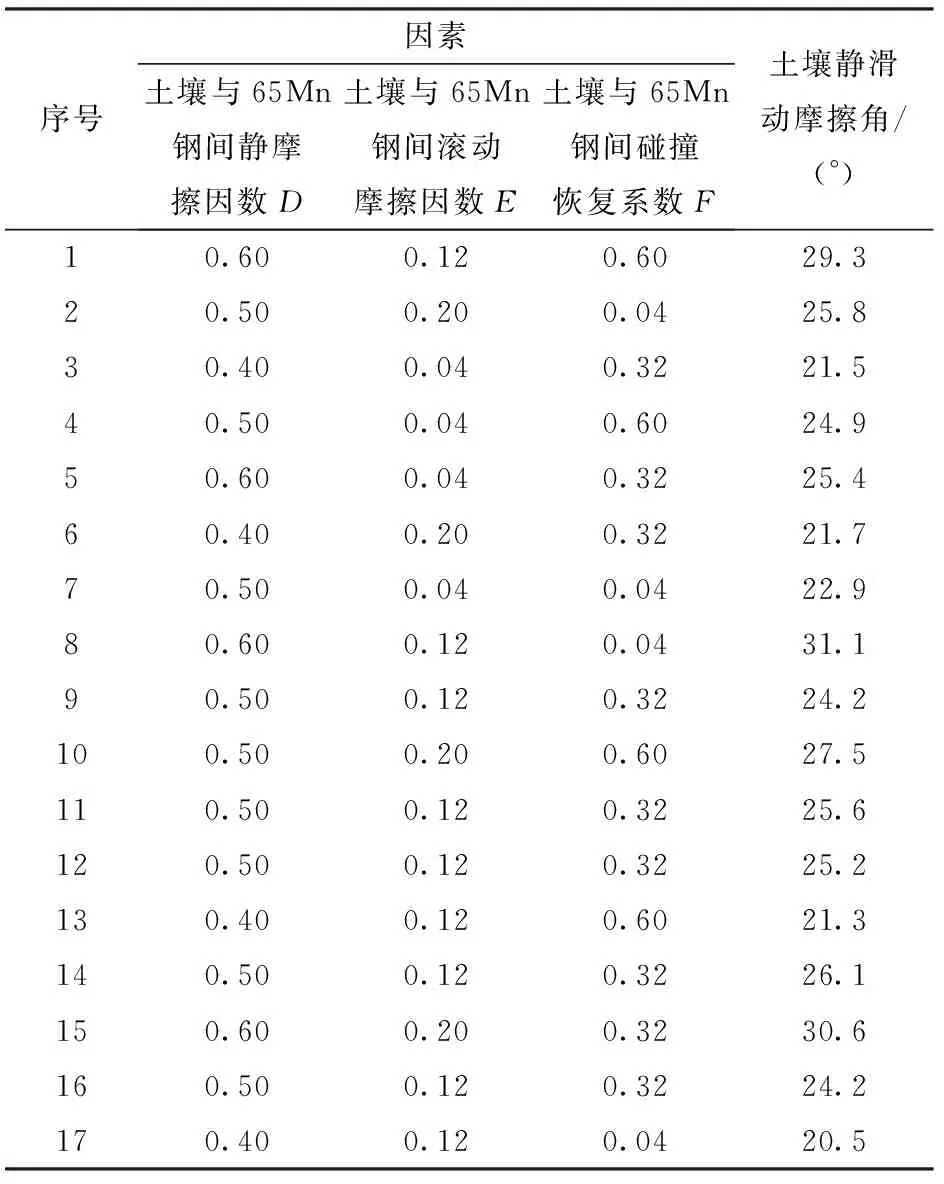
表6 土壤滑动仿真试验方案与结果Tab.6 Simulation test scheme and results of soil sliding
对仿真试验结果进行方差分析,如表7所示。多元回归分析得到静滑动摩擦角的回归模型为
y=25.06+4.65D+1.38E+0.93F+1.25DE-
0.65DF-0.075EF+0.007 5D2-0.27E2+
0.48F2-0.025D2E-1.18D2F-1.45DE2
(7)
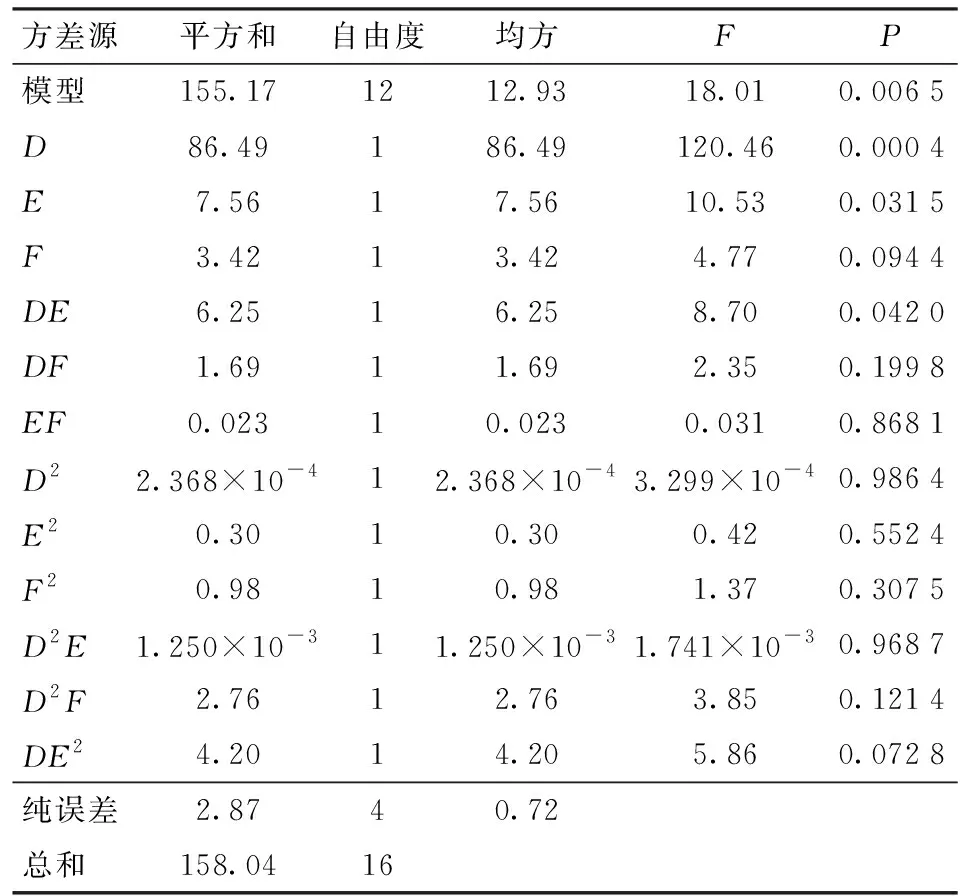
表7 静滑动摩擦角回归模型方差分析Tab.7 Variance analysis of static sliding friction angle regression model
通过Design-Expert软件中的参数优化模块,以土壤静滑动摩擦角23.6°为目标对建立的模型进行寻优,找到与实测试验最为接近的1组解,即土壤与65Mn钢板间的静摩擦因数0.50、滚动摩擦因数0.06、碰撞恢复系数0.18。其中,物理试验如图8所示,仿真试验如图9所示,该最优解下静滑动摩擦角仿真值为24.0°,与实测值(23.6°)的相对误差为1.7%,表明标定的参数准确可靠。

图8 静滑动摩擦角物理试验Fig.8 Physical test of static sliding friction angle1.65Mn钢土盒 2.400 g土壤 3.斜板 4.倾角仪
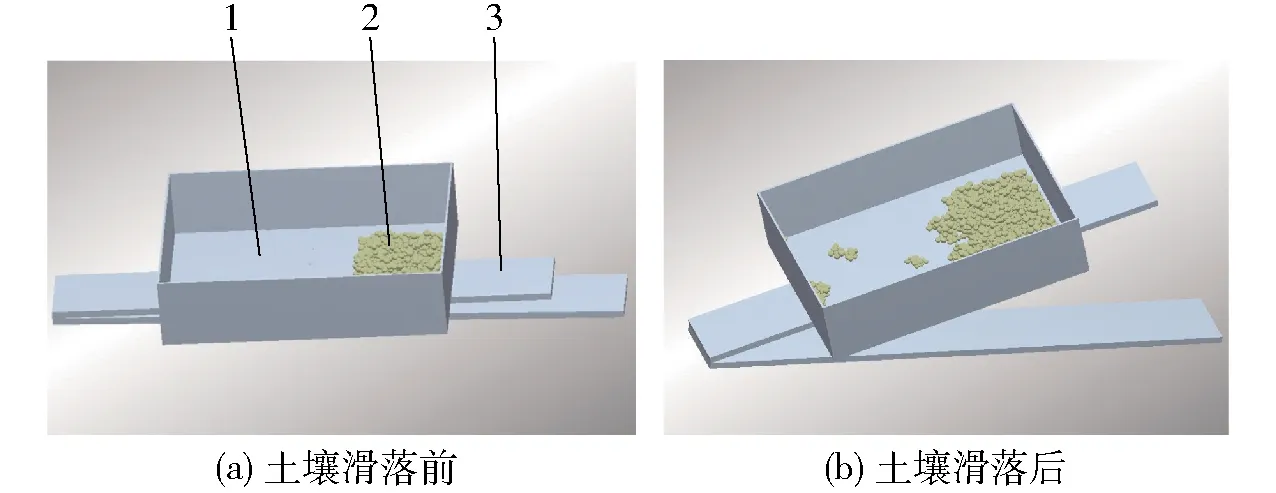
图9 静滑动摩擦角仿真试验Fig.9 Simulation test of static sliding friction angle1. 65Mn钢土盒 2.400 g土壤 3.斜板
3 坡地旋耕验证试验
3.1 试验目的
坡地旋耕作业时,土壤会在旋耕刀的扰动作用下发生位移,这种位移既可以反映土壤颗粒间的相互作用,还可以间接表征触土部件与土壤间的相互作用[29],因此,为进一步验证上述标定的所有参数的准确可靠性,基于本团队自主研发的山地履带拖拉机配套旋耕机进行坡地旋耕试验,以作业时土壤颗粒的位移[29-32]为响应值,将坡地实测试验的结果与EDEM软件中仿真结果进行对比。
3.2 坡地旋耕实地试验
3.2.1试验条件准备
试验在西北农林科技大学机械与电子工程学院专用试验坡地进行,首先在坡角15°±1°的坡地上经人工洒水、压实等工序塑造坡地土壤含水率、紧实度等参数,其中,用TZS-2X-G型土壤含水率速测仪(浙江托普云农公司生产)测定0~200 mm深度土壤含水率,范围为12.4%~14.4%,用TJSD-750-Ⅱ型土壤紧实度仪(浙江托普云农公司生产)测定土壤紧实度,范围为2~3 MPa。
3.2.2实地试验
实地试验中,参照文献[7]以铝块作为示踪器来追踪土壤颗粒位移。首先,在每个土壤示踪器(铝块)的表面用记号笔编写序号,按照图10a所示的埋设方案,将其布设在3种不同深度的土层中(表层0~50 mm、中层50~100 mm和深层100~150 mm各埋设45个示踪器,即图10a示意的3种颜色各有45个),并采用坐标测定架测量并记录此时每个示踪器的初始二维坐标;然后,基于山地履带拖拉机旋耕机组(设定旋耕刀轴转速200 r/min、作业速度1 km/h)完成旋耕作业,其中,山地履带拖拉机的车身姿态可以自动调整保证其始终保持水平,旋耕机姿态可以通过山地履带拖拉机上的坡地自适应悬挂系统实时调节,保证其与坡地面保持平行。最后,人工追踪所有带有编号的土壤示踪器,用坐标测定架测量并记录示踪器的最终二维坐标,对每个示踪器的最终二维坐标与初始二维坐标取差值,即得到示踪器沿着水平和侧向两个方向的位移。所有示踪器的水平位移、侧向位移分别取均值得到最终结果。
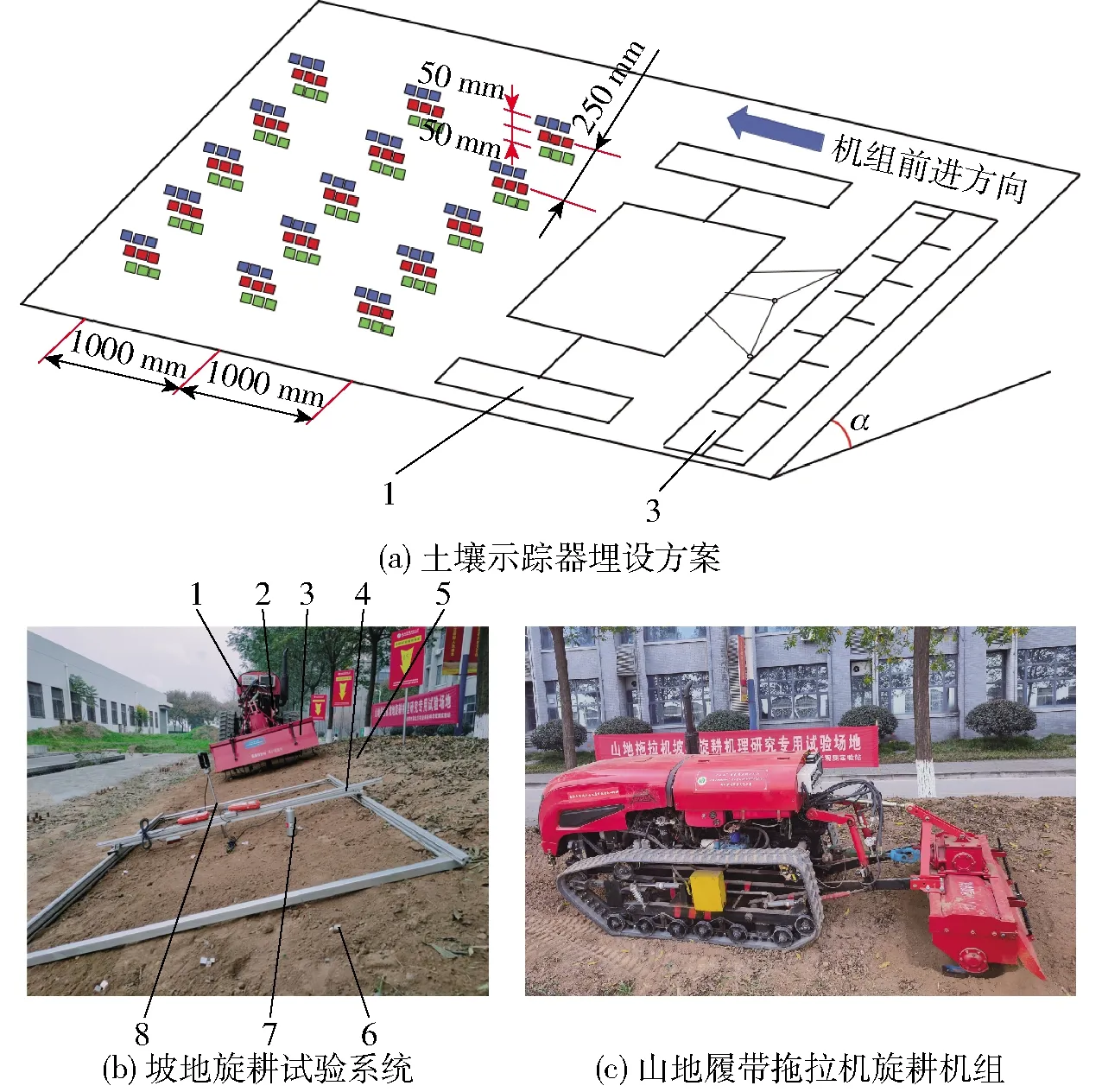
图10 坡地旋耕实地试验Fig.10 Field test of rotary tillage on slope1.山地履带拖拉机 2.坡地自适应悬挂系统 3.旋耕机 4.示踪器坐标测定架 5.坡地 6.土壤示踪器(铝块) 7.土壤含水率速测仪 8.土壤紧实度测定仪
3.3 坡地旋耕仿真试验
基于图11a所示的HandySCAN3D型扫描仪,对H245R、H245L旋耕刀进行三维结构扫描,经VXelements软件处理得到旋耕刀的STL点云模型,将STL文件导入逆向建模软件Geomagic Design X 64中得到旋耕刀三维模型(图11b),此方法得到的旋耕刀模型与实物具有极高锲合度,有效保证仿真的准确性。最后,将SolidWorks中建立的整个旋耕机三维模型导入仿真土槽模型,如图11c所示。
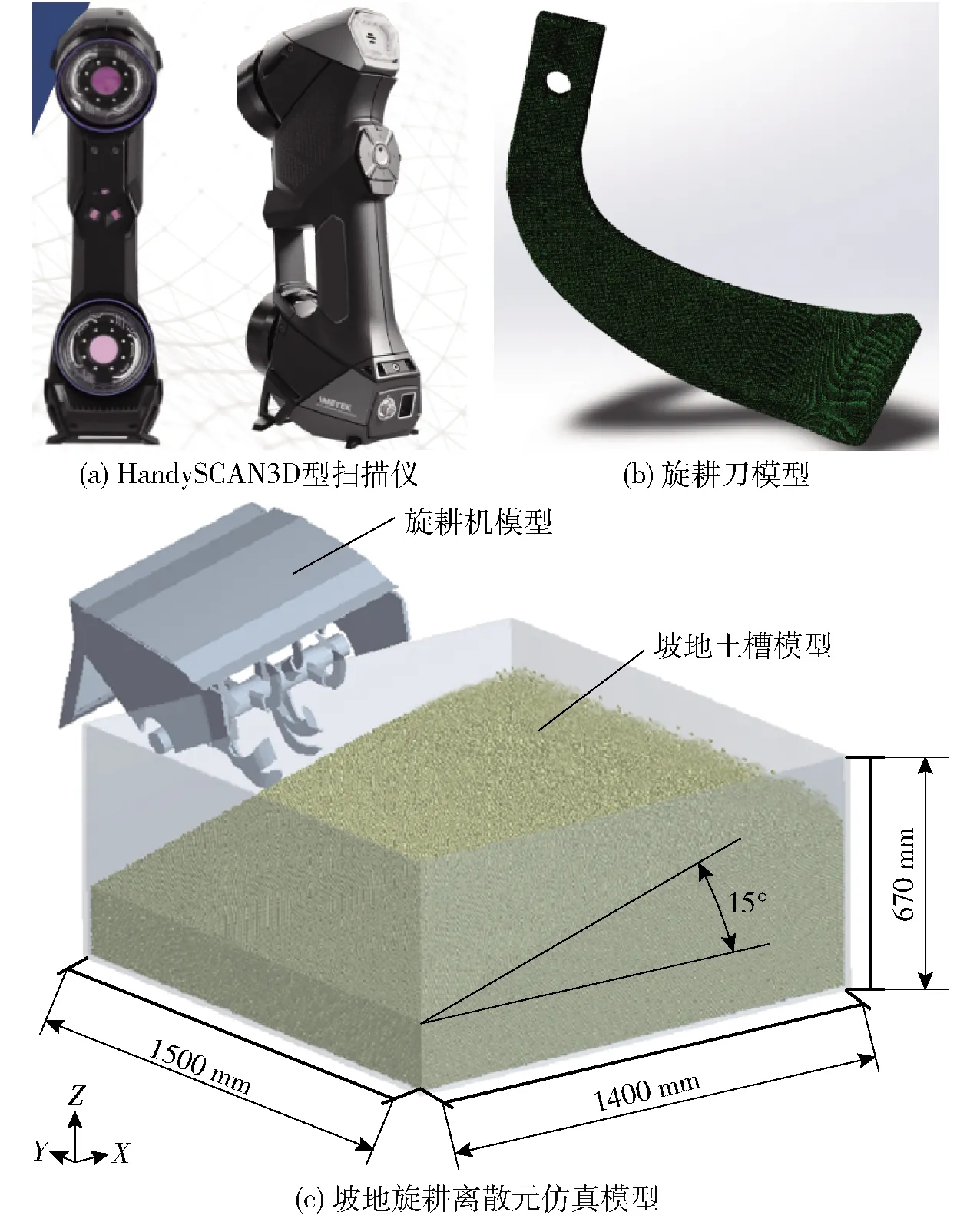
图11 离散元仿真模型的构建Fig.11 Construction of discrete element simulation model
依据实地试验条件,设定旋耕刀辊转速200 r/min,旋耕机作业前进速度1 km/h,入土深度设置为150 mm。在EDEM求解器模块对仿真时间步长、仿真时间及网格大小等进行设置。为保证仿真的连续性,设置其仿真时间步长为1.50×10-4s,仿真时间为5 s,网格单元尺寸设置为颗粒平均半径的3倍。仿真作业过程如图12所示。
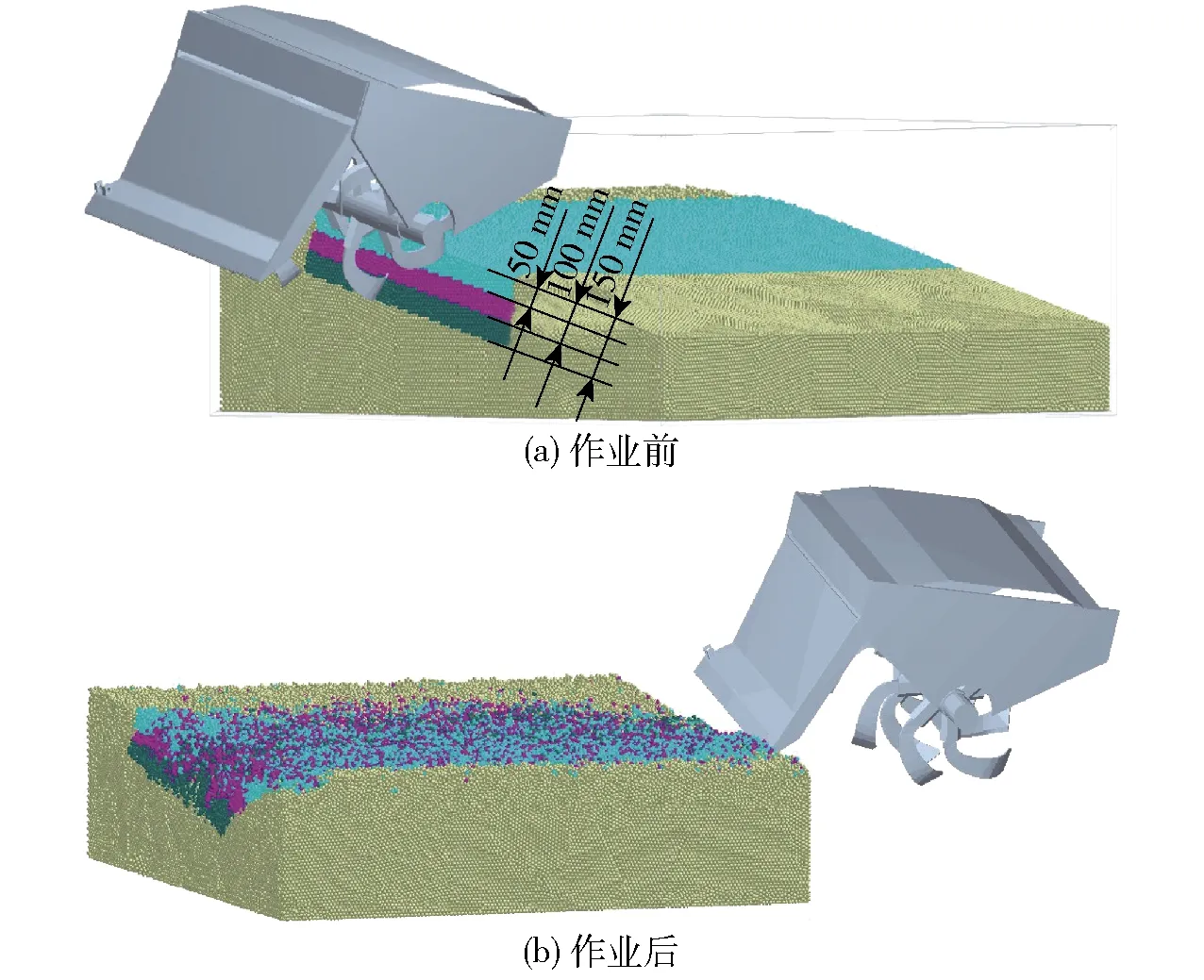
图12 坡地旋耕仿真试验Fig.12 Simulation test of rotary tillage on slope
基于Analyst模块进行后处理分析。在旋耕机幅宽范围内,垂直于坡面方向设置3个不同深度的土壤层,分别是浅层(0~50 mm范围的颗粒设置为蓝色)、中层(50~100 mm范围的颗粒设置为红色)和深层(100~150 mm范围的颗粒设置为绿色),如图12a所示。基于“Export Results Data”导出仿真前、后每种颜色的土壤颗粒在侧向(X轴方向)和水平方向(Y轴方向)上坐标的均值,对均值作差得到3种不同深度范围中土壤沿侧向和水平方向的位移。
3.4 试验结果与分析
实地试验中,根据旋耕前后土壤示踪器的坐标位置,计算每个深度范围内示踪器位移均值,可得浅层土壤位移明显大于中层和深层,原因在于深层土壤会受到浅层土壤重力的作用,其运动在一定程度上受到浅层土壤的阻碍。仿真试验得到同样的结论。并且,大部分土壤颗粒侧向位移的方向是由坡高侧指向坡低侧,说明坡角的引入增大了土壤颗粒侧向位移的程度,原因在于土壤抛撒过程中其自身重力沿着坡面向下的分力起到一定程度的作用。此外,无论土壤颗粒处于何种深度,在水平力的作用下,大部分土壤颗粒随着旋耕刀切土作用表现出向后运动的行为,并且土壤该运动所产生的水平位移大于侧向位移,表明旋耕刀的扰动对土壤沿着水平方向的重置程度大于侧向。土壤的这种水平位移在实际农业生产中是允许的,但是土壤的侧向位移会导致水土流失,因此,为了有效降低土壤颗粒的侧向位移(耕作侵蚀),需要在后续的工作中,更加深入地分析坡地旋耕侵蚀的机理,优化坡地专用旋耕机具。
为了验证所标定的离散元仿真模型参数的准确性,对坡地旋耕实地试验与仿真试验中3个不同深度中的土壤颗粒沿着水平方向和侧向平均位移进行比较(图13)。
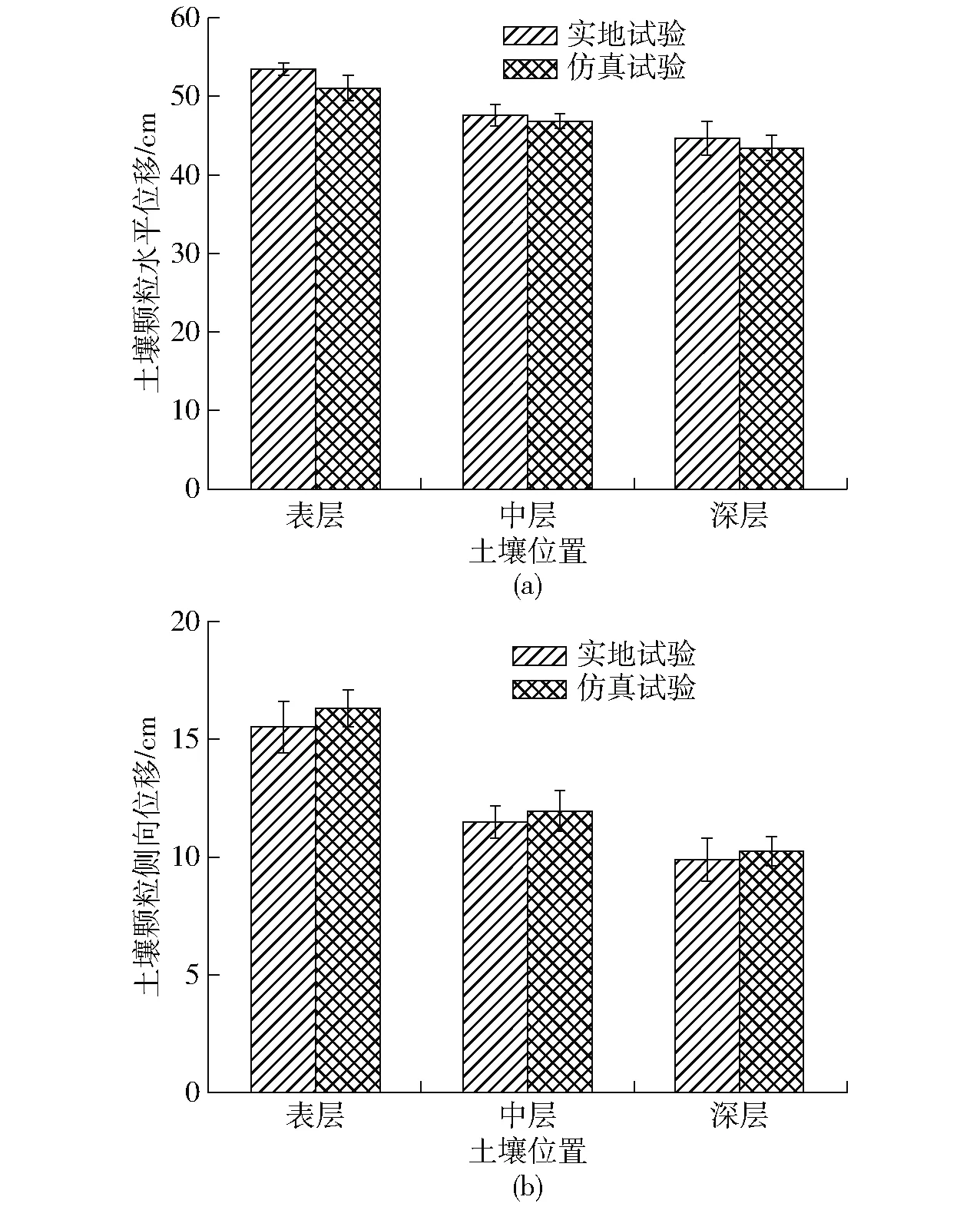
图13 不同位置土壤的运动位移Fig.13 Moving displacements of soil at different positions
依据图13a,定义仿真试验与实地试验结果的绝对差值与实地试验值的百分比为仿真相对误差[29],以此相对误差来表征离散元仿真参数标定的准确性。土壤颗粒水平位移相对误差为:表层土壤4.3%、中层土壤1.7%、深层土壤2.9%;由图13b可得,土壤颗粒侧向位移相对误差分别是:表层土壤5.1%、中层土壤4.3%、深层土壤4.0%。
综上,坡地旋耕实地试验与仿真试验相比,土壤颗粒的水平位移和侧向位移最大相对误差分别为4.3%和5.1%,表明仿真模型中标定的土壤参数与实际参数基本一致,验证了离散元仿真参数标定结果的准确性。
4 结论
(1)以土壤颗粒间的恢复系数、静摩擦因数、滚动摩擦因数及表面能参数为试验因素,以仿真堆积角为试验评价指标,依据Box-Behnken优化方法得到了堆积角回归模型,并经寻优得到了土壤颗粒间的恢复系数、静摩擦因数、滚动摩擦因数及表面能参数分别为0.15、0.33、0.05和9.04 J/m2,该最优解下堆积角仿真结果为41.59°,与物理试验相对误差为3.8%。
(2)以含水率为13.4%±1%的土壤为研究对象,经静摩擦试验、斜板试验、碰撞试验等获得了土壤与65Mn钢间的静摩擦因数、滚动摩擦因数、恢复系数的范围;以上述3个参数为试验因素,以土壤静滑动摩擦角为试验评价指标,依据Box-Behnken优化方法得到了静滑动摩擦角的回归模型,并经寻优得到了土壤颗粒与65Mn钢间的静摩擦因数、滚动摩擦因数及碰撞恢复系数分别为0.50、0.06和0.18,该最优解下的静滑动摩擦角仿真结果为24.0°,与物理试验的相对误差为1.7%。
(3)通过坡地旋耕实地试验和仿真试验对比分析,得到了土壤颗粒的水平位移和侧向位移的最大相对误差分别为4.3%和5.1%,处于可以接受的范围,表明标定的离散元仿真模型参数准确可靠。

