长江中下游崩岸预测方法研究

摘要：由于崩岸产生机理复杂，影响因素多样，导致准确预测崩岸十分困难。为了提高崩岸预测的准确性，分别提出了基于稳定岸坡角和模糊综合评价法的两种崩岸预测方法。前者基于土坡稳定原理，建立了充分考虑河床竖向冲深伴随着岸坡横向展宽这一动态机制的崩岸预测方法，该方法避免了当前绝大多数预测方法不能或没有考虑这一动态变化的缺陷，使得预测结果更加准确;后者在模糊数学隶属度理论基础上，将定性分析转变成定量评价，建立了不同水流动力条件和河床边界条件下的崩岸响应关系，该方法能够对崩岸进行预测的同时提供加固整治方案，在实际工程应用中取得了较好的效果。

关键词：崩岸预测; 模糊综合评价法; 稳定岸坡角; 长江中下游

中图法分类号：TV853 文献标志码：A DOI：10.15974/j.cnki.slsdkb.2022.02.001

文章编号：1006 - 0081（2022）02 - 0001 - 08

0 引 言

20世纪70年代以来，人们对崩岸预测方法进行了大量的研究。根据出发点和考虑因素的不同，已有研究成果可以分为河流动力学方法和土力学方法。前者主要有估计河岸崩塌宽度的河相关系式[1]、相对展宽度与河岸抗冲性指标和岸壁水流切应力之间的关系式[2]、河道展宽率与起动切应力和剩余切应力之间关系式[3-4]、基于水流能耗最小原理的极值假说[5-6]、河相关系式[7]、水流功率最小关系式[8]、输沙率最大关系式[9]和基于BP神经网络的河道崩岸预测模型[10]等;后者主要有相对河岸高度[11-12]、泥沙水下休止角[13-14]、临界挂空长度[15]、瑞典圆弧滑动法和bishop法[16-17]、临界淘刷宽度法[18]、临界高度法[19]和稳定坡比法[20-21]等。目前，河流动力学方法侧重理论分析和经验阐述，关注河段多年平均的宏观变化;土力学方法一般基于解析法，模型中包含了大量的参数，一方面难以测定参数，另一方面即使可以测定参数也因与实际情况存在较大差异，导致难以准确预测崩岸。因此，如何提高崩岸预测的准确性，阻止灾害的发生，减轻人民群众生命财产损失，是防洪减灾和河道治理领域迫切需要解决的课题，具有重大的理论和实践意义。鉴于此，本文分别提出了基于稳定岸坡角和模糊综合评价法的两种崩岸预测方法。

1 基于稳定岸坡角的崩岸预测方法

在水流动力作用下，可冲河床在竖向冲刷下切的同时，通常伴随着岸坡横向展宽这一动态过程。因此，在模拟河床竖向冲刷时，同时考虑岸坡的横向展宽对准确预测崩岸相当重要。但是现有的众多崩岸预测模型中，不能或没有考虑这一动态过程，导致预测结果与实际情况大相径庭[22]。针对该问题，根据长江中下游河道岸坡二元结构特征，笔者提出基于稳定岸坡角的崩岸预测模型。

1.1 基本假定

（1） 基于长江中下游岸坡具有上部黏性土、下部砂性土的典型二元结构特征，同时根据地质剖面图资料[23]，砂层顶板一般稍高于枯水位，假设枯水位为砂层顶板位置，水下稳定岸坡上界面取枯水位所在位置。

（2） 河床在竖向冲深过程中，岸坡坡脚区域砂性土由于侧向冲刷和河床冲深，砂土坍失发生横向展宽，假设砂性土水下稳定岸坡角为[α]，根据土坡稳定原理，竖向冲深[h]和横向展宽[w]之间存在着如下关系：[h=wtanα]。

（3） 伴随着岸坡坡脚冲刷进程，水下砂性土岸坡始终以水下稳定岸坡角[α]发生平行崩退。

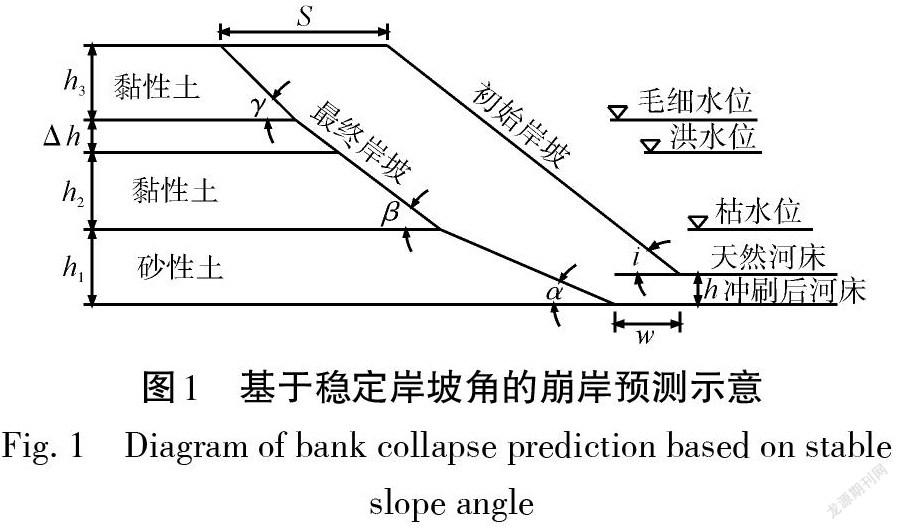
（4） 伴随着下部砂性土的平行崩退，在枯水位至毛细水位之间的黏性土水下稳定岸坡角为[β]，而毛细水位以上部分黏性土则以水上稳定岸坡角[γ]平行崩退（图1）。一般来说，对于长江中下游二元结构河岸大部分的“条崩”过程可分为3个阶段：① 近岸河床遭受冲刷，下部砂土岸坡变陡，上部黏性土悬空;② 挂空的上部黏性土层崩塌;③ 崩塌下来的土块被水流冲散并带走。本条假定下部砂土平行崩退时上部黏性土也发生平行崩退，似乎与河岸“条崩”机理不符，但实际上，上部黏性土发生崩塌后其断面近乎竖直，处于假性稳定状态，在河床冲刷处于相对稳定后，根据土坡稳定原理，最终的黏土岸坡必然呈现稳定岸坡角状态。

1.2 水上、水下稳定岸坡角

巖土材料水上、水下稳定岸坡角的确定有两种方法：① 工程地质调查法;② 综合计算法。

1.2.1 工程地质调查法

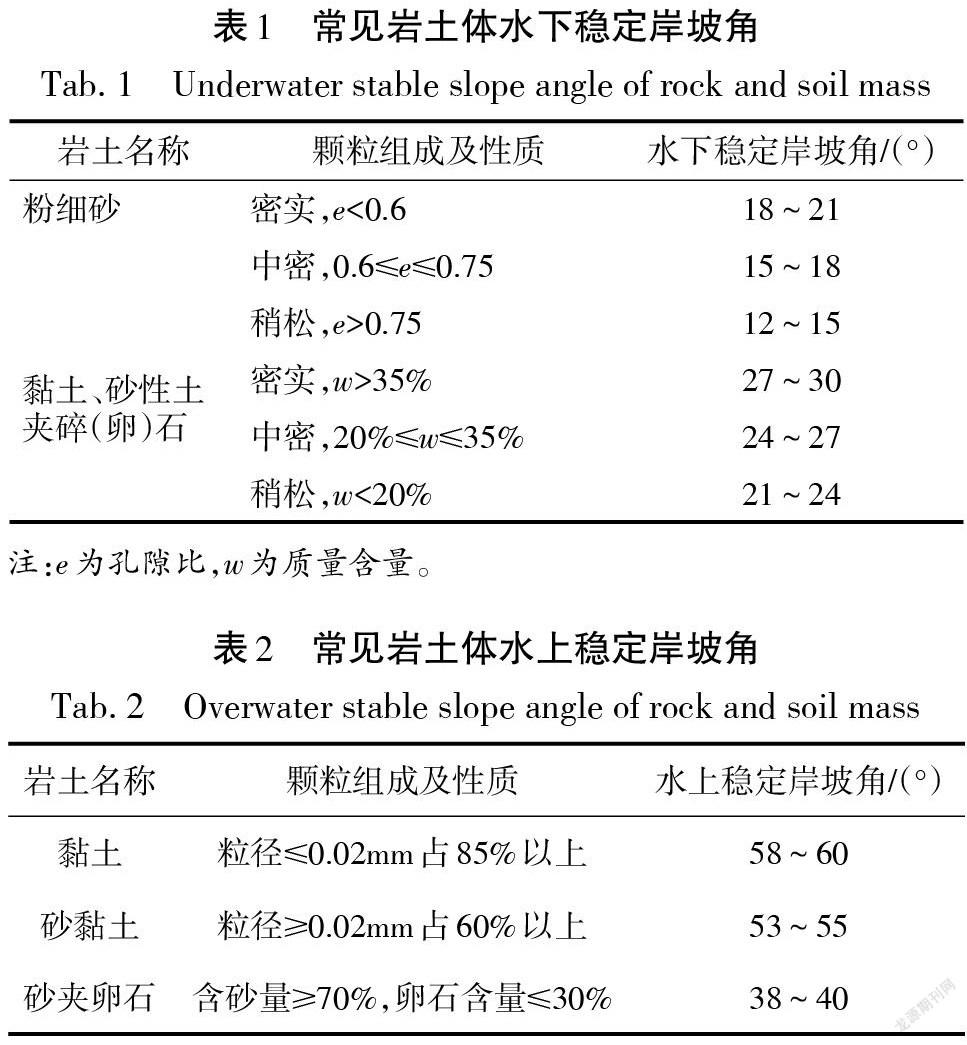
一般来说，不同岩土体组成的稳定岸坡角不同，细颗粒材料组成的稳定岸坡角比粗颗粒小，土层越密实，稳定岸坡角越大。根据地质调查法[24]确定的不同岩土体水下及水上稳定岸坡角见表1～2。

1.2.2 综合计算法

综合计算法是在地质调查法的基础上总结出来的，对于砂性土及碎石类土，水上、水下稳定岸坡角变化不大，一般均取稳定岸坡角为内摩擦角[φ];对于黏性土，则采用增大内摩擦角的方法来考虑土体黏聚力的影响，即综合内摩擦角[φ0]：

式中：当黏性土位于毛细水位以上时，[c]，[φ]采用天然快剪试验值，[γ]采用天然容重;当黏性土位于毛细水位以下时，[c]，[φ]采用饱和快剪试验值，[γ]采用饱和容重。[H]取毛细水位下或线上黏性土层厚度。

对于水下稳定岸坡角，地质调查法和综合计算法得到的结果基本一致;对于水上稳定岸坡角，由于地质调查法实测的数据多为极限稳定坡角，尚未达到最终稳定，其值一般大于自然稳定坡角，而采用综合计算法得到的值与自然稳定坡角较为接近，在实际操作中对于水上、水下稳定岸坡角的确定均可采用综合计算法。

1.3 毛细水上升高度

毛细水上升高度[Δh]与岸坡土体颗粒直径有关，粗颗粒毛细水上升高度小，细颗粒相应较高，经验取值见表3。为安全起见，分析中可取大值。

1.4 基于稳定岸坡角的崩岸预测模型

预测崩岸后最终岸坡由水下穩定岸坡和水上稳定岸坡的连线组成，水下稳定岸坡线由枯水位及水下稳定倾角[α]确定，水上稳定岸坡线由洪水位和毛细水上升高度[Δh]及水上稳定倾角[γ]确定，在枯水位和毛细水位之间，稳定岸坡角为[β]，根据图1可得坍岸宽度[S]和岸坡临界高度[Hcr]的表达式：

式中：[h]为坡脚处河床竖向冲深;[h2]为枯水位和洪水位之间变幅;其他符号见图1。

1.5 计算案例

长江宜昌一双层结构岸坡，初始高度17 m，初始岸坡比为1∶3.0，其中上部黏性土层厚12 m，下部砂性土层初始厚5 m。岩土体物理力学指标见表4。河段枯水位高程5.0 m（以初始河床高程为零点，下同），洪水位高程11.0 m。坡脚处河床竖向冲刷深度为6.0 m，且涨水过程中水位上涨速率和水下竖向冲刷速率均匀。毛细水上升高度取3.0 m。试计算岸坡临界高度[Hcr]和不同冲刷深度情况下的崩岸宽度[S]。

（1） 利用式（1）计算水上、水下稳定岸坡角，结果见表5。从表5可知，粉细砂水上、水下稳定岸坡角较为接近;黏土水上稳定岸坡角明显小于表2中所列数值，水下稳定岸坡角基本介于表1中所列范围。

（2） 根据式（2）和（3）计算岸坡临界高度[Hcr]和崩岸宽度[S]，结果见表5。

从表5可知：① 当岸坡初始高度为17.0 m时，崩岸宽度预测值为-15.8 m，说明此时岸坡是稳定的。② 当岸坡高度变为19.34 m时，崩岸宽度预测值为0，一方面说明此时岸坡处于临界稳定状态;另一方面说明此时岸坡高度已经接近临界高度[Hcr]，如果冲刷继续进行，岸坡将失稳。③ 随着竖向冲刷和横向展宽继续进行，岸坡不断向后崩退，在到达最大冲刷深度时，此时崩岸宽度为29.3 m，该值与实际崩岸宽度24.7 m基本接近。

2 基于模糊综合评价法的崩岸预测方法

影响崩岸的重要因素主要包括水流动力条件、河床边界条件和人类活动。所有的影响因素对崩岸发生与否均产生作用，但在不同的崩岸中各个影响因素所产生的作用和贡献度不同。目前很多崩岸预测方法依托少数几个影响因素在实际工程中积累的经验来对崩岸进行定量预测，由于考虑因素较为片面，其结果往往与实际情况相差很大[21]。为简单、快速、准确的预测崩岸，在全面考虑崩岸影响因素的基础上，根据模糊变换理论和最大隶属度理论，笔者提出基于模糊综合评价法的崩岸预测方法[25]，该方法在模糊数学中的隶属度理论基础上，将定性分析转变成定量评价，即利用模糊数学理论对涉及多种因素条件制约的目标做出总体的分析评价。

2.1 评价指标确定

为了对崩岸影响因素进行综合评价，评定各因素对崩岸的影响程度，以崩岸预测作为目标，列为第一层，即目标层。崩岸影响因素包括自然影响因素和人为影响因素两大类，这两个因素列为第二层，即影响层。第三层为指标层，共有15个。第四层为准则层（图2）。

影响崩岸的主要因素包括三大类，共计18个因子（表6）。对表6中影响崩岸的18个因子进行分析，将其归并为8个相对比较独立的评价指标，分别是造床值[Q2t]、河弯曲率半径与平均河宽比[rw]、岸坡组成、深泓离岸距离与平均河宽比、滩槽高差、岸坡平均坡角、岸坡内外水位差和岸坡防护。

2.1.1 造床值

水流造床作用与其输沙能力的大小及持续时间的长短有关。对于平原河流，一般近似地用流量[Q]的平方值与持续时间[t]的积[Q2t] （称为造床值）来反映水流造床作用。水流造床值的大小直接影响崩岸大小和强度，文献[26]针对长江下游大窝崩的发生特点，提出利用[ΣQ2t]来判别长江下游窝崩的发生。通过对长江大通站1980～1984年大于造床流量的各年日平均流量进行统计（表7），发现当[ΣQ2t<2×1011]时（[Q]>45 000 m3/s），窝崩发生较少;在[ΣQ2t>2.5×1011]后，窝崩发生较为频繁，上述研究表明：崩岸发生与造床值具有密切的关系。因此，可以通过对具体河段的造床值进行统计，找出崩岸发生频次与造床值的相互关系，可以为崩岸预测提供一定的判断依据。

2.1.2 河弯曲率半径与平均河宽比

加拿大学者Gerald，Nanson等 [27]通过研究大量蜿蜒性河段的迁移率，发现当曲率半径[r]与河宽[w]的比值[r/w<6]时河岸冲刷率会随着[rw]的降低而增加，当[r/w=2∼3]时达到最大值。美国学者Biedenharn等[28]研究了路易斯安那州雷德河上160个弯曲段的[rw]与河岸泥沙组成对冲刷率的影响，同样发现最大冲刷率发生在[r/w=2～3]。

2.1.3 岸坡组成

Torrey [29]研究了密西西比河下游岸坡稳定性与土体二元结构的关系，指出当下卧砂土层厚度[hs]与上覆黏土层厚度[hc]之比小于0.7时，岸坡处于稳定状态。实测地质资料表明[30]，长江下游彭泽马湖堤崩岸段和九江市城区防洪堤溃口处的[hshc]比值分别为1.49～1.00和1.67～0.77，说明这两段岸坡处于非稳定状态，这与Torrey的结论基本吻合。

2.1.4 深泓离岸距离与平均河宽比

通过长江中下游具有代表性的20段崩岸段的研究指出，崩岸段深泓离岸距离与平均河宽之比一般为0.07～0.30，一些强烈的崩岸段，深泓离岸距离与平均河宽之比小于0.1[31-32]。

2.1.5 滩槽高差

滩槽高差越大，越易发生崩岸。

2.1.6 岸坡平均坡角

长江中下游黏土、亚黏土与细砂土夹层河岸的稳定坡度均缓于1∶3.0。文献[20]指出长江中下游稳定坡比取值范围为1∶4.35～1∶2.22，随河型、地质不同而变化[31]。

2.1.7 岸坡內外水位差

长江中下游崩岸实例资料表明[30]，90%以上的崩岸发生在枯水期或汛后，尤其是大水年之后表现尤为明显。美国密西西比河下游大多数崩岸也发生在枯水期，同样证明了河道水位变化对岸坡稳定的影响。

2.1.8 岸坡防护

实测资料表明，当岸坡防护方量超过100 m3/m时，实际坡比可超过稳定坡比且岸坡较为稳定，因此可认为护岸防护方量大于100 m3/m时，即使坡比超过稳定坡比，河岸仍能维持稳定[20]。

根据上述研究成果，建立崩岸评价指标及模糊综合评价表（表8）。

2.2 崩岸风险评价

2.2.1 评价公式

崩岸风险根据模糊综合评价中集中隶属度最大值所对应的值确定，根据以下公式计算：

式中：B为崩岸风险的模糊综合评价集;K为评价指标的权重矩阵;R为评价指标的隶属矩阵;[ki]为第[i]个评价指标的权重，[i=1，2，3，…，8];[rij]为第[i]个评价指标对第[j]个稳定性的隶属度，若某个评价指标[i]隶属于某个稳定性[j]，则[rij]取1，否则取0;[bj]为第[j]个稳定性的隶属度，[b1]为稳定的隶属度，[b2]为基本稳定的隶属度，[b3]为欠稳定的隶属度，[b4]为不稳定的隶属度。

2.2.2 评价指标权重确定

评价指标权重是评价各指标重要程度的一个量化系数，本文做法是将每两个指标进行比较，按其对崩岸风险的重要性给0～4分，当两个指标同样重要时，各得2分;当其中一个比另一个重要时，则重要的得3分，相对不重要的得1分;当其中一个比另一个重要得多时，重要得多的得4分，不重要的得0分。各指标权重按下式计算：

式中：[ki]为第[i]个评价指标的权重，[i=1， 2， 3， … ，8];[mi]为第[i]个评价指标相对重要性得分和。表9为各评价指标权重的计算表。从表9中可知，岸坡平均坡角权重最大，造床值、岸坡组成、深泓离岸距离与平均河宽比以及滩槽高差并列第2，岸坡防护第3，岸坡内外水位差第4，河弯曲率半径与平均河宽比第5。

2.2.3 评价结果

通过计算，得出[B=b1，b2，b3，b4]，若[B]矩阵中稳定性隶属度最大值为[b1]，岸坡为稳定，不会发生崩岸;若[B]矩阵中稳定性隶属度最大值为[b2]，岸坡为基本稳定，崩岸风险较小;若[B]矩阵中稳定性隶属度最大值为[b3]，岸坡为欠稳定，崩岸风险较大;若[B]矩阵中稳定性隶属度最大值为[b4]，岸坡为不稳定，会发生崩岸。

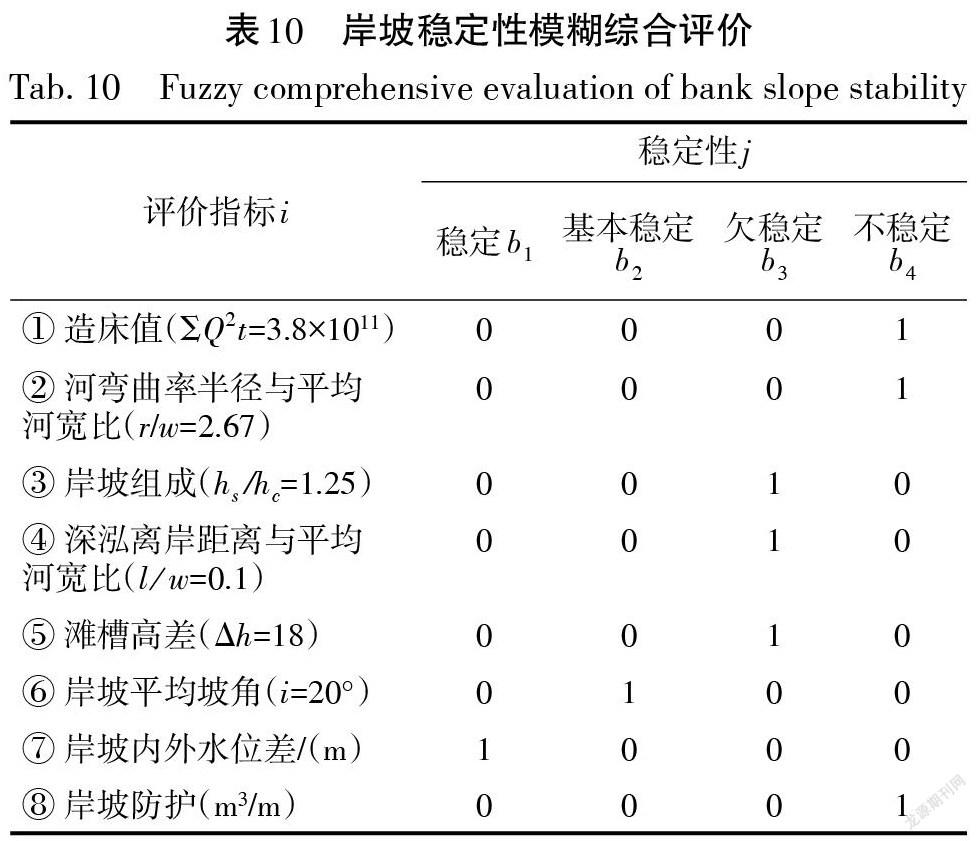
2.3 计算案例

南京下游一河段属于典型的弯曲河型，弯曲半径约3.2 km。2017年水文年截止当年10月底前造床值为[ΣQ2t]=3.8×1011。该河段一岸坡所处河道平均河宽约1.2 km，深泓离岸约120 m;滩槽高差为18 m，天然岸坡坡角约20°，岸坡属于典型的二元结构，其中上部粉土层厚8 m，下部粉细砂层厚10 m。河床床砂为粉细砂。岸坡未采取防护。岸坡内外水位差接近为0。根据岸坡特性，利用表8得到岸坡稳定性模糊综合评价表（表10）。b1=0.098;b2=0.152;b3=0.429;b4=0.322，可得B=（0.098，0.152，0.429，0.322），此矩阵中稳定性隶属度最大值为0.429，对应岸坡欠稳定，崩岸风险较大。考虑到该处岸坡尚未进行防护，可以考虑对岸坡进行抛石防护，防护方量按100 m3/m考虑，具体方案为将其坡脚河床填高3 m，同时现状边坡放缓至1∶3，则有b1=0.366;b2=0.143;b3=0.286;b4=0.206，可得B=（0.366，0.143，0.286，0.206），此矩阵中稳定性隶属度最大值为0.366，对应岸坡稳定，不存在崩岸风险。

3 结论与展望

针对崩岸预测这一难题，根据抽象问题简单化，技术问题具体化的思路，本文提出了基于稳定岸坡角和模糊综合评价法2种方法，为崩岸预测提供了新的技术手段和评价工具。

（1） 基于稳定岸坡角的崩岸预测方法，结合长江中下游岸坡二元土层结构特征，合理假设水下稳定岸坡上界面和砂层顶板位置为枯水位，使得预测模型较为接近工程实际;其次，预测模型考虑了坡脚处河床竖向冲深和岸坡横向展宽这一动态机制，对崩岸发生的诱因——河床竖向冲深及岸坡横向展宽——进行了完整的模拟，弥补了当前绝大多数预测模型不能或没有考虑这一动态变化过程的缺陷，使得预测结果更加准确;最后，预测模型将水下砂性土岸坡和水上黏性土岸坡按照各自的稳定岸坡角进行平行崩退，符合土坡稳定理论和实际情况，有可能预测的崩岸宽度较崩岸发生时的宽度要大，但岸坡最终达到稳定时的崩岸宽度应该与预测值较为接近，因为崩岸发生时一般尚未达到最终稳定，达到新的平衡尚需要一段时间，在这一段时间内岸坡还会进行调整，最终达到新的平衡。值得指出的是，基于稳定岸坡角的崩岸预测方法建立在长江中游常见的“条崩”特征基础上，因此，在使用时应该注意适用条件。

（2） 基于模糊综合评价法的崩岸预测方法较为全面地考虑了影响崩岸的18个因素，将其归并为8个相对比较独立的评价指标，根据模糊变换理论和最大隶属度理论，建立了不同水流动力条件和河床边界条件下崩岸的响应关系，能够简单、快速、准确地做出崩岸与否的评价。通过与实际工程的对比，预测结果与实际较为一致，说明运用模糊综合评价法预测崩岸是可行的。该方法能够在对崩岸进行预测的同时提出加固整治方案，具有较高的工程实用价值。特别是对长江下游常见的“窝崩”，由于当前利用定量的分析方法对窝崩发生与否做出预测还存在一些困难，因此，利用本文提出的模糊综合评价法不失为一种可行的方法。鉴于崩岸预测的复杂性，本文提出的评价指标及其权重的确定、评价标准的拟定均存在一定的人为性和局限性，需要加以持续改进，以进一步提高预测结果的准确性。

参考文献：

[1] 梁国亭，张仁. 黄河小北干流一维分组泥沙冲淤数学模型[J]. 人民黄河， 1996（9）： 37-39.

[2] 许炯心. 边界条件对水库下游河床演变的影响[J]. 地理研究，1983（4）： 60-71.

[3] 梁志勇，尹学良. 冲积河流河床横向变形的初步数学模拟[J]. 泥沙研究， 1991（4）： 76-81.

[4] 周建军，林秉南，王连祥，等. 平面二维泥沙数学模型的研究及其应用[J]. 水利学报，1993（11）：10-19.

[5] YANG C T，CHARLES C S. Theory of minimum rate of energy dissipation[J].  Journal of Hydraulic Divsion， ASCE，1979，105（7）：769-784.

[6] 张海燕. 河流演变工程学[M]. 北京： 科学出版社， 1990.

[7] 张红武， 江恩惠. 黄河高含沙洪水模型的相似律[M]. 郑州：河南科学技术出版社， 1994.

[8] CHANG H H. Minimum stream power and river channel patterns[J].  Journal of Hydrology， 1979， 41：303-327.

[9] MILLAR，QUICK .  Stable width and depth of gravel-bed rivers with cohesive banks[J]. Journal of Hydraulic Engineering，  1998，124（10）：1005-1013.

[10] 許全喜，谈广鸣，张小峰.  长江河道崩岸预测模型的研究与应用[J]. 武汉大学学报（工学版），2004，37（6）：9-12.

[11] OSMAN A M，THORNE C R. Riverbank stability analysis I： Theory[J].Journal of Hydraulic Engineering，ASCE，1988，114（2）：134-150.

[12] 夏军强，王光谦，吴保生.  平面二维河床纵向与横向变形数学模型[J]. 中国科学： E 辑，2004（34）： 165-174.

[13] IKEDA S，PARKER G，KIMURA Y.Stable width and depth of straight gravel rivers with heterogeneous bed materials[J]. Water Resources Research，1988，24（9） ： 713-722.

[14] PIZZUTO J E.Numerical simulation of gravel river widening[J]. Water Resource Research，1990，26（9）： 1971- 1980.

[15] FUKUOKA S.The mechanism of natural bank erosion process[J]. Water Resources and Hydropower Express，1996（2）：29-33.

[16] 余明辉，窦身堂. 河道崩岸机理研究[C]//湖北省水利学会. 纪念98 抗洪十周年学术研讨会论文集. 郑州： 黄河水利出版社，2008：43-52.

[17] 别必雄，徐卫亚，谢守益，等. 长江宜都河段茶店崩岸机理与防治研究[J]. 工程地质学报，2000，8（3） ： 272-276.

[18] 王延贵，匡尚富.  冲积河流典型结构岸滩落崩临界淘刷宽度的研究[J]. 水利学报，2014，45（7）：767-775.

[19] 王延贵，匡尚富. 河岸临界崩塌高度的研究[J]. 水利学报，2007，38（10）：1158-1165.

[20] 唐金武，邓金运，由星莹，等. 长江中下游河道崩岸预测方法[J].  四川大学学报（工程科学版），2012，44（1）：75-81.

[21] 彭良泉，周波. 长江中下游崩岸预测若干问题的探讨[J]. 水利水电快报，2017，38（11）：87-90.

[22] 彭良泉.  长江中下游崩岸防治关键技术研究及应用[M]. 武汉：长江出版社，2021.

[23] 中国科学院地理研究所， 长江水利水电科学研究院， 长江航道局规划设计研究所. 长江中下游河道特性及其演变[M] . 北京：科学出版社， 1985 .

[24] 彭良泉，齐美苗，胡静. 从一工程实例浅析水库水位变化对库岸的影响[J]. 岩石力学与工程学报，2001，20（A1）：922-926.

[25] 彭良泉.  基于模糊综合评价法的崩岸风险预测及应用[C]//中国水利学会. 中国水利学会2019学术年会论文集. 北京：中国水利学会，2019.

[26] 陈引川，彭海鹰. 长江下游大窝崩的发生及防护[C]//长江水利水电科学研究院. 长江中下游护岸工程论文集 . 武汉：长江水利水电科学研究院，1985：112.

[27] GERALD C，NANSON，EDWARD J，HICKIN . A statistical analysis of bank erosion and channel migration in Western Canada[J].Bulletin Geological Society of America，1986， 97 （8）：497-504 .

[28] BIEDENHARN D S， COMBS P G，  Hill GJ， et al. Relationship between channel migration and radius of curvature on the red river[C]// American Society of Civil Engineers.Proceedings of the International Symposium on Sediment Transport Modeling.New Orleans：American Society of Civil Engineers，1989.

[29] TORREY V H. Retrogressive failures in sand deposits of the Mississippi river， report 2， empirical evidence in support of the hypothesized failure mechanism and development of the levee safety， flow slide monitoring system[R] . Vicksburg： Department of The Army Waterway Experiment Station， Corps of Engineers， 1988.

[30] 张幸农，蒋传丰，陈长英，等. 江河崩岸的影响因素分析[J]. 河海大学学报（自然科学版），2009，37（1）：36-40.

[31] 段金曦，段文忠，朱矩蓉. 河岸崩塌与稳定分析[J]. 武汉大学学报（工学版），2004，37（6）：17-21.

[32] 彭良泉，胡昌顺，王罗斌. 对长江中下游崩岸治理设计的几点思考[C]//长江水利委员会. 长江崩岸治理与河整治技术交流会论文集. 武汉：长江水利委员会，2017：87-93.

（编辑：江 文）