基于改进逻辑方回归法的配电网长期负荷预测方法

刘秦娥，王晓东

（国网湖北省电力有限公司 襄阳供电公司，湖北 襄阳 441100）

0 引 言

在“双碳”背景下，加快构建一个安全稳定、主配协调的新型配电网，是现代电网发展的主趋势。配电网的负荷预测是整个电网规划分配的关键一环，直接影响一个地区的发电决策[1-4]。传统的负荷预测方法已经不能满足新型配电网的需求，传统方法常常将整个配电区域进行规划，求其整个区域的总负荷值，常用的方法往往是基于小数据、小样本的数学建模方法，如指数增长法、时间序列法等。随着智能算法的发展，现代预测方法包括支持向量机（Support Vector Machine，SVM）、长短期记忆神经网络（Long Short-Term Memory，LSTM）等人工智能深度学习算法。面对新型配电网的负荷预测既有理论意义，也是现在新型电网发展必要的一步[5-8]。

传统配电网规划的负荷预测方法增长率是根据经验人为给定的，已不适用现代配电网规划，因此本文提出一种基于改进逻辑方回归法的配电网负荷预测方法。

1 年负荷预测

1.1 饱和年负荷预测

空间负荷预测防范主要应用于地区负荷预测，该方法可以确定整个配电网系统的负荷分布情况，在时间上可以确定每个地区的负荷上限，即该区域电网的饱和值。本文的长期负荷预测设定为年负荷预测。

采用负荷密度法，其预测公式为

式中：P0为负荷饱和最大值；D为负荷密度系数；S为配电区域的面积；η为体积系数；φ为历史负荷同时率产生。

1.2 过度年负荷预测

新型配电系统区域一般都分为4个发展阶段，分别为初期、中期、后期以及饱和时期，由此逻辑回归算法非常适合上述场景。

1.3 改进逻辑回归算法

一般的经典逻辑回归算法在实现数据拟合的过程中考虑的方面比较少。该方法往往忽略了一些随机变量的影响，为此本文提出一种改进的逻辑回归算法。在该基础方法中引入一个惩罚系数C，该系数是一个随机变量，能够自适应调整模型的拟合效果，且提高了算法的收敛性。具体公式为

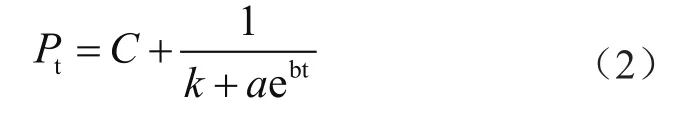
式中：Pt为配电区域负荷值；k、a、b均为模型的随机变量参数，且均为非负值。

上述方法无法计算配电区域的饱和预测情况，由此本文在其中又加入了饱和情况下的负荷值，公式为

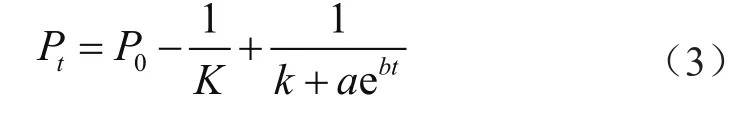
对式（3）分别求一阶导数和二阶导数得

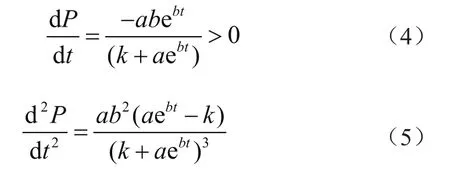
三阶导数为

(t1,P1)、(t2,P2)和(t3,P3)为配电区域负荷公式令其为0求得的3个零点，依次来划分区域。

根据上述3个零点即可划分为4个阶段，如图1所示。

图1 logistic 模型四阶段划分

2 基于粒子群改进的逻辑回归算法

粒子群算法通过不断迭代随机更新来寻找最优解。常规的逻辑回归方法其参数的选择往往是根据最小二乘法进行的，这样造成该模型参数不合适导致误差太大。寻优流程如图2所示。

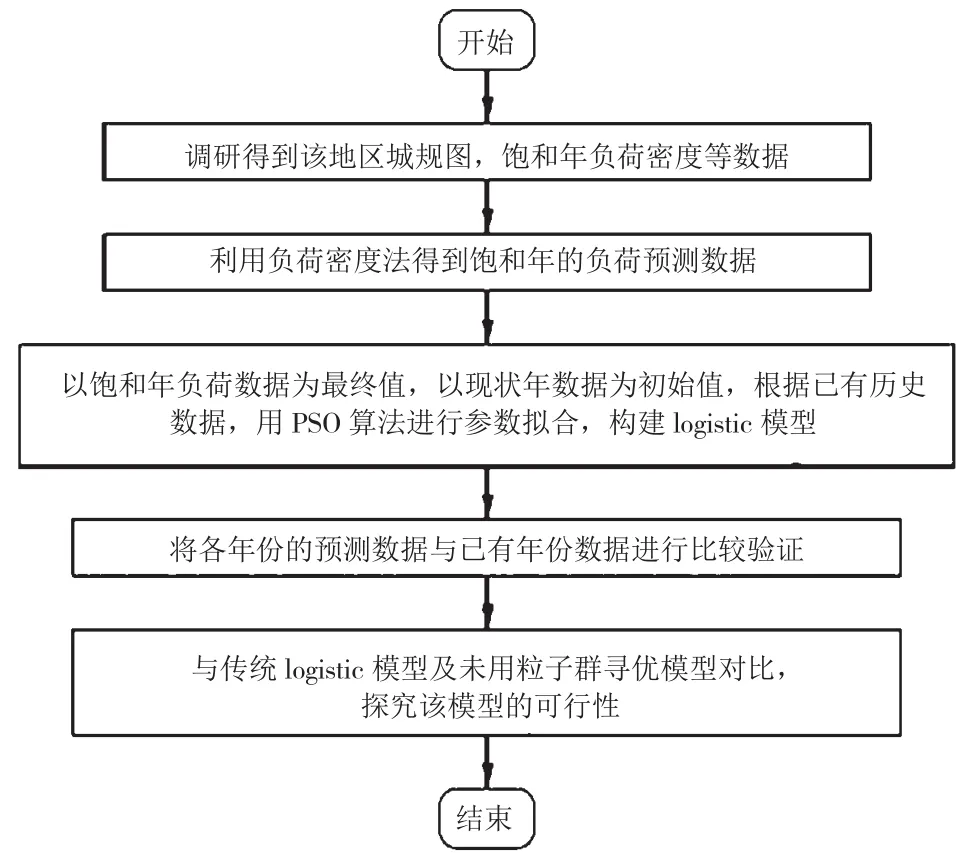
图2 寻优流程

首先获取输入部分，即配电区域的相关负荷数据。其次采用负荷密度法来预测饱和年的负荷情况。再次将上述数据作为输入，放入利用粒子群算法优化后的逻辑回归模型中。最终输出最后的预测值，并与没改进之前的算法进行结果对比。

3 仿真算例分析

本文以某地2001—2020年实际数据为例，证明所提算法的有效性。

3.1 饱和负荷预测

由式（1）可知，计算饱和负荷需要对其他数值进行调研，本文直接使用当地获得的数据，计算出饱和年负荷为1 506 MW。

3.2 过渡年负荷预测

当地实际负荷数据如表1所示。

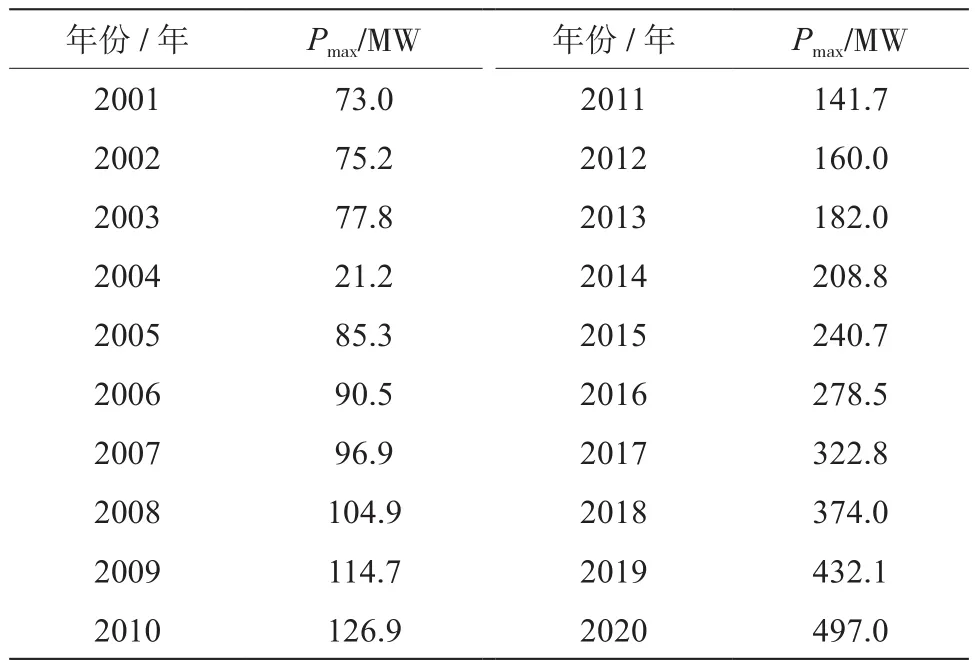
表1 历史负荷数据

预测结果示意如图3所示。

图3 预测结果

将式（2）、式（3）以及式（1）得到的结果作为初始参数，利用粒子群算法进行优化。本文中为了避免该算法过拟合，故而进行10次求解最优值，最终将10次结果的平均值作为模型的最后实际参数。

基于粒子群算法最终求出最优的平均值为k=7.062×10-4，a=7.973 5×105，b=7.6×10-3。

计算预测值与实际值的平均绝对误差为5.12%，相对误差绝对值的平均值为ε=7.22%，模型差异精度为α=(1-ε)×100%=92.78%。预测误差如图4所示。

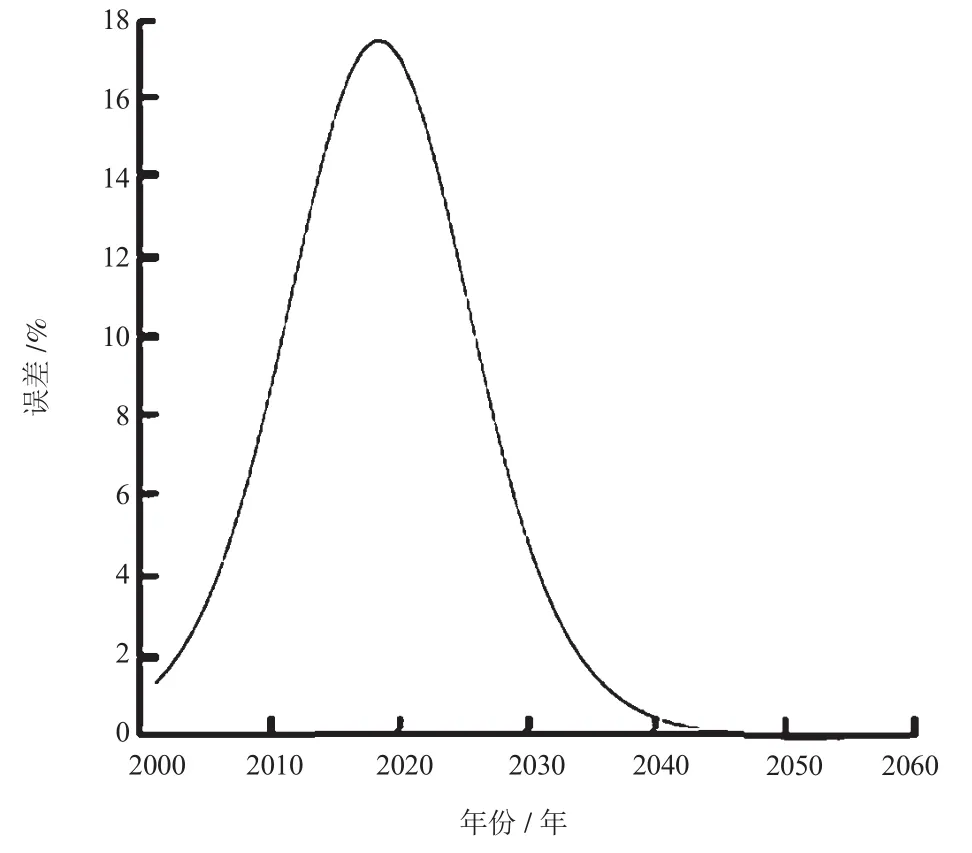
图4 预测误差

3.3 模型对比分析

各个模型对比如图5所示，从中可以看出本文提出的模型算法为最优，改进的逻辑回归算法比不进行改进的有明显提升。此外，采用粒子群算法的模型和不采用粒子群模型的结果也存在较大差异。上述结果均证明本文提出算法的优越性。

图5 各个模型对比

衡量预测效果的各个指标对比如表2所示。

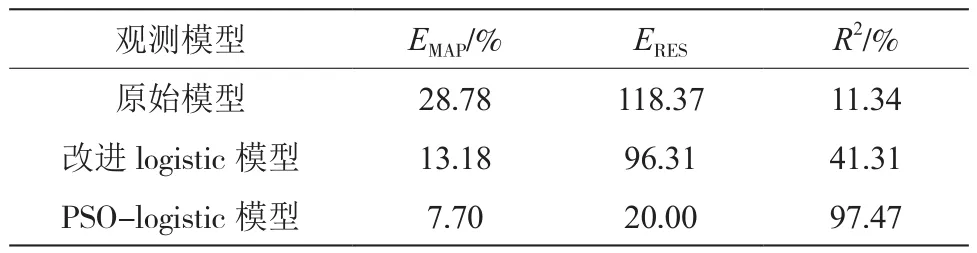
表2 各个指标与标准比值对比表

本文提出的算法在准确较高的情况下，模型的适用性也很高。

4 结 论

在“双碳”背景下，电网整体的规划离不开负荷预测。传统配电网的负荷预测主要以一些常规数学方法进行建模回归，该方法应用于新配电网中产生的误差会很大。针对新型配电网，本文提出一种改进的logistic方法来对新型的配电网进行负荷预测。首先进行空间负荷预测来适应新型配电网系统的负荷变化趋势，其次以上述步骤的结果作为饱和值，并利用粒子群算法对逻辑回归参数寻找最优值，以此来进行负荷预测，最后通过实际算例表明本文提出的改进算法的优越性。