基于路标重观测的月面巡视器激光雷达定位方法研究

李 硕，余 萌，曹 涛，郑 博，胡 涛

（1.南京航空航天大学 航天学院，南京 211106；2.上海航天控制技术研究所，上海 201109）

引 言

月球由于其独特的科学价值及丰富的潜在开发资源，已成为人类开展深空探测的首选目标，与地球相比，月面环境更加复杂且呈现非结构化的地貌表征，如月表崎岖不平、土壤松软、纹理贫瘠且月面光照条件不稳定，导致地面上成熟的导航定位算法无法简单移植到月球探测任务中[1]。因此，月面巡视器作为月表探测的科学仪器有效载体，需具备高可靠性、高精度的自主定位与地形研判能力[2]。

目前对于月面漫游巡视任务的研究大多聚焦于自主或半自主模式，定位与建图算法往往采用多传感器融合的方式，使用激光雷达、惯性测量单元（Inertial Measurement Unit，IMU）和相机融合定位与建图，但该方法受外界环境的影响较大[3]。在崎岖路段行驶时，随着时间的推移系统会累积较大的误差，状态估计的不确定性也会随着巡视器的前进而快速增长，降低了漫游巡视任务的可靠性与灵活性[4]。

针对月面环境巡视器定位难的问题，文献[5]提出了基于视觉惯性融合的组合导航算法，使用一种多层光流跟踪算法改进了视觉惯性里程计前端数据关联较大的问题；文献[6]提出了一种基于惯导/视觉/天文组合自主导航方法，采用集中自适应滤波算法提高了月面巡视器自主定位的精度。文献[7]提出了一种激光IMU紧耦合的旋转约束（Lidar Inertial Odometry and Mapping，LIO-Mapping）算法，将图优化方法应用其中，使用旋转约束方法将运动估计与全局地图对齐，但该方法处理速度较慢，尤其影响实时性。

为进一步提高巡视器定位与建图的精度，从点云地貌的显著性入手研究了一种基于历史路标重观测的月面巡视器主动导航方法，该方法旨在对历史路标的重新配准，进而实现巡视器位姿的历史估计值与当前观测值的融合更新，提高了定位与建图的精确性。该算法的整体流程如图1所示，首先在激光雷达（Lidar Odometry and Mapping，LOAM）算法与惯性测量单元预积分技术松耦合的基础上[8]，通过对点云的显著性研判来提取重观测的路标，并将激光雷达和IMU的状态估计误差作为重观测的触发条件，随后使用层次分析法进行备选路标的优先级排序，最终使用迭代最近点（Iterative Closest Point，ICP）算法进行点云配准来优化当前位姿。

图1 整体流程图Fig.1 Overall flow chart

1 重观测路标提取

考虑月面漫游巡视任务，在巡视器漫游过程中，大范围的点云显著性研判会占用星载计算机较多的计算资源，本文设计了一种缩减检索方法，每经过时间t就对当前帧点云进行显著性研判，并标注出显著值最高的点云地貌作为后续重观测的待匹配路标[7]，显著地貌提取的步骤如图2 所示。

图2 显著地貌标注Fig.2 Significant landform annotation

为提高显著性研判的可靠性与实时性，将当前帧点云均匀分成4块区域A、B、C、D，并求取每块区域的中心点Centre_A、Centre_B、Centre_C、Centre_D，以4个中心点为中心，用Range Search算法做范围搜索，逐步扩充点云直至每个集合包含足够数量的点云，使得这些点云能代表本区域的地貌。将4个点云集合标记为ContainerA、ContainerB、ContainerC、ContainerD，每个集合中的点云实时地进行SVD（Singular Value Decomposition）分解，得到3个特征值 β1，β2，β3，且令 β1＞ β2＞ β3，构建表达式为

当S小于阈值γ时，认为点云集合中有了足够数量的点，可停止范围搜索。在获得点云集合后，需要通过显著性研判来确定重观测的待匹配路标。采取基于协方差矩阵行列式的显著性评判方法：首先构建描述点云混乱程度的数量熵N和描述点云几何分布特征的函数g，再定义有关N和g的协方差矩阵行列式，通过行列式值的大小判断显著性。

1）构建数量熵为

使用激光LOAM算法提取每帧点云的边缘点和平面点，ni为边缘点的数量，p(ni)为数量直方图中边缘点数量的概率值。熵可描述一个系统的混乱程度，点云排列越是有序，熵值就越小；反之越是无序熵值就越大，因此数量熵的值越大，表明该处地貌的显著程度越高。将数量熵做归一化处理，即

2) 定义几何特性函数g

对一个点云集合中所有的点进行SVD分解，得到3个特征值λ1,λ2,λ3，且令λ1＞λ2＞λ3；

如果λ1≫λ2和λ3，则该点集呈线性结构；

如果λ1≃λ2≫λ3，则该点集呈平面结构；

定义几何特性函数g为

若函数接近0，则该点集近似为线性结构；若函数近似为1，则该点集近似为平面结构。

3) 定义函数f为

其中：f为2维特征向量。

定义协方差矩阵为

其中：n为点云的个数。

方差用来度量单维变量偏离均值的程度，协方差矩阵可以用来衡量特征向量和期望之间的偏离程度。协方差矩阵的行列式的值越大，表示特征空间中随机变量分布得越无序，与期望之间的偏离程度越大，反之该值越小，表示特征空间中随机变量分布得越有序，与期望之间的偏离程度越小[9]。行列式|Cr|的值越大，表示点集在几何、数量特征空间中的变化越显著，因此行列式|Cr|值的大小可以作为重观测路标的选取依据。找到最大|Cr|值对应的点云集合，将其作为重观测的备选路标。

2 重观测的触发机制

考虑星载计算机计算能力的限制与导航算法实时性要求，通过路标重观测频繁的更新自身位姿难以适合月面作业场景，需研究一种重观测的有效触发机制。主动导航重观测用来主动地降低系统状态估计的不确定性，因此重观测的触发机制要与状态估计的不确定性关联。本文设计了一种基于激光雷达与惯性测量单元状态估计误差差值的重观测触发方法：计算激光雷达及惯性测量单元的状态估计值误差差值的2-范数，若该值大于预定阈值 ζ，则认为当前的状态估计误差较大，需触发路标重观测，算法整体流程如图3所示。

图3 重观测触发机制Fig.3 Re-observation trigger mechanism

k时刻巡视器在全局系下的位置为

k～k+1时刻激光雷达测得的位姿变换矩阵，则k+1时刻激光雷达的位置估计为

惯性测量单元在k+1时刻测得的位置估计为

其中：Δt表示k和k+1时刻的时间间隔；表示加速度计的测量值；和分别表示加速度计的漂移和白噪声；k表示加速度计的测量值；和表示陀螺仪的漂移和白噪声；Rk和Rk+1分别表示k和k+1时刻从载体系到全局系的旋转矩阵[10]。

二者测量的状态估计误差差值为

其中：ρ为惯性测量单元和激光雷达的安装误差。

若Δδ＞σ，则认为当前惯性雷达位姿估计欠缺一致性，需要触发重观测。

3 路标优先级排序

在巡视器行进过程中实时存储4处路标，当新的路标被提取时，最早存储的路标将被释放。在触发重观测后巡视器将停止行进，综合显著性、距离、观测角度等因素，对4处备选路标进行优先级排序，选择一处最佳路标进行配准。

使用层次分析法对路标的优先级排序，该方法通过建立一种多层次的结构模型，定量地求出备选方案的权重系数，从而做出最优的决策[11]。

层次分析法的第1步是建立层次结构模型，在本方案设计中，共建立3层层次模型，分别是目标层、准则层和方案层[12]。目标层即选择重观测路标；准则层为影响路标选择的因素，包括显著值和距离；方案层为待匹配的路标。重观测的层次分析法结构模型如图4所示。

图4 重观测层次分析法结构图Fig.4 Structure diagram of re observation analytic hierarchy process

层次分析法的第2步首先构建成对比较矩阵，随后将影响因素两两进行对比，对比的结果作为成对比较矩阵的元素。

准则层相对于方案层的成对比较矩阵如表1所示，该成对比较矩阵的意义可以描述为显著值和距离相对于自身的重要性是1，显著值相对于距离的重要性是2。由于该成对比较矩阵只有两个指标，所以能通过一致性检验。

表1 准则层成对比较矩阵Table 1 Criterion layer pairwise comparison matrix

显著值和距离因素随着巡视器的行进不断改变，因此方案层相对于准则层的成对比较矩阵是动态变化的。本算法设计了一种基于商值的动态成对比较矩阵，如表2和表3所示。

表2 基于显著值的方案层成对比较矩阵Table 2 Scheme layer pairwise comparison matrix based on significance value

表3 基于距离的方案层成对比较矩阵Table 3 Pairwise comparison matrix of scheme layer based on distance

由于成对比较矩阵是正互反矩阵，以主对角线为对称轴，对应元素互为倒数，在确定矩阵（i,j）处的元素aij时，将不同路标i和路标j的显著值Li和Lj进行对比，若Li＞Lj，则把Li除以Lj得到的商值四舍五入取整记为aij；若Li＜Lj，则把Lj除以Li得到的商值四舍五入取整记为aji，则aij=1/aji。

通过后续实验验证得知，该方法得到的成对比较矩阵具有极高的一致性检验通过率。若当前成对比较矩阵未通过一致性检验，则本次重观测选取显著值最大的路标。最终汇总得到各路标权重矩阵如表4所示。表中b1i表示路标i对显著值的权重，b2i表示路标i对距离的权重。各路标权重系数为

表4 各路标权重Table 4 Weight of each road sign

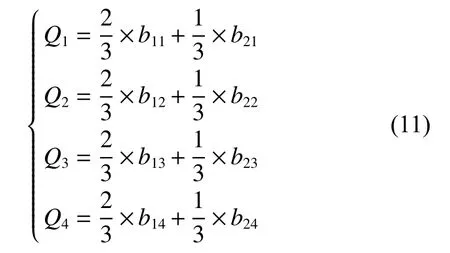
比较4个权重系数的大小，选取最大权重系数对应的区域作为重观测路标。

4 重观测配准

重观测的配准选用ICP算法，该算法是一种经典的点云匹配算法，用于估计两帧点云之间的位姿变换[13]。点云配准的表述式为

其中：R和t分别表示旋转矩阵和平移矩阵；Pt和PS分别表示目标点云和源点云。

ICP的一般流程为：获取巡视器的初始位姿（初始位姿对最终的配准结果影响较大）；迭代运行在PS中寻找点云Pt的匹配点，依据匹配结果，计算Pt、PS的位姿变换[13]。

在传统的 ICP 点云配准算法中，要将当前帧点云与地图整体点云进行匹配，但是进行大范围的点云检索不仅占用过多的星载计算机资源，也降低了配准的成功率，影响了可靠性与实时性[4]。因此在本算法中根据路标的距离范围在全局地图中进行对应的检索，并将当前的观测路标与地图中检索得到的点云进行精确配准，从而大大降低了计算量。

5 仿真验证

5.1 仿真实验条件

本文共设置2个仿真验证环节，分别是数学仿真以及月面模拟实地测试。在数学仿真中，选取3组模拟地景，对巡视器在月球表面的巡视场景仿真模拟，仿真的总时长350 s，巡视器上装配有激光雷达和惯性测量单元，激光雷达有效探测距离50 m，水平视场360°，垂直视场30°，根据模拟场景在软件环境内虚拟实时点云与惯性测量单元测量数据，其中对激光雷达和惯性测量单元的状态估计的高斯噪声也进行了模拟，噪声配置参数如表5所示。

表5 噪声参数配置表Table 5 Noise parameter configuration table

在半实物仿真测试中，使用一辆4轮移动单位，装载Velodyne激光雷达以及车规级惯性测量单元，测试本文算法场景如图5所示。实地场景共布置7处显著性地标，以供模拟巡视器（以下简称移动单位）进行点云重观测，移动单位执行定位建图功能，共行驶229.6 m，其中车载RTK（Real - Time Kinematic）提供位置解算的评测真值。

图5 实地场景测试Fig.5 Experimental setup

5.2 实验结果

为了验证本算法对不同地形的适用性，选用多种点云地貌重新进行仿真测试，地貌1、地貌2和地貌3的全局点云地图以及巡视器行驶轨迹如图6～8所示。

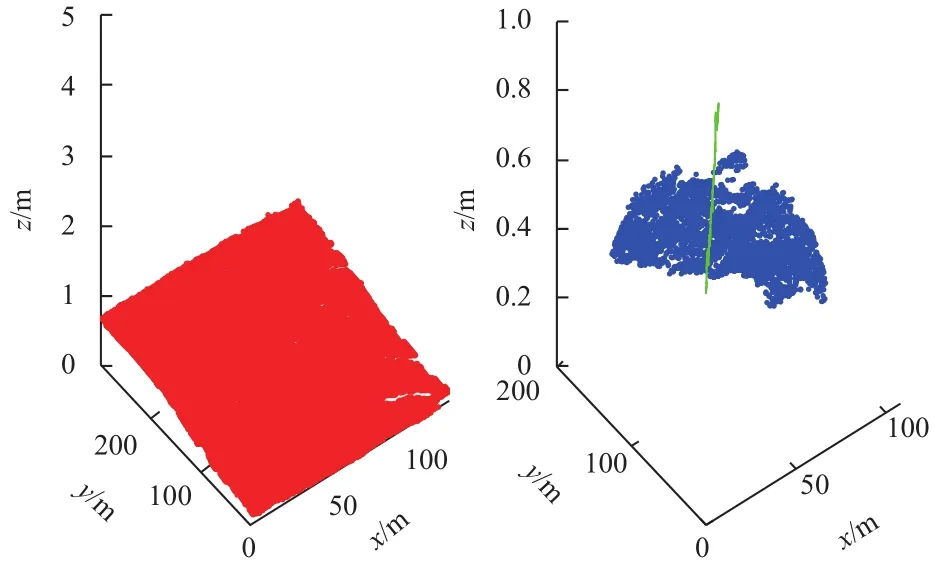
图6 地貌1点云地图与行驶路线Fig.6 Geomorphology 1 point cloud map and formal route

图7 地貌2点云地图与行驶路线Fig.7 Geomorphology 2 point cloud map and driving route

图8 地貌3点云地图与行驶路线Fig.8 Geomorphology 3 point cloud map and driving route

经过数次仿真测试，本算法取 γ=68，某一帧原始点云和提取到的显著地貌如图9所示。将激光雷达当前所采集到的点云均分成4块区域，每块区域用不同的颜色表示，在每个区域选取中心点并进行点云集合的扩充，获得的点云集合用黄色表示。随后进行点云地貌的显著性研判，并分别计算出每块区域的|Cr|值进行比较，将最大|Cr|值对应的区域标记为重观测的备选路标。

图9 原始点云与显著路标提取Fig.9 Extraction of original point cloud and prominent landmarks

在重观测触发环节中，选取触发阈值ζ =0.36，为了比较重观测触发机制的有效性，如图10所示，将地貌1环境下未使用重观测的误差曲线、每20 s定时启动重观测的误差曲线以及使用触发机制的重观测误差曲线进行对比。图10中黑色曲线表示单独使用IMU和轮速里程计的误差曲线，红色曲线表示定时启动的误差曲线，蓝色曲线表示使用触发机制的误差曲线。从图10可以看出，使用重观测方法大大降低了状态估计误差，提高了定位与建图的可靠性；而定时启动重观测的方法在一定程度上抑制了误差的增长，但与使用触发机制的效果相比，该方法抑制误差的效果较差。地貌2和地貌3对应的未使用重观测的误差曲线、每20 s定时启动重观测的误差曲线以及进行使用触发机制的重观测误差曲线对比图如图11和图12所示。

图10 地貌1环境下误差曲线对比图Fig.10 Comparison diagram of error curve under landform 1 environment

图11 地貌2环境下误差曲线对比图Fig.11 Comparison diagram of error curve under landform 2 environment

图12 地貌3环境下误差曲线对比图Fig.12 Comparison diagram of error curve under landform 3 environment

从图11和图12可以看出更换不同的地貌后，重观测方法依然能有效地控制误差，且使用触发机制的重观测方法抑制误差的效果依然优于定时启动的重观测方法，从而证明本算法的适用性、阈值的可靠性以及触发机制的有效性。

在外场测试中选择激光雷达LOAM算法[14]作为对比，控制移动单位在外场行驶20 min，以RTK的位置估计为真值对本文所提算法与LOAM算法进行比较，其中本文所提出的重观测触发、ICP重观测匹配算法在ROS平台下与LOAM算法进行集成封装，进程间的雷达定位、备选点云集合示例如图13所示。

图13 外场测试过程中的重观测点云选择示例Fig.13 Example of candidate point cloud re-observation and SLAM process

移动单位在行进过程中，RTK位置估计、基于Velodyne16线激光雷达下的标准LOAM算法，以及本文所提算法的定位结果如图14所示。

图14 RTK与基于Velodyne-16线激光雷达的两种算法里程估计Fig.14 Comparison between RTK and Velodyne-16 in terms of vehicle position estimation history

在实际测试中，本文所提算法根据当前位置估计状态、惯性测量单元估计状态进行重定位时机的研判，当有必要执行重定位时，在ROS环境下订阅LOAM算法的当前位置邻近点云（前后20 m），并从中运用点云显著性研判进行重观测点云集的筛选（见图13中左上部位示意），与当前观测点云集进行ICP匹配更新全局位置。所提算法与标准LOAM算法的三轴位置估计误差比较如图15所示（其中RTK收集的经纬高信息已进行坐标转换，并与定位建图初始位置映射对齐）。

本文所提算法在X、Y、Z轴的位置估计精度与与标准LOAM算法相比均有一定程度的提升，标准LOAM算法的最终定位误差为3.3 m或 1.4%R（3.3 m/229 m），这也与目前国际上公开的精度评测结果相近（加入惯性测量单元定位精度为1.2%R左右），相比而言，本文算法的最终定位误差为1.9 m或0.82%R，其中精度提升的主因为主动地选择显著性的路标进行点云重观测定位。

6 结 论

本文主要针对月面巡视器定位与建图精度问题进行研究，在计算机计算能力可控的范围内提出了一种月面复杂地貌下基于历史路标重观测的主动导航方法，并通过数字和实物仿真验证，本算法可有效降低状态估计的不确定性，并提高了定位与建图的准确性与可靠性。