泥石流容重的内涵诠释及其对灾害防治的启示
黄海,马东涛
1)中国地质科学院探矿工艺研究所, 成都, 611734;2)中国地质调查局地质灾害防治技术中心, 成都, 611734;3)中国科学院、水利部成都山地灾害与环境研究所, 成都, 610041
内容提要: 容重是描述泥石流性质的重要基础参数。本文基于泥石流运动过程的时空特征,厘定了最大容重、峰值容重和平均容重3个容重特征值。以蒋家沟1987年以来的泥石流观测数据为分析对象,分析了3个容重特征值在数值上的分布规律和影响因素。结果显示:①最大容重与峰值容重的关系式具有较好的相关性,最大容重与平均容重的关系式具有实际计算适宜性;②最大容重和峰值容重均与泥石流峰值流量呈正相关,与泥石流冲出规模关系不明显。在现有泥石流容重计算方法基础上,进一步界定了泥石流容重取样、计算和校验方法,构建了泥石流灾害特征值计算中容重独立取值原则,即峰值流量、流速、冲压力等计算建议选取最大容重,而一次冲出固体物质总量、堵河危险性和危险区范围等计算建议选取平均容重。研究结果可为泥石流灾害防治提供参考。
泥石流容重是描述泥石流物理性质最基本的参数,其定义为单位体积的流体重度 (李培基等,1982;章书成,1989)。容重不仅表达了流体性质差异,同时也是泥石流灾害的流速、流量、一次冲出固体物质总量和冲压力等动力特征值计算公式的重要参数,是泥石流灾害评价和治理中的关键参数之一 (陈宁生等,2003)。直接而准确的获取泥石流容重的唯一手段是在泥石流灾害暴发时现场取样测试,但这种方法有极大的限制性,在缺少长期观测的泥石流沟,观测到泥石流的发生的概率极低,即使是室内试验,由于流体的通透性差,目前也缺少先进技术对于容重进行有效测量。因此,如何精细刻画容重特征是泥石流灾害研究中一直悬而未决的问题。为了解决该难题,从20世纪60年代起,国内外的学者试图通过间接手段确定某一次灾害事件的容重来回避直接观测的缺陷,建立了基于泥石流的流态现象和物质特性来计算容重的方法 (Iverson, 1997;蒋树等,2012)。这些方法大体上可以归纳为3类:①从观测手段出发,通过配置最近泥石流事件的相似流体进行测试获取容重值的配方法和根据孕灾背景赋值的打分法 (国土资源部,2006);②基于泥石流堆积物组分的统计规律建立的颗粒分析法,也是目前学术界和工程界的主流方法,其中以杜榕桓等建立的方法应用较广泛 (杜榕桓等,1987;陈宁生等,2003,2010;余斌,2008,Li Yong et al.,2015);③基于泥石流容重的时空动态变化规律建立的预测估算法 (黄海等,2020a),如Huang Hai等建立的基于物源条件和水力条件建立的预测方法 (Huang Hai et al., 2020)。以上也可明显看到容重取值方法的逐步改良,主要体现在统计的方法上,从流态表观相似,提升到建立特征颗粒与容重之间的数量统计关系,或者孕灾背景与容重之间的统计关系,再进一步到颗粒粒度分布特征与容重之间的统计关系 (Wang Baoliang et al., 2018; Yang Taiqiang et al., 2019),直至近年来探讨的从时空变化角度分析容重的预测计算。但这些方法都似乎在回避两个问题,即计算所得的容重值的物理意义是什么,容重值具体刻画了一场泥石流的哪个断面、哪个时刻的性质,尤其是在泥石流调查中常用的现场浆体试验所测到的容重值(石建军等,2018),严重受制于被调访者的描述。现有计算方法中将容重作为一个笼统的概念进行研究的模糊处理方法,无法定时、定量的描述流体性质在时空尺度上的变化(李泳等,2009)。这种模糊的定义目前广泛应用于泥石流灾害的动力模拟(Kim et al., 2018)、风险评价(Ouyang Chaojun et al., 2019; Zou Qiang et al., 2020)、防治技术研究(张江华等,2015;Lee et al., 2019; Yuan Dong et al., 2019; Vagnon, 2020)等方面,这就使得我们无法判断分析结果的真实性,也是近10年来的新理论新方法难以在工程实践中广泛推广的重要原因。随着我国重大工程建设对地质敏感区的扰动越来越强烈,在叠加全球气候变暖的大背景下,对泥石流灾害的防灾减灾需求也与日俱增,铁路、水电等重大关键工程对于防灾减灾提出了更高的需求(Lu Chunfang et al., 2019;彭建兵等,2020)。本文针对泥石流灾害评价和治理中的关键特征值,定义了泥石流的3个容重特征值:最大容重、峰值容重和平均容重。结合蒋家沟泥石流观测站自1987年以来的连续观测资料,分析3个容重值的分布规律和影响因素,进一步优化了泥石流容重的确定方法,为泥石流灾害的防灾减灾提供重要的基础理论支撑。

图1 泥石流容重空间分布模型(基于蒋家沟泥石流观测)Fig. 1 Distribution model of debris flow density(based on the observation of the debris flow in Jiangjia gully)
1 泥石流容重特征值概念
泥石流容重是随着时空动态演化的,其值一般从最小1.30 g/cm3到最大2.40 g/cm3。时间尺度上,同一断面上不同泥石流运动时间点的容重是不断变化的,总体上具有“小—大—小”的趋势;空间尺度上,同一时刻,沿沟道不同断面的泥石流容重是不同的,一般来说形成区>流通区>堆积区,与沿程泥沙侵蚀规律密切相关(吕立群等,2017),同时在沟道横断面上呈现中间主流>两侧侧流(图1)。定量描述泥石流灾害特征时,泥石流的峰值流量和固体物质冲出总量是致灾规模的关键参数(Canovas et al., 2016)。灾害评估中,峰值流量决定泥石流冲出规模和泥石流灾害危害范围(Zou Qiang et al., 2017);灾害治理中,峰值流量决定拦砂坝结构受力、溢流口结构尺寸、排导工程截面尺寸等(Hu Hongsen et al., 2020),冲出固体物质量则决定拦挡工程规模(Liu Wei et al., 2020)。因此对于一次泥石流事件,峰值流量时的泥石流容重(峰值容重)、泥石流过程中出现的最大容重(最大容重)和整场泥石流事件的平均容重(平均容重)就成为连接流体物理性质和动力参数的关键链。
最大容重(γmax)代表了该次泥石流流体物质搬运能力上限,与泥石流形成的水土耦合过程以及床沙交换过程密切相关,受泥石流过程的复杂性(Liu Jingjing et al., 2009),其上限的形成机制和规律还不甚明确。峰值容重(γp)代表了此次泥石流物质输移的汇集过程和动力侵蚀能力,由于峰值流量的形成受沟道条件和泥石流运动过程的堵溃影响,其峰值流量时不一定达到流体最大携沙能力的饱和状态,因此峰值容重较最大容重可能略小。平均容重 (γm) 是描述整场泥石流事件的物质输移总量的数学统计概念,是由泥石流过程不同时间尺度进行加权计算所得的数学上的值,不代表全过程泥石流流体物理性质的描述。
2 研究方法和数据
2.1 研究数据
本文研究数据来源于的云南省昆明市东川区蒋家沟泥石流的观测数据(张军和熊刚,1997;康志成等,2006)。在搜集中国科学院东川泥石流观测站1987年以来的详细观测数据基础上,以规模较大、持续时间较长、无缺失观测为筛选原则,筛选出具有完整观测的187次泥石流事件。统计出每次泥石流事件的最大容重值与对应的流量极值、峰值容重与峰值流量、平均容重、一次冲出总量、一次固体物质总量、泥石流总历时等参数,同时确定最大容重出现时的阶段最大流量以及相应时间和峰值流量对应的时间。
2.2 研究方法
本文主要通过分析蒋家沟观测数据,探索三个泥石流容重特征的时序特征、统计关系以及与灾害动力特征之间的相关性,并提出泥石流勘查设计中容重的取样、计算方法及计算结果检验方法,进而提出防灾工作中对泥石流容重特征值的取值建议。
(1) 时序分析方法。为了分析某一次泥石流事件中最大容重和峰值容重出现的时间,确定最大容重值对应的流量极值时间点距离泥石流暴发时间点的时长(Tγ)和峰值流量时间点距离泥石流暴发时间点的时长(TQ)。计算Tγ和TQ的时序特征Δ,计算公式如式(1)。

(1)
式中:Tγ为最大容重时的流量极值距离泥石流龙头时长,s;TQ为峰值容重时距离泥石流龙头时长,s;T为泥石流总历时,s。
(2) 泥石流水文过程特征值计算方法。引入泥石流水文过程特征值κ描述一次泥石流事件的汇流过程,参数定义为峰值流量与平均流量之比,计算公式如式(2):
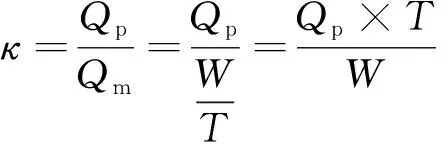
(2)
式中:Qp为泥石流峰值流量,单位m3/s;Qm为泥石流平均流量,m3/s,W为泥石流一次冲出总量,m3;T为泥石流总历时,s。
(3) 泥沙系数计算方法。泥沙系数(φ)主要用于根据清水流量计算泥石流峰值流量,是泥石流规模的放大系数主要部分之一,泥沙系数利用公式(3)计算(国土资源部,2006):
(3)
式中:γc为泥石流容重值,g/cm3;γw为清水容重值,g/cm3,本文取1.0 g/cm3;γs为泥石流中岩石容重值,g/cm3,本文取2.65 g/cm3。
(4) 一次固体物质冲出量计算方法。一次固体物质冲出总量按照式(4)计算(国土资源部,2006):
(4)
式中:Ws为泥石流一次冲出固体物质总量,m3;其他参数同前。
3 结果分析
3.1 容重值的时序特征
在泥石流运动过程中,最大容重和峰值容重可能是同时出现,也可能不同时出现。泥石流运动过程中液相物质和固相物质收到边界条件的约束机制是不同的(舒安平等,2010,2016),从而导致两者在泥石流过程中的动力特征有差异,主要有浆体与颗粒之间的速度差异、不同粒径岩土体搬运速度差异,从而导致泥石流运动过程的液相与固相的汇聚速度不一致,体现在容重参数上,就是观测中表现的最大容重与峰值容重的时序差。蒋家沟1984年以来的187次泥石流灾害中,最大容重与峰值容重相等的次数约占57.75%,最大容重与峰值容重时差小于总历时0.25的占33.69%,最大容重与峰值容重时差小于总历时0.75的占100%(表1)。

表1 最大容重与峰值容重时序特征Table 1 The time sequence characteristics of the max-density and the peak-density

图2 容重时序特征与流量特征关系Fig. 2 The relationship between the discharge and the time sequence of density
时序特征值Δ与水文过程特征值κ基本分布形态呈三角形(图2)。当水文特征值κ≥225时,最大容重与峰值容重具有同步特性。随着κ值变小,时序特征值分布幅度越宽,分布范围最宽为[-0.75,0.75],即最大容重与峰值容重的时差最大不超过泥石流总历时的75%。一般来说峰值流量与最大容重对应的最大流量之间的过程是泥石流最主要的物质搬运阶段(王洋等,2017),时序特征值越小则泥沙输移越集中,而流量特征值越大则流量过程线的尖峰形状越明显,故三角形分布特征完好的描述了泥石流泥沙输移过程的演化趋势。
3.2 容重特征值的相互关系
3个容重特征值的数值分布规律是计算中选用的重要依据。蒋家沟泥石流观测数据显示,1987年以来暴发的泥石流最大容重值基本在2.0 g/cm3以上,且最大容重、峰值容重和平均容重之间具有一致的变化趋势(图3)。最大容重值与峰值容重值均方误差MSE=0.0055,偏差率基本小于10%,占总样本的97.3%,且90%以上样本点的偏差率小于等于5%。平均容重与最大容重值的均方误差MSE=0.0285,偏差率10%以上的样本占16.52%,偏差率5%~10%的样本占49.19%,偏差率小于5%的样本占34.29%。
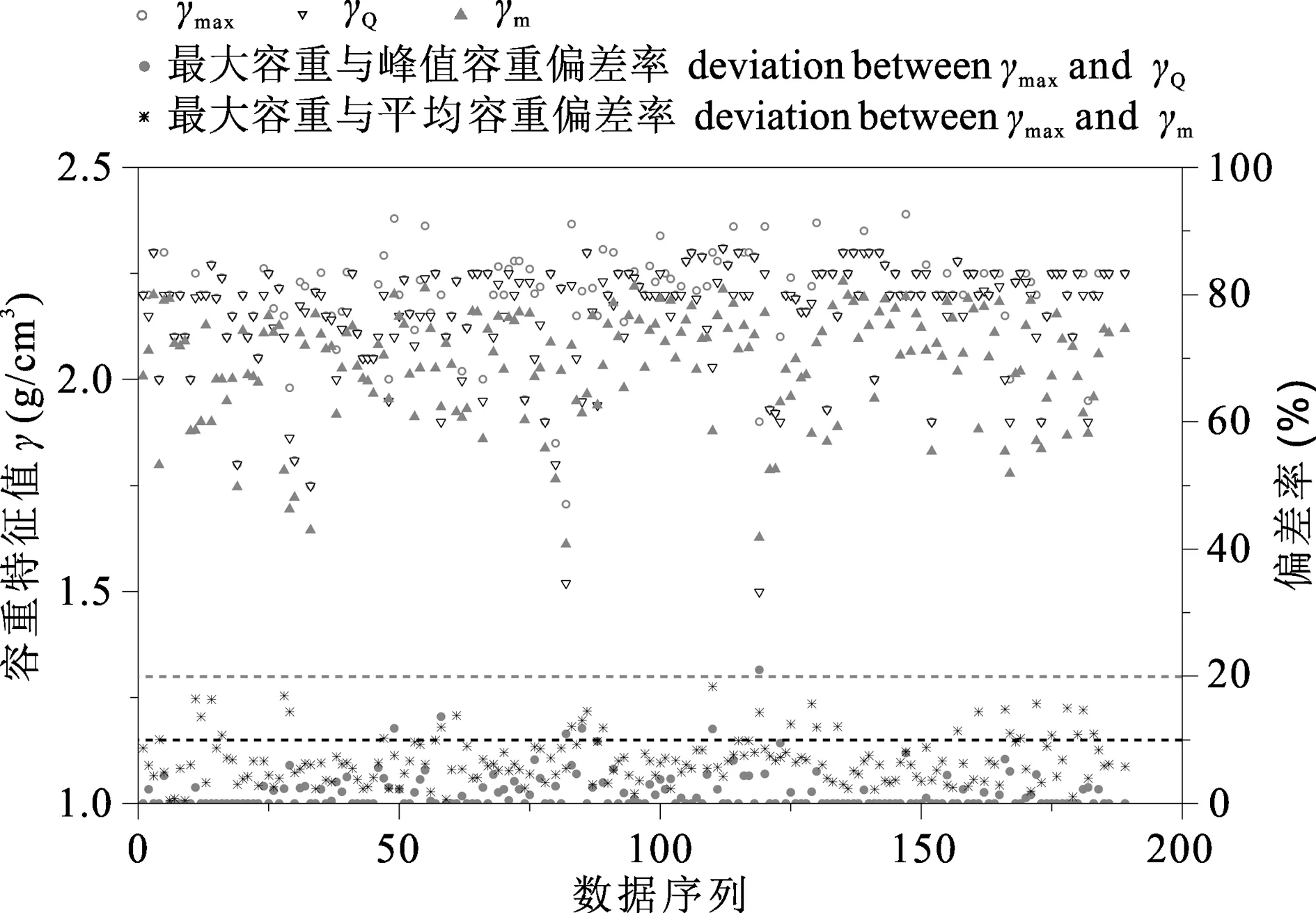
图3 容重特征值的数值分布及变化趋势Fig. 3 The distribution and changing trend of characteristic values of density
图3揭示了3个容重特征值之间的关联变化趋势,基于统计建立3个特征值之间的数量关系。结果显示,最大容重与峰值容重具有较好的线性关系,且可以通过式(5)进行转化计算,而平均容重与最大容重与峰值容重之间的关系可分别用式(6)和式(7)转化计算。
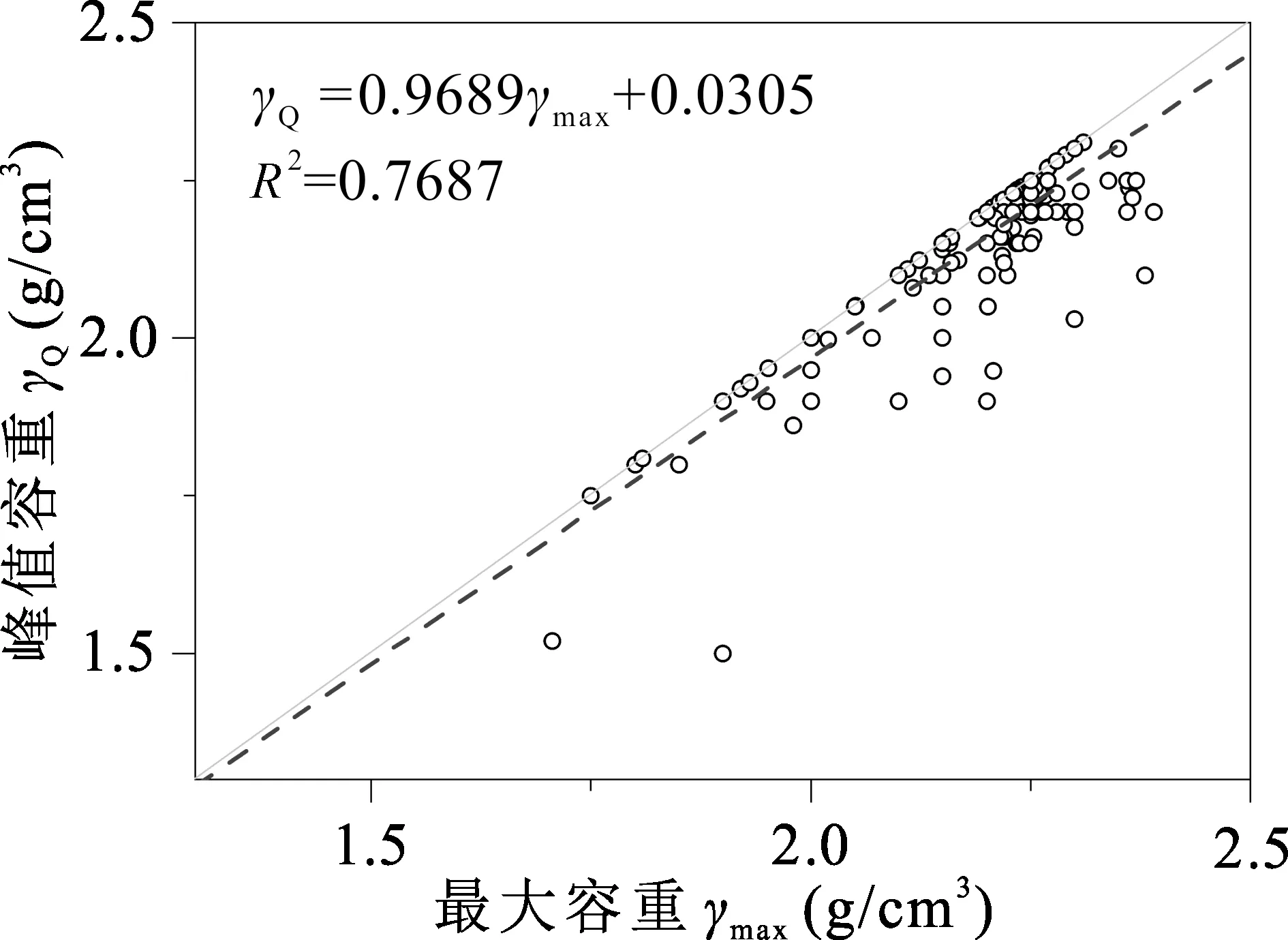
图4 最大容重与峰值容重的统计关系Fig. 4 The statistical relationship between max-density and peak-density
γQ=0.9689×γmax+0.0305
(5)
γm=0.8273×γmax+0.2292
(6)
γm=0.7580×γQ+0.4093
(7)
式中:γQ为泥石流峰值容重,g/cm3;γmax为最大容重,g/cm3;γm为平均容重,g/cm3。
从拟合曲线的趋势判断,平均容重分别与最大容重和峰值容重的拟合度基本接近,但根据泥石流的容重γ≥1.3 g/cm3的定义,从数值分布上看,最大容重与平均容重所得相关曲线可能更具有计算的适宜性。

图5 平均容重与最大容重的统计关系Fig. 5 The statistical relationship between max-density and mean-density

图6 平均容重与峰值容重的统计关系Fig. 6 The statistical relationship between mean-density and peak-density
3.3 运动特征对容重的影响
峰值容重与最大容重数值接近,前人已经建立了峰值流量与峰值容重之间的幂函数关系(Huang Hai et al., 2020),本文重点分析最大容重和平均容重两个容重特征值与灾害规模参数之间的相关性。图7和图8显示了流量特征分别与大容重和平均容重之间的相关性。为了描述流量特征,引入最大容重过流时的最大流量,分析结果表明最大容重值与最大容重时对应的流量极值具有较强的正相关,相关关系如式(8);而平均流量与平均容重之间相关性很弱,这与平均容重和平均流量的物理定义与计算方法不属于同一个框架导致的。
γmax=0.069ln(Qγ+5.873)+1.780
(8)
式中:Qγ为最大容重时对应的流量极值,单位m3/s;其他参数同前。

图7 最大容重与流量的相关关系Fig. 7 The relationship between max-density and discharge
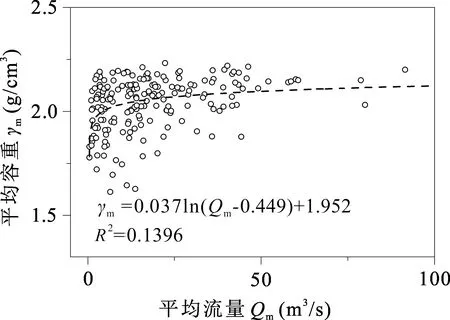
图8 平均容重与平均流量的相关关系Fig. 8 The relationship between mean-density and mean-discharge
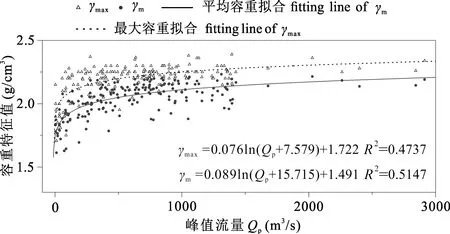
图9 容重特征值与峰值流量相关性Fig. 9 The relationship between the peak discharge and the characteristic values of density
峰值流量与最大容重和平均容重都有较好的相关性(图9),根据拟合关系分别建立最大容重与峰值流量、平均容重与峰值流量之间的关系式,如公式(9)和(10)。容重值与泥石流冲出总量之间没有明确的相关关系(拟合相关性系数R2<0.2),仅有总体上呈正比的趋势(图10)。
γmax=0.076ln(Qp+7.579)+1.722
(9)
γm=0.089ln(Qp+15.715)+1.491
(10)
式(9)和式(10)中各参数意义同前。

图10 容重特征值与冲出规模的相关性Fig. 10 The relationship between the hazards scale and the characteristic values of density
公式(9)和公式(10)所拟合的计算公式仅仅代表容重特征值与流量特征值之间的相关性,虽然物理意义和计算意义上似乎关联性弱,但从统计意义上看可以作为两者之间的一种校验关系进行应用。在操作层面上,最大容重和峰值流量都是泥石流灾害野外调查中较容易获得的参数,具有较强的实际应用价值。
4 泥石流容重取值方法优化
4.1 现有泥石流容重计算方法的评述
现有的泥石流容重计算方法对我们认识灾害特征、评价灾害风险、防灾减灾工程等提供了重要的依据。但从观测资料可知,一次泥石流事件的容重跨度很大,可从含沙水流—稀性泥石流—过渡性泥石流—粘性泥石流。在描述泥石流性质的时候,容重表达的是平均容重值,在计算泥石流峰值流量时,容重表达是峰值容重值,在计算冲压力的时候,容重表达的是最大容重值。这就导致计算所得的容重在工程设计计算中存在指向性的时空错位,且无法约束在现场采样等测试手段。基于以上的模糊概念,国内外建立了十余种容重计算方法,我们将具有典型代表性和广泛应用的12种进行对比分析,查明不同方法的建模依据、物理意义及计算误差来源(表2)。
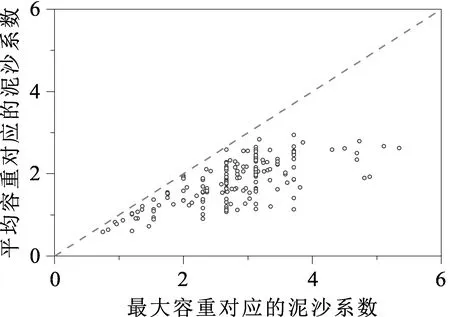
图11 不同容重值计算的泥沙系数差异Fig. 11 Difference of sediment coefficient calculated by different density value
4.2 容重特征值选取方法

图12 泥沙系数计算结果偏差率分布规律Fig. 12 Distribution of deviation rate of sediment coefficient calculation
在泥石流灾害治理与评价工作中,涉及到以容重为基础参数进行计算的灾害特征值主要有规模参数、动力参数、危险分析及工程结构参数4种类型,共7个特征值(表3)。在这些特征值中,最重要最直接的影响主要为峰值流量、流速、一次冲出固体物质量。我们从全流域空间尺度和全过程时间尺度来分析某一场泥石流灾害,可以发现泥石流的运动过程与容重的变化是具有密切关联的(王洋等,2017),在计算过程中容重通过一些耦合因子与运动特征之间建立起联系。因此基于该耦合关系可建立特征值计算时的容重选用原则,如表3。具体而言,峰值流量、流速、流体冲压力均应采取峰值容重,而排导槽纵比降设计则应采取最大容重,最大淤积范围、堵河分析和一次冲出固体物质量则应采取平均容重。但考虑实际情况中峰值容重的难获取和安全储备,在定量描述某次特定泥石流灾害时,建议选取最大容重和平均容重进行参数计算容重选取方法中主要涉及的参数更换的有峰值流量、流速和冲压力计算,结合前述最大容重与峰值容重的数值接近的统计规律(MSE=0.0055),将峰值容重更换为最大容重产生的误差将较小,且更有利于工程设计的可靠性。为了进一步说明新建的容重特征值选取方法的合理性和优越性,我们选择具有广泛应用和公认的较完善的泥沙修正系数和一次冲出固体物质量进行分析,结果如图11、图12和图13。
图11和图12揭示了平均容重和最大容重计算所得泥沙系数的差异,两者的偏差率具有明显的分区规律。具体为:① 当最大容重在2.32 g/cm3以上时,偏差率在40%以上;②当容重小于2.1 g/cm3时,偏差率一般小于30%,两者的计算具有一定的趋同性;③当容重为2.1~2.32 g/cm3时,偏差率10%~70%,这就使得我们无法确定计算结果的真实性。这种分区规律说明现有的计算方法在容重较小时,具有较好的吻合性,而当容重增大到2.0 g/cm3以上时,其不确定性显著增加。因此,从物理意义匹配上来说,峰值流量应采取峰值容重计算,采取平均容重计算将导致较大的偏差率,计算结果偏小,采取最大容重计算则有更大的安全储备,可能为解决当前拦挡工程溢流结构破坏难题提供新的途径(黄海等, 2020b)。

表2 国内常用的泥石流容重计算方法的物理意义及误差分析Table 2 The physical significance and error analysis of general formula of debris flow density in China

表3 泥石流特征值计算时的容重选取方法Table 3 Method of selecting density values for the calculation of characteristic values in hazards mitigation

图13 一次固体物质冲出总量计算的误差分析Fig. 13 Error analysis of the calculation of the solid materials in debris flow
图13展示了用最大容重计算所得一次冲出固体物质总量与实测值的对比,可明显看出最大容重值的偏差率分布,总体上泥石流灾害规模越大,最大容重计算所得的固体物质冲出量与实测的差异绝对值越大,但反而偏差率小;但同时灾害规模越小则差异绝对值虽然越小,但其计算偏差率反而越大,最大可达60%。进一步说明了对泥石流不同参数计算选取不同容重特征值的合理性和必要性。
4.3 容重值的获取与结果校验
从理论分析可以看出,容重独立取值计算较笼统取值计算具有明显的优越性。基于表2中建立的容重取值计算方法,针对关键参数最大容重值,我们可以进一步优化其野外获取方法。对于分析已发生的泥石流灾害事件来说,颗粒分析法是最具有实物依据的一种确定方法。基于颗粒分析法,从统计角度出发,我们建立一种针对泥石流历史事件的最大容重值取样分析方法(图14)。
新的方法共包括7个步骤:选取取样区—取样并测试土样粒径—计算每个土样对应的容重值—计算每个取样区容重值—确定该次泥石流最大容重值—计算平均容重值—校验计算结果。取样方法在原有的颗粒分析方法中对于样品采集无明确界定的情况下,多数实操过程往往采取一个样品代表一次泥石流事件(Ge Yonggang et al., 2013, 2014),为了进一步减小误差并规范化操作流程,将取样方法优化为以下步骤:① 选择沟道弯道凹岸侧为取样区;② 取样范围从沟口一直往上游延伸至流通区起点;③ 每个取样区至少采取3个土样。计算结果的检验主要通过分析容重值与现场调查所得的峰值流量之间的关系,并按照公式(9)和(10)进行校验计算,偏差率不超过15%则认为其结果为有效。
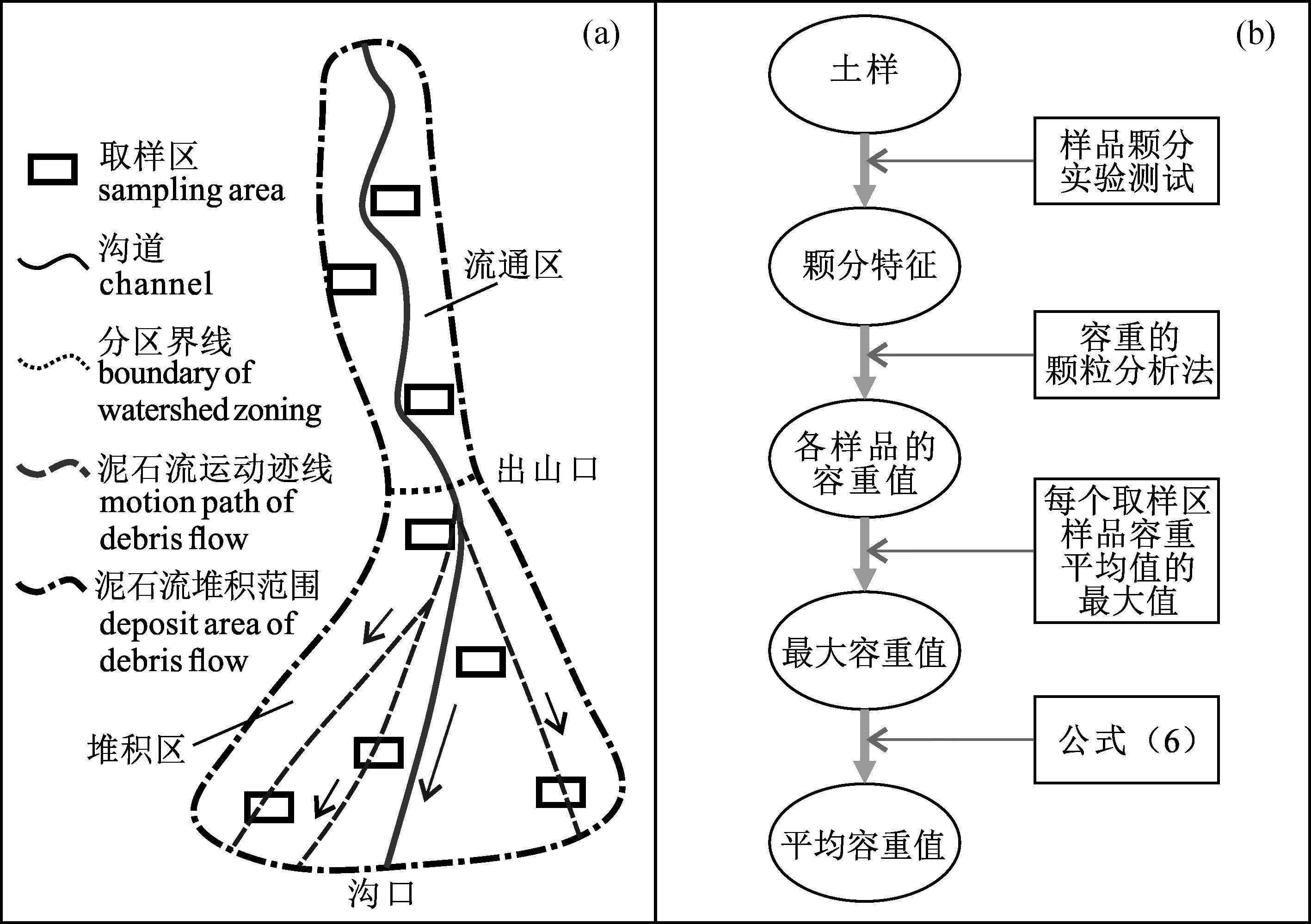
图14 泥石流容重取样分析方法流程图:(a) 容重取样方法; (b) 容重计算方法Fig.14 Sampling and analysis method for calculation of debris flow density:(a) the method of sampling; (b) the method of calculation)
5 讨论
(1)泥石流堆积物颗粒分析方法被诸多学者证明了其有效性和区域适宜性(蒋树和文宝萍,2012),但是这些方法都未明确界定计算所得的容重的物理意义,也没有确定该数值对泥石流过程的时空定位。甚至用于模型建立的武都等地的泥石流观测资料中针对一场泥石流也只有一个容重值,这与实际泥石流过程中容重的动态变化是不符合的。因此当我们将泥石流过程分解开来进行计算时,这个笼统的容重值就存在较大不足。泥石流特征值中的峰值流量、流速等是描述某一时刻的泥石流状态,物质输移总量则是描述泥石流全过程,用同一个概念下的容重值进行不同时空尺度上的非恒定流计算,是不匹配的。本文通过分析蒋家沟的观测资料,揭示不同尺度下的容重特征值的统计学规律,证明了将泥石流不同特征值计算分割开来的可行性。
(2)当前泥石流灾害特征值的确定存在最大的问题是对计算结果没有有效的检验方法,在工程实践中多数是靠工程师们的经验进行判断,甚至很多参数我们无法判断其结果与实际相比是偏大还是偏小。在泥石流灾害评价、治理中,学者们都有意无意的回避这个问题,尤其是开展泥石流全过程数值模拟的研究中,总是试图通过各种复杂的运动学、物理学函数进行计算,但在基础参数的变化中却缺少相应的描述(Ouyang Chaojun et al., 2019),这也导致我们对灾害过程模拟的结果总是会有疑虑,从而无法在工程实践中应用相关成果。在泥石流灾害治理中,尽管一般工程设计采取的是极端工况进行可靠度设计,但工程在抵御泥石流灾害后大部分都会出现损毁情况,如汶川震区、九寨沟景区等工程运行情况已经有证据证明了泥石流设计参数与实际运行的差异导致工程损毁(Liu Fangzhou et al., 2017;黄海等,2020b)。以上所述现阶段的防灾减灾实践更进一步说明了当前泥石流灾害基础物理参数上的不足已经成为制约防灾理论和技术的卡脖子问题,因此梳理这些参数,试图更加精细的描述泥石流流体特征将极大提升应用层面上的高度。
(3)泥石流灾害治理工程设计中的动力参数计算,如流速、峰值流量、冲压力、冲出总量等,均是有着明确的物理意义和时空定位。利用本文建立的新的模型来确定容重参数作为灾害动力参数计算的基础参数,原理清晰,物理过程明确,且具有一致性的时空定位,将大大提高计算的准确度和可校验性,是泥石流灾害治理工程实践的重要进步。同时,在灾害全过程模拟时,将容重进一步刻画,大大提高了泥石流运动过程和物质交换的连续性。
(4)基于容重特征值的统计学关系建立的取值方法和检验方法是基于蒋家沟的完整观测数据,可能在区域适宜性上还存在不确定性。但受限于我国目前泥石流的观测资料缺失,除了蒋家沟之外,还未有泥石流灾害全过程监测数据,同时室内试验由于规模尺度效应,流体时空差异性和取样难题都制约了理论模型的完善,因此还需要通过不同区域的观测数据和更大尺度的室内外实验进行模型修正。
6 结论
(1)为了能在工程设计中精确化分析容重参数,根据容重的物理意义和时空变化规律,本文引入最大容重、峰值容重和平均容重来刻画一次泥石流事件的容重特征。利用蒋家沟1987年以来的观测数据,统计分析了3个特征值的相关性并建立了相互转换计算公式。
(2)最大容重与峰值容重的时序关系与泥石流灾害物质输移集中度密切相关,时序特征值越小,泥沙输移越集中,流量过程线尖峰状越明显,则将最大容重和峰值容重统一取值可信度越高。平均容重和最大容重均与泥石流峰值流量呈现对数函数关系,而与泥石流冲出规模总量无关,基于此建立了流量参数与容重特征值的统计关系式,其可用于容重取值结果的校验。
(3)防灾减灾工作中,建议采取最大容重来计算泥石流的峰值流量、流速、排导槽纵比降确定以及流体冲压力,采用平均容重计算泥石流的一次固体物质总量、堵河可能性以及危险范围。
(4)基于颗粒分析法,进一步优化了现场样品采集方法,规范了取值过程中选取取样区—取样并测试土样粒径—计算每个土样容重值—计算每个取样区容重值—确定该次泥石流最大容重值—计算平均容重值—校验计算结果的七个操作步骤。优化计算方法可有效减少取样误差,并解决了目前泥石流容重确定的概念模糊和校验缺失问题。研究结果对泥石流灾害防治具有重要支撑作用

