属性和亲密度关系兼顾的影响力研究
胡健宇,章 静,许 力,林力伟
1(福建工程学院 计算机科学与数学学院,福州 350118) 2(福建工程学院 福建省大数据挖掘和应用技术重点实验室,福州 350118) 3(福建师范大学 福建省网络安全与密码技术重点实验室,福州 350007)
1 引 言
社交网络是用来描述群组中个体之间的关系和交互的工具[1],是人们进行发布和传播信息、交流互动和工作学习的平台.其中,影响力是社交网络分析的重要工具,是研究网络信息传播机制、社会舆情分析的理论依据.在网络中,用户节点依据自身的影响力传播信息,影响力表示网络中节点能承受的最大信息量[2].社交网络影响力广泛应用于舆论传播、群体行为的形成和发展等重要领域[3],同时,随着网络容量和规模的逐渐扩大,网络的安全隐患逐渐增多,对用户的攻击也会影响网络中信息的传播.因此,深入探索网络中的信息传播机制,可以有效地防止网络攻击对信息传播的不利影响.例如,在微博平台上,社会信息主要通过一些影响力较大的用户通过网络中的社交关系传播出去,影响着人们的生活,而虚假的社会信息经过这些用户,将会引起社会的骚乱,更有甚者会损害部分用户的名誉,危害个人财产.信息的传输时刻改变着人们的生活方式,并且影响力越大的人传播信息能力越强,因此,挖掘影响力较大的用户至关重要.生活中,网络红人利用自身影响力吸纳粉丝以赚取流量;资本家以此来推销商品;政治家依靠影响力来笼络人心[4],等等.同时,当部分用户受攻击时,受攻击用户的朋友可能无法及时得到消息,对人们的生活造成不利影响.
所谓影响力最大化问题,也就是从已知的社交网络中,挖掘出k个影响力最大点的集合,使得这些节点通过一定的传播模型进行信息扩散,观察信息传播的最大范围.常用的影响力最大化度量方法是从社交网络中的内部结构出发,研究各节点之间的参数,例如各节点的最短路径、度数、介数等等,来衡量节点的影响力,例如,贪心算法[5],每次选择的节点集合都可以达到当前最大的传播效果以度量各节点社交影响力;度中心性算法[6],选择网络中度数最大的节点集合.这些算法通过社交网络结构挖掘传播特性最大的节点集合,然而,它们缺少对社交网络内部信息的深入挖掘,例如,网络中邻居节点间的亲密度[7],即两个互为邻居节点之间的亲密程度,邻居节点之间的亲密度越高,反映朋友之间的关系越亲密,忽略潜在的信息的度量算法无法准确反映社交网络之间的人际关系,从而限制了网络中各节点在各传播模型下的传播扩散能力.同时,随着互联网技术逐渐发展,社交网络的结构越来越复杂,网络的安全性也难以保证.
本文基于现有影响力算法的不足,深入挖掘用户属性和亲密度之间的潜在关系,提出一种属性和亲密度兼顾的影响力算法,有效提高了网络传播能力和网络传播的抗攻击性.其主要贡献如下:
1)定义了一种基于属性的朋友亲密度度量关系,用于测量社交网络中各用户之间的亲密度,量化朋友之间的亲密关系,构建社交网络亲密度矩阵.
2)在属性测量得到亲密度矩阵的基础上,根据概率模型,提出一种基于属性与亲密度关系的游走算法(Social Influence Measurement Algorithm based on intimacy Random Walk,SIMARW),选择出具有高影响力及抗攻击性的种子节点,提高网络传播及抗攻击能力.
3)在真实网络中,对该算法的影响力传播效果进行实验评估,分析得出 SIMARW算法在传播效果上和抗攻击能力上的有效性.
2 相关工作
目前,贪心算法[5]、影响力启发式算法[6-8]、基于随机游走的影响力度量算法[9]是3种不同的影响力度量算法,它们的相似处在于:3种方法都是依据社交网络的结构来获取影响力最大的节点集合.然而,这些研究方法仅仅是依据网络中的点边分布关系,忽略了各用户的社会属性,对网络中潜在信息的挖掘不够.社交网络中隐藏的潜在信息,例如,朋友之间的属性关系,互动频率等等,这些信息会在一定程度上反映网络中用户的社交能力和社交影响力.传统的度量算法忽略了这些隐藏信息,没有准确地反映节点在网络中的传播能力.同时,过于依赖网络结构信息传播的算法在信息高风险下的社交网络中安全性很低,一旦网络遭到攻击,网络结构被破坏,会极大地影响节点的传播能力.因此,挖掘社交网络中的潜在信息对研究网络的扩散机制和保护网络的传播机制有着重要意义.因此在影响力传播范围存在一定的问题,同时,依据社交网络结构的算法在个人隐私高风险状态下的抗攻击性存在缺陷.
因为贪心算法存在效率低下的问题,一些学者提出了一些启发式算法,例如文献[6]提出了基于度的启发式算法,也称为”Digree Discount”;文献[8]提出一种基于k-核的影响力启发式算法.这些算法耗时较短,效率高,但它们在不同的社交网络和不同的传播模型下传播范围不稳定.同时,为了可以准确测量各节点的影响力,一些学者提出了基于随机游走的衡量算法,例如PageRank算法[9],最初是由Google公司提出,以衡量各网页的影响力,而后被运用于节点影响力测量上,该算法可以测量各节点的影响力,但该算法对影响力的衡量上也仅仅取决于各节点之间的关系,对用户之间的潜在信息挖掘太少,在影响力测量的准确度方面还不够.
近年来,很多学者试图通过挖掘多种潜在信息进行社会影响力研究.例如,文献[13]中将情感因素作为潜在信息进行社会影响力算法研究;文献[14]中将社会中竞争信息纳入影响力最大化问题中,设计了一种基于主题模型的节点之间影响概率计算方法;文献[15]中通过挖掘网络中用户间的互动与影响力之间的关系进行影响力度量.但同时,这些对潜在信息挖掘算法忽略了节点属性的影响,节点的情感极性、竞争传播以及交互行为等研究都不离开对节点属性的研究,因此在潜在信息的挖掘上存在缺陷,本文的设计能有效地缓解此类问题.
3 模型构建和相关定义
为深入探索社交网络及网络中的潜在信息,本节给出社交网络的模型构建和相关定义.
3.1 社交网络模型
定义1.(社交网络)[16]给定网络G(U,E,χ),其中,U表示在网络G中的用户集合,E表示在网络G中的社会关系集合,χ表示在社交网络G中的用户属性集合.其中,ui,uj∈U表示网络中的两名用户,ei,j表示用户ui和uj之间的朋友关系(其中ei,j∈E,同时,ej,i∈E),|U|和|E|分别表示在网络中节点和边的总数.
其中对于网络中任一用户ui(其中ui∈V),其属性集设定为χi∈χ(1≤i≤|V|),其中|χi|表示用户属性的总数,其中,属性xj∈χi(1≤j≤|χi|)是针对其对应的属性类别Aj∈A(1≤j≤|A|),其中,|A|表示在社交网络G中的所有类别集合的总数,举例如下.:
A={(A1=最喜欢的书籍),(A2=最喜欢的运动),(A3=最喜欢的电影)}
U={(u1=张三),(u2=李四)}
χ1={(A1:《傲慢与偏见》),(A2:跑步),(A3:速度与激情)}
χ2={(A1:《简爱》),(A2:篮球),(A3:冰雪奇缘)}
其中,用户u1和u2具有朋友关系,e1,2∈E,e2,1∈E.
3.2 传播模型
定义2.(独立级联模型(Independent Cascade Model,ICM))[17]在该模型中,将网络中的节点分为活跃节点和不活跃节点两种状态节点.其中,活跃节点会尝试激活不活节点,不活跃节点被激活后成为活跃节点,便可以尝试去影响其他邻居节点.假设存在节点i在t时刻被激活为活跃节点,而对于i的邻居j是不活跃节点,pi,j为i激活j的概率.当节点j被激活,则在(t+1)时刻进入活跃状态;反之,j仍处于不活跃状态.
定义3.(线性阈值模型(Linear Threshold Model,LTM))[17]在该模型中,一个节点的传播状态是否会受到影响取决于该节点与邻居节点之间的共同影响力.对于一个不活跃节点w的邻居节点v,bv→w表示节点v对节点w的影响力,则有∑vbv→w≤1.在该模型中,当它们之间的共同影响力总和超过设定阈值θw时,则节点w被激活.即满足式(1):
∑vbv→w≥θw
(1)
时,节点w被激活,转变为活跃状态.θw反映了节点在模型中被激活的倾向性,θw越大,节点w就越难被激活.
4 基于亲密度随机游走的社交影响力度量算法
社交网络中节点间的属性关系会影响节点之间的亲密关系.本节将介绍如何通过已知的属性计算朋友之间的亲密关系影响,计算朋友的亲密度大小,而后根据随机游走的基本思想,测量社交网络中各节点的社交影响力.
4.1 基于属性和亲密度关系的亲密度度量算法
在社交网络中,朋友之间的属性关系会极大地影响双方的亲密关系.其相关原理如下:
1)在单个用户中,将该用户的相同爱好属性的朋友和不同爱好属性朋友分为两个集合,而后,依据加权级联模型[17]对朋友关系的反映原理,计算其概率影响.所谓加权级联模型,是独立级联的一种特殊传播模型,其节点激活表达式如式(2)所示:
pv,w=1/d(w)
(2)
其中,v,w为两个节点,d(w)表示节点w的度数,pv,w表示处于活跃状态的节点v激活其不活跃邻居节点w的激活概率.式(2)表示在网络中,朋友数量越多的用户节点被单个朋友影响的概率越小,在单个属性下,根据用户是否拥有该属性,将用户分为属性相同集合和属性不同集合,并据此进行亲密度概率计算;
2)节点的多个属性相互独立.
依据以上的原理,计算节点之间属性亲密关系如下:
(3)
P(i→j)=P(i→j)A1·P(i→j)A2·…·P(i→j)An
(4)
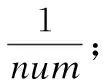
在式(3)和(4)中,A1,A2,…,An表示n个相互独立的不同属性,依据式的计算方法可以求出节点i对节点j的属性亲密关系影响.
该属性亲密计算步骤如下:
算法1.基于属性和亲密度关系的亲密度度量算法(Intimacy Measurement Algorithm based on attribute and Intimacy Relationship,IMAAIR)
输入:用户集合V,社会关系集合E,属性集合矩阵Attribure[N][M](N表示节点用户数量,M表示属性数量)
//当Attribure[i][j]=1时,用户的配置文件中有此属性,反之为Attribure[i][j]=0.
输出:属性亲密关系矩阵PAttribure[N][N]
1.IntializePAttribure[i][j]=1(i∈[0,N),j∈[0,N))
//属性亲密关系矩阵PAttribute初始化
2.Calculatedegree[i] (i∈[0,N))
//根据社交网络结构,计算节点用户i的度数degree[i]
3.Calculatenum[i][s](i∈[0,N)j∈[0,M))
//计算每位用户在各个属性下相同人数
Intializenum[i][s]←0 //初始化
ifAttribute[i][s]==Attribute[j][s](i≠j) do
num[i][s]++
4.fors=0toMdo
ifAttribute[i][s]==Attribute[j][s](i,j∈[0,N)andi≠j)
else do
end for
//计算属性亲密度矩阵
5.return PAttribute
//返回属性亲密度矩阵
4.2 基于亲密度随机游走的社交影响力度量算法
基于游走的度量算法作为社交网络影响力度量算法之一,这些算法依据节点的数量和质量进行均匀概率游走,计算出各节点的影响力大小[18].
本文以矩阵形式表示社交网络中的用户关系,对基于随机游走的社交影响力度量算法原理进行介绍:在初始状态时,对社交网络中每一个节点都赋予1个PR值,用矩阵的形式表示社交网络中的初始状态(0状态)为:

(5)
(6)
(7)
其中degreej指节点j的度数,edgeij指节点i和j之间的社会关系,当edgeij=1,则表示节点i和j存在朋友关系;反之,则两节点用户之间无朋友关系.
基于随机游走的影响力算法,可以量化各节点的影响力,但同时,该算法仅仅依据网络中每个节点用户的朋友个数进行随机游走.然而,在现实社会中,朋友之间的亲密关系不同,基于朋友个数的均匀概率游走算法无法表现不同朋友的亲密关系,对社交网络中的挖掘的信息有限,所获得的影响力传播效果有限,同时随机游走算法过于依赖社交网络的结构,一旦网络结构遭到攻击,传播能力将会受到不利影响.因此,本文在研究属性和亲密关系的基础上,对原有的随机游走类算法进行改进,得出了基于亲密关系的社会关系矩阵,并据此计算各边的游走概率,度量各用户的社交影响力,寻找影响力较大的节点集合.

算法2.基于亲密度随机游走的社交影响力度量算法(Social Influence Measurement Algorithm based on intimacy Random Walk,SIMARW)

输出:被选择出的种子节点集合seed_nodes
1)PR[i]=1(i∈[0,N))
//PR初始化,初始设定为1,其中N为节点个数
2)sum[i]←PAttribute[j][i](i∈[0,N),j∈[0,N))
//计算游走概率矩阵
3)fori=0 toTdo
end for
//通过SIMARW算法,计算出各节点的PR值(即影响力)
4)Intializeseed_nodes≠Ø//seed_nodes种子节点初始化
fori=1 tokdo
u←argmax(PR)
seed_nodes.apend(u)
end for
//选出社交网络影响力排名前k个节点所组成的集合
5)returnseed_nodes//返回种子节点集合
算法复杂度分析:SIMARW算法是基于属性和社会关系进行迭代随机游走的算法,通过属性计算属性亲密关系的复杂度为O(s*(m+n)),计算各边之间的亲密关系概率(也就是权值)的复杂度为O(n*m),在亲密概率基础上随机游走,通过遍历节点的度来计算分配的节点的影响力的复杂度为O(t*(n+m)),其中s为属性数,t为迭代次数,n为网络中的节点数,m为网络中的边数,k为选取的初始节点数,因此SIMARW算法的时间复杂度为O((s+t)*(m+n)+n*m).本文使用邻接表来存储数据网络,SIMARW算法的空间复杂度为O(m+n+s*n).
5 实 验
5.1 实验环境
本文的算法采用python来实现的,实验平台是python的开发工具:pycharm,所有的实验都是在一台 PC 机上运行的,PC机的配置如下:Intel(R)Core(TM),2.50GHz,内存8.00GB,Windows7操作系统.
5.2 实验数据
本文采用SNAP Facebook数据集(1)http://snap.stanford.edu/data/ego-Facebook.html进行实验,该数据集包含了用户之间的人际关系,以及各用户的多个属性,被多次应用于影响力分析,隐私保护以及用户行为预测等多个领域,文献[20]中使用该数据集进行社交关系和隐私保护实验研究.该数据集包含10个匿名网络,本文选取其中的5个网络,并从每个数据网络随机抽取50个属性进行实验.本文分别使用线性阈值模型和独立级联模型进行实验.实验数据如表1所示.

表1 数据集列表Table 1 Dataset list
该社交网络数据集包括社交关系数据集.edges和节点属性数据集.feat,其中属性数据集中包含有大量的属性维度,在数据集中,如果用户的数据配置中有某一属性,则该用户在该属性上为1,否则为0.为了防止属性的名字暴露个人信息,这些属性都被匿名化了.
5.3 实验及结果分析
为了检测该算法的实验效果,验证挖掘网络中的潜在信息对网络传播效果的影响,本文使用基于网络结构而未挖掘潜在信息进行影响力度量的随机算法(Random)、贪心算法(Greedy)、度中心性启发式算法(Degree Discount)和基于反向PageRank的影响力最大化算法(MPRD)[21]进行对比.
随机算法(Random):从网络中随机选择出k个节点作为初始活跃节点集合
贪心算法(Greedy):贪心算法能够保证,每次选择的节点集合都可以达到当前最大的传播效果[22],进行10000 次模拟,即R=10000,R为实验次数.
度中心性算法(Degree Discount):从网络中选择出k个度最大的节点集合作为初始活跃节点集合.
基于反向PageRank的影响力最大化算法(MPRD):一种混合反向 PageRank 和度中心性的启发式算法,基于该算法,从网络中选择出k个影响力值最大的节点作为初始活跃节点集合,根据文献[21]中结论,s取0.2.
基于亲密度随机游走的社交影响力度量算法(SIMARW):从网络中选择k个基于游走概率最大的节点集合作为初始活跃节点集合.
将上述3种算法选出的节点作为种子节点集,分别在线性阈值模型和独立级联模型两种传播模型下进行实验,同时,本文采用传播效果和抗攻击性两个指标进行衡量(见表2).5.3.1 传播特性对比

表2 算法复杂度对比Table 2 Comparison of algorithm complexity
本节通过实验比较SIMARW算法和影响力节点集合算法进行比较,将最终的传播范围作为评价指标.在线性阈值模型实验中,在缺少阈值信息的情况下,为了提高实验效率,网络中节点的阈值设置为相同值0.5,并且认为网络中每个节点中的各邻居对其影响是相同的[12].同样,在独立级联模型(ICM)实验中,为提高实验效率,将节点之间的激活概率均设为相同值0.01[12].为了保证实验准确性和客观性,最终结果取100次实验的平均值.
各网络分别在线性阈值模型和独立级联模型下的影响力传播效果对比图如图1和图2所示,其中,横坐标为种子节点个数,纵坐标为激活节点数.

图1 线性阈值模型下各网络影响力传播效果图Fig.1 Diagram of the effect of the network influence under LTM
图1(a)、(b)、(c)、(d)和(e)为该5个网络分别在线性阈值模型下的传播效果图,从5个网络图的传播效果可以发现,Random算法的传播效果最差,这是因为Random算法通过在网络中随机选取节点,未对网络进行深入的挖掘.从(a)图中可以发现,当种子节点较少的时候,SIMARW算法的传播效果低于其他两种算法,在种子节点数量达到110后,相比于贪心算法和度中心性算法,SIMARW算法具有更好的传播效果.同时,在该数据集中的3个算法下会出现传播范围跃升后保持相对稳定的情况,Greedy算法下的种子节点数为20时传播范围从51跃升至186后并保持稳定;Degree算法下的种子节点数为19时传播范围从44跃升至173后保持相对稳定;同时SIMARW算法在种子节点数量较低时虽然传播效果不如其他两种算法,但一直保持稳定增长的态势,并在种子节点数达到130时传播范围跃升至306,而后传播范围保持稳定.这是因为在该线性阈值传播模型下,随着种子节点数量不断增多,其邻居节点中活跃节点的数量也越来越多,激活节点的数量也越来越多,这些激活节点从不活跃状态进入活跃状态,并开始去影响其他节点,这加速了信息传播扩散的速度,导致了图1(a)中传播效果的跃升,同时,信息传播突变以后,网络中的信息传播到达极限,扩散开始趋于平稳.
图1(b)、(c)、(d)和(e)分别为107号、348号、686和1912号网络在线性阈值模型下的传播效果图.从图1(b)中可以发现,当种子节点数较小时,贪心算法和度中心性启发式算法的传播效果略优于SIMARW算法,从种子节点数为36时起,SIMARW算法激活节点数为42,而贪心算法和度中心性算法为39,SIMARW算法相比其他算法,表现出更优的传播特性;图1(c)中,在种子节点数为12时,SIMARW算法的激活节点数为15,超过其他两种算法,并且随着种子节点数量增多而加速增长.图1(d)和图1(e)中种子节点数分别为52和40时,SIMARW算法的传播效果要优于其他算法.从图1中5个网络的传播效果图中可以发现,MPRD算法的传播效果在种子数目较大时要优于其他3种传统经典算法,这是因为MPRD算法对社交网络进行了更为深入的挖掘,将度中心性算法的挖掘思想引入了PageRank算法中,但该算法缺乏对潜在信息的挖掘,因此其传播效果不如SIMARW算法
从图1中3个网络的传播效果图可以发现,在线性阈值模型下,SIMARW算法在种子节点数目较大时有着更好的传播效果.
图2(a)、(b)、(c)、(d)和(e)表示在独立级联传播模型下各个算法在各网络图中的传播效果,图2(a)中,种子节点数较小时,贪心算法的传播范围要优于其他算法,SIMARW算法的激活节点数略高于Random算法,当种子节点数量达到72时,SIMARW算法下的激活节点数超过其他算法,MPRD算法优于其他传统算法,但略低于SIMARW算法;同样,图2(b)中,在种子节点数量达到28时,SIMARW算法的传播效果开始优于其他算法;图2(c)中SIMARW算法的优越性相对来说不明显,SIMARW算法在一开始节点增长速度平缓,当初始节点数为45时,SIMARW算法的激活节点数开始优于其他算法;图2(d)中SIMARW算法在初始节点数达到40时,传播效果优于其他算法;图2(e)中在种子节点数为74时,SIMARW算法优于其他算法.

图2 独立级联模型下各网络影响力传播效果图Fig.2 Diagram of the effect of the network influence under ICM
从图2中独立级联模型下的实验结果可以发现,种子节点数较小时,贪心算法的传播效果优于度中心性启发式算法和SIMARW算法,但是随着种子节点数目的增长,贪心算法和度中心性算法在传播效果上增长幅度逐渐平缓,而SIMARW算法显示出更好的传播效果.
从图2中可以得出以下结论:在独立级联模型(ICM)中,在种子节点数量较少时,Greedy算法和Degree算法的传播效果要优于SIMARW算法和MPRD算法,但随着节点数量增多,SIMARW算法在传播效果上显示出一定的优越性,MPRD算法效果略低于MPRD算法,而Random算法因为挖掘网络中各节点的相关关系,所以传播效果最差.
5.3.2 抗攻击性对比
所谓抗攻击性,指在部分节点受到攻击而失去传播能力的情况下,社交网络与未受到攻击情况下在传播效果上的下降程度.本文通过受攻击影响程度来衡量算法的抗攻击性,受攻击影响程度(s%)的定义如式(8)所示:
(8)
在式(8)中,N0表示未受到攻击状态下的社交网络中激活节点数,Nattack表示受到一定程度攻击状态下的社交网络中激活节点数.受攻击影响程度表示在个人隐私高风险状态下,一定程度节点被攻击对社交网络传播效果的不利影响.因此,受攻击影响程度越小,抗攻击性越大;反之,则抗攻击性越小.同时,当N0≤Nattack时,该算法在受到攻击下的传播效果没有受到影响.
网络0在10%至50%程度隐私攻击下Random、Greedy、Degree、MPRD和SIMARW算法在传播扩散上受攻击影响程度对比图如图3所示,从图3中个体受攻击影响程度比较发现,Random算法的受攻击影响程度最小,因为Random算法随机挖掘网络种子节点,受到攻击后影响程度小.除Random算法以外,SIMARW算法受攻击影响相对最小,抗攻击性相对最高,并且,从图(c)、(d)和(e)中发现SIMARW算法几乎没有受到攻击影响,产生这种现象的原因与算法的原理有关,Greedy算法和Degree算法都是基于社交网络结构进行测量,并且对网络图结构的挖掘程度有限,因此一旦网络节点遭到攻击,网络的传播能力就会受到影响,MPRD算法为反向PageRank算法,在PageRank算法中引入了度中心性算法,对原有的网络图进行了更深入的挖掘,因此受攻击影响程度相对于Random算法和Degree算法较低,但该算法并未深入挖掘网络中的潜在信息,相比之下,SIMARW算法通过属性和亲密度之间的潜在关系来度量网络的传播能力,因此破坏网络结构不会对其传播能力造成影响.
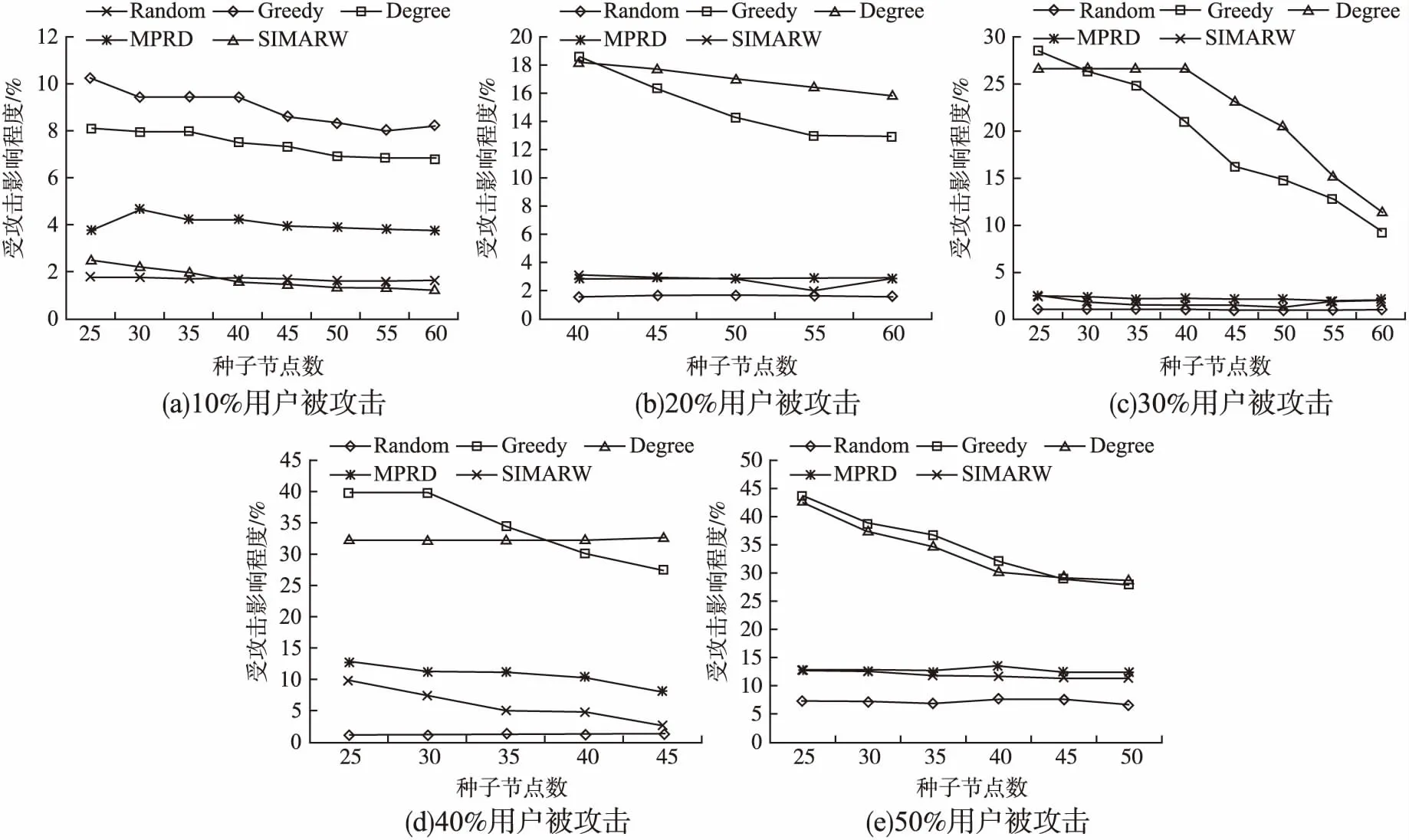
图3 在网络0中高度个人隐私风险模型下的抗攻击效果图Fig.3 Effect of influence propagation under the high individual risk attack model in Network 0
6 结 语
针对现有算法在选择网络传播种子节点上没有反映社交网络中的潜在信息,且未考虑社交网络结构遭到破坏,网络的传播能力将会受到影响这一问题,本文定义了一种基于属性的朋友亲密度度量关系,量化其对影响力的衡量,在此基础上提出了一种基于属性和亲密度关系的游走算法(SIMARW),该算法综合考虑了网络的结构、属性和亲密度三者之间的关系,选择出具有高影响力及抗攻击性的种子节点,提高网络传播能力及抗攻击能力.实验过程中使用SNAP数据集,采用传播效果和抗攻击性两个指标,将SIMARW算法与Random算法、Greedy算法、Degree算法和MPRD算法进行对比,通过实验证明了该算法在传播扩散上的有效性,以及在高隐私风险状态下的社交网络中SIMARW算法具有较好的抗攻击性.
本文的算法探索属性和亲密度之间的关系,仅仅用于分析社交网络中的用户评估,在后续的工作中,研究将思考将本文设计的算法应用于广大领域,如当下疫情传播模型分析,仿真出传播模型,寻找出传播影响力最大可能人员,对其进行尽快隔离和监控;商业传播,5G发展下越来越多用户通过视频推送获取商品信息,仿真出推广模型,寻找出影响力最大化节点,对商品的推广有着重大的意义等等.

