直流电机双闭环调速系统的动态仿真
查竞舟 王磊
1.南昌航空大学科技学院;2.湖南交通工程学院
针对转速单闭环直流调速系统起动过程中电流较大问题,提出一种基于PI控制的双闭环直流调速系统,按照先内环后外环的顺序对调节器进行分析和设计。在Matlab/Simulink中构建了其动态数学仿真模型,并按照工程设计中计算得到的PI参数进行仿真,模拟直流电动机起动过程。仿真结果表明,双闭环直流调速系统能够不仅实现时间最优起动过程,并且具有较好的动态跟随性能和抗扰性能,仿真结果符合工程设计要求,表明该仿真模型的设计是科学合理的。
文献[1]提出的仿真模型重点只关注了转速动态响应,但从电流响应曲线发现,最大电流接近16kA,这是没有意义且不符合控制系统的实际情况。转速、电流双闭环直流调速系统则可以解决这个问题,且能够保证在起动过程中,起动电流始终为电流允许最大值,使直流电机已最大加速度完成起动过程。当转速达到给定值以后,转速调节器ASR立即进行调节,保持稳定转速运行。起动结束后,电流迅速下降,经电流调节器ACR调节,最终电枢电流Id维持在负载电流IDL附近。因此,该系统能够实现时间最优起动过程。在需要频繁进行正反转切换的场合,尤其是精密机床、高精度机床等,这种时间最优起动非常重要,可大大提高加工速度[1]。
转速电流双闭环直流调速系统具有很好的稳、动态性能,结构简单,可靠性高,应用非常广泛。利用工程设计方法来确定其ASR和ACR参数,遵循先内环后外环的原则,在Matlab/Simulink中搭建基于动态数学模型的仿真模型,并对仿真结果进行分析[2]。
1 工程设计
一PWM变换器供电的双闭环直流调速系统,其开IN=52.2A,nN=2610r/min,Ce=0.1459V·min/r,λ=1.5,关周期Ts=0.000125s,直流动电机数据:UN=400V,R= 0 .3 68 Ω ,电磁时间常数Tl=0.0144s,机电时间常数Tm=0.18s,T0i=0.0006s,Ton=0.01s,Ks=107.6,=10V,Uim=8V,Ucm=5V。设计指标:要求转速稳定后静差率为0,电流超调量σi≤ 5 % 电动机不带任何负载起动到额定转速nN时的转速超调量为σn≤ 5 % 据此,经过具体计算可以得出电流反馈系数,转速反馈系数
1.1 ACR的设计
设计要求电流调节无静差,因此,电流调节器中必须包含积分环节,而电流环内被控对象中不含积分环节,故需要把整个电流环校正成典型I型系统即可,并且以跟随性能为主,超调小(σi≤ 5 % )。因此,电流调节器ACR可采用PI调节器,该环节特性为。电流环的开环传递函数为校正成I型系统时,可利用零极点对消原理,令,τi=Tl以使分子中τis+ 1环节和分母中的大大惯性环节抵消[3],这样可以提高系统的响应速度,故。但应该注意,当用实际的运算放大器实现系统时,由于参数可能会产生温度漂移或者其他干扰因素的存在,很有可能导致这种零极点对消不准确,这样可能会导致整个系统不能稳定工作的严重后果,此时必须考虑温度漂移等因素的影响并采取抑制温度漂移的措施[4]。另外,由设计要求可以看出电流只是略带超调,没有特殊要求,因此可选择阻尼比, 对应,即可确定,其中。最后,在把电流环校正成I型系统过程中,忽略了反电动势变化对电流环的影响和PWM变换器非线性因素的影响,且对电流环进行了小惯性环节处理,因此,必须分别对其进行近似校验,只有满足近似处理条件,上述分析才成立[5]。有关近似处理条件和具体计算,可查阅文献[5]。经计算,该设计均满足以上近似处理条件。
1.2 ASR的设计
有关参数的确定:2T∑i=2×0.000725=0.00145s, T∑n=2T∑i+Ton=0.01145s,ASR调节器传递函数在确定Kn、τn时,要同时考虑转速跟随性能和抗扰性能均较好的原则进行确定,为此,选择h=5,则计算得出Kn=99.593。在完成所有参数计算后,需要校验是否满足电流环传递函数简化条件以及转速环小时间常数近似处理条件,否则上述设计方法同样不成立。
1.3 ASR退饱和超调量的校验
由文献[5]可知,当h=5时,将转速环设计成典型II型系统,在阶跃输入作用下其跟随性能指标为37.6%,大于工程设计要求10%,似乎上述设计不合要求。实际上它是在ASR为线性环节下得出的,而在直流电动机启动过程中,ASR始终是饱和的,在饱和限幅的非线性作用下,转速超调量会大大降低,因此,显然是不合理的,实际的转速超调量应该在起动过程结束后,ASR退饱和后进行计算。
2 校验近似条件
2.1 电流环
(1)电流环截止频率
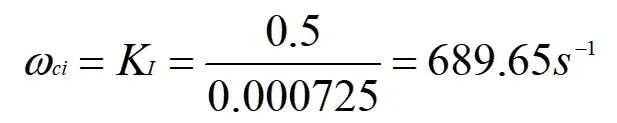
(2)晶闸管整流装置传递函数的近似条件
(3)忽略反电动势变化对电流环动态影响的条件
(4)电流环小时间常数近似处理条件
2.2 转速环
(1)转速环截止频率

(2)电流环传递函数简化条件
(3)转速环小时间常数近似处理条件
3 系统仿真
3.1 仿真建模
在Matlab/Simulink中搭建基于动态数学模型的直流电机双闭环调速系统的仿真模型[6],如图1所示,再把上述计算得出的PI参数分别填入ASR和ACR模块。为了降低内环和外环反馈通道中的高频谐波引起的干扰,可分别在此处加入一阶惯性环节进行滤波,但滤波环节的加入必然会在反馈通道中产生一个短时间滞后,导致给定信号和反馈信号之间时间配合不一致,为此,再在ASR和ACR给定信号通道上加入一阶惯性环节进行时间同步,简化分析。图中给出的仿真模型为完整的模型,其中ASR和ACR为封装后的子系统,其内部已按照设计要求对各自的输出进行相应的积分限幅设计。

图1 基于动态数学模型的直流电机双闭环调速系统的仿真模型Fig.1 Simulation model of DC motor double closed-loop speed regulation system based on dynamic mathematical model
3.2 仿真分析
仿真算法选择ode23tb,仿真开始时间为0s,结束时间为7s,额定恒转矩负载用阶跃信号模拟,加入时间为4s时刻。仿真结果如图2所示。
在仿真模型中,为方便查看示波器曲线的数据,利用Workspace模块保存变量数据,查得转速响应曲线的峰值时间tp=2.43s,最大转速nmax=2635r/min,则转速超调量,和前面理论计算值非常接近,说明该仿真模型是合理的且符合设计要求。
另外,仿真结果图2表明,直流电机起动后,电枢电流Id立即上升到最大值Idm,并且保持Id=Idm不变,在Idm作用下电机转速n迅速上升,在此阶段ASR始终饱和,ACR保持PI调节作用。当转速n上升至给定值n*时,ASR的输入偏差为0,但由于ASR的积分饱和值仍然存在,故电机转速将出现超调,但超调量非常小。出现超调后,ASR的偏差为负,ASR迅速退饱和发挥PI调节作用,使转速稳定在2610r/min附近,从而实现了时间最优控制。另外,由图2和图3可知,在t=4s时加入额定负载,转速立即出现下降,但与此同时ASR的输出电流给定Ui*迅速增加,在ACR和ASR各自PI调节作用下,内环电流增加至与额定负载匹配,电机转速略微有所下降后又重新恢复稳定运行状态,表明系统转速波动小,抗扰能力强。

图2 转速、电流波形Fig. 2 Rotation speed and current waveform

图3 ASR输出波形Fig. 3 ASR output waveform
4 结语
按照典型工程设计方法设计双闭环直流调速系统,将内环设计成I型系统,将外环设计成II型系统。给出了基于动态数学模型的仿真模型,并按照工程设计确定的参数进行仿真,且仿真结果与理论分析一致,符合设计指标要求。转速电流双闭环直流调速系统能够实现时间最优控制,并且具备较好的起动、跟随性能,在实际应用中,具有重要的应用价值。

