基于积分图的非局部均值图像去噪技术研究

刘光宇 曾志勇 刘彪 赵恩铭 邢传玺

摘 要：由于传统非局部均值去噪技术不能合理地选取滤波参数，导致计算时间长，为了弥补该缺点，采用了一种基于积分图的非局部均值法用于图像的去噪仿真中。该方法将非局部均值与积分图相结合，降低计算量，提高计算效率。通过仿真实验表明，本文采用的方法拥有良好的去噪效果，并且相比传统的非局部均值去噪法计算效率更高。

关键词：去噪;非局部均值;相似性权重;积分图;计算效率

中图分类号：TP391  文献标识码：A  文章编号：1673-260X（2022）01-0022-05

1 引言

由于图像在采集、传输和加工的过程中受到噪声的影响，导致图像质量严重下降[1]，使图像变得模糊、不清晰，降低了图像的视觉效果。因此，去除图像中的噪声对于人们获取其中有效信息提供了必要的保障。图像去噪的关键是在去除噪声的同时尽可能多地保持原始图像的结构特征和细节特征[2]。为了减少噪声在图像传递和存储过程中的影响，需要对含噪图像进行去噪处理。图像去噪的目的是利用某种算法对图像进行处理，使图像尽可能地接近真实信息。因此，有效的图像去噪技术研究具有重要的现实意义。

1998年Tomasi等人提出双边滤波算法[3]，该算法以待去噪的像素点为中心，根据邻域像素与中心点的距离和与中心点在灰度的相似性赋予不同的权重，最后进行加权平均。由于双边滤波算法在确定权值大小时，考虑像素的空间距离和灰度距离，去噪效果好，但不能较好地保留纹理细节，并会出现“阶梯”效应[4]。2005年，Buades等学者[5]在双边滤波的基础上提出了非局部均值（Non-Local Means， NLM）去噪方法，该算法不再局限于局部去噪，而是根据该目标像素点为中心的图像块在全局图像中通过两个点的距离进行查找相仿图像块，根据相似性进行度量并赋予对应的权值，最后将所得到的所有相似像素权值相加再取平均。非局部均值去噪技术是针对图像像素的相似度权重和去噪性能进行研究分析[6]，通过对搜索窗口、邻域窗口的大小进行选取，并对相似性权重进行分析，选取最优的参数。对于每个像素的权值，采用以该像素为中心的图像块与以另一个像素为中心的图像块之间的高斯加权欧式距离进行计算[2]，根据图像的相似性对每一个像素点分配权重。非局部均值去噪技术可有效地提升去噪效果，保留图像边缘和细节信息[6]，但其具有计算复杂度高和相似性权值不能够精准确定等缺点[5]。为此，本文引用积分图[7]的概念，并将其应用于传统非局部均值去噪算法中。

2 非局部均值去噪技术

2.1 基本理论

传统非局部均值去噪技术[8-14]打破了以往的去噪方法的局部特性，将目标像素点的像素值计算延伸到整个图像区域。传统非局部均值去噪技术在计算时选取两个大小恒定不變的窗口，以某点周围的像素点组成的集合称为邻域窗口，用来搜索的区域称为搜索窗口。选取窗口后，将搜索到的图像块根据其相似性给该图像块的中心点像素给予相应的权重。该方法改变了以往比较单个像素点相似性的做法，将两个图像块进行相似性比较，更能有效地获取图像的结构信息。传统非局部均值去噪技术过程是以像素y为中心的像素块Ny放在搜索窗口中滑动，计算与另一个以x为中心的像素块Nx之间的相似性，最后将权值？棕（x，y）赋予Ny。

公式（5）由欧式距离d（x，y）和平滑参数h的比值决定了指数型加权核函数的衰减程度[5]。参数h控制指数函数的衰减速度，也影响滤波的程度和算法的去噪性能。根据噪声强度合理地设置h，便能达到良好的降噪效果。在图像平滑区域，图像的纹理较少，如果h的值较大，则说明该领域内的所有像素点的权值大小接近，在进行加权平均时，误差累积，会影响去噪图像像素灰度值的大小，当h趋于无穷大时，边缘保持较差，去噪性能越低。在细节区域，图像的纹理较多，存在相似像素个数较少，当h趋于无穷小时，有利于保持图像边缘的细节信息。f（x，y）会随着欧氏距离d（x，y）的增大而无限接近于0，欧氏距离d（x，y）与加权核函数f（x，y）的关系，即：

由图1知加权核函数[4]是一个单调减函数，其变化呈现为先快后慢。当d（x，y）数值较小时，权重值系数趋近于1，则图像块权重较大对运算过程影响较大，能够更快去除图像中的噪声，当取值较大时，则与之相反。

3 基于积分图的非局部均值去噪技术

3.1 基本理论

由于传统非局部均值算法计算量大，效率低。一种逐块估计的理论[16]被提出，该方法直接利用图像块与图像块之间的权值对所对应图像块内全部像素点同时进行滤波，即一次性计算出图像中所有点偏离该点坐标点方向的权重，而并非对某一点的所有偏离点进行逐一计算。积分图像常用于算法中，它能够降低算法的计算量，提高计算效率。

积分图的基本原理[10]是通过计算当前的图像和其中偏移后图像之间的欧氏距离，确定其权重值并平方，能将原有的图像相同尺寸的积分图计算得出，通过这样的积分图技术能将距离每个点具有偏移量的坐标点进行计算，只需计算一次原始图像就能获取任意区域的像素值和。引入积分图的非局部均值技术把偏移量作为最外层的循环，逐次把所有积分图求出来，每次在一个偏移方向上计算取得积分图。

式（14）中ux、uy分别为图像x和y的均值，？滓x、？滓y分别为图像x和y的标准差。C1=k1*L，C2=k2*L（其中k1=0.01，k2=0.03，L=255）。SSIM是衡量两幅图像相似度的指标，其值越大表明两幅图像越相似。

4 仿真实验

首先，选取一张大小为562x512的大理大学垃圾桶图像（图1）作为实验对象;对其添加均值为0，方差（VAR）分别为0.01、0.02、0.03、0.04和0.05的高斯白噪声;即可得相应的噪声图像（图2）;为了获取良好的降噪效果，需对垃圾桶进行仿真实验选取合适的平滑参数h，如表1所示;再采用NLM方法对含噪图像进行去噪处理，处理结果如图4所示。

由表1知选取平滑参数权值为5、8、10、20、30、40和50进行仿真实验。当选择h为5时，其PSNR的值为0.18656;当选择h为8时，其PSNR的值为0.11958;当选择h为10时，其PSNR的值为0.11981;当选择h为20时，其PSNR的值为0.11915;当选择h为30时，其PSNR的值为0.186;当选择h为40时，其PSNR的值为0.1829;当选择h为50时，其PSNR的值为0.1809。由式（11）知PSNR值越大说明去噪效果越好，所以仿真实验选择平滑参数为10。

从图3（a）（b）（c）（d）（e）可以看出，通过增加方差，图像中的高斯白噪声逐渐增多;圖4中对添加了高斯白噪声的图像经过非局部均值去噪技术处理后，图像中大部分高频噪声被滤除，图像变得清晰。由图4发现添加方差越大，去噪后的视觉效果越差;方差越小对图像的边缘和细节保留能力越强，去噪后图像更加清晰。从表2中的实验数据可以看出，方差为0.01时，MAE和MSE明显低于方差为0.02、0.03、0.04、0.05时的数值，表示其误差小，图像质量比方差为0.02、0.03、0.04、0.05时的图像质量好。PSNR和MSSIM是五个方差中对应该项实验数据中最大的，由式（11）（14）知，PSNR越大，图像失真越小;MSSIM越大，图像越相似，所以，当方差为0.01时，去噪后的视觉效果是最好的。

4.1 选取合适窗口尺寸

为了得出一个较好的结果，则需要对窗口尺寸做出选择，同时对相似性权重进行分析处理。本文选取了搜索窗口的大小为5x5，7x7，9x9，选取邻域窗口的大小为3x3，5x5，7x7。根据NLM算法的原理可知，邻域窗口是在搜索窗口内的，共有六组实验，即：

从表2中PSNR和时间数据结果知，邻域窗口3x3，搜索窗口5x5的PSNR值最大，时间最少;邻域窗口7x7，搜索窗口9x9的PSNR值最小，时间最长。由式（11）知PSNR值越大则说明图像失真越小;实验用时越少，计算复杂程度越小，计算效率越高。当搜索窗口大小为5x5，邻域窗口大小为3x3时，此时的实验后的视觉效果最好。

4.2 传统NLM技术与积分图的NLM技术实验结果对比

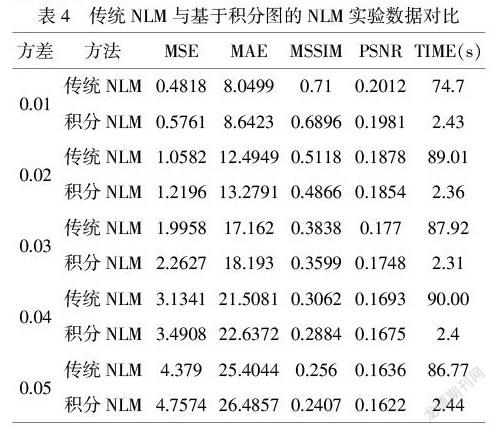
为进一步客观具体地评估所提出的方法，对图3中的含噪图像（Noisy image，NI）重复实验10次取平均值得出表3的数据。通过对两种去噪技术进行深入的比较与分析，进行Mtlab仿真。图5中直观图像对比两种去噪方法都显示了较好的去噪效果。通过表4数据发现，基于积分的NLM相比传统NLM在MSE和MAE数值有一定的提高，而MSSIM和PSNR有一定程度的降低，说明基于积分的NLM在同一方差情况下图像的保留和图像质量相对低一些。

从表4中可以明显发现，在五个等级方差中传统非局部均值去噪技术都比基于积分图改进的非局部均值去噪技术运行时间长。在对添加方差为0.01的含噪图像进行处理，所运行时间平均长达74.7s;基于积分图的非局部均值去噪技术处理图像耗时约2.43s，两者相差约30倍。在对添加方差为0.02的含噪图像进行处理，所运行时间平均长达89s;基于积分图的非局部均值去噪技术处理图像耗时约2.36s，两者相差约37倍。在对添加方差为0.03的含噪图像进行处理，所运行时间平均长达87.92s;基于积分图的非局部均值去噪技术处理图像耗时约2.31s，两者相差约38倍。在对添加方差为0.04的含噪图像进行处理，所运行时间平均长达90s;基于积分图的非局部均值去噪技术处理图像耗时约2.4s，两者相差约37倍。在对添加方差为0.05的含噪图像进行处理，所运行时间平均长达86.77s。基于积分图的非局部均值去噪技术处理图像耗时约2.44s，两者相差约35倍。通过实验数据对比明显说明基于积分的非局部均值去噪技术处理图像时间比传统非局部均值去噪技术处理图像时间更短，效率更高，更适合用于实时的图像处理中。

5 结论

本文为了弥补非局部均值去噪技术耗时长的缺点，在其算法中引入积分图的概念。基于积分图的非局部均值去噪技术把偏移量作为最外层的循环，逐次把所有积分图求出来，每次在一个偏移方向上计算取得积分图，减少运算量，减少计算时间。实验表明基于积分图的非局部均值去噪法与传统非局部均值去噪法相比在保持图像视觉效果的情况下所用时间更少，计算效率更高，在实时的图像处理中能够更好发挥作用。

参考文献：

〔1〕钱海明，孙金彦，王春林.基于非局部均值算法的图像去噪方法研究[J].安徽水利水电职业技术学院学报，2019，19（01）：7-9.

〔2〕单建华.改进权值函数的非局部均值去噪算法[J].中国图象图形学报，2012，17（10）：1227-1231.

〔3〕Tomasi C， Manduchi R. Bilateral filtering for gray and color images[C]//Iccv. 1998，98（01）：2.

〔4〕祝严刚，张桂梅.一种改进的非局部均值图像去噪算法[J].计算机工程与应用，2017，53（18）：192-198.

〔5〕Buades A， Coll B， Morel J M. A non-local algorithm for image denoising[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition（CVPR'05）.IEEE，2005，2：60-65.

〔6〕张书豪.一种改进权重的非局部均值滤波算法[J].信息通信，2017，26（05）：12-14.

〔7〕Viola P， Jones M.Rapid object detection using a boosted cascade of simple features[C]//Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition， 2001， CVPR 2001. IEEE， 2001， 1：511-518.

〔8〕Tasdizen Tolga. Principal neighborhood dictionaries for nonlocal means image denoising[J]. IEEE transactions on image processing： a publication of the IEEE Signal Processing Society，2009，18（12）.

〔9〕L. Zhang， L. Zhang， X. Mou， and D. Zhang. FSIM： a feature similarity index forimage quality assessment [J]. IEEE Transactions on Image Processing， 2011，20（12）： 2378-2386.

〔10〕Tasdizen Tolga. Principal neighborhood dictionaries for nonlocal means image denoising[J]. IEEE transactions on image processing： a publication of the IEEE Signal Processing Society， 2009，18（12）.

〔11〕Hua Z， Chen Y， Zhang X. A New Weight for Nonlocal Means Denoising Using Method Noise[J]. IEEE Signal Processing Letters， 2012， 19（08）：535-538.

〔12〕何春，宋國琴，郭科.一种改进的非局部均值去噪算法[J].西华师范大学学报（自然科学版），2020， 41（04）：421-428.

〔13〕徐翠婷，曹剑剑.基于NLM算法的加权核函数选取研究[J].现代计算机（专业版），2019，36（10）：68-70.

〔14〕刘晓明，田雨，何徽，仲元红.一种改进的非局部均值图像去噪算法[J].计算机工程，2012，38（04）：199-201+207.

〔15〕张娜，刘辉，尚振宏，邹滨益.改进权重函数的非局部均值图像去噪算法[J].计算机工程，2016，42（12）：254-261.

〔16〕M. Lindenbaum， M. Fischer， and A. Bruckstein. On Gabor’s contribution toimage enhancement [J]. Pattern Recognition， 1994， 27（01）： 1-8.

〔17〕侯春萍，李浩，岳广辉.局部和全局特征融合的色调映射图像质量评价[J].湖南大学学报（自然科学版），2019，46（08）：132-140.