浅谈高等数学课程思政的教学设计——以“梯度”为例

马 雷

（上海理工大学理学院，上海 200093）

本论文研究的内容是课程思政下高等数学的教学设计。在以往的文献中，例如参考文献[2][4]，均是对课程思政与高等数学进行系统的阐述。而本文则是从高等数学中选出具体的一节来进行教学设计。教学设计是服务于教学的，它融合了教学的理论和课程思政的价值观，运用系统的方法明确教学目标，建立教学过程中的教学方案。同时也为教师自己提高教学效率，完善教学过程打下基础。如何在课堂教学中将思政相关内容进行融合呢？在课堂教学中，主要是利用高等数学的特点向学生传达课程思政，在传授知识的同时也能对学生进行思想政治教育。这不仅能够向学生灌输知识而且能够真正做到“授人以渔”。以高等数学的课程为载体，培养学生明辨是非的能力和勤奋学习的习惯，坚定学生的政治信仰。将社会主义核心价值观有效的、全面的、传达给学生，使学生全面发展，为学生后续的学习和事业提供基础，并使其成为实现中华民族伟大复兴的践行者。本文将以高等数学中的梯度[5]内容为基础，积极地将高数的相关知识与课程思政相关联。结合高等数学的特点系统化的完善教学设计，推动相关理论研究的发展，同时能够对教案设计，教学大纲等教学活动产生指导意义。

梯度是高等数学中非常重要的概念，同时也是整个课程中的重点和难点。课程主要目的就是通过对梯度课程的讲授，帮助学生掌握梯度的概念和计算，理解梯度的意义和应用。本次课程大致分为三个部分。（1）梯度的定义。通过对爬山问题的介绍来激发学生的思考，吸引学生的注意力，同时也能和学生产生更多的互动，有比较好的课堂氛围从而使得学生的学习达到事半功倍的效果。（2）梯度的等值线。先通过 PPT等图片的方式形象地向学生展示等值线，从而给出等值线严格的数学定义，并且介绍几个简单的例题来加强同学对梯度和等值线的理解。（3）内容小结。引导学生直观上理解梯度的概念和意义，掌握梯度和方向导数的关系，并将梯度进一步拓展至后续课程中（机器学习，最优化理论）的应用。在总结的最后部分，也要让学生们意识到和掌握一定的学习方法，从而培养学生分析问题和解决实际问题的能力。同时透过这样的课程设计也能够让学生更好地对梯度相关知识进行了解及掌握，更好地进行教育的同时，也能更加明确我们学习的意义。

同时可以转变授课方式，变更多的行为开展研讨与交流，能够将高数问题从课堂教学和课程发展育人的角度进行解读设计，将高等数学的育人功能更好的呈现，扩展育人的路径与视野，通过这样的设计也可以为高等数学类课程思政建设提供新方法与新思路。本文结合参考文献[1][3]给出具体的教学安排：

1 爬山问题的引入

顾名思义，爬山问题就是当你在山脚时，如何最快地爬到山顶？这是我们现实生活中比较常见的问题。本次课堂先从通俗易懂的身边事例开始授课，让同学们带着思考进行后面的学习。数学上描述爬山问题：设函数是山的高度，沿着哪个方向会最快的到达最高点？为了回答这个问题，我们继续学习后面的内容。

2 梯度的定义

2.1 方向导数

首先回顾偏导数的有关内容，从定义出发延伸出方向导数的定义。设函数 在点 处存在偏导数，方向的方向角是 。存在下列极限

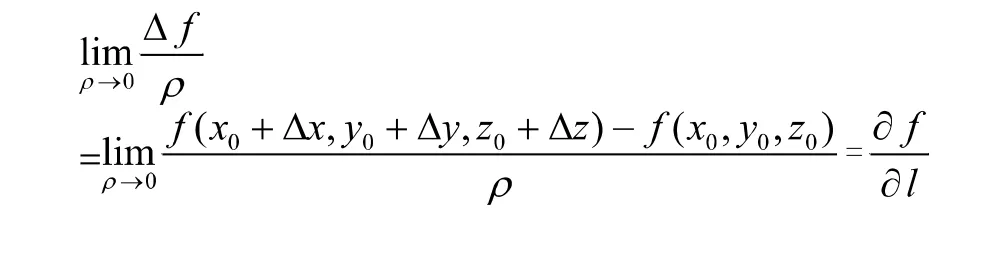
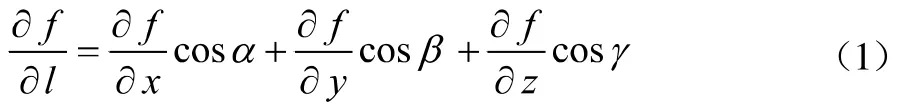
这一部分是方向导数的授课内容，其相关的证明细节和具体内容会通过板书的形式呈现给大家。向同学们介绍方向导数的同时，要举例说明函数在一点可微只是方向导数存在的充分条件而不是必要条件；同时函数在某点处的连续也不是方向导数存在的必要条件。在介绍完方向导数后，我们发现方向导数是两个向量点乘的结果。通过这一观察，我接着介绍梯度的定义并且梯度与方向导数的联系。

2.2 梯度

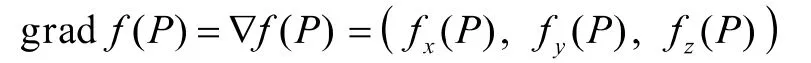
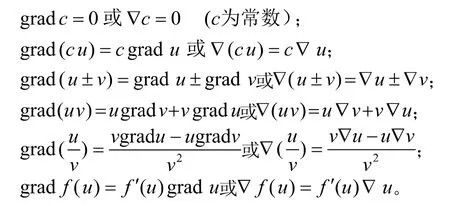
上述公式是要求学生必须掌握的。

课堂进行到这里，授课人将会列举几个实际例题向同学们具体讲解方向导数和梯度的计算，同时向学生提问如何将方向导数与梯度联系起来，让同学们带着思考进入后面的课堂教学。为了将二者之间的关系更好地呈现给同学，这里将会通过图片或者动画来辅助教学。这也能使同学们对二者的概念有更直观的印象，从而得到更好的教学效果。

公式（2）表明函数的方向导数为梯度在该方向上的投影。由此可以推出当方向一致时，方向导数取得最大值，此时对应的方向即是梯度方向。这也就回答了最初的爬山问题，沿着梯度的方向向上爬可以最快地爬到山顶。

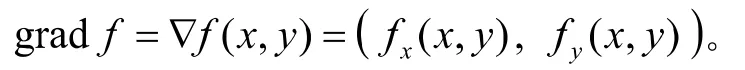
3 梯度的应用和意义

3.1 等值线

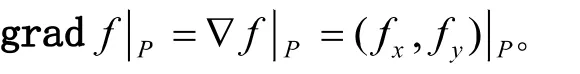
解释：函数在某一点的梯度垂直于该点的等值线，指向函数增大的方向。等高线图举例。例1：通过matlab等数学软件将例1中的函数等高线画出，向同学们展示等高线的图示效果并且描述等高线的特性（同一等高线高度相同；闭合曲线）。

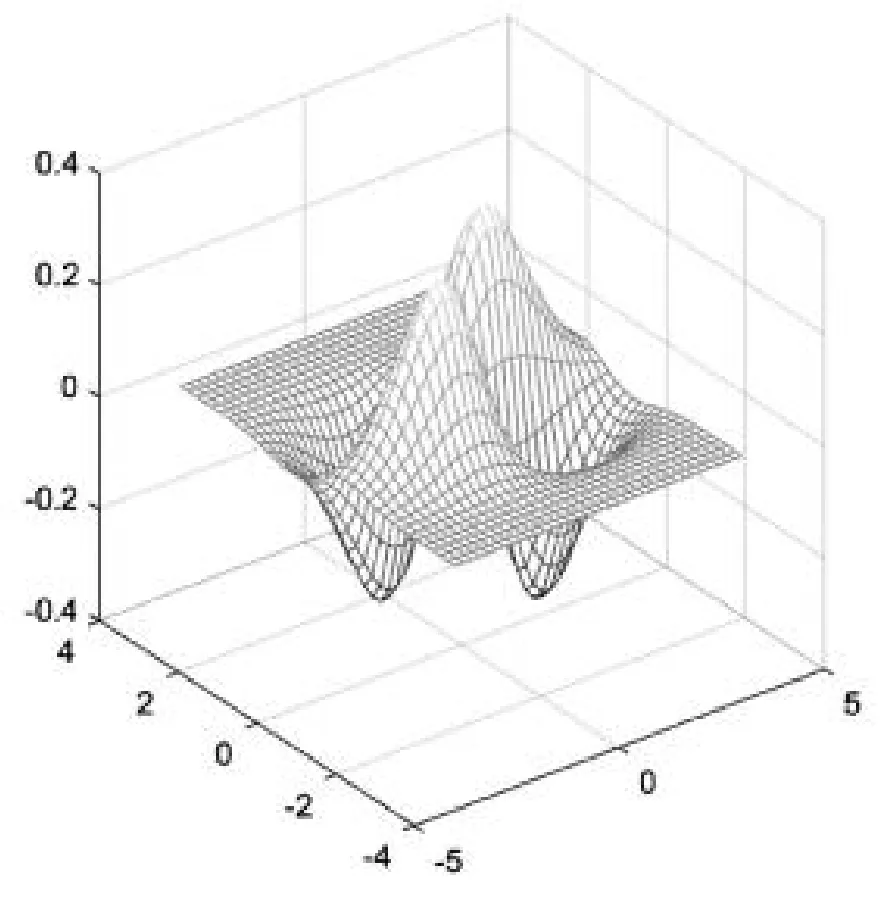
图1 的图像

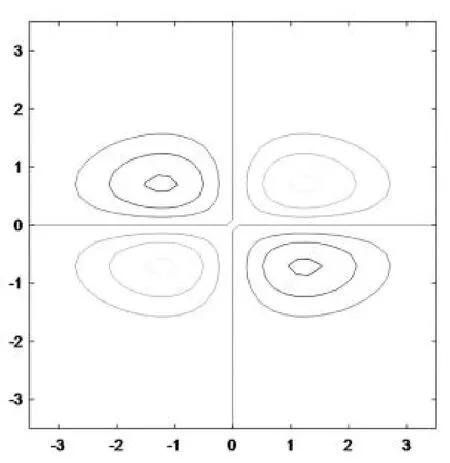
图2 的等高线

另一方面，从等高线的走势图，我们可以与思政内容相结合。等高线的高度比喻为人生的高峰与低谷。正是这一圈圈形象又具体的图案从不同的角度揭示了人生的丰富多彩。高峰时，我们将心怀感恩，不忘初心，勇于攀登下一个制高点。低谷时，我们也不必自暴自弃，调整心态重新出发，努力活出自己的精彩。

3.2 物理意义（场论的初步）

梯度是一个向量场，由此我们可以简单引入场的概念。场是物理和数学等学科中非常重要的一个概念。在我们的日常生活中接触到的温度，密度，电势都可以理解为数量场。在引入空间的直角坐标系之后，空间的每个位置均可以用坐标表示，因此此时给定某个函数就相当于给了一个数量场。设点集，函数，则称f是D的一个数量场。同理还可以定义向量场。如果，则称F是D的一个向量场。比较常见的是速度场。场论揭示了更加深刻的数学思想。对场论的初步学习，将有助于学生系统地掌握方向导数和梯度的基本理论，同时也能激起同学们对未来课程的学习兴趣。

4 内容小结

本文利用高等数学中梯度这一节的内容作为实例完成了融入课程思政元素的教学设计。从教学大纲出发，不仅完成了课程的教学要求，同时也突出了教学重点和难点。以爬山问题作为切入点，引发学生思考，激发学生的学习兴趣。课堂教学中多次运用动画的效果直观地将抽象的方向导数和梯度概念介绍给学生。这也对学生的学习效果有良好的促进作用。

通过这样一次基础的课程设计，教会学生辩证的思考以解决实际数学问题，帮助学生们从实际生活角度出发，通过对生活的观察，真正学习和掌握到高等数学与生活的联系，这实际上也是复杂问题与简单问题之间的转换。不仅仅教会学生们学习数学知识，而且也能让同学意识到这也是实践与认识的一个循环。