平面运动学的欧拉公式描述和分析
郑拯宇
(重庆理工大学 机械工程学院,重庆 400054)
平面运动学是通过定义各运动要素之间的关系来描述研究对象的机械运动规律.由于相对性是机械运动的重要特征之一,因此在不同参考系下对同一研究对象所表现出的运动特征(或规律)是不同的;并且,用以描述机械运动规律的相关运动特征参数(角速度、角加速度等)是带有方向性的,具有矢量形式.这就需要在各参考系下对这些运动特征参数进行繁琐的矢量描述和分析,并确定不同参考系下各矢量之间的转换关系.研究表明:国内外现代理论力学教材普遍系统地采用了矢量记号[1],尤其在平面运动学问题的描述和分析上主要是采用矢量分析法进行的[2-4].但现有教材中的矢量分析法的推导过程较为繁琐,不易理解.并且,由于理论力学教材中相关概念并不十分准确和完整,尤其是对于点的运动合成定理中相对位移、相对速度、相对加速度等概念的描述存在一定的歧义[5,6],从而使得平面运动学长期以来一直成为理论力学教学实践活动中的难点和探讨热点[7-10].鉴于此,一些学者试图利用复变函数的某些性质来解决平面运动学的部分问题,并进行了有益的探索[11-13],但其推衍过程仍显繁琐和不足.
本文将复变函数领域中的欧拉公式引入平面运动学中,全面描述并分析了平面运动学中的相关问题.由于复平面概念将复数与矢量紧密联系起来,其中的复数四则运算规则为确定不同参考系下各矢量之间的转换关系提供了方法与规则,而欧拉公式的引入则为复数的四则运算带来了简洁和规范.
1 平面动点的复平面描述
1.1 欧拉公式
莱昂哈德·欧拉(Leonhard Euler)所建立的欧拉公式将复数、指数函数与三角函数联系了起来,从而使得三角函数的定义域扩大到复平面领域[14]:
eiφ=cosφ+isinφ
(1)
其中:e是自然常数,i是虚数单位,φ是以弧度为单位的参数,这里取逆时针为正值.
eξ是沿径矢方向的单位矢量,横向单位矢量垂直径矢方向且与φ增大方向一致,易知eξ与eη之间的关系可用下式表示:
(2)
eη垂直于eξ,即方向沿eξ逆时针旋转π/2度.
利用数学变换,可知
(3)
可见,复指数形式的欧拉公式的引入为复平面领域的矢量计算提供了一套简洁规范的运算规则.同时,由于复数对于四则运算是封闭的,这为利用欧拉公式研究矢量在复平面的旋转变换和平移条件下的变换带来可能.
1.2 平面点的描述
平面上任一动点M的运动均可建立相应的复平面并引入欧拉公式对其径矢的变化进行描述(如图1所示).则动点M的运动方程可用如下形式描述:

图1 复数平面中的欧拉公式
rM(t)=|rOM(t)|[cosφ(t)+isinφ(t)]=rOMeiφ
(4)
2 平面运动学分析
2.1 点的运动描述
现假设复平面上动点M的矢径r末端描绘出一条连续的矢端曲线(即动点M的运动轨迹),动点在Δt时间段从M点沿轨迹移动至M′点,如图2所示.

图2 动点M的运动轨迹
动点M的速度可表示为
(5)
将式(5)对时间求二次导数,则可得到动点M的加速度:
(6)
可见,动点M的运动参数随时间的变化规律体现在矢径方向eξ以及垂直矢径的方向eη上.由于上式包含了矢径的模rOM(t)对时间的一阶和二阶导数,这将对于诸如点的螺旋运动等变径矢运动状态的理解和分析带来便利.
若动点M的运动轨迹已知,则可以在复平面上采用瞬时坐标系的概念:即选取动点轨迹上任意瞬时M点处的曲率中心为瞬时复平面的原点O.则动点M的矢径可表示为
r(t)=ρeiφ′(t)
(7)
这里,ρ为动点轨迹上该瞬时M点处的曲率半径,为常量;φ′(t)是轨迹上该瞬时点的曲率中心方向与水平轴的夹角.
将上式代入式(5)和式(6),则可轻易地推导出动点M的经典弧坐标形式:
(8)
其中,eτ=ieiφ′(t)是动点轨迹上t时刻M点处的切向单位矢量;en=eiφ′(t)是其法向单位矢量(如图2所示).
2.2 点的合成运动
由于相对性是机械运动的重要特征之一,因此对于平面上点的复杂运动,一般需要建立定系和动系以便直观描述动点的运动.为了研究动点M的合成运动,分别以点O和点O′为原点建立定复平面(定系)和动复平面(动系),如图3所示.其中,单位向量:eξ=ei(θ+φ),eη=iei(θ+φ).
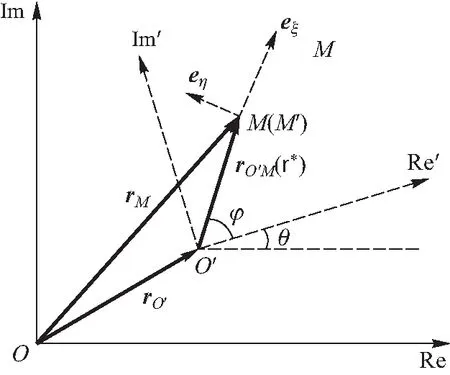
图3 点的合成运动
则动点M的矢径可描述为
rM=rO′+rO′M=rO′+rO′Mei(θ+φ)
(9)
将式(9)两端对时间求导,可得动点M的绝对速度和绝对加速度:
(10)

若动复平面上动点相对运动轨迹已知,则可采用瞬时坐标系概念,并结合式(5)、式(6)和式(8),则可得到所熟悉的经典相对速度和相对加速度的表示形式[16,17]:
(11)
2.3 刚体的运动分析
刚体是各质点间的相对位置保持不变的特殊质点系,同样需要建立定系和固结于刚体的动系来直观描述刚体上点的运动.因此,刚体运动的分析可归属于特殊情况下点的合成运动分析,其核心仍是本文所推导出的式(10).所不同的是:需根据刚体运动情况(平行移动、定轴转动和平面运动)对公式中所出现的各参数(rO′、rO′M、φ、θ)是否为变量进行必要的设定和说明.
1) 刚体的平行移动
若刚体在平面上作平行移动,则选取刚体上某点O′为动复平面的原点,建立随刚体平移的动复平面,如图4所示.

图4 刚体的平行移动
刚体上任一点M的矢径rM均可表示如下:
rM=rO′+rO′M=rO′+rO′Meiφ
(12)
这里,rO′M=常量;φ=常量;rO′=矢变量.
现将式(12)代入式(10)(此时刚体作平移,θ=0,可得到点动点M的速度及加速度:
(13)
上式表明:对于平行移动刚体,其上所有点的速度以及加速度均是相同的,故可以用刚体上任一点的运动代表整个刚体的运动.
2) 刚体的定轴转动
设平面上某刚体绕其通过转动中心O′的轴进行定轴转动,则选取转动中心O′为原点建立随刚体定轴转动的动复平面,M为刚体上任一点,如图5所示.

图5 刚体的定轴转动
动点M的径矢可表示为
rM=rO′+rO′M=rO′+rO′Mei(θ+φ)
(14)
这里,rO′=常矢量;rO′M=常量;φ=常量;θ=变量;法向和切向单位矢分别为:en=ei(θ+φ),et=iei(θ+φ).
将式(14)代入式(10),则得到点M的绝对速度和绝对加速度:
(15)
3) 刚体的平面运动
若刚体作平面运动,则在刚体上选取一点O′作为原点(基点)建立动复平面,M为刚体上任意点,如图6所示.

图6 刚体的一般平面运动
动点M的矢径可描述为
rM=rO′+rO′M=rO′+rO′Mei(θ+φ)
(16)
这里,rO′=变矢量;rO′M=常量;φ=常量;θ=变量.
将式(16)代入式(10).可知:
(17)

3 结论
本文采用复函数平面以代替传统的Ox、Oy轴实数平面,利用复数与向量的对应关系,并引入以复指数形式表达的欧拉公式,其封闭的四则运算公式为理论力学中的平面运动学问题的矢量分析与计算提供了一套规范的运算规则,避免了实数平面矢量分析中的点积和叉积运算规则所带来的困惑,从而使得平面运动学的分析与计算变得简洁和规范.由于整个平面运动学分析是建立在复函数平面上的,因此只需要关注动点、基点(参考点)在复平面(含定、动复平面)的矢量表达,并转换成相应的欧拉公式复指数形式,利用速度和加速度的定义并结合复指数的运算规则,可快速地获得动点完整的速度和加速度.在已知动点轨迹的前提下,引入瞬时坐标系的概念,则所得到的平面运动学问题(刚体的运动、点的合成运动)中的速度和加速度与经典理论完全一致.

