基于编码器-解码器的离线手写数学公式识别

杜永涛，余元辉

(集美大学计算机工程学院，福建 厦门 361021)

0 引言

手写数学公式识别可分为两种类型：在线手写数学公式识别和离线手写数学公式识别[1]。在线识别处理的是触摸屏设备中笔迹的点序列数学公式，而离线识别处理的是静态数学图像。由于公式图像比计算机视觉中的普通图像包含更复杂的二维结构和空间关系，离线手写数学表达式识别通常被认为比在线手写数学表达式识别困难得多。

已有许多与离线手写数学公式识别相关的方法[2-8]。这些方法大致可以分为两类：基于语法的和基于编解码器的。基于语法的方法通常由三部分组成：符号分割、符号识别和结构分析[9]。Lee等[3]提出了一个手写数学公式识别系统，系统的笔画分割采用分割连通域的方法将公式分割成若干部分，单符号识别采用预训练的分类器对分割符号进行分类识别，但该系统只对公式结构中根式、分式和上下标三种类型的结构可以有效识别，不能识别其他公式结构。Okamoto等[4]提出两种手写数学公式识别方法，一种是依据字符投影的轮廓信息进行笔画分割，然后使用模板匹配法进行单符号识别的顺序解决方法，另一种是采用自顶向下和自底向上结构分析的全局解决方法。这类基于语法的传统方法需要依赖大量的数学公式语法知识，只能针对某些场景，泛用性不强，且在大数据集中不能受益。Zhang等[5]首次提出了一种基于编码器-解码器结构的WAP模型来解决离线手写数学公式识别问题，该模型能够自动学习数学公式语法和处理符号切分，并通过注意力机制解决对齐问题。Wu等[6-7]为了克服写作风格的变化，提出了结合深度学习和对抗学习的PAL模型和PAL-v2模型，其中PAL-v2模型采用基于卷积神经网络的解码器解决了循环神经网络中的梯度消失和梯度爆炸的问题。Le等[8]提出了基于注意力的编码器-解码器系统的数据生成策略，通过数据增强的方式证明了附加生成数据具有优越性。Anh[2]结合手写数学公式和印刷体数学公式特点，提出了一种双重损失注意法用于手写数学公式识别。然而，这些基于编解码器的方法没有充分结合手写数学公式中的尺度变化情况，会出现解析不足的情况，同时缺乏对长公式序列建模，对复杂数学公式结构更加解析不足。

基于此，本文在传统编码器-解码器模型基础上进行了改进，以多尺度密集卷积神经网络作为编码器提取多分辨率特征，用Transformer模型替代RNN模型作为解码器进行长公式序列建模，同时设计了两种相对位置编码方式嵌入图像位置信息和LaTeX符号位置信息。

1 网络模型

本文提出的编码器-解码器模型如图1所示。

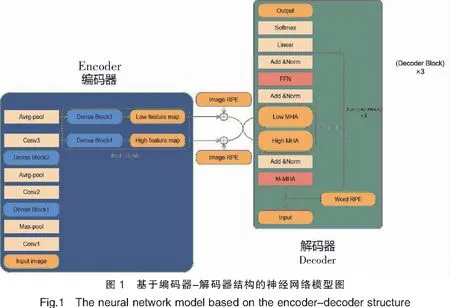
1.1 编码器

本研究在密集卷积神经网络(DenseNet)的基础上进行了编码器的改进。DenseNet[10]由黄高于2017年提出，它的主要思想是通过在每一层和所有后续层之间建立密集连接来促进层与层之间的信息交换。第l层的输出特征为:

x1=H((x0;x1；…；xi-1))。

(1)

其中:(x0;x1；…；xi-1)表示所有输出特征的串联操作;Hi(·)表示三个连续层的复合函数——批量标准化(BN)层[11]、ReLU层[12]和3×3卷积(Conv)层。通过通道维度的级联操作，DenseNet能够更好地传播梯度。

为了进一步提取输入图像的多尺度特征，本研究在DenseNet的基础上增加了多尺度结构。如图1所示，编码器采用的多尺度DenseNet包含了4个密集块(DenseBlock)，每个密集块都使用瓶颈层来提高计算效率，即在每个(3×3)卷积之前引入(1×1)卷积，以减少特征图的输入。在进入第一个密集块之前先对输入图像进行核大小为(7×7)、步长为(2×2)的卷积操作，然后进行核大小为(2×2)、步长为(2×2)的最大池化层操作。使用核大小和步长都是(1×1)的卷积以及核大小和步长都是(2×2)的平均池化作为第一和第二密集块与第二和第三密集块之间的过渡层，该过渡层将每个块的特征图的数量和大小减少一半。第二和第四密集块之间只使用核大小和步长都是(1×1)的卷积作为过渡层，该过渡层只将第二个密集块的特征图数量减少一半，而特征图大小不变。第三和第四密集块后输出特征图大小不同，两个分支经过(1×1)卷积层降低图像特征图数量，同时统一两个分支的特征图数量。最后两个分支输出特征分别作为多尺度DenseNet模型的高分辨率特征和低分辨率特征。低分辨率特征可以捕获更大的感受视野，高分辨率特征可以捕获更细粒度的视觉信息。

1.2 解码器

Transformer[13]是一个完全基于注意机制的神经网络架构。相比于传统解码器的循环神经网络(RNN)[14]，其内部的自注意机制从根本上解决了RNN的梯度消失问题，同时还能通过多头机制实现良好的并行化训练，大量节约训练时间。本文采用的Transformer解码器如图1所示，每个解码器模块(decoder block)由四个部分组成。

2)MS-MHA，多尺度多头注意力模块。该模块采用两个不同维度的多头注意力层构成，其计算公式为：Zl=MultiHeadl(Q,K,V)，Zh=MultiHeadh(Q,K,V)。其中的K、V是编码器输出的低分辨率特征编码矩阵；Q是输出矩阵。

3)Add&Norm，由残差连接和归一化两部分组成。计算公式为：LayerNorm(X=F(X)),其中F(·)表示X经过M-MHA、MS-MHA或者FFN模块的函数转换。

4)FFN，一个两层的全连接层。第一层的激活函数为Relu，第二层不使用激活函数。其计算公式为：FNN=(X)=max(0，XW1+b1)W2+b2。

1.3 相对位置编码

图像特征和词向量的位置信息可以有效地帮助模型识别需要关注的区域。本文使用图像位置编码和词向量位置编码两种编码方式，在编码器和解码器嵌入图像特征位置信息和词向量位置信息。

1.3.1 词向量相对位置编码

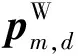
其中θi=10 000-2i/d，i表示维数下标。

1.3.2 二维图像相对位置编码

(2)

(3)

对于每个二维图像像素点坐标(x,y)，通过公式(2)先对其进行归一化，然后分别对二维归一化位置进行旋转式位置编码，最后将它们连接在一起。

2 训练和预测

2.1 训练

在图像x和模型参数θ的条件下，传统的自回归模型概率分布可以表示为：p(yj|y1,K,yj-1,x,θ)。其中j为目标序列中的索引。

2.2 预测

与训练过程不同，模型在预测过程中没有目标LaTeX 序列真实标签输入，因此只能根据上一个LaTeX预测符号预测下一个LaTeX符号，直到结束符号出现或达到预定义的最大长度。对此，为了生成全局最优LaTeX序列，本研究采用波束搜索算法[18]在每个时间步生成多个候选的输出序列，最终选择最优的LaTeX序列。

3 实验结果与分析

3.1 实验环境

实验模型均基于云服务器深度学习环境下进行部署。云服务器环境配置单块NVIDIA Tesla V100 32 GB显卡，基于Linux操作系统搭建PyTorch深度学习平台，其中CUDA版本为11.0，cuDNN版本为8.0，Python版本为3.7，PyTorch版本为1.7。

3.2 数据集

本文使用的数据集是CROHME 2014。它的训练集包含8836个手写数学公式，测试集包含986个手写数学公式。每个手写数学公式样本单独保存在一个InkML文件中，其中包含了笔迹信息、符号级别的标签信息、表达式级别的标签信息、书写人的相关信息、笔迹标识信息等。本文先将InkML文件中的笔迹信息转换为离线手写数学公式图像用于训练和测试，离线手写数学公式图像如图2所示。

3.3 评价指标

为了测量本系统的性能，使用字错误率(RW)和公式识别准确率(RE)作为度量标准。公式表示为：RW=(Nsub+Ndet+Nins)/NY,RE=NCOR/Y。其中：Nsub、Ndet、Nins是取代、缺失和插入的LaTeX公式符号数量；NY是LaTeX公式训练集中的符号数；NCOR是正确识别的LaTeX公式数量；Y是LaTeX公式训练集中的公式数量。

3.4 实验结果

CROHME 2014数据集上一些模型的结果如表1所示。为了确保性能比较的公平性，各方法都只使用官方提供的8836个培训样本，没有使用数据扩充。本研究以WAP模型[5]作为基准模型，首次采用编码器-解码器结构，其中编码器基于全卷积网络模型，解码器基于RNN模型。与其他方法相比，本模型明显优于WAP[5]、End-to-End[8]、PAL-v2[7]和Dual Loss Attention Network[2]。

表1 本模型与其他四种模型的比较结果

本模型采用双向语言建模方法替代单向语言建模方法，同时用Transformer模型解码器替代RNN的解码器，不采用额外的印刷体数学公式图像进行训练，获得了15.03%的公式识别准确率提升。PAL-v2模型采用了统计语言模型作为后处理(本模型不采用任何后处理)，公式识别准确率提高了6.55%。Dual Loss Attention Network模型采用手写数学公式图像和印刷体数学公式图像结合的双重损失注意网络，字错误率降低了1.41%，公式识别准确率提高了3.55%。

表2显示了中多尺度结构(muti-scale)、相对位置编码(RPE)、双向语言建模(bi-trained)以及波束搜索算法(beam search)对字错误率和公式识别准确率的影响。从表2中可以看出，以标准密集卷积神经网络(DenseNet)作为编码器的基准模型，多尺度结构训练模型在公式识别正确率上提升了约2.25%，表明多尺度结构有助于模型捕捉图像中不同尺度的图像特征信息;相对位置编码约提升公式识别正确率3.91%，表明嵌入图像特征位置信息和词向量位置信息有效提高了模型的泛化能力;双向语言建模在公式识别准确率上也比单向语言建模方法训练的模型高出约2.49%，表明双向语言建模方法有助于克服单向语言建模方法不平衡输出的问题，提高模型泛化能力。此外，采用波束搜索算法对解码结果进行评估也使公式识别正确率提高了约1.65%，表明波束搜索算法有助于生成最优LaTeX序列。

表2 CROHME 2014测试集的消融实验

图 3 展示了本模型的几个识别示例。从图3可以看出，对于数学公式中的上下标、括号、求和、极限、积分、分式、根式等结构，本模型成功学习到了这些数学公式结构语法。通常情况下，这些公式结构都会被保留下来，但会有一两个符号识别错误。这些符号识别的错误主要来自于手写数学符号的模糊性引起的歧义。

图 4展示了几个错误识别的例子，从中可以看出大写字母与小写字母、字母与数字之间的相似性会给模型识别带来困难，比如公式“S/V”和“-P(V1-V1)”中就将大写字母“V”和“P”识别成了小写字母“v”和“p”，公式“60o”中将符号“°”识别成了数字“0”。同时对于一些由英文字母构成的特殊运算符号，模型将难以区分特殊运算符号和英文字符，比如公式“cos 2α”中将“cos”识别成了“c”、“0”、“5”。

4 结语

本文的主要工作是针对离线手写数学公式识别任务提出了一种新的编码器-解码器模型。用多尺度密集卷积神经网络作为编码器对手写数学公式图像进行多分辨率特征提取；用Transformer模型替代传统RNN模型作为解码器解码预测手写数学公式图像的LaTeX序列；通过两种相对位置编码，可以捕获图像特征位置信息和词向量位置信息，帮助模型关注有效的图像区域。实验结果表明，本文提出的模型在CROHME 2014数据集上取得了55.43%的公式识别准确率和10.75%的字错误率，相比于当前最先进的Dual Loss Attention Network方法[2]，公式识别准确率提高了3.55%，字错误率降低了1.41%，证明了所提出模型的有效性。在接下来的研究工作中，提升模型在多层嵌套结构和区分相似符号的数学公式上的识别准确率仍需进一步探索。