壁面电荷对铜表面冰黏附的影响研究

蔡文豪，许雄文，2

（1 华南理工大学电力学院，广东 广州 510640； 2 广东省能源高效清洁利用重点实验室，广东 广州 510640）

引 言

过冷水式动态冰蓄冷技术制备具有相变潜热的冰浆作为储能介质，具有高能量密度的特点，且制备系统简单，传热效率高[1]。然而该方法面临的一个问题就是所形成的冰晶极易黏附在低温换热表面[2]，降低系统的换热效率，甚至引发堵塞流道的问题。目前常采用的解决方案是提高过冷水的流速[3-4]，利用流体扰动产生的分离效果剥离过冷壁面上的黏附冰，但大大增加了水泵功耗。减小冰与壁面之间的黏附强度[5-7]是降低过冷水流速的有效途径，因此有必要分析固体表面冰的脱附机制，找到减小冰黏附强度的有效方法。另外，冰黏附在固体表面还会对很多工业运行安全造成威胁。如风机叶片和光伏面板上附冰会降低可再生能源基础设施的性能[8]，热泵翅片结霜会影响制冷设备的稳定运行[9]，机翼附冰会威胁航空安全[10]，等等。因此减小冰与壁面之间的黏附强度研究具有很好的科学和工程意义。

冰在自然状态下最常见的是六角形形态，根据Bernal-Fowler 冰规则[11]，每个水分子必须接受和提供两个氢键，才能维持规则的冰晶体结构，然而对处于界面区域的水分子来说，这显然是不可能的，其结构必然会由于两侧的受力不同以及固体壁面无法提供氢键而发生重构，形成定向非随机无序的结构，使该层中水分子具有可移动性，最终导致该层黏度与液态水相当，称为准液体层[12]。准液体层已被一系列实验证明存在，并在剪切和剥离过程中具有润滑作用。为了降低表面黏附，人们利用这一特性，将与水不互溶的润滑剂注入多孔表面(slippery liquid-infused porous surface，SLIPS)[13]或保持在粗糙纳米结构表面涂层[14-16]中，使固体表面结冰时，润滑剂能填充到冰和固体表面之间，降低冰的黏附强度，从而实现冰的自然力（例如风、重力和振动）去除[17]。一些设计力求获得真正的准液体层而非使用润滑剂。它们采用高吸水性涂层[18]、吸湿性聚合物[19]、水合性聚合物[20]以及聚电解质涂层[21]，利用高的吸水性和水合作用在壁面区域形成并维持较厚的准液体层，以减小冰的黏附强度。相当于通过表面处理来保持比原有状态下更厚的准液体层来实现低黏附强度的目的，这种采用润滑层来促进黏附冰脱附的策略在实际应用中具有很好的应用前景[22-23]。

在动态蓄冰的换热过程中，流体的剥蚀力较小，重力和振动基本可忽略，对于冰的脱附要求更高。因此，希望通过其他物理手段来增加准液体层厚度并减小冰的黏附力。固体表面荷电，可以改变近壁面水分子的偶极方向，从而改变水的结冰过程。在带电Pt（qPt=0.12 e，1e=1.6×10-19C）纳米通道中，吸附在带电表面的水分子之间会形成一个二维的氢键网络，干扰水分子层之间的氢键形成，最终导致壁面附近无法结冰，且冰在接近表面时生长速度减慢[24]。在带电石墨烯上的水覆盖层会随着碳原子携带电荷量（qC=0～0.18 e）的增加依次经历冰到液体和液体到冰的转变[25]。因此壁面荷电有望增加准液体层厚度。由于准液体层厚度在纳米尺度，为了验证这个想法，需要进行低于冰点的水分子体系的分子动力学模拟实验。

分子动力学模拟凭借其原子级别的分辨率在准液体层的模拟中占有一席之地[12,26]。对于黏附冰脱附的行为，分子动力学模拟包含了模拟空间中所有的力学关系，可以方便地导出固体壁面对冰块的黏附力。Xiao 等[27]在原子尺度上完成了冰黏附力学的分子动力学研究，并且给定准液体层厚度，研究了硅表面和石墨烯表面准液体层的存在对冰黏附强度和剪切强度的润滑作用。然而人为给定的液层厚度无法反映准液体层对外界环境的依赖性。Afshar等[28-29]改进了上述不足，他们使用全原子分子动力学模拟，分析了平衡后冰块的静态结构，关注了不同温度下准液体层的厚度变化，并研究了表面粗糙度和温度对石墨衬底上的冰黏附强度和剪切强度的影响，相对全面地在原子层面解释了冰的脱附机理。

本文拟在两铜壁面之间构建纳米尺寸的冰立方模型，采用铜板原子静态和脉冲荷电的方式来改变原有的准液体层厚度，通过对水分子施加垂直于壁面且大小一定的拉力，使得冰块恰好脱离壁面，以测定其黏附强度。本研究拟量化同一温度不同壁面荷电量时的准液体层厚度及其对应的冰黏附强度，以期提出减小冰黏附强度的有效方法。

1 模型和模拟

1.1 水分子-铜壁面体系模型

1.1.1 模拟参数 本研究采用分子动力学软件LAMMPS[30]进行纳米尺寸冰块脱附的模拟，采用数据可视化软件OVITO[31]观察冰块的平衡情况。冰块的建模采用TIP4P/ICE[32]刚性非极化水模型，因为该模型产生的六角形冰的熔点为272.2 K，密度为0.909 g/cm3（250.0 K，1 bar，1 bar=0.1 MPa），能够很好还原水的固液相图，其模型参数见表1。在模拟过程中使用 SHAKE 算法[33]固定 H—O 键的键长以及H—O—H 的键角，以保持水分子的结构。采用晶格常数为3.615的面心立方单元对具有1 nm 厚度的铜板进行建模，得到由六层铜原子组成的铜板。铜原子的相对位置在之后的模拟中不进行更新，这相当于忽略铜原子的热运动。这一假设在冰黏附的分子模拟中被广泛采用[27-29]，在研究水在固体表面上的接触角时也有采用[34-35]。由于本文并不对铜原子的相对位置进行更新，所以铜原子相互作用势的选择并不是唯一的，甚至可以说是任意的。为满足所有种类的原子之间都具有对相互作用类型的要求，铜原子的相互作用采用嵌入原子模型（eam）。水分子与水分子之间和水分子与铜壁面之间的相互作用采用Lennard-Jones12-6 势函数和库仑相互作用来描述，设置L-J 势的截断半径为10 Å（1Å=1×10-10m），库仑相互作用的截断距离为8.5 Å，超过这一距离的库仑相互作用采用PPPM/TIP4P 在倒数空间中计算。

表1 水分子模型参数（TIP4P/ICE）Table 1 Model parameters of water molecule（TIP4P/ICE）

式中，E为两粒子之间的势能；ε为势阱深度，描述了两个粒子之间的相互作用强度；σ为两个分子处于平衡位置时的距离；C是能量转换常数；qi和qj是i原子和j原子上的电荷；r是两个分子之间的距离；rc为对应的截断距离。

水在紫铜表面的静态接触角θ为86.4°[36]，根据静态接触角与势阱深度的线性关系θ=178.57°-497.41°×εO-Cu[35]，本文选用εO-Cu=0.1853。Cu和O之间的平衡距离参数根据Lorentz-Berthelot 混合规则[37]确定。

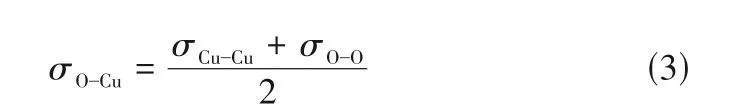
铜原子之间平衡距离σCu-Cu=2.3377 Å[38]，得到σO-Cu=2.7523 Å。考虑到重力在纳米尺度上远不如相互作用势重要，因此本文忽略了重力的影响。模拟体系中的相互作用参数列于表2，其单位选用LAMMPS中的 real 单位制。

表2 各组分之间的相互作用参数Table 2 Interaction parameters between components

1.1.2 物理模型 冰块由六角形冰晶胞在x、y、z三个方向上复制得到，包含2160 个水分子，如图1（a）所示。扩大模拟盒子并沿冰晶体基面{0001}[39]引入铜板，如图1（b）所示。融化界面区域的冰块，形成1.5 nm 厚的液层，以保证在不同工况下进行结冰模拟时形成对应的准液体层，如图1（c）所示。为保证荷电工况下体系呈现出电中性，在冰块上方引入一块可以上下活动的铜板，该铜板带有与下铜板等量相反的电荷，如图1（d）所示。整个模拟空间尺寸为4.13 nm×3.88 nm×11.50 nm，x和y方向采用周期性边界。由于本文中z方向的周期性并没有意义且为了节省计算资源，将z方向设为固定边界条件。同时将模拟盒子z方向的周期性图像变为空(体积因子设置为 3)[40]，以满足长程库仑力求解器要求的周期性边界条件。

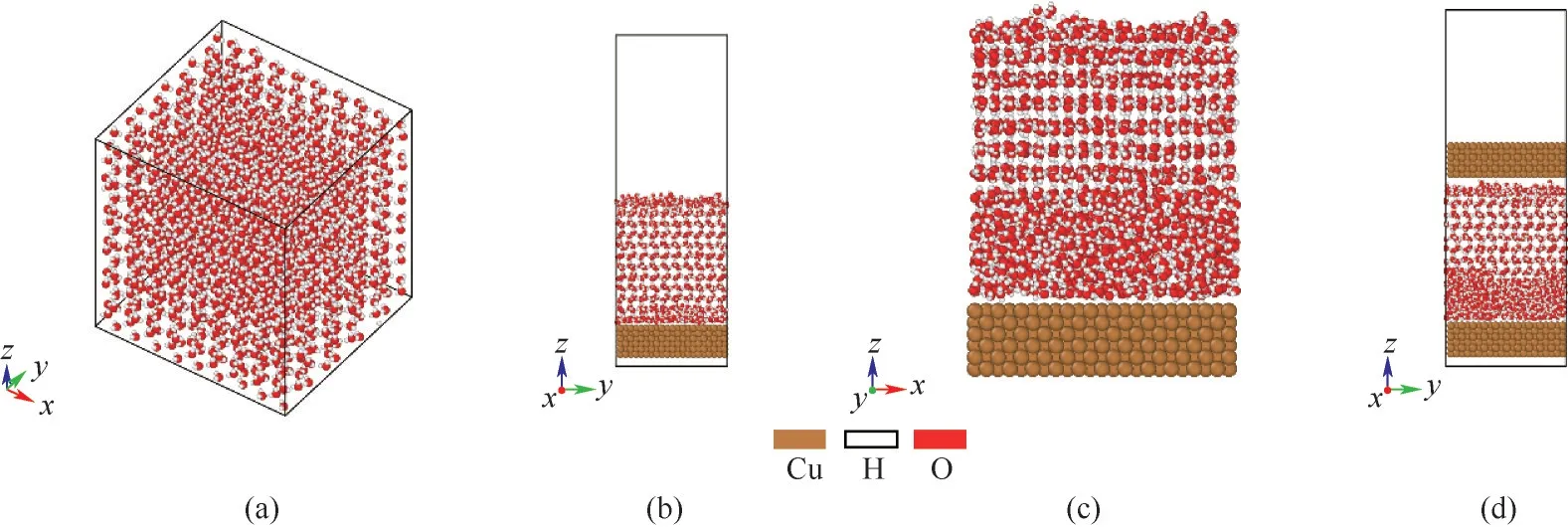
图1 物理模型建模过程Fig.1 Modeling process of physical model

1.2 平衡模拟和冰水判定

本文中模拟分为平衡和脱附两个阶段。在平衡阶段，以上述准备好的物理模型为初始结构，保持温度T=255 K，铜板分别加载不同电荷量（Q=0 e/nm2、脉 冲 交 变Qperiod=±0.1123 e/nm2、静 电Qstatic=±0.1123 e/nm2）进行三个相互独立的结冰模拟。本文中壁面带电量与文献[40]中的数值在同一量级。当铜壁面荷电时，电荷平均地加载到与冰块直接接触的那一层铜原子上[40-41]，如图2所示。铜板静态荷电和脉冲荷电时，下铜板带电荷铜原子（数量N=242）的带电量随时间变化如图3（a）、（b）所示，上铜板带电荷铜原子时刻保持带等量的相反电荷。模拟过程中，冰块采用Nose-Hoover 方法来控制温度恒定在指定温度，模拟时间步长为1 fs，耦合时间常数为

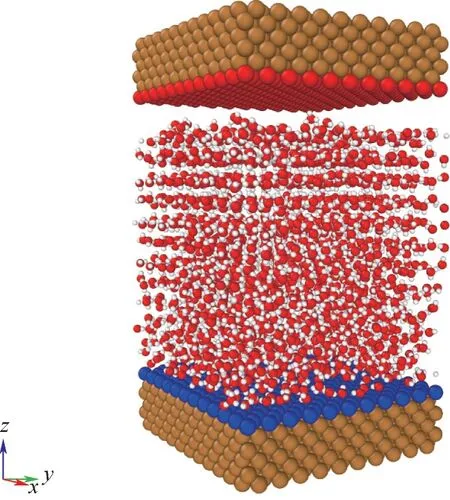
图2 铜板荷电时的模型图（红色铜原子带正电荷，蓝色铜原子带负电荷）Fig.2 Model diagram of charged copper plate (copper atoms in red are positively charged, and copper atoms in blue are negatively charged)

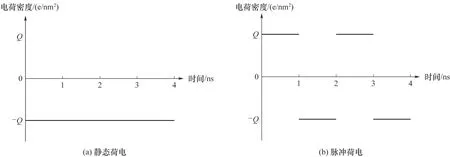
图3 下铜板原子的荷电量时变关系Fig.3 The time-varying relationship of the charge of the lower copper plate atoms

0.1 ps，每1 ps进行一次数据采集。

采用键序参数Ql来区分水分子是处于“固态”还是“液态”[42-43]。根据文献[44-45]的方法，计算了温度T=255 K 下六角形冰和液态水的键序参数Q6，其概率密度函数(probability density function，PDF)如图4所示。同温度下冰和水的Q6曲线的交点作为区分水分子状态的分界线，高于该值水分子处于“固态”，否则处于“液态”。可以得到在255 K 时的代表分界线的Q6值为0.3992。如果冰分子的数目随时间没有明显的上升，则可判定冰块和壁面体系已经达到平衡，界面区域的准液体层形成，冰块稳定地附着在铜板上，可以进行准液体层的分析以及脱附过程的模拟。

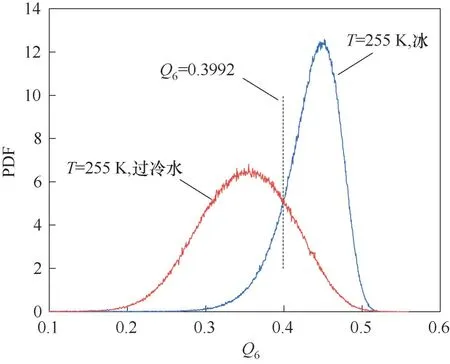
图4 冰和过冷水Q6的概率密度函数图Fig.4 Probability density function of Q6 of ice and water

1.3 脱附模拟和黏附强度的测量

在脱附阶段，为保证体系电荷守恒而引入的上铜板可以上下活动，下铜板固定，给所有水分子施加一个沿铜板法线方向的拉力，使其具有远离下铜板的趋势，如图5 所示。通常，拉力的大小从零开始，随时间步长线性增加，使基底和冰块之间相互作用的z方向分量表现为吸引力，直到拉力足够大，使冰块脱离壁面[29,46]。记录过程中吸引力大小与相应拉力的值，再利用冰-基体接触面积进行换算，将吸引力和拉力的值转化为界面法向应力和外加法向应力。

图5 外加拉力使冰块脱附示意图Fig.5 Schematic diagram of applying tension to make ice block desorb

式中，F是基底对冰块的吸附力或拉力附加给冰块的拉力；A是冰-基底接触面积。

本文采用给所有水分子施加恒定拉力的方法进行黏附强度测量。在每种工况下选择10 个不同时刻的构型，测定每个构型中冰块在2.5 ns 内脱附的最小拉力，再将10个构型中的最小脱离应力作为该工况下的黏附强度。

2 结果与分析

本文讨论了温度T=255 K 时的铜板脉冲荷电以及静电荷电的工况，同时以壁面不带电荷时冰和过冷水的黏附强度为参照，表征了黏附强度降低的幅度。过冷水由冰块升温至350 K 融化后，再降温到目标温度得到。

2.1 冰块生长和准液体层形成

图6（a）显示了平衡阶段被判定为冰的水分子数目变化。相对于冰块生长的平衡，大块水的平衡要快的多，因而平衡时间较短。在温度T=255 K 且壁面不带电荷（Q=0 e/nm2）时，组成冰块的水分子数目在上升到一定程度后，会在一定的范围内波动，这归因于分子的热运动。在温度T=255 K 且铜板带脉冲电荷Qperiod=±0.1123 e/nm2时，尤其是平衡时间t=30.0～40.0 ns这一区间，冰分子数目的变化呈现出明显的锯齿状，即在铜板电荷产生的电场方向转变时，会在一定程度上打乱规则的六角形冰结构，而在随后的时间里冰块继续生长，直到下一次电场方向转变的时刻再次被破坏。温度T=255 K 且壁面带静电Qstatic=±0.1123 e/nm2时，并没有出现冰分子数目呈现锯齿状的现象。可以推断，在冰分子数目不再明显增长时，体系已经处于平衡状态。图6（b）展示了一系列不同时刻的模型快照，并在图6（a）中的相应位置用圆圈数字进行了标记。对应冰分子数量的增长，从模型快照中很容易观察到冰块的生长，同时也可以观察到冰块主体部分规则的冰双层结构以及界面区域的准液体层。准液体层的分析放在后面进行，首先研究不同工况下的黏附强度。

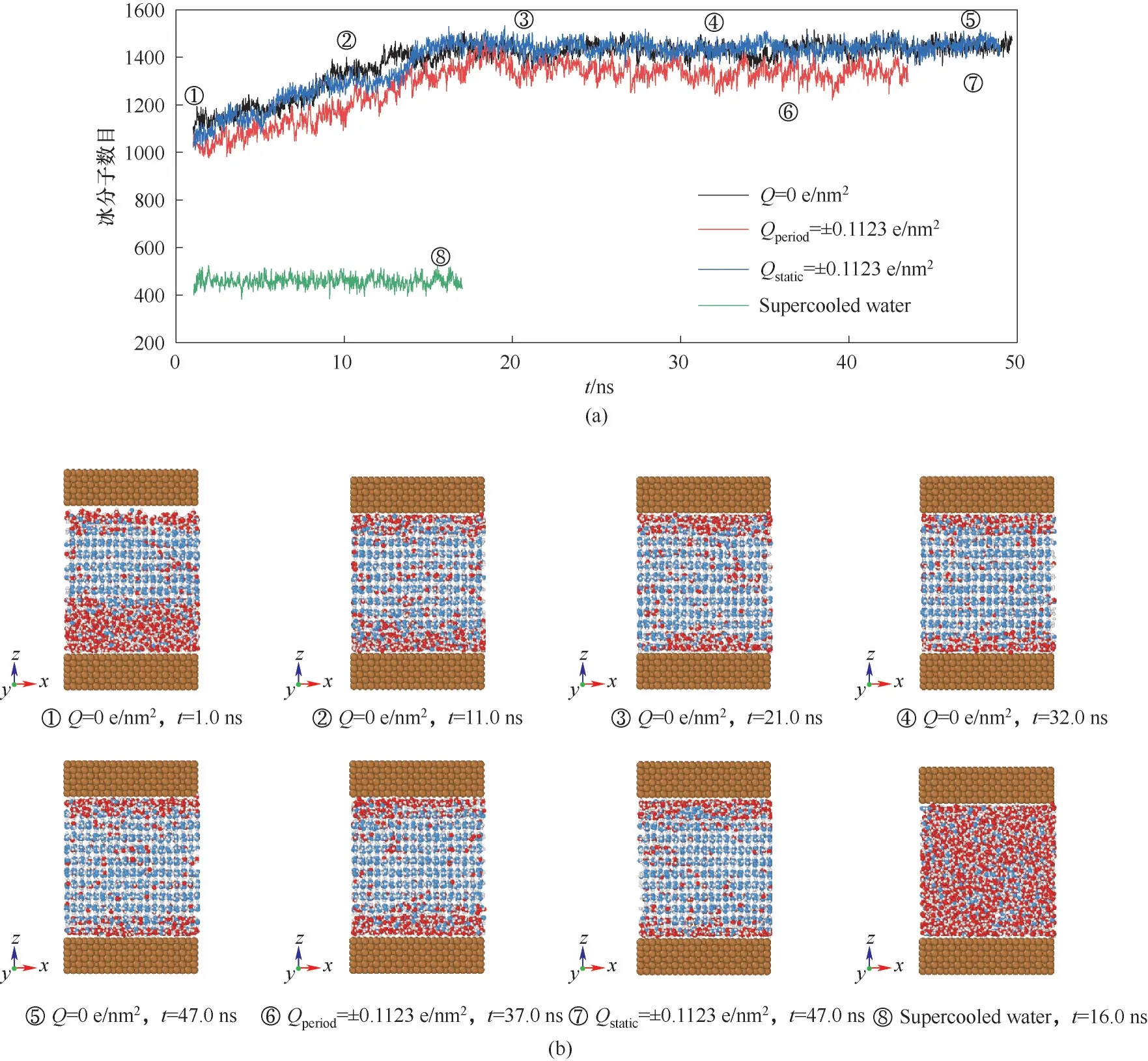
图6 类冰水分子数目随时间的变化及对应时刻的模型快照（黄铜色为铜原子，红色为类液水分子，蓝色为类冰水分子，白色为氢原子）Fig.6 Time-dependent changes in the number of ice-like water molecules and model snapshots at corresponding moments (brass are copper atoms, red are “liquid” water molecules, blue are “solid” water molecules, and white are hydrogen atoms)

2.2 冰的黏附强度

在大块的水中结冰需要漫长的形核过程[47]，这提供了充分的时间来测量过冷水的黏附强度。因此，本文对4 种工况均进行了10 次初始构型不同（体系平衡后取连续的10.0 ns，每隔1.0 ns 选取一个构型）的相互独立的脱附模拟。

以T=255 K，Qperiod=±0.1123 e/nm2时为例，取t=33.5 ns 的构型为初始构型。脱离应力的测量需要不断更改给定的拉力大小，根据冰块在上一测试拉力下是否脱附对拉力进行调整，每次调整的拉力大小间隔约使外加法向应力增加或减少1.0 MPa。图7记录了在测定该构型脱离应力过程中，其中6种不同拉力下冰块的质心（center of mass，COM）纵坐标随时间的变化。下铜板的荷电情况也标在图7 中。可以观察到，脱附模拟过程中电荷产生的电场方向发生了两次变化。冰块质心坐标的迅速升高标志着冰块从铜板上剥离。在外加法向应力σpull=135.4和140.3 MPa 时，冰块质心保持在同一水平，没有发生脱附的现象。将外加法向应力增加到141.2 MPa时，冰块在拉力作用2.4 ns 后发生脱附。然而将外加法向应力增加到143.1 MPa 时，冰块却意外地没有脱附。当进一步将外加法向应力增加到144.1 MPa 和147.0 MPa 时，冰块脱附的时间点有所提前，且在较大外力作用时具有更大的提前幅度，这是因为外加法向应力增大，脱附概率增加，可以在更短的时间内实现脱附。综上，在T=255 K、Qperiod=±0.1123 e/nm2的工况下，t=33.5 ns 时刻的脱离应力为141.2 MPa。

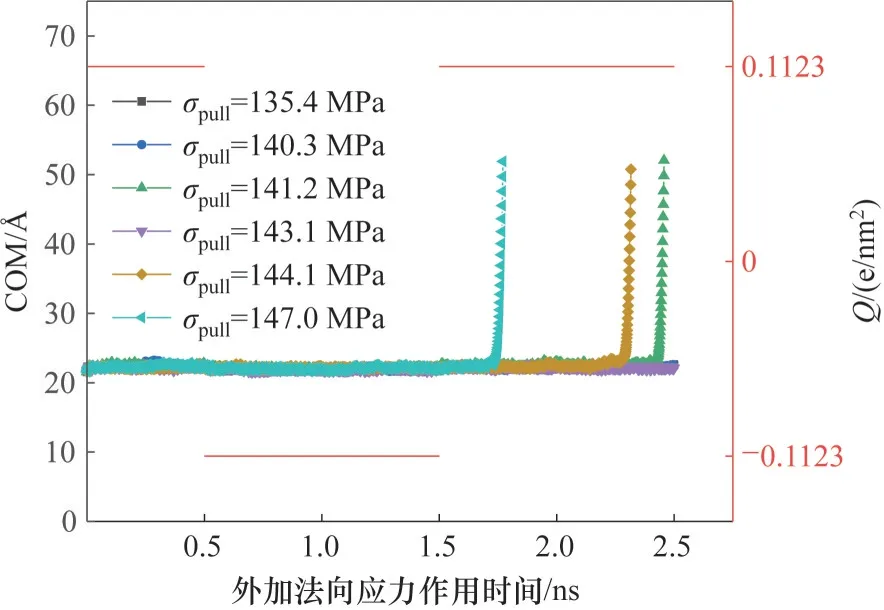
图7 T=255 K，Qperiod=±0.1123 e/nm2，t=33.5 ns时，不同外加法向应力下的脱附模拟中冰块质心的位置变化Fig.7 The position change of the ice mass center in the stripping simulation under different applied normal stress when T=255 K, Qperiod=±0.1123 e/nm2,t=33.5 ns

该 工 况 下（T=255 K，Qperiod=±0.1123 e/nm2）t=33.5～42.5 ns 时间段内的10 个构型（每1.0 ns 选取一个构型）的脱离应力测定结果如图8 所示。在样本范围内，t=35.5 ns时的脱离应力最小，为130.6 MPa。综上，T=255 K、Qperiod=±0.1123 e/nm2的工况下，冰的黏附强度为130.6 MPa。

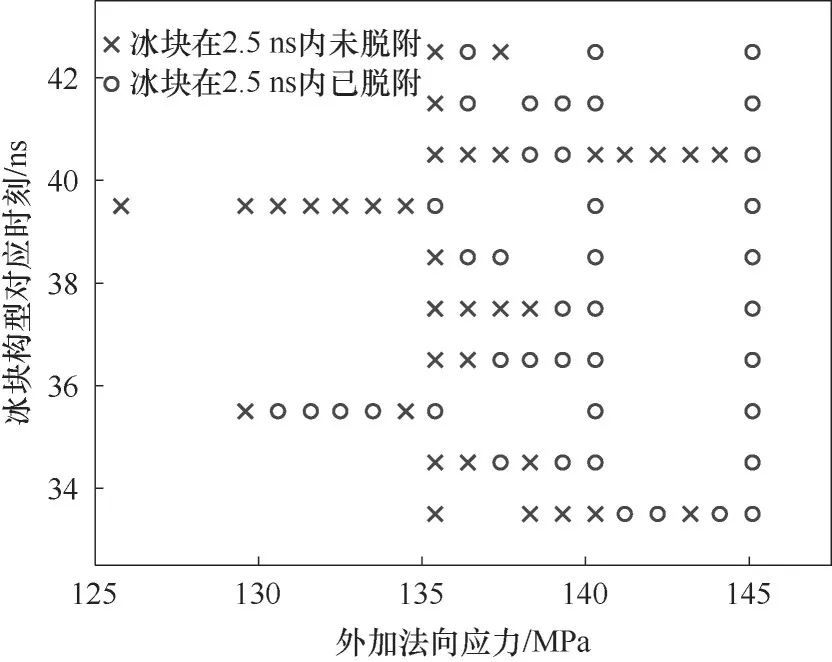
图8 T=255 K，Qperiod=±0.1123 e/nm2，t=33.5～42.5 ns时，各个冰块构型在不同外加法向应力下的脱附情况Fig.8 Stripping of ice under different applied normal stresses when T=255 K，Qperiod=±0.1123 e/nm2，t=33.5～42.5 ns

图9(a)记录了各种工况下10次独立脱附模拟得到的脱离应力。以这10 个脱离应力最小值作为这种工况下的黏附强度，如图9(b)所示。

图9(b)显示，在255 K 时，Q=0 e/nm2的工况下的冰块和铜板之间的黏附强度145.1 MPa 与过冷水与铜板之间的黏附强度99.6 MPa 之差决定了黏附强度可以减小的最大限度约为45.5 MPa。以Q=0 e/m2工况下，黏附强度可减少的最大限度为参照，Qperiod=±0.1123 e/nm2和Qstatic=±0.1123 e/nm2时的黏附强度分别为130.6 和148.0 MPa，降低的幅度分别为31.9%和-6.4%。这表明电荷的存在会增强壁面和水之间的库仑相互作用，从而增加冰的黏附强度，然而交变电场的存在却使冰块的黏附强度降低。造成这一现象的原因是脱附模拟冰块初始结构的差异，即平衡阶段对应时刻的冰块的准液体层厚度差异。

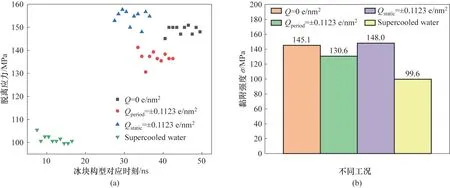
图9 不同工况下的脱离应力以及黏附强度Fig.9 Detaching stress and adhesion strength under different conditions

图10展现了平衡阶段平衡后的冰块静态结构。沿铜表面法线方向上以2 Å 的厚度进行分层，将同一层内水分子的键序参数Q6求取平均值，得到Q6(Z)，以判断该层水分子处于固态还是液态，其中键序参数Q6每1 ps 采集一次，采集的范围是与脱附模拟取样时间段对应的10.0 ns。图中虚线与实线交点的横坐标即为冰水界面的坐标，尽管实际上的冰水界面有一个过渡的区域。Q6(Z)的分布再次表明，在铜表面一定高度范围内水分子的晶体状结构遭到破坏，存在水分子无序排列的准液体层。由于各种工况下铜板最上层原子的坐标（Z=-1.8075 Å）相同，因此冰水界面的坐标直接反映了该工况下的准液体层厚度。这与期望的一样，准液体层的厚度正是随着冰块黏附强度的降低而增厚，因此壁面加载脉冲电荷是增加准液体层厚度的有效方式，从而成为一种减小冰黏附强度的有效手段。

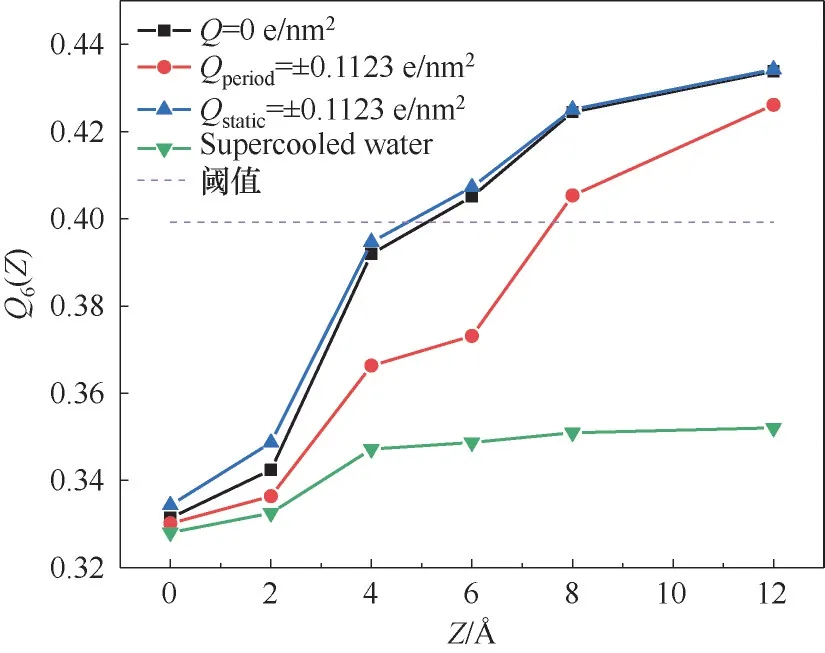
图10 体系平衡时的冰块静态结构（虚线为区分冰和水的阈值，虚线之上为冰，虚线之下为水）Fig.10 The static structure of the ice cube when the system is in equilibrium (the dotted line is the threshold for distinguishing ice and water； above the dotted line is ice, and below the dotted line is water)

3 结 论

本文使用全原子模型的分子动力学模拟研究了光滑铜表面上黏附冰的脱附行为，采用序参量进行水分子的冰水判定，以冰块质心位置和脱离应力大小对冰块的脱附过程进行了定量表征，量化了255 K 时不同壁面条件下冰块的黏附强度，得到如下结论。

在壁面施加静态电荷无法降低冰的黏附强度，但壁面施加脉冲电荷可降低冰在壁面的黏附强度。壁面静态荷电Qstatic=±0.1123 e/nm2对准液体层厚度影响不大，由于壁面电荷的存在增大了壁面与水分子之间的库伦相互作用，导致冰的黏附强度由壁面不带电荷时的145.1 MPa增大到148.0 MPa。壁面脉冲荷电Qperiod=±0.1123 e/nm2会使冰块与固体壁面之间的准液体层加厚，从而使冰的黏附强度降低到130.6 MPa。以过冷水与铜板之间的黏附强度99.6 MPa 为参照，降低幅度达到31.9%。本文从原子尺度上揭示了准液体层在冰脱附过程中起到的关键作用，证明了壁面脉冲荷电是一种有效促进壁面上黏附冰脱附的方法。

符 号 说 明

A——冰-基底接触面积，nm2

C——能量转换常数

E——两粒子之间的势能，kcal/mol

F——基底对冰块的吸附力或外加给冰块的拉力，N

lOM——四点TIP4P/ICE 水模型中无质量的电荷点与O原子的距离，Å

MO,MH——分别为氧原子和氢原子的分子量，g/mol

Ql——键序参数

Qperiod,Qstatic——分别为脉冲荷电的电荷密度和静态荷电的电荷密度，e/nm2

qPt,qC——分别为单个Pt 原子和单个C 原子的荷电量，e

qO,qH——分别为氧原子和氢原子上的电荷，e

qi,qj——i原子和j原子上的电荷，e

r——两个分子之间的距离，Å

rc——对应的截断距离，Å

r0——四点TIP4P/ICE水模型中O—H键键长，Å

T——热力学温度，K

t——平衡时间，ns

ε——势阱深度，kcal/mol

θ0——四点TIP4P/ICE 水模型中H—O—H 键角，（°）

σ——两个分子处于平衡位置时的距离，Å

下角标

period——脉冲荷电

static——静态荷电