智能电网中用电感知的数据分析需求响应方案研究
李鑫,杨方,肖湘晨,王海元,黄红桥
(1. 国网湖南省电力有限公司供电服务中心(计量中心),长沙 410004;2. 智能电气量测与应用技术湖南省重点实验室,长沙 410004)
0 引 言
住宅、商业、工业和交通等不同类型的用电需求的快速增长,加大了电网的负担[1]。其中住宅用电约占总电力消耗的38%,且预计将保持0.3%的年增长率。为满足这一增长需求,电力企业需要建立新的基础设施,或者采取手段削减高峰负荷需求,使当前资源能够满足用户负荷需求。为减少负荷需求,电力企业需要对连接负荷的需求响应进行管理,以降低电网总体负担[2-3]。
目前,研究人员提出了一些对住宅用电的DR管理策略。如文献[4]提出了用于智能建筑的DR管理方案,基于多代理少数者博弈以降低电网的高峰用电需求。但该方案不适用于未部署太阳能PV板的家庭。另外,智能化数据分析方法也用于进行需求响应管理,如文献[5-6]分析从SHs采集的数据,并利用决策树和支持向量机进行窃电检测。但该方案着眼于SH中的数据分析,且并未通过SHs的DR管理来降低高峰负荷。文献[7]利用最小二乘支持向量回归识别用电过量的SHs,并有针对性地进行DR管理。但该方案未考虑用户负荷需求的瞬时变化,且DR管理方案仅针对用电量异常的SHs。文献[8]利用不同家庭的采集数据对住宅电器进行DR管理,降低电网峰值负荷。根据从用户调查中计算出的各种指标来促发DR控制事件。但其假定每个家庭的负荷曲线是相同的,且对每个家庭中不同电器使用了相同的使用模式。
为此,提出了SHs的用电感知数据分析需求响应(DADR)管理方案,通过数据分析降低电网高峰负荷。其主要工作和创新如下:(1)通过分析SHs的用电数据,设计了各种不同因子,例如电器调节系数,电器优先级指标,电器削负荷优先级等;(2)分别提出用于用户和电力企业的不同算法,由此制定SHs中的DR决策,降低SG的高峰负荷。此外,对SHs中的瞬时负荷变化进行实时管理,以保持电网的负荷曲线。
1 本文方案概述
本章将详细介绍智能家居(SHs)的DR管理方案,从而在每个时隙开始时,实时降低智能电网(SG)在高峰时段的负荷。文中方法使用了固定的计费策略,以确保不会在电网中产生回升高峰[9-10]。为了将提出的方案应用于现实中,需要将SHs的用电数据传递至电力企业。图1给出了SHs和电力企业服务器之间的通信场景。通过实施轻量级加密安全机制来确保数据的安全性和隐私性,该安全机制不会影响到整体系统性能。如图1所示,数据采集过程被分为三层。第1层中,SHs中的设备将其用电数据传递至各自家庭中的本地控制器。第2层利用接入点(APs),将本地控制器的采集数据传递至第3层中的SG服务器。在数据传递至SG服务器后,立即执行数据分析以做出DR决策,其后将DR决策转回本地家庭控制器,以控制各自家庭中的设备。
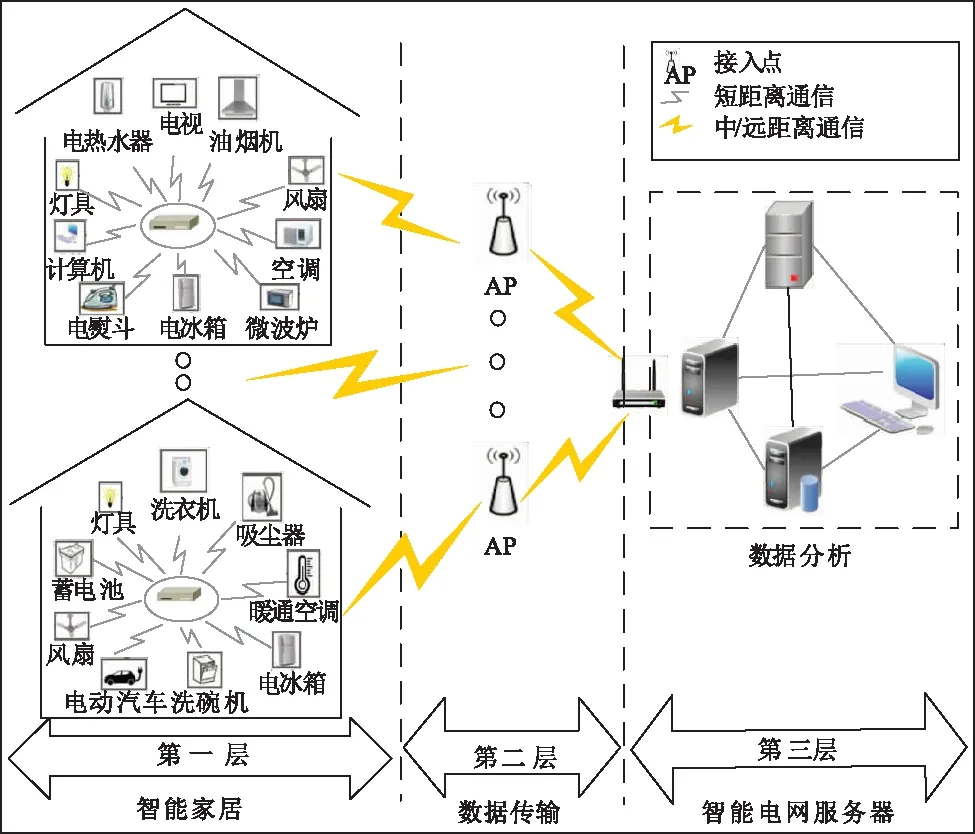
图1 SHs与SG的通信简图Fig.1 Communication diagram of SHs and SG
将完整的一天划分为多个等间隔时隙,并在每个时隙内进行高峰负荷管理。设电网在第t个时隙开始时的发电容量为G(t)(单位kW)(考虑到装机容量以及可再生能源发电),SHs的总数量为n,第i个家庭在第t个时隙的用电需求为Hu(i,t)(单位kW)。若存在以下情况,则应该对电网负荷进行管理:
(1)
在这种情况下需要削减负荷需求,则总能量缺口为:
(2)
式中 Δt表示第t个时隙的持续时长。
为填补式(2)中的缺口,基于从SHs采集到的数据在SHs中进行负荷需求削减。为此,提出的方案使用ZigBEE、WiFi和IEEE 802.15.4a/c/f技术,将各种电器的数据传递至本地控制器;并使用WiFi、WiMAX和长期演进(LTE)技术将数据从本地控制器传递至电力企业服务器[11]。图2给出了完整方案流程图。

图2 提出的方案的流程图Fig.2 Flow chart of the proposed scheme
2 方案的重要环节
2.1 DR决策制定中使用的因子
本小节将解释直接影响DR决策过程的各种因子的计算方式。这些因子主要取决于SHs采集数据,可通过分析每个时隙的数据来计算。
(1)电器利用系数(AUF):AUF为某个电器的功率与家庭总耗电量的比率,表示为:
(3)
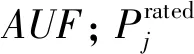
(2)电器运行时长系数(ARF):ARF表示特定电器在上一个时隙过程中处于运行状态(打开)的时长占比。举例来说,设每时隙为15分钟,电器“A”在一个时隙中开启了12分钟,则“A”的ARF为0.8。利用上一个时隙采集到的运行状态相关数据,计算出第i个SH中第j个电器的ARF:
(4)
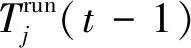
(3)电器调节系数(AAF):AAF表示是否可通过提出的方案对该电器进行调节(即负荷削减)。AAF数值为0或1,取决于以下条件(本文方案仅在AAF=1的情况下进行电器调节):
(5)
式中AAFj(i,t)为第i个SH的第j个设备的调节系数;τ为预定义阈值;Sj(i)表示第j个设备的当前状态,计算如下:
(6)
在计算AAF数值式还使用了两个列表,D和E。列表中保存了不同类型电器的相关信息。列表E包含不受DADR方案控制的所有应急设备,例如:灯具、风扇和医疗设备等,因此此类电器的AAF均设为0。列表D包含洗衣机、电熨斗等各种电器和所有厨房电器(例如微波炉、电饭锅和烤箱等)。
AAF的意义在于,设备在完成某部分的周期工作时间(由τ指定)的情况下不应该进行调节,否则将会影响到正在进行的工作。此外,AAF确保了应急电器不受DR管理的影响。
(4)电器优先级指标(API):API是最重要的参数,通过分析从各种SHs所采集到的数据而计算[12-21]。API用于衡量某个电器相较于其他电器,在负荷削减中的优先级。在优先级计算中,还考虑到用户舒适度(即该电器在负荷条件相似的其他家庭中的使用情况)。这是因为,负荷条件相似的家庭会对DR表现出相似的用电模式响应。因此,可将其作为计算SH中电器优先级的指标,而不用考虑所有SHs。通过用户档案找到负荷条件相似的家庭并进行聚类。为此,提出的方案中使用了k均值聚类技术。k均值聚类中涉及到以下步骤:
步骤1:将每个用户随机分配至任意一个用户群集c(c= 1, 2,…,C)。
步骤2:计算每个群集的中心:
(7)
式中μc为第c个群集的中心;xi为第i个用户的特征值;Cc为群集c中的用户集合;Nc为Cc中的用户数量。
步骤3:将每个用户分配到群集中,以使其特征值与新中心(d(x,μ))之间的距离为最小值:
(8)
式中x和μ分别表示所有用户和群集中心的特征向量;S为特征向量大小。
步骤4:重复步骤2和步骤3,直至群集中心不再发生显著变化(即群集保持稳定)。
基于Hu,使用上述步骤为每个时隙生成SHs群集,以考虑电器使用的动态特性。一旦群集稳定,则计算出电器j的API(APIj(i,t)):
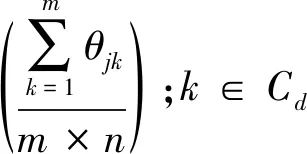
(9)
式中n为连接到SG的SHs总数量;m为群集Cd中的SHs数量;Cd表示在第i个SH的Hu方面表现出相同行为的用户群集(使用式(7)计算);θ为比例常数。θjk值表示第k个SH中电器j的当前工作状态,通过以下公式计算:
(10)
即第k个SH中,j为开启状态时θjk=1,否则θjk=0。式(8)中的分子表示群集Cd中,第j个电器为开启状态的SHs的总数量。m表示群集Cd中SHs总数量,n表示SHs总数量,由此计算出第i个SH中电器j的优先级。该计算的基础在于,相似SHs中某电器的使用频率越高,则其优先级也应该越高。由此,电器的API数值越大,则该电器在其SH中的优先级越高。
(5)电器削负荷优先级(ACP):使用ACP因子,增加SH中(在被电力企业关闭后)频繁被用户重新打开的电器的优先级。因此,ACP数值越高,表示该电器的优先级越高,不应被削减负荷。该因子计算如下:
(11)
式中ACPj(i,t)为第i个SH中第j个电器在第t个时隙的ACP值;γ为比例常数;pnj表示一天中第i个SH中的电器j被电力企业所关闭的次数。利用式(8)计算出APIj(i,t)的数值,从列表AP(使用算法1建立)中提取出pnj的数值。列表AP中包含被电力企业进行过负荷削减的所有SHs的所遇电器的pn值。
(6)相对耗电指数(RCI):RCI有助于识别耗电量较大的家庭。第t个时隙中,第i个SH的RCI值计算为:
(12)
上述公式将计算第i个SH相对于其所在群集Cd中耗电量最大的SH的相对能耗。RCI数值越高,表明第i个SH相较于其他RCI值较低的SHs的耗电量越大。
(7)用户削负荷系数(CCF):CCF是提出的DADR方法中,唯一需要用户指定的因子。CCF表示电力企业在任何时间可削减负荷的最大期望限值。若将CCF值设为1%,则削减负荷不会超过总负荷的1%。用户可增加或减少其CCF值,以控制其在DR管理过程中的参与度。
CCF还被用于计算用户满意度和舒适度,因为用户将根据自身适用情况来设定CCF。若负荷削减低于或等于用户指定的CCF值,则考虑用户是满意的。基于CCF,可通过负荷削减来节约第t个时隙中的能耗(Es(i,t)):
(13)
式中CCF(i,t)为第t个时隙的第i个SH中用户指定CCF值。式(13)中,EC(i)表示通过实际负荷削减(通过式(14)确定),第i个SH累积节约的电量。Es(i,t)的下界设为0,以避免任何负值。
(14)
式中Ej表示在Δt持续时间内第j个电器的削减电量,计算为:
(15)
如式(14)所示,在一天开始时Ec(i)的值被设为0。其他时间,将关闭电器(j)所节约的电量加入到Ec(i)中。
2.2 制定DR决策
使用前文定义的因子,通过提出的两个算法来制定DR决策。第一个算法(以用户为中心的DADR算法)从用户的角度出发,通过考虑用户舒适度来降低高峰负荷。该算法中,负荷削减取决于用户指定的CCF值,且不会超过该数值。因此,该算法所降低的高峰负荷有限,但能够确保负荷削减不会影响到用户舒适度。第二个算法(以电企为中心的DADR算法)从电网角度出发,确保削减更多的高峰负荷,但可能会降低用户舒适度。为对此进行补偿,需要给予用户额外的奖励。电力企业可根据情况仅使用算法1,或同时使用算法1和算法2。使用提出的算法,通过削减SH的负荷需求来保持SG的负荷曲线平稳。
首先,使用算法1降低SHs中的负荷。该算法的第一步是计算所有SHs中所有电器的API和ACP。其后,根据电器的ACP值,按升序存储在列表中。列表的意义在于,电器在该列表中排名最前,该电器在其他SHs中使用最少,因此优先级也最低。对于该电器(k),计算AAF值,并对AAF≠0的电器进行负荷削减:计算出相应SH的Es(i,t)值(基于CCF),若Ek 算法1: 以用户为中心CC-DADR算法 1.for (i= 1;i≤s;i++) do//s为SHs的总数量 2.∀j,计算API //j为SH中的电器 3.∀j,计算API 4.end for 5.按升序对ACPj(i,t) 进行排序并保存在列表中 7.for (k= 1;k≤n;k++) do//n为中的总电器数量 8.提取相关家庭(h) 9.使用式(4)计算第k个设备的AAF 10.if (AAFk(h,t)≠0) then 11.得到家庭h的CCF 12.使用式(12)计算Es(h,t) 13.if (Ek 14.关闭电器k 15.在列表AP中保存电器k;pnk=pnk+1 16.将该决策传递至h的本地控制器 17.使用式(14)更新Ec(i) 19.end if 20.end if 21.end for 22.end while 由此,算法1根据用户指定的CCF值,减少了家庭中的负荷。然而,在遵守每个SH的CCF的情况下,电网负荷可能依然超过其发电容量。这种情况下,需要使用算法2以使电网负荷曲线保持平稳。 算法2 :以企业为中心 UC-DADR算法 1.for (i= 1;i≤s;i++) do//s为SHs的总数量 2.使用式(11)计算RCI 3.for (k= 1;k≤m;k++) do //m为1个SH中的总电器数 4.使用式(3)计算AUF 5.计算Appk(i,t)=RCI(i,t)×AUFk(i,t) 6.将Appk(i,t),k和i的数值保存在列表中。 7.end for 8.end for 9.根据Appk(i,t)数值,以降序对列表进行排序 10.for (q= 1;q≤n;q++) do //n为列表中的总电器数 13.关闭电器q 14.将该决策传递至h的本地控制器 16.使用式(15)更新Ec(i) 17.end while 18.end for 瞬时负荷变化管理:由于负荷具有本质上的动态性,且用户可在任何时候解除SH中的负荷控制,因此在任何DR管理方案中,对负荷需求的瞬时变化进行管理是至关重要的。为此,提出的方案采用了算法3。 算法3: 1.当1个新设备d(能量要求Ed)SHs中瞬时负荷变化的管理被打开时 3.打开d 4.若d在列表AP中,则将其从表中移除 5.else if(Sig=‘urgent’) then//Sig为优先级信号 6.for (∀/j, 其中Sj(i)=1) do//j表示电器,i表示SH 7.得到APIj(i,t) ,并将其在列表Temp中按升序排序 8. end for 9.∀/j∈Temp 10.从Temp中关闭电器,直至∑Ej≥Ed 11.将这些电器保存在列表AP中;pnj= 1 12.打开新设备d 13.else 14.将d保存在列表AP中;pnd=pnd+ 1 15.end if 16.当一个当前设备o(能耗Eo)被关闭时 17.if (Sig≠ ‘urgen’) then 19.else 20.break; 21.end if 文中在仿真环境中,测试了所提方案在降低电网高峰负荷需求方面的有效性。实验设置如下,每时隙持续时长为15 min。选用文献[22]的SHs数据集,提供了家庭中各种用途的每小时能耗值,包括照明、供暖、降温、热水器、基础设施及各种杂项。将这些数值调整为15 min间隔,并根据EIA提供的用电模式[23]分配至相应电器。表1给出了实验中使用的其他参数。仿真中,为每户家庭随机指定CCF值。 表1 仿真参数的设置Tab.1 Setting of simulation parameters 提出的DADR方案的主要目的是降低高峰负荷。在方案评价中,选取了真实电力场景进行案例分析。电网发电数据[24]和负荷数据的数值单位为kW·h,将发电数据按比例缩小125倍;负荷区域的用电量缩小2.25倍。考虑负荷区域包含200个SHs。图3给出了发电数据和用电数据的最终数值。从中可以观察到,高峰负荷需求出现在午间时段(12点~16点),其后负荷需求开始下降。将负荷需求曲线建模为始终与现实世界的负荷需求相一致。 图3 电网的负荷需求曲线Fig.3 Load demand curve of power grid 在用电需求超过发电容量的时隙中应用提出的方案。首先对SHs进行聚类,以计算所有SHs的每个电器的API值。为此,对于每个时隙,将Hu方面表现出相似特征的家庭聚类在一起,根据案例分析中SHs的数量,将群集数量设为4(即C=4)。基于群集信息,分别使用式(8)和式(10)计算出所有电器的API和ACP值。 为削减高峰负荷需求,电力企业首先采用CC-DADR算法;若未成功削减高峰负荷,则电企再利用UC-DADR算法。图3给出了单独应用CC-DADR算法,以及先后应用两种算法后的电网负荷需求情况。图3还给出了仅使用UC-DADR算法进行DR管理的样例。从中可观察到,仅使用UC-DADR算法,与使用两种算法,实现了较为相似的负荷削减。但仅使用UC-DADR算法,会对用户舒适度造成较大影响。另外,单独应用CC-DADR算法,不能在所有时隙中成功削减高峰负荷。举例来说,在14点时原始负荷需求为1 432 kW,在应用CC-DADR算法后降至1 324.5 kW,负荷需求依然大于发电容量。这种情况下,电企应采用UC-DADR算法,以使电网负荷曲线更加平稳。应用两种算法后,负荷需求在14点时降至1 264 kW(见图3)。由此证明,提出的方案使用CC-DADR和UC-DADR算法,能够有效降低电网高峰负荷,使其满足发电容量限制。 电网的高峰负荷削减也降低了SHs中的总能耗,由此减少了用户的电费支出: (16) 由表2可知,仅使用CC-DADR算法的电费支出高于其他案例。这是因为在CC-DADR算法中,SH中的负荷削减无法超过用户指定的CCF值。但某些情况下(SH5),仅使用CC-DADR算法,与仅使用UC-DADR算法或两种算法的电费支出相同。这是因为这种情况下,UC-DADR算法并未削减SH5的电器负荷。从表4还可发现,仅使用UC-DADR算法,与依次使用两种算法之间的电费支出差异并不大。 表2 使用DADR方案的电力成本(/元)Tab.2 Power cost of using DADR scheme (/yuan) 若用户可通过参与DADR方案降低电费支出,且舒适度未受过大影响,则考虑用户是满意的。提出的方案中使用两个度量,即电费节约和舒适度,来评价用户满意度。 (1)用户电费节约:用户参与文中方案,可从两方面节约支出。一方面,使用提出的方案在SHs中减少的能耗会直接降低电费支出,在每天结束时计算该数值。另一方面,用户会得到奖励,从而间接降低电费支出。在每月结束时计算出间接节约,可用于抵扣电费; (2)用户舒适度:提出的DADR方案通过两种方式确保用户舒适度。首先,通过观察相似负荷条件下的SHs中的电器使用趋势进行负荷削减。其次,提出的方案试图将一个SH中的负荷削减保持在CCF值之下(用户根据舒适度直接制定CCF值)。发现:使用CC-DADR算法时,负荷调整系数(LAF)值始终低于CCF值。但若电企使用了两种算法,少数情况下可能会发生LAF>CCF的情况。这种情况下,向用户发放更高的奖励,以补偿舒适度损失。在仅使用UC-DADR时,LAF常会超过平均CCF值。这表明UC-DADR算法忽视了用户设定的舒适度水平,因此不应该仅使用该算法削减高峰负荷。提出的方案以最优方式考虑了用户舒适性,尽量满足用户舒适和电企约束。 文中从电网总负荷削减和SHs成本节约方面,对提出的方案与当前其他方案进行了比较。图4展示了各方案的电网平均负荷降低和SH平均成本节约。从中可以观察到,使用提出的方案实现了最大的负荷降低,且成本节约与文献[8]大致相当;文献[7]的方案在两方面的表现最差。此外,提出的方案中还可以通过牺牲用户舒适度来进一步提高成本节约。可通过寻找用户和电企均可接收的舒适度与成本之间的最优权衡点来实现这一点。此外,如表3所示,与其他方案相比,提出的方案在更多数量的SHs上进行了测试,且SHs中包含的设备数量更多。从中可知,提出的方案在大规模实施中的可靠性更高。 图4 平均负荷削减和用户电费节约方面的比较Fig.4 Comparison between average load reduction and user electricity cost saving 表3 SHs数量和设备数量方面的比较Tab.3 Comparison of SHs quantity and equipment quantity 文章提出了数据分析需求响应(DADR)方案,以解决SG高峰负荷削减问题。基于从SHs中采集的数据,提出了各种因子的计算,以制定需求响应决策。提出的方案可视为2级控制方案,首先以不影响用户舒适度的方式进行负荷削减(仅使用CC-DADR算法)。若负荷需求依然超量,则使用第二级控制以进一步降低高峰负荷(使用UC-DADR算法)。这可能会降低用户舒适度,需要通过奖励方案对用户进行补偿。此外,提出的方案还能够处理SH的能耗模式中的瞬时负荷变化。结果表明提出的方案具有两方面优势:(1)有效管理SG中的高峰负荷需求;(2)降低用户电费支出。 未来,将探索在家庭数、电器数量和采样速率大幅提升的情况下的容错问题和大数据管理问题。此外,可加入更多SHs相关信息来测试提出的方案的效率。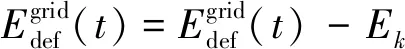

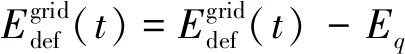


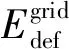
3 实验与结果

3.1 SG的负荷降低

3.2 SHs支出节约


3.3 用户满意度评价
3.4 与当前其他方案的比较


4 结束语

