路面识别技术在路噪主动控制降噪性能优化中的应用

徐格格，吕 晓，史晨路，朱玉刚，郑森

(1.河北工业大学 机械工程学院， 天津 300401；2.中汽研(天津)汽车工程研究有限公司， 天津 300300)

近年来，随着神经网络技术在路面识别领域的发展，越来越多学者将其成果运用到研究中。刘秋等[1]针对传统路面识别方法不能准确识别多种路面类型的问题，运用卷积神经网络识别路面，根据悬架系统在不同路面下的输出响应调节控制器参数，从而使可控悬架在不同路面下均能保持性能最优。王国微等[2]为使电动汽车具有较好的制动安全性，充分利用路面附着力，运用RBF神经网络识别路面，确定目标参数为识别出的最优滑移率，并设计出一种ABS控制策略将模糊控制和预测控制相结合。实例样车仿真结果表明提高了回收的制动能量。Zhu等[3]为解决瞬态路面下可控悬架的延迟问题，提出了一种结合监督式深度学习的预测控制方法，建立整车模型，采用有监督的深度学习(Y0LOv3)来识别瞬态道路，为半主动悬架实现提前预判，进而有效提高车辆乘坐舒适性。

鉴于此，将采用神经网络技术的路面识别方法与路噪主动控制相结合，通过安装在车身上的摄像头采集路面图像数据，运用卷积神经网络(CNN)识别3种不同路面类型。根据已建立的路噪模型进行仿真，找到3种路面对应的最优收敛因子。根据道路识别结果，调整不同道路下路噪主动控制系统的收敛因子，优化车辆降噪效果。

1 路噪主动控制

1.1 噪声主动控制原理

有源噪声控制(ANC)[4]的原理是声波的杨氏干涉原理。在规定区域内有意地增加1个次级声源，控制主要噪声信号。根据2种声波的抵消干扰条件，如果2种声信号的声波振幅相等，具有相反的相位，则2种声波会在空间中进行抵消，产成消声的“静区”，进而实现主动降噪。这种现象称为声波干扰消除[5]。

设入射声波为

p1=Acos(ωt-φ)

(1)

式中：p1表示瞬时声压值；A表示声压幅值；ω表示声波的频率；φ表示相位值。入射的平均声能密度E1为

(2)

式中：ρ表示介质的密度；c表示声波在空气中的传播速度；A表示声波的振幅。次级声信号p2为：

p2=βAcos(ωt-φ+α)

(3)

则叠加后的声能密度E2为：

(4)

式中：α是2种声波之间的相位差；β是2种声波振幅的比值。则在空气中任意一点，叠加前后2种声波之间的声级差Δ为：

(5)

由式(5)可知，当2种声波的振幅相同时，β趋近1，2种声波具有相反的相位，即α接近π时，由于与次级声信号相互抵消，初级噪声信号被大大衰减，即ANC技术的理论基础。

1.2 噪声主动控制算法

1.2.1最小均方算法

在实践中，很难直接计算自相关矩阵来获得最优权重系数，通常采用最小均方(LMS)算法[6-7]获得最佳权重系数。LMS算法是一种简单、有效的递推方法。基于最小均方误差算法的自适应滤波原理如图1所示。

图1 自适应滤波原理框图

LMS算法的目标函数表示为：

J(n)=E[e2(n)]=E[(d(n)-y(n))2]

(6)

式中：y(n)为输出信号；d(n) 为期望信号；e(n) 为误差信号。n时刻滤波器的输出可表示为y(n)。

(7)

将式(7)代入式(6)得到：

J(n)=E[(d(n)-WTX(n))2]

(8)

其中：

e2(n)=(d(n)-WT(n)X(n))*

(d(n)-WT(n)X(n))T

(9)

将式(9)代入式(8)中，目标函数可表示为：

J(n)=E[d2(n)]-2WT(n)P+WT(n)QW(n)

(10)

式中，P是d(n)和X(n)之间的互相关矩阵，可表示为：

(11)

Q是X(n)的自相关矩阵，表示为：

Q=E[X(n)XT(n)]

(12)

根据式(10)，用▽(n)表示J(n)对W(n)求导后的梯度，表示为：

(13)

当式(13)等于0时，目标函数J(n)取得最小值，此时最佳权矢量W0为：

W0=Q-1P

(14)

采用最速下降法获得权系数的递推公式。按照这种方法，下一刻的权矢量W(n+1)等于当前的权矢量W(n)减去一个正比于梯度▽(n)的变化量，即：

W(n+1)=W(n)-μ▽(n)

(15)

式中，μ为收敛系数或收敛因子。

在实际应用中，为便于系统的实时实现，取单个误差样本的平方的梯度作为均方误差梯度的估计，即：

(16)

将式(11)代入式(10)，推导出迭代表达式为：

W(n+1)=W(n)+2μe(n)X(n)

(17)

1.2.2算法性能分析

由于LMS算法的权系数、迭代速度等受收敛系数的值影响，因此，μ的取值很关键。

式(17)可改写为：

W(n+1)=W(n)+2μX(n)[d(n)-XT(n)W(n)]=

W(n)+2μP-2μQW(n) =

[I-2μQ]W(n)+2μQW0

(18)

E[W(n+1)-W0]=[I-2μQ]E[W(n)-W0]

(19)

式中，Q为正定矩阵，可用对角矩阵表示为：

Q=AT∧A=A-1∧A

(20)

将V(n)代入式(19)，得到：

V(n)=W(n)-W0

(21)

E[V(n+1)]=A-1[I-2μ∧]AE[V(n)]

(22)

将矢量V(n)的初始值设为V(0),得到：

E[V(n)]=A-1[I-2μ∧]nAE[V(0)]

(23)

式(23)的收敛条件为：

|1-2μλmax|<1

(24)

式中λmax为最大特征值，算法稳定条件为：

(25)

通常，用正定矩阵Q的迹表示收敛条件：

(26)

收敛因子μ过小会降低系统的收敛速度，过大会产生大的权矢量噪声，进而导致失调量增大。因此，选择合适的μ值可以保证系统稳定。进一步地，通过分析发现收敛速度是影响LMS算法性能的一个重要因素。

2 基于卷积神经网络的路面图像识别

2.1 VGG16神经网络

VGG16是一种简洁且高效的神经网络结构[8-11]，如图2所示。相比于AlexNet[12-14],VGG16采用几个小的卷积核(例如3*3卷积核)替代AlexNet中较大的卷积核(例如5*5和7*7的卷积核)提高神经网络的训练效果。

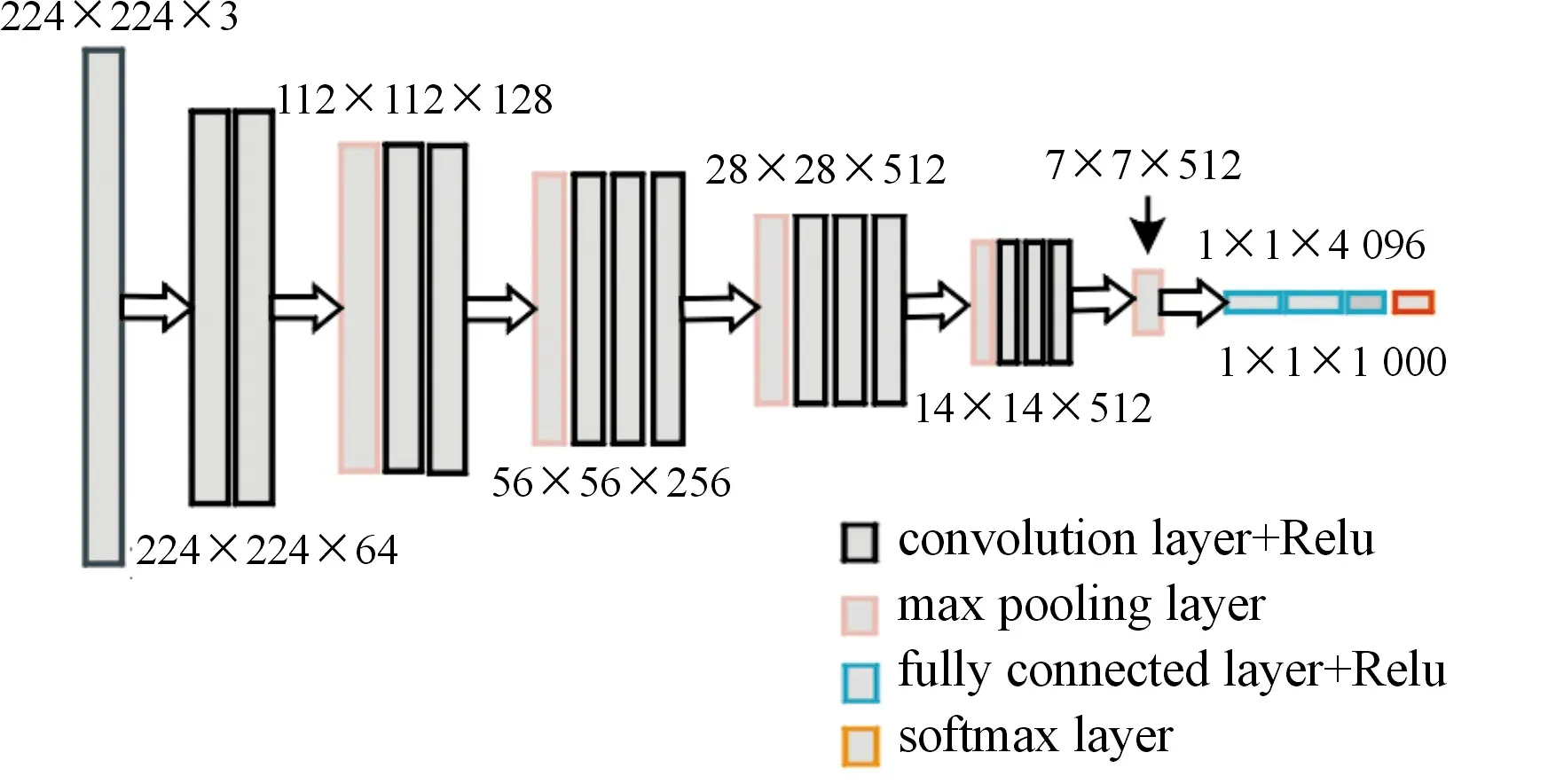
图2 VGG16网络结构示意图

VGG16中，卷积层用于提取图像特征。式(27)～(29)表示卷积层的特征提取过程。式中：a(l)是第l层的中间结果；a(l)是l层经过激活函数处理后的值。l+1层中包含用作l+1层输入a(l)的第l层的输出，权重W(l)、偏置b(l)、激活函数f、中间结果z(l+1)和输出a(l+1)。一般情况下，卷积层需要使用激活函数来获得非线性表示，因为非线性表示相比线性表示具有更强的表达效果。激活函数是relu激活函数，如式(30)所示。卷积层的输入/输出数据称为特征图，卷积层进行卷积运算，卷积运算相当于图像处理中的“滤波器运算”。

z(l)=W(l)+b(l)

(27)

⋮

z(l+1)=W(l)a(l)+b(l)

(28)

a(y)(l+1)=f(z(l+1))

(29)

(30)

池化层是缩小长、高方向上的空间运算，能够缩小空间大小，分为最大池化和平均池化。

全连接层把通过卷积层和池化层获得的特征结果映射到样本的标记空间，得到分类结果并输出。使用softmax分类器实现分类，softmax定义为

(31)

其中：S表示样本x是某一类的概率；ai表示分类器前一级的输出；C表示类别的数量。softmax将多分类输出转换为概率。

2.2 VGG16迁移学习模型

运用迁移学习的方法可将从其他领域学到的知识应用到所需的研究领域。比如，在训练神经网络的过程时，需要大量的样本对模型进行训练和优化。但是，即使有足够的样本，处理样本数据也是一个复杂的过程。迁移学习法可以弥补数据不足或训练时间不足、时间过长造成的问题。

VGG16卷积神经网络具有深层网络结构，可以提取和精炼图形中的特征。在开始时，卷积层只提取图像特征，在网络层较深时才处理特定任务。因此，在迁移学习[15]过程中，可将预处理过的模型应用于源域，保留下层的权值，只训练上层，并微调相关参数。根据不同特征的源域数据分布，利用目标域数据集微调模型，去掉原有的顶层，增加新的输出层，并增加softmax函数分类新问题。图3显示了卷积神经网络模型的迁移过程。通过对源域(自然图像)的训练权值进行迁移，对目标域(任务数据)进行微调，极大简化了模型在新域问题中的训练过程。

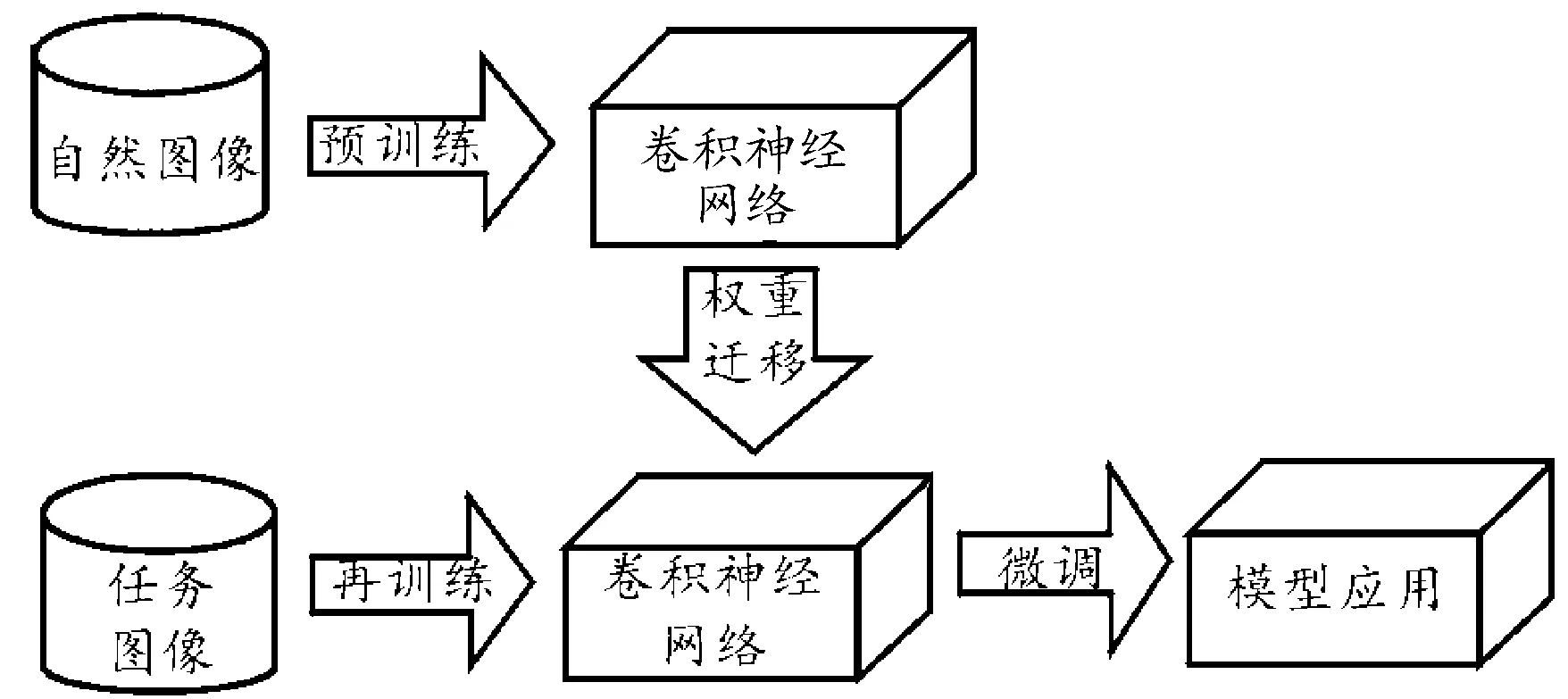
图3 卷积神经网络模型迁移过程示意图

2.3 数据集制作过程

1) 图片采集：使用摄像头采集路面图片，摄像头为单目变焦摄像头(如图4所示)。采集的路面图片可以分为3类，即3种不同粗糙度的路面。

图4 单目摄像头实物图片

2) 对采集到的3种不同类型的路面图片进行筛选，留下有用图片，并对筛选后的图片进行裁剪，得到所需图片中的主体部分；再对图片进行排序编号，放入分类好的文件夹中。

2.4 数据预处理与增强

首先将采集的路面图片按照粗糙程度不同分为3类，剔除模糊不清的数据。剔除后的数据样本总量为1 000张图片，按照7∶2∶1的比例，把所有有用图像分为训练集、验证集和测试集。随之进行数据增强与扩充，将路面图像随机旋转30°，水平方向和垂直方向随机平移30%。对图像进行随机水平翻转，并将图像随机缩放的幅度设置为0.5。最后，将所有路面图像调整为224×224像素，对作为输入层的图像进行批量归一化(batch normalization,BN)处理。BN处理不仅可以有效缓解梯度消失问题，还可以增强网络的泛化能力和收敛速度。

3 模型训练与结果分析

3.1 模型训练

实验硬件环境：CPU为 Intel(R)Core(TM)i5-10300H CPU @2.50GHz；GPU为NVIDIA GeForce RTX 2070；深度学习框架为VGG16。

把采集的路面图像放入VGG16网络模型中进行训练，模型的优化算法采用随机梯度下降(stochastic gradient descent,SGD)算法。设SGD优化器初始学习率为0.000 1，最小批量值(mini-batch size)设置为10，验证频率(validation frequency)设置为3。模型训练的损失函数是交叉熵损失函数，最后将epoch值设置为200开始进行训练。

3.2 结果分析

分析图5的训练集与验证集的准确率、损失率曲线可知，在经过约50次迭代后，模型趋近收敛，且曲线的趋势基本重合。准确率曲线在数值上接近1，损失率曲线接近于0。训练结束后，通过编写代码，从路面图片的验证集中随机抽取6个图片导入训练好的网络模型中。从6个路面图片中选取3张不同路面类型的图片，识别效果见图6，每个路面图片上方显示了验证结果和准确率。可以发现，通过摄像头采集的3种路面，完成训练的CNN具有良好的识别效果和泛化能力。

图5 VGG16训练和验证结果曲线

图6 验证结果和准确率场景图

4 仿真分析

4.1 路噪主动控制流程

路面识别和路噪主动控制的过程(见图7)由路面图像采集、路面类型识别和路噪主动控制3部分组成。从图7可以看出:首先，路面图像由摄像头采集，作为CNN的输入；其次，CNN通过预训练识别输入图像；最后，根据识别结果选择相应路面下路噪主动控制系统的收敛因子，实现车辆在不同道路下的调整，达到减小车辆路面噪声的目的。对3种不同类型路面进行仿真分析，比较3种路面的原始噪声和3种路面收敛因子取中间值以及根据不同类型路面调整收敛因子后的降噪效果。

图7 基于路面识别的路噪主动控制流程框图

4.2 3种路面仿真结果

为保证车辆在不同类型的路面行驶时具有良好的舒适性，需对路噪主动控制系统调整收敛因子，找到各个路面对应的最优收敛因子，使其在不同路面类型下达到最优的降噪效果。根据所建立的路噪主动控制模型，以LMS算法收敛因子为优化变量，以路面噪声为优化目标。根据LMS算法的收敛特性，不同工况条件下最优收敛因子不同，故针对不同路面，使用不同收敛因子进行大量仿真，通过观测控制效果预标定本系统在3种不同路面工况下的最优收敛因子值。针对不同的路面激励，经过前期大量的筛选，选出接近最优降噪效果的3种收敛因子，比较分析得出最优收敛因子，获得当前路面噪声的最优降噪效果。以某车型在不同路面采集的原始噪声作为参照，得到仿真结果如图8所示。

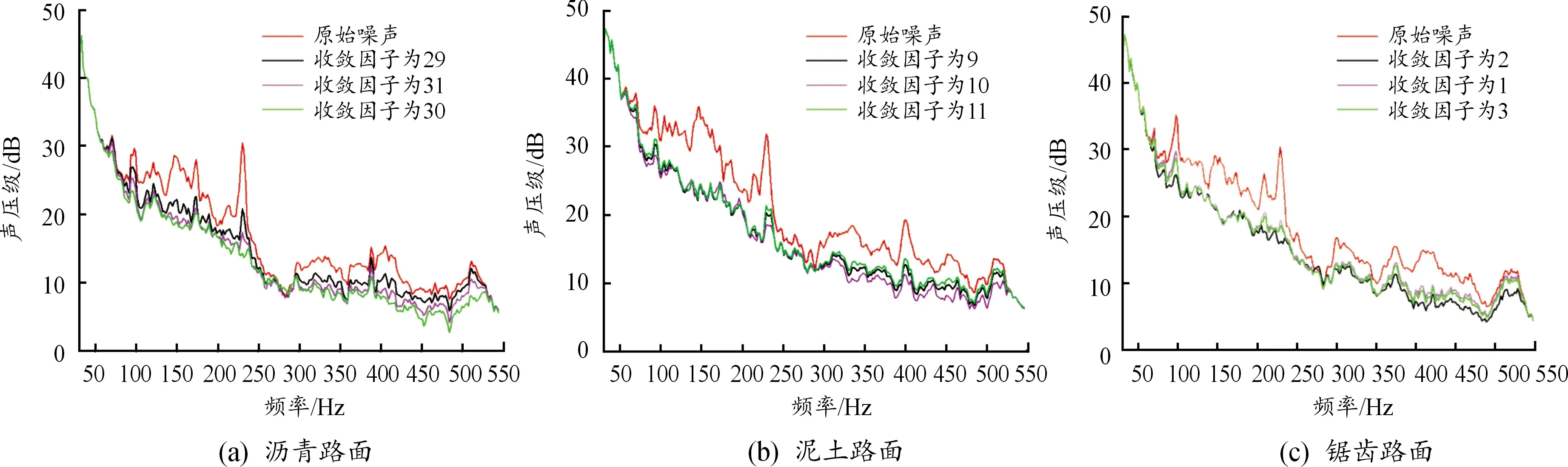
图8 不同路面类型时各收敛因子降噪效果曲线

在建立的仿真模型中，采样时间设定为30 s，采样频率设定为2 000 Hz，控制滤波器选用常用的有限脉冲响应FIR滤波器；模型输入为60 km/h下采集的不同路面噪声信号，模型输出为头枕处扬声器发出的次级信号。由图8得到各路面降噪效果如下：

1) 在60 km/h的沥青路面,80～550 Hz频带范围内，当收敛因子取31时的平均降噪量为2.5 dB，频率为230 Hz处的峰值降噪量为6.4 dB；当收敛因子取29时，平均降噪量为3.7 dB，在频率230 Hz处的峰值降噪量为13.2 dB；当收敛因子取30时，平均降噪量为4.3 dB，在频率230 Hz处的峰值降噪量可以达到16.3dB。

2) 在60 km/h的泥土路面下，80～550 Hz频带范围内，当收敛因子取9时的平均降噪量为4.6 dB，频率225Hz处的峰值降噪量为11.5 dB；当收敛因子为11时，平均降噪量为4.15 dB，频率225 Hz处的峰值降噪量为10.4 dB；当收敛因子取10时，平均降噪量为5.1 dB，频率225 Hz处的峰值降噪量可以达到13.5 dB。

3) 在60 km/h的锯齿形路面下，80～550 Hz频带范围内，当收敛因子取1时的平均降噪量为3.3 dB，频率228 Hz处的峰值降噪量为10.9 dB；当收敛因子为3时，平均降噪量为3.7 dB,频率228 Hz处的峰值降噪量为12 dB；当收敛因子调整为2时，平均降噪量为4.3 dB，频率228 Hz处的峰值降噪量可以达到14.7 dB。

将上述3组降噪数据汇总得到表1，经分析发现：当车辆行驶在沥青路面时，调整收敛因子为30，取得的降噪效果最好；当车辆行驶在泥土路面时，调整收敛因子为10，降噪效果最好；当车辆行驶在锯齿路面时，调整收敛因子为2，取得的降噪效果最好。

表1 各种路面类型时不同收敛因子的降噪量

对比表1中的平均降噪量数据，得到不同路面类型下的最优收敛因子。在已建立的仿真模型中加入路面预判，以路面图片作为输入，在已训练好的卷积神经网络中进行分类，从而识别路面类型，对应该路面下的最优收敛因子，获得降噪效果。取3种路面最优收敛因子的中间值，以获得3种路面取同一收敛因子时的降噪效果。统一与路面无控制的原始噪声进行对比，得到仿真结果(见图9)。

图9 不同路面类型下优化前后降噪效果曲线

分析表2中各路面类型优化前后的降噪量可发现：当路噪主动控制系统在不同路面类型下只选取相同的1个收敛因子时，不能保证在所有路面类型下都取得最好的降噪效果。即在不同路面类型下取1个相同的收敛因子时，其降噪效果低于预判路面类型，故不同路面下应选取该路面对应的最优收敛因子，以获得最佳效果。

表2 各路面优化前后降噪量

5 结论

1) 在模型训练过程中，可通过数据批量归一化和数据增强两种措施来增强网络的收敛速度和泛化能力。

2) 运用卷积神经网络的路面识别方法可以准确识别采集到的3种不同类型路面。

3) 基于路面识别的路噪主动控制系统可根据不同路面类型调整收敛因子，提升车辆在不同路面的噪声优化效果。