含分布式电源的复杂配电网相间故障定位等效解耦模型

白星振，宋昭杉，葛磊蛟，张波，朱爱莲，牛峰

(1.山东科技大学电气与自动化工程学院，山东省青岛市266590；2. 智能电网教育部重点实验室(天津大学)，天津市300072；3.中国人民解放军32654部队，济南市250024；4. 青岛龙发热电有限公司，山东省青岛市 266317；5. 省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学)，天津市300130)

0 引 言

分布式电源(distributed generation，DG)规模化接入，使配电网的结构由辐射状变为电源与用户互联的复杂多源网络[1-3]，因此基于传统矩阵算法的配电网故障定位方法已经不再适用。然而，近年来，随着分布式电源、电动汽车等技术的持续迅猛发展，智能配电网进一步呈现出结构复杂、运行多态、故障场景多的特点，致使局部、连锁、跨区等故障特征逐渐多样化，且精准定位难度增加。为实现配电网可靠高效运行，非常有必要重新深入研究含分布式电源的配电网相间故障定位方法[4-6]。

针对含分布式电源的配电网故障定位，国内外学者提出了一些方法，如矩阵算法[7]、优化算法[8]和基于人工神经网络[9]的方法等，其中矩阵算法因运算速度快、算法方便等优点被广泛使用。矩阵算法是通过馈线终端单元(feeder terminal unit，FTU)上传的过流告警信息建立告警信息矩阵，结合配电网拓扑结构矩阵建立区段判别的异或逻辑，实现配电网故障定位。文献[10]中提出的矩阵算法能够实现对多电源配电网的故障定位，但该方法需要根据电源位置多次假定正方向，计算复杂、耗时长。文献[11]提出的故障定位改进矩阵算法通过矩阵间的运算并结合故障判据，即可实现对配电网故障的精确定位，但该方法中提出的故障判据较为复杂，难以直接实现故障区段的定位。文献[12]提出了一种基于可达矩阵的配电网故障定位方法，通过可达矩阵与故障信息矩阵的运算可直接实现故障定位，但该方法对于多重故障的定位需要进行多次重复运算，降低了故障定位的效率。文献[13]提出了一种含分布式电源的环形配电网故障定位算法，在只定义一次正方向的前提下即可实现故障的精确定位，但该方法并未考虑到混合型拓扑结构的复杂配电网，且该矩阵算法过程较为复杂，计算效率不高。

配电网结构复杂多样，主要包括放射型、环型、多分段多联络型等，当配电网结构较为复杂时，矩阵算法往往存在以下问题：1) 配电网结构复杂导致故障电流方向难以确定，故障信息矩阵难以建立；2) 配电网节点、支路众多导致的矩阵维数较大，浪费大量存储空间；3) 矩阵间的计算复杂，导致矩阵算法计算量大、计算速度慢，出现“维数灾”等问题[14]，效率大大降低。为此，文献[15]提出了一种将配电网复杂结构等效解耦的方法，减少了配电网拓扑结构矩阵占据的存储空间，大大加快了运算速度，但文中并未考虑多种拓扑结构混合以及多电源配电网的等效解耦。

针对上述问题，本文提出一种基于等效解耦的配电网故障定位改进矩阵算法。首先，基于深度优先原则对复杂配电网进行等效解耦，避免配电网因结构复杂而导致的矩阵建立困难等问题；进一步，对解耦后的各支路分别建立因果关联矩阵、故障信息矩阵，通过矩阵运算和重组分析即可直接实现故障区段的定位。仿真结果表明，本文所提出的方法无需故障判据即可实现故障区段的准确定位，与传统故障定位方法相比，本文方法矩阵建立方便、计算量小、故障定位时间短，有效提高配电网故障定位矩阵算法的实用性。

1 分布式电源接入对故障定位的影响

分布式电源的接入，使得配电网由传统的辐射状网络变为多电源和用户互联的复杂网络。与传统配电网相比，故障状态下，主电源和分布式电源会同时向故障点提供故障电流，配电网中同时出现了正向和反向故障电流，传统矩阵算法中由于未考虑分布式电源的接入，未对反向故障电流进行定义，因此已不再适用。以图1为例，当区段L1发生故障时，配电网中电流方向如图所示，其中，馈线开关S1流过的电流方向与馈线开关S2流过的电流方向相反，传统矩阵算法只对单一方向故障电流进行了定义，在该情况下无法实现故障定位。

图1 含分布式电源的简单配电网模型Fig.1 Simple distribution network model with distributed power

在实现故障定位的过程中，传统矩阵算法往往需要对配电网中的电源多次假定潮流正方向[16]，再结合故障判据经过多次计算实现定位，计算过程繁琐；同时，传统矩阵算法往往会出现T型区域以及馈线末端区域定位失败的问题。因此，对于含分布式电源配电网的故障定位问题，传统矩阵算法已经不再适用。

2 复杂配电网的等效解耦算法

2.1 配电网等效解耦原则

针对复杂配电网拓扑结构种类繁杂、节点众多、矩阵难以建立的问题，本文基于深度优先原则，提出了基于关联矩阵的配电网等效解耦算法，将复杂配电网解耦为多个树干状网络。与其他拓扑结构相比，树干状结构配电网从电源点到其他任何一个节点的路径都是单一的，便于分析故障电流，大大提高了矩阵建立的效率。

复杂配电网等效解耦算法中，选定一个正常状态的主电源始终作为解耦后树干状网络的起点，其余电源或负荷馈线端作为树干状网络的终点，通过配电网邻接矩阵寻找从主电源到其余电源或负荷的唯一路径。

2.2 配电网等效解耦实现

图论作为离散数学的一个重要分支，在互联网、电力系统等多个行业中得到了广泛应用[17-19]。它以表征事物间特殊关系的图形作为研究对象，一般用点代表事物，用两点之间的连接线表示两个事物间的特定关系。

配电网等效解耦算法基于上述图论思想，将配电网中的隔离开关等效为节点，开关之间的馈线等效为边。对含有n个开关的配电网，定义其关联矩阵元素如下：

(1)

式中：Dij表示区段Lj和开关Si的关联关系。

为更清楚地描述配电网等效解耦算法，本文以图2中等效解耦前配电网为例，建立关联矩阵：

(2)

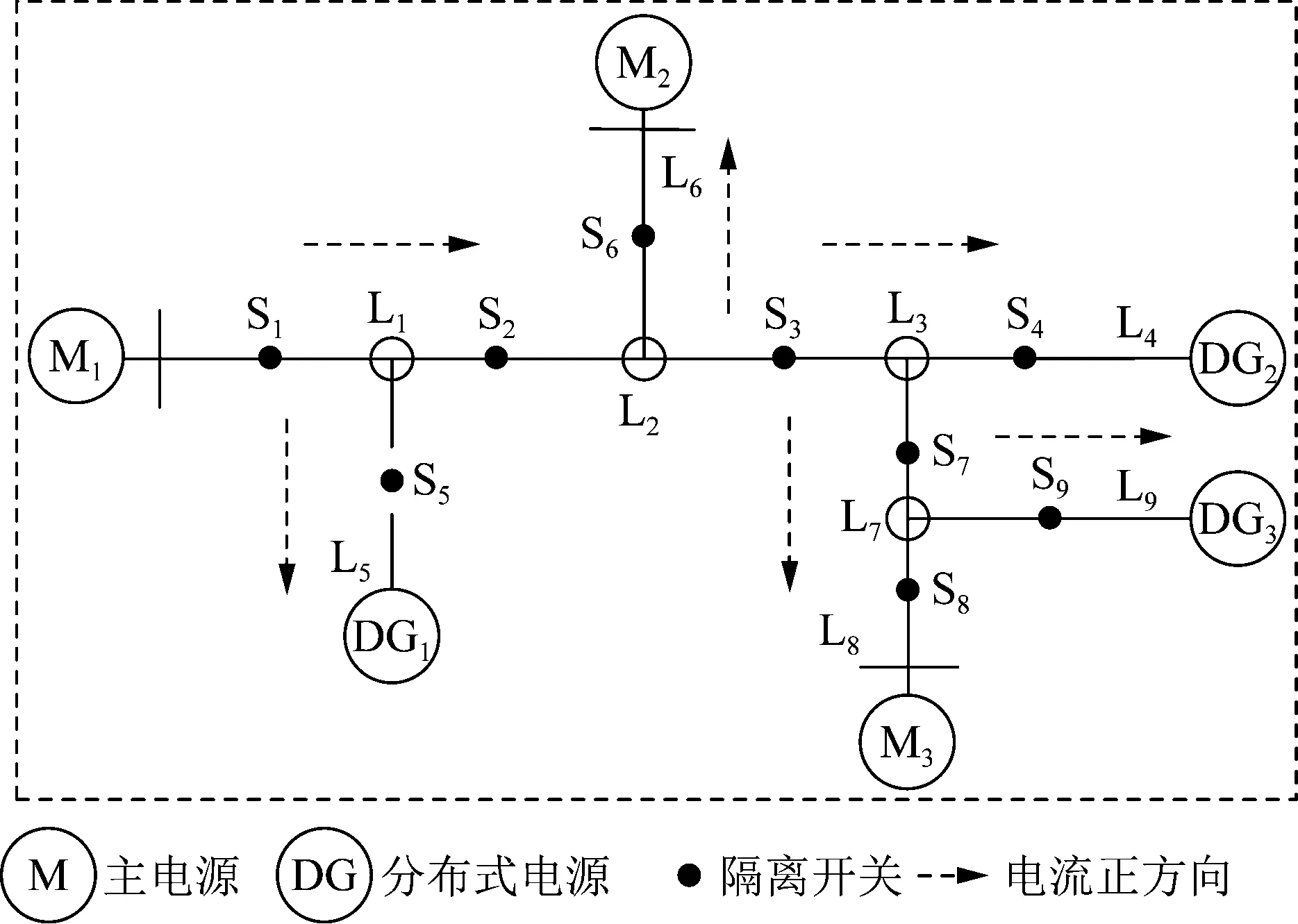
图2 复杂配电网模型Fig.2 Complex distribution network model

基于上述矩阵，配电网等效解耦方法如下：

步骤1：按列对矩阵D中元素进行搜索，寻找只含一个元素为1的列，记该列编号为li；

步骤2：将编号li存入矩阵Ni中，记作Ni=[li]；

步骤3：搜索li行中除主对角线元素外值为1的元素，将该元素所在列数记作ki；

步骤4：将编号ki存入矩阵Ni中，记作Ni=[kili]；

步骤5：验证ki是否为1，若ki=1，则输出矩阵Ni；否则令li=ki,重复步骤3至步骤5，直至满足条件为止。

本文以图2为例，对上述流程进行说明：

步骤1：搜索矩阵D中各列元素，找到只存在一个元素为1的列数，矩阵D中满足条件的共有5列，分别记作l1=9、l2=8、l3=6、l4=5、l5=5；

步骤2：以l1=9为例，将编号l1=9存入矩阵N1中，得到N1=[9]；

步骤3：搜索矩阵D中第9行中除对角线元素值为1的元素，可得D97=1，则k1=7；

步骤4：将k1=7存入矩阵N1中，此时N1=[7 9]；

步骤5：k1=7≠1，则令li=ki=7，继续进行搜索；

步骤6：重复上述步骤继续搜索，最后得到N1=[1 2 3 7 9]，即可得配电网解耦后的一条支路，其余支路分别为N2=[1 2 3 7 8]、N3=[1 2 3 4]、N4=[1 2 6]、N1=[1 5]。图2所示复杂配电网的等效解耦结果如图3所示。

图3 等效解耦结果Fig.3 Equivalent decoupling results

3 故障定位改进矩阵算法

故障定位矩阵算法基于图论思想将配电网中的馈线开关等效为节点，将开关之间的馈线等效为边，通过拓扑结构矩阵与故障信息矩阵，并结合故障判据实现故障定位。对于含分布式电源的配电网，传统矩阵算法需要多次定义电源正方向并进行多次判断，计算过程繁琐；并且对于含有分支的区段和馈线末梢区段可能出现定位失败的问题。针对上述问题，本文提出了配电网故障定位改进矩阵算法。与传统矩阵算法中采用的拓扑结构矩阵不同，本算法对于含有n个开关，m条馈线的配电网，定义n×m维因果关联矩阵B第i行第j列元素如下：

(3)

其中，对于任意含分布式电源的配电网，规定某个主电源到其余各电源或馈线终端的方向为电流的正方向。

根据故障时配电网各开关上FTU所传递的告警信息，定义n×1维故障信息矩阵F，其中的元素分别对应各开关上流过的信息，第i个元素Fi1定义如下：

(4)

其中，故障信息矩阵F中电流正方向与因果关联矩阵B中电流正方向的定义相同，均为某个主电源到其余各电源或馈线终端的方向。

东方宇轩坐在堂上，静穆威严，哪里有一星半点当日戴面具扮黄梁村老黄的滑稽模样，左右分别是药圣孙思邈、工圣僧一行、书圣颜真卿、棋圣王积薪、画圣林白轩、琴圣苏雨鸾，连平素不太露面的乌有先生、子虚道人两位客卿也俨俨然敬陪在末座上。宇晴笑着与众人打招呼：“你们这里神佛菩萨一般坐着，着我去拘这三个孩子，已经带来了，你们仔细考问，别将人家孩子吓着。”说完坐到苏雨鸾旁边为她留出的座位，只剩下袁安、上官星雨、李离三个家伙在门槛前面被灯火皇皇照亮的空地上，呆头呆脑地站着。

与上述矩阵相对应，建立表征各馈线状态的m×1维状态信息矩阵S，矩阵中的元素表示开关之间馈线的运行状态，第j个元素Sj1定义如下：

(5)

考虑到上述矩阵之间的关系，本文定义了逻辑化运算Z=：若矩阵Z与X维数相同，则当Xij>0时，Zij=1；否则Zij=0。基于以上定义，本文通过计算得到馈线状态信息矩阵：

S=

(6)

根据信息状态矩阵S中元素的定义即可实现故障区段的精确定位。

与传统矩阵算法相比，本文提出的改进矩阵算法只需定义一次潮流正方向，即可直接实现故障区段的精确定位，无需结合故障判据；且当配电网出现多重故障时，通过改进矩阵算法可以一次性实现全部故障区段的定位，无需重复计算，效率大大提高。

本文以图2为例，假定区段L2与L4发生故障，对等效解耦后的配电网采用改进矩阵算法进行故障定位，根据定义对解耦后的支路3树干状网络建立因果关联矩阵与故障信息矩阵，其余支路的建立与支路3同理。

(3)

式中：B3为支路3的因果关联矩阵。

(8)

式中：F3为支路3的故障信息矩阵。

由上述矩阵计算可得：

(9)

结合馈线状态信息矩阵定义可得，区段L2与L4发生故障，与假定的故障区段一致，验证了改进矩阵算法的有效性。

对于复杂配电网，经过等效解耦后，应用本文提出的改进矩阵算法对解耦后的树干状网络进行故障定位，将得到的结果取并集即可得到解耦前配电网的故障位置。实现故障定位后，对故障定位结果进行校验，若配电系统恢复正常供电，则结束故障定位；否则，排除上述故障后，使用改进矩阵算法进行二次定位，直到恢复配电网正常供电为止。仍以图2为例，假定区段L2与L4发生故障，对5条支路进行故障定位得到的结果分别为：

R1=∅

(10)

R2=R4=R5={L2}

(11)

R3={L2,L4}

(12)

式中：Ri(i=1,2,3,4,5)表示第i条支路的故障区段集合，其中，R1=∅表示等效解耦后的第1支路未发生故障，R2=R4=R5={L2}表示解耦后第2、4、5条支路故障发生在L2区段，R3={L2，L4}表示解耦后第3条支路故障发生在L2、L4区段。

对上述结果取并集可得：

R=R1∪R2∪…∪R5={L2,L4}

(13)

因此故障解耦前复杂配电网故障发生在L2与L4区段，校验后与原假设相同，即成功实现故障定位。

本文提出的故障定位方法流程如图4所示。

图4 故障定位算法流程Fig.4 Flowchart of fault-location algorithm

4 仿真分析

为验证上文提出的故障定位算法的有效性，本文分别以北方一个园区实际的智能配电网和改进IEEE 33节点配电网模型分别进行测试。在解耦前的配电网模型中分别设置不同数量和位置的故障，通过本文的解耦算法与改进矩阵算法进行故障定位。

4.1 改进IEEE 33节点系统测试

本文以含分布式电源的改进IEEE 33节点配电网模型进行分析。其中M1为主电源，DG1—DG4表示配电网中接入的分布式电源，K1—K4分别为分布式电源的投切系数，Ki=1(i=1,2,3,4)表示分布式电源接入配电网，Ki=0(i=1,2,3,4)表示分布式电源未接入配电网。本文分别在不同的投切系数下对改进IEEE 33节点系统设置不同故障，验证本文所提出方法的有效性。

根据上文提出的方法，首先对IEEE 33节点系统进行等效解耦，解耦前后如图5所示。

图5 改进IEEE 33节点配电网等效解耦Fig.5 Equivalent decoupling of improved IEEE 33-node distribution network

本文针对解耦前的改进IEEE 33节点配电网系统分别设置了不同数量和位置的故障，并在不同的投切系数下对解耦后的各支路分别采用改进矩阵算法进行故障定位，结果如表1所示。根据表1中的结果分析可得：

1)针对不同数量的故障，本文提出的算法在改进IEEE 33节点配电网中能够实现故障的精确定位。

2)对比表1中故障1、2和3、4可得，在不同投切系数下，应用本文提出的算法均能实现故障的准确定位，即不同分布式电源的投切对故障定位的结果没有影响。

3)本文所提出的算法能够正确定位区段L23的故障，即能够实现对配电网末梢区段的故障定位。

4.2 典型园区配电网模型测试

由于改进IEEE 33节点配电网只包含放射型拓扑结构，并不能完全体现配电网结构复杂的特征。为此，本文以北方某园区实际的智能配电网为例，配电网中包含放射型、环型、多分段多联络型拓扑结构，结合本文算法对配电网中的故障进行定位，如图6所示。该系统包含3个主电源与3个分布式电源、20个隔离开关和2个联络开关。

可以看出，该典型园区配电网模型由于包含多种拓扑结构变得十分复杂，采用矩阵算法直接故障定位会使因果关联矩阵的建立变得十分复杂，导致故障定位计算量增大。因此首先对其进行等效解耦，解耦过程如图6所示。

表1 不同投切系数下IEEE 33节点配电网故障定位结果Table 1 Fault location results of IEEE 33-node distribution network with different switching coefficients

图6 复杂配电网等效解耦实现Fig.6 Implementation of equivalent decoupling for complex distribution network

首先，针对图6中解耦前的复杂配电网，设置不同位置和数量的故障；接着，采用本文所提出的改进矩阵算法，对解耦后的各支路进行故障定位，得到的结果如表2所示。根据表2中的结果分析可得：

1)对于配电网中不同位置和数量的故障，应用本文所提出的算法能够实现精确定位。

2)由表2中故障8分析结果可知，当故障发生在区段L2、 L5、 L7、 L10时，仅使用一次改进矩阵算法无法实现区段L5的故障定位，需要进行校验，并在排除一次故障定位结果后进行第二次故障定位即可实现全部故障区段的准确定位。

3)对于多种拓扑结构混合的配电网，本文所提出的等效解耦算法能够对配电网进行简化，结合矩阵算法实现了故障的准确定位，即在配电网拓扑结构复杂的情况下，应用本文算法仍能有效实现故障区段的定位。

表2 复杂配电网故障定位结果Table 2 Fault location results for complex distribution network

4.3 性能分析

为体现基于等效解耦的改进矩阵算法的优势，本文分别将该算法与行波法、文献[10]和文献[12]中所提出的矩阵算法进行比较，所有算例均在2.60 GHz双核处理器，16 GB内存的计算机上，利用MATLAB编程实现。通过对算法计算时间、故障定位精度等指标的对比分析，验证本文所提出算法的优势。

本文首先在改进IEEE 33节点系统中分别进行不同矩阵算法的模拟，假定区段L2、L23、L28和L31发生故障，分别根据不同算法建立相关矩阵进行故障定位，并比较不同算法的故障定位时间、精度和矩阵的维数，对比结果如表3所示。应当注意的是，采用矩阵算法实现故障定位的时间包括三部分：1)FTU利用自身算法检测到故障的时间，本文定义该时间为100 ms；2)向数据采集与监视控制(supervisory control and data acquisition，SCADA)系统通信的延时，本文定义该时间为100 ms；3)SCADA系统利用矩阵算法实现故障区段定位所需时间，即算法运行时间。

由表3结果对比分析可得以下结论：

1)应用本文所提出的故障定位方法只需204.345 ms即可确定故障位置，与其他矩阵算法相比故障定位速度更快。

表3 改进IEEE 33节点系统下不同矩阵算法的比较Table 3 Comparison of different matrix algorithms under improved IEEE 33-node system

2)与文献[10]、文献[12]中所提出的方法相比，本文方法在矩阵的建立上虽然数量变多，但维数均有所减少，在矩阵运算过程中避免了“维数灾”现象的出现；且等效解耦后的支路均为树干状网络，故障电流分析更加方便。同理，若仅采用改进矩阵算法进行故障定位，复杂配电网模型会导致因果关联矩阵建立复杂、故障电流难以分析，随着配电网中节点数量的增加，矩阵维数也会增加，降低了故障定位的效率。

3)本文所提出的算法与基于可达矩阵的故障定位方法均无需结合故障判据即可实现故障区段的定位；与传统矩阵算法相比，本文方法在T型支路上的定位精确度更高，而传统矩阵算法在该支路的定位中会出现部分漏判的情况。

4)应用本文算法实现故障的精确定位仅需迭代2次，降低了算法的复杂程度，相比之下，其他算法需要更多次数的迭代。

此外，为验证本文算法在更加复杂的系统中也具有定位时间较短的优势，本文在IEEE 69节点系统中进行3种矩阵算法的对比，假定区段L6、L17、L24、L54、L63、L67均发生故障，如图7所示。采用不同的矩阵算法进行故障定位，并比较定位时间，结果如表4所示。

图7 IEEE 69节点配电网模型Fig.7 IEEE 69-node distribution network model

表4 IEEE 69节点系统下不同算法定位时间对比Table 4 Comparison of different algorithms in IEEE 69-node system

对比表4中的结果可以看出，由于系统节点以及故障数量的增加，3种矩阵算法在IEEE 69节点系统中相较于改进IEEE 33节点系统定位时间均有所增加，但本文所提出的算法在IEEE 69节点系统中定位时间仍较短，仅为0.037 s，验证了本文算法在不同系统中均具有故障定位速度快的优势。

当故障发生时，快速的故障定位能够有效减少停电面积。为此本文利用改进矩阵算法与行波法在图8系统中进行故障定位，对定位时间进行比较。假定图8中各节点之间线路长度均为100 km，行波速度为2.932 9×105km/s[20]。在距离电源M1100 km处设置故障，即区段L1处发生故障。故障定位对比结果如表5所示。

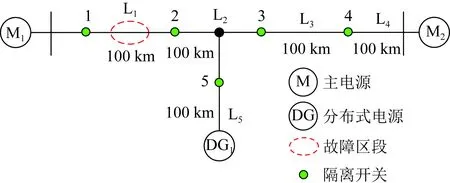
图8 对比算法配电网模型Fig.8 Distribution network model with comparison algorithm

表5 不同算法故障定位时间和效果比较Table 5 Comparison of different algorithms

由表5对比分析可知，本文所提出的改进矩阵算法只能定位至故障发生的区段，而行波法可以实现故障具体位置的定位，精度更高；但本文所提出的改进矩阵算法在故障定位时间上更短，能够大大减少配电网中用户侧的停电面积。

5 结 论

本文提出了一种基于等效解耦模型的改进故障定位矩阵算法。通过对含分布式电源的复杂配电网的等效解耦简化了配电网拓扑结构，基于等效解耦模型提出的改进矩阵算法，能够一次性实现多个区段故障的定位，大大减少了矩阵算法的计算量，节省了故障定位的时间，减少了用户侧的停电面积。仿真结果表明，本文所提出的算法在复杂配电网和改进IEEE 33节点系统中均能实现故障的准确定位，且相较于行波法与其他矩阵算法，该方法故障定位时间较短，能够有效减小用户侧停电面积。

未来的工作将在本文方法的基础上，针对FTU信息畸变、漏报等问题进行研究，以期进一步实现故障区段的准确定位。