基于纳什谈判的共享储能电站优化运行研究

黄铖，刘海涛,2，马丙泰，陆恒

(1. 南京工程学院电力工程学院，南京市 211167；2. 江苏省配电网智能技术与装备协同创新中心，南京市 211167)

0 引 言

随着全球对能源危机的高度关注，风电、光伏等可再生能源发电得到了广泛的应用[1-2]。但是随着可再生能源装机容量及渗透率的不断提高，电力系统的稳定运行受到挑战，并造成大比例的弃风、弃光，而储能是解决可再生能源消纳问题的最佳途径之一[3-4]。

随着分布式储能的发展，共享储能经济模式受到越来越多的关注。目前，国内外已有对共享储能的研究，文献[5]提出了一种基于“共享储能和需求侧资源”的市场化消费模型，通过算例分析证实其可以促进可再生能源的消纳。文献[6]提出了基于Stackelberg博弈的共享储能社区微电网能源管理模型，并通过模拟退火算法验证了其有效性。为了降低用户群的用能费用，文献[7]建立了以用户群经济性最优为目标的综合能源系统协同优化模型。为了分析输电成本和网损对博弈结果的影响，文献[8]提出了发电侧共享储能规划模型。文献[9]利用鲁棒优化算法，求解了工业园区共享储能配置的双层优化模型。文献[10]提出了一种多区域综合能源系统互联下的共享储能系统容量优化配置模型，算例表明其可以降低系统运行成本，优化共享储能系统参数。文献[11]提出了多微能源网共享储能电站的服务模式，通过对比不配置储能、单独配置储能的场景，突出共享储能的优越性。文献[12]分析了居民社区使用共享储能的实际效益。

共享储能涉及多个控制主体间的优化调度，而现实中发电站、储能电站以及各个用户主体之间都是不同的利益主体，彼此之间没有信息交互，都以自身利益最大化为目标，这会造成市场的无序竞争，降低市场的效率。因此常采用合作博弈和非合作博弈理论来解决多主体之间的利益分配问题[13]。非合作博弈指多主体在利益相互影响的过程中如何决策使自身利益最大化，强调个体理性。例如文献[14]采用非合作博弈理论提出了以各能源系统成本最小为目标的综合能源优化调度模型。而合作博弈强调的是团体理性，兼顾个体利益和整体利益。纳什谈判理论属于合作博弈范畴，用于解决多主体间的利益均衡分配问题。文献[15]提出了风光氢多主体能源系统的纳什谈判合作优化模型，并利用交替方向乘子法(alternating direction method of multipliers, ADMM)求解。文献[16-18]介绍了基于纳什谈判理论的多微网电能交易模型。文献[19]考虑了市场价格、可再生能源和综合需求响应的不确定性，提出了基于纳什谈判的综合能源交易模型。文献[20]设计了一个基于纳什议价的能源交易市场。

本文将针对共享储能电站和工业用户群的多主体合作模型进行研究，分析整个系统的主体收益情况。首先建立园区共享储能电站(park energy storage，PES)和工业用户的联合运行模型，然后建立其合作运行纳什谈判模型，并将此非线性问题转化为整个系统收益最大化和电能交易支付谈判2个子问题。最后通过交替方向乘子法来依次实现这2个子问题的分布式求解，并通过相关算例来证明其有效性。

1 考虑电能交易的多主体运行模型

典型共享储能电站虚拟示意如图1所示。在传统的多主体运行模式中，大多采用“自发自用，余电上网”的形式，而工业园区内的企业以工业电价向电网购电来满足工业用户的负荷需求。而通过共享储能电站，可以为一片园区或者同一配电区域内的众多用户提供共享服务，即用户可以不受时间和容量的限制进行充放电的需求[21]。根据用户使用共享储能电站的充放电量，用户需要向共享储能电站缴纳相应的费用。

图1 共享储能电站虚拟示意Fig.1 Virtual schematic diagram of shared energy-storage power station

1.1 共享储能电站运行模型

共享储能电站的交易对象包括外电网以及各个工业用户主体，其运行成本包括储能设备的充放电成本Cde，与外电网的交互成本Ctr1以及与用户之间的交互成本Cpu。共享储能电站的收益UPES可以表示为总运行成本的相反数，即PES的效益最大化运行模型为：

maxUPES=-(Cde+Ctr1+Cpu)

(1)

(2)

(3)

(4)

式中：T为调度周期；N为工业用户的个数；Pch(t)为t时段储能设备的充电量；Pdis(t)为t时段储能设备的放电量；τ为储能设备的运维成本系数；PS(t)为t时段共享储能电站向外电网的售电量；γ(t)为向电网的售电价格；Qe,i(t)为共享储能电站与工业用户i的交互电量(小于0为向用户购买电量，大于0为向用户销售电量)；δi(t)为用户i与共享储能电站之间的交互电价。

忽略设备损耗，共享储能电站的运行模型应满足的约束条件如下：

1)园区共享储能电站电功率平衡约束。

Pch(t)-Pdis(t)+PS(t)+Qe,i(t)=0

(5)

2)储能的充放电上下限约束。

(6)

式中：Pmax为共享储能电站的最大充放电功率。

3)与外电网交易量的非负性约束。

PS(t)≥0

(7)

4)共享储能电站荷电状态连续性约束。

SSOCmin≤SSOC(t)≤SSOCmax

(8)

(9)

式中：SSOC(t)为共享储能电站在t时段的荷电状态；SSOCmax、SSOCmin分别为共享储能电站荷电状态的上、下限；Emax为储能电站的最大容量；ηch、ηdis分别为共享储能电站的充、放电效率。

1.2 工业用户主体运行模型

工业用户主体考虑负荷的需求响应，调整用电计划，确定与外电网和园区共享储能电站之间的交互电量，并以运行成本最小为目标。其运行成本包括电负荷调整的不舒适成本Csl，与外电网的交互成本Ctr2以及与共享储能电站之间的交互成本C′pu。则工业用户主体i的效益Ui最大化模型为：

maxUi=-(Csl+Ctr2+C′pu)

(10)

Csl=c1|Ptran(t)|+c2|Pcut(t)|

(11)

(12)

(13)

式中：Ptran(t)为t时段可调整电负荷的量；Pcut(t)为t时段可削减电负荷的量；c1、c2分别为单位可调整负荷和可削减负荷的补偿成本；cTOU(t)为工业分时电价；Pb(t)为用户向外电网的购电量；Pe,i(t)为t时段用户i与共享储能电站的交互电量(大于0为向PES售电，小于0则为从PES买电)。

忽略设备损耗，工业用户主体的运行模型应满足的约束条件如下：

1)用户的电负荷功率平衡约束。

Le(t)=Le0(t)+Ptran(t)+Pcut(t)

(14)

式中：Le0(t)为用户的电负荷；Le(t)为经过需求响应后用户的实际电负荷。

2)用户的可削减电功率上下限约束。

-Pcut,max≤Pcut(t)≤0

(15)

式中：Pcut,max为系统允许的最大可削减负荷量。

3)用户的可调整电功率上下限约束。

(16)

式中：fs(t)为t时段系统允许调整的电负荷占总电负荷的比例。

4)与外电网的交易量非负性约束。

(17)

5)用户的电功率平衡约束。

Le(t)-Pb(t)+PS(t)+Pe,i(t)-PPV(t)≤0

(18)

式中：PPV(t)为t时段的光伏出力值。

2 多主体合作运行纳什谈判模型

目前，电力行业常用的合作博弈方法包括shaply分值法、Stackelberg博弈、纳什议价等，shaply分值法忽略参与者之间的相互作用，Stackelberg博弈中参与者行动有先后顺序，都不契合本文的研究。而纳什谈判理论可以帮助分布式决策者实现资源的公平分配和帕累托最优效益[22]。同时，对于有合作潜力但存在利益冲突的主体，纳什谈判可以有效地使各个主体进行相互协调。

2.1 纳什谈判的基本原理

本文假设园区共享储能电站和各个工业用户属于不同的利益主体，各主体都寻求达成交易共识，公平合理地确定电能交易功率和电价，以此最大程度地提高个体与整体的收益。一个标准的纳什谈判问题可表示为：

(19)

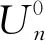
为了激励各主体之间的相互协调，纳什谈判的可行集只包括比谈判破裂点更好的收益。模型式(19)可以进一步等价地转化为：

(20)

2.2 基于纳什谈判的合作模型

将纳什谈判理论应用于本文园区共享储能电站和各工业用户主体之间的合作问题，可以得到如下基本模型：

(21)

模型式(21)本质上是非凸非线性优化问题，若将此模型进行等效变换，转化为系统收益最大化和电能交易支付谈判子问题，便会大大降低求解难度。

(22)

由式(4)、(13)可得Cpu+C′pu=0，则max(UPES+Ui)⟺max(ωi+ωp)。

子问题1：系统收益最大化问题。

(23)

子问题2：电能交易支付谈判问题。

(24)

由上述模型和分析可得，式(23)求解的是园区共享储能电站和工业用户主体总收益的最大值，但是求解过程中共享储能电站和工业用户之间的交互成本Cpu和C′pu相互抵消，因此就无法求解各主体单独的电能交易额，这也是引入纳什谈判理论的重要性。通过求解子问题2便可以求得电能交易价格，以此确定各主体的电能交易额。

3 多主体合作运行纳什谈判模型的求解

本文将采用交替方向乘子法，并在Matlab2016中调用商业求解器Cplex和优化求解器Mosek以及Yalmip工具箱对2个子问题进行分布式求解。

3.1 ADMM

ADMM既可以保护谈判时各主体的隐私，又具有处理速度快、收敛性能好等优点。ADMM主要用于求解带有约束条件的凸优化问题[23]：

(25)

式中：x、z为优化变量；A、B、c为相关矩阵。对应的增广拉格朗日函数可表示为：

L(x,z,λ)=f(x)+g(z)+λT(Ax+Bz-c)+

(26)

式中：λ为拉格朗日乘子；ρ为惩罚因子。

3.2 基于ADMM的系统收益最大化问题的求解

当满足Pe,i(t)+Qe,i(t)=0时，表明共享储能电站期望向工业用户销售的电量与工业用户期望向共享储能电站购买的电量一致，双方达成交易共识。为求解此问题，首先引入拉格朗日乘子λt、惩罚因子ρt和收敛精度ξ，则可以得到共享储能电站和工业用户主体的分布式优化运行模型。

1)共享储能电站分布式优化运行模型。

(27)

2)工业用户主体分布式优化运行模型。

(28)

然后根据分布式迭代模型，建立系统收益最大化问题的分布式算法，迭代公式为：

(29)

(30)

通过式(29)进行迭代，当满足式(30)的收敛条件时迭代停止，完成系统收益最大化问题的求解。

3.3 基于ADMM的电能交易支付谈判问题的求解

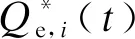
(31)

(32)

将式(31)、(32)代入模型式(24)，可得共享储能电站和工业用户主体的电能交易价格分布式优化模型。

1)共享储能电站电能交易价格分布式优化模型。

(33)

2)工业用户主体电能交易价格分布式优化模型。

(34)

然后根据分布式迭代模型，建立系统收益最大化问题的分布式算法，迭代公式为：

(35)

(36)

通过式(35)进行迭代，当满足式(36)的收敛条件时迭代停止，完成电能交易支付谈判问题的求解。ADMM算法流程如图2所示。

4 算例分析

4.1 算例系统

算例选取3家典型工业用户，用户1为食品制造厂，用户2为纺织服装制造厂，用户3为家具制造厂，其电负荷曲线和光伏出力曲线如图3所示。共享储能电站的最大和最小荷电状态分别取0.9和0.1，初始荷电状态为0.2，最大容量为500 kW·h。用户使用共享储能电站的最大充放电功率为185 kW。系统允许的最大可削减负荷量取总电负荷量的0.10，可调整负荷量取总电负荷量的0.15。上网电价取0.3元/(kW·h)，分时电价如表1所示。

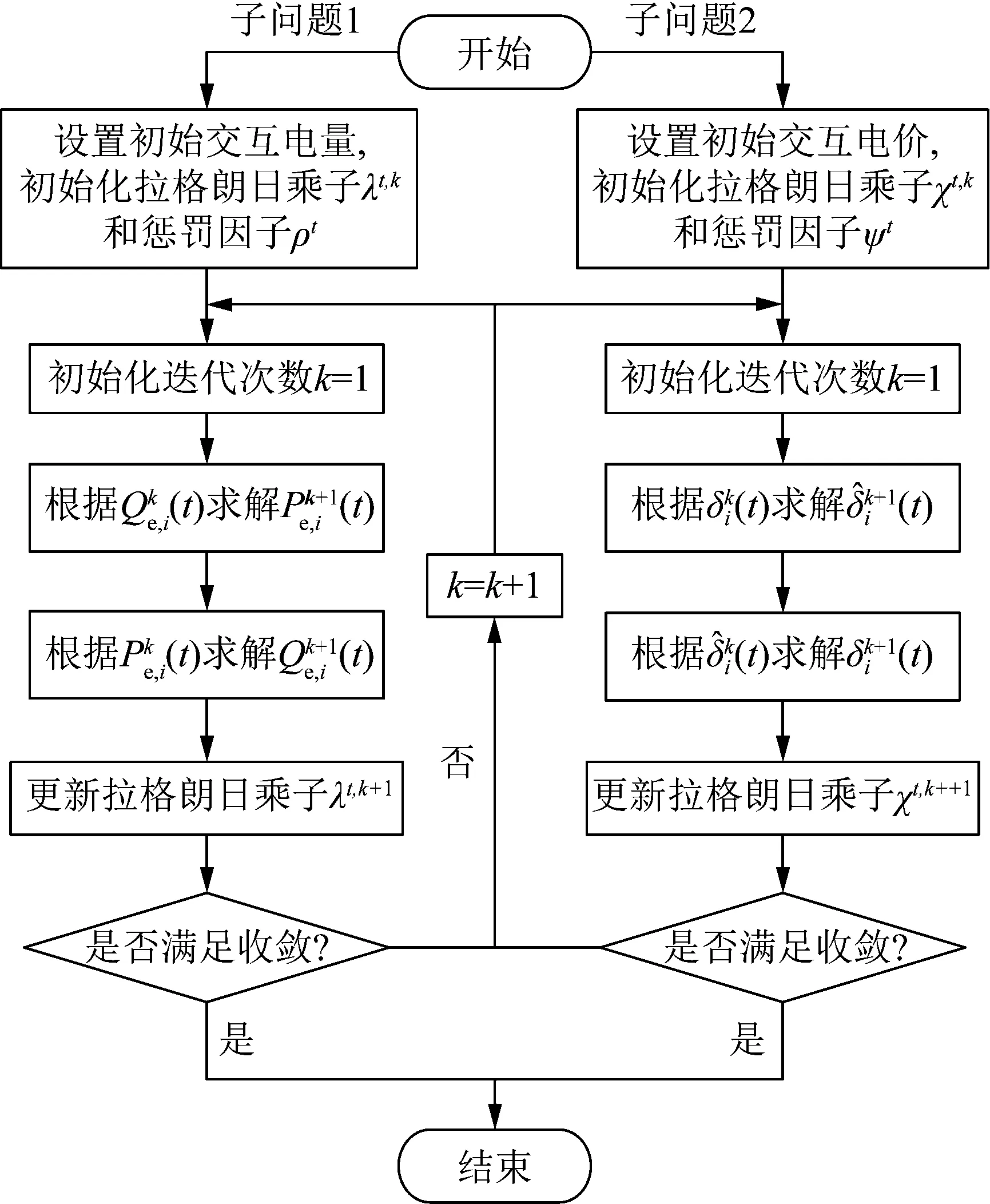
图2 ADMM算法求解流程Fig.2 Flow chart of ADMM algorithm solving

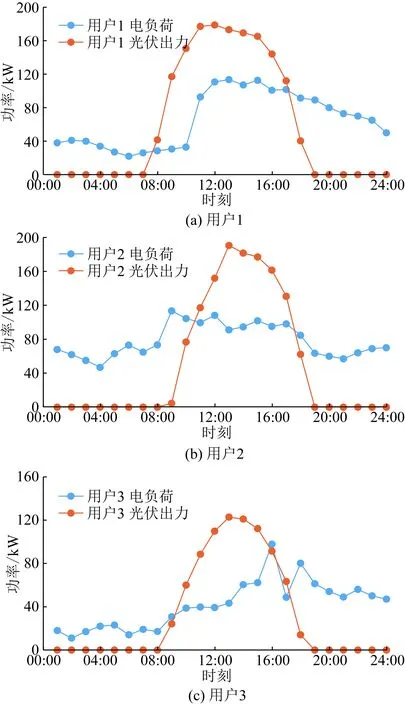
图3 用户电负荷和光伏出力曲线Fig.3 Curves of user electric load and photovoltaic output

表1 电价参数Table 1 Electricity price

4.2 仿真结果分析

4.2.1 各主体电能交易分析

共享储能电站和各用户主体间的交互电量如图4所示。各主体的电能交易结果如图5—7所示。共享储能电站的充放电功率和电量状态如图8所示。

图4 共享储能电站和用户的交互电量Fig.4 Interactive electricity between shared energy-storage power station and users

图5 用户1的电能交易结果Fig.5 Electricity transaction results of user 1

图6 用户2的电能交易结果Fig.6 Electricity transaction results of user 2

图7 用户3的电能交易结果Fig.7 Electricity transaction results of user 3

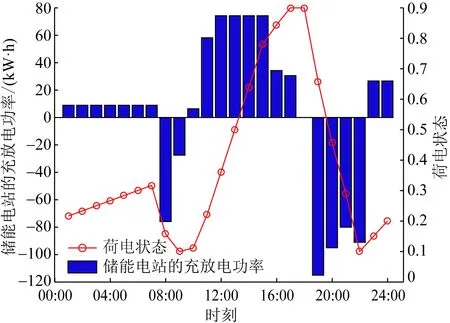
图8 共享储能电站的充放电功率和电量状态Fig.8 Charging/discharging power and electricity state of shared energy-storage power station

由图3(a)和图5可以看出，在时段00：00—07：00和17：00—24：00，由于光伏出力小于用户的电负荷功率，无法保证用户的用电需求，用户1通过共享储能电站放电和从外电网购电的方式来满足负荷需求。在时段07：00—17：00，光伏出力大于用户的负荷需求，在此阶段用户通过共享储能电站将剩余电能存储起来，避免了弃光现象的发生，又考虑到共享储能电站的最大充放电功率的因素，用户亦可将部分电能出售给外电网，保证自身的最大效益。此外由于时段18：00—22：00属于电网电价的峰时段，为了最大程度地降低运行成本，用户1利用共享储能电站的放电量较大，以此最小程度地从电网购电，在18：00—19：00时段使用共享储能电站放电达到最大功率56.3 kW。

由图3(b)和图6可以看出，在时段10：00—17：00，光伏出力大于用户的用电负荷，剩余的光伏出力通过共享储能电站存储在电站内部。在其他时段，用户通过向外电网购电和利用共享储能电站放电的方式来满足用电需求。尤其在时段07：00—09：00，其用电需求远大于光伏出力，此时段也并非电价谷时段，因此选择从共享储能电站放电，08：00—09：00时段的交互功率为全天最大，达到108.8 kW。

由图3(c)和图7并结合其他用户的电能交易结果可得，各用户的用电行为大体具有一致性，在电网电价谷时段大量购买电量，并将剩余电能存储在共享储能电站中，在峰时段会优先通过共享储能电站放电的方式来满足用电需求，从而降低运行成本。同时对于外电网而言，用户和共享储能电站的运行方式和购电计划可以缓解高峰期的供电压力，具有明显的削峰填谷效果。此外还可以看出，为了兼顾个体和整体的利益，用户、共享储能电站和外电网之间几乎每个时段都会保持电量的交互。

由图8可以看出，在时段22：00—07：00和09：00—17：00共享储能电站处于放电状态，其余时间为充电状态。在时段16：00—18：00，共享储能电站电量达到最大值0.9Emax(Emax为储能单元的最大容量)，在时段08：00—09:00和21：00—22：00，共享储能电站电量达到最小值0.1Emax。在时段11：00—15：00共享储能电站达到最大放电功率74.2 kW，在时段18：00—19：00共享储能电站达到最大充电功率115 kW。共享储能电站经过一个周期的运行，最后回到初始状态0.2Emax，以此保证下一个周期的正常运行。此外由图3—7还可以看出，用户的电负荷达到平衡状态，没有出现弃光现象，有利于新能源的消纳。

4.2.2 各主体运行效益分析

图9为共享储能电站与各工业用户主体之间的交易电价。为了体现本文交易模式的价格优势，假设各主体间的交易电价大于上网电价。

图9 各主体间的电能交易价格Fig.9 Electricity transaction price

表2—5分别给出了各主体合作前后的运行收益对比和运行成本对比。可以看出，一个周期内共享储能电站主体在纳什谈判合作后总收益提高了233.691 0元，3个用户主体的运行成本分别降低了261.141 7、251.598 2、151.002 5元，下降幅度分别为73.09%、45.30%、49.26%。这说明了共享储能电站和各用户主体通过纳什谈判合作都大幅提升了自身的效益，可见该方法兼顾了整体利益和个体利益，达到了预期的目标。

表2 共享储能电站合作前后运行收益对比Table 2 Comparison of operation income before and after cooperation of shared energy-storage power station 元

表3 用户1合作前后运行成本对比Table 3 Comparison of operation cost before and after user 1 cooperation 元

表4 用户2合作前后运行成本对比Table 4 Comparison of operation cost before and after user 2 cooperation 元

表5 用户3合作前后运行成本对比Table 5 Comparison of operation cost before and after user 3 cooperation 元

5 结 论

共享储能电站是随着共享经济的理念出现的新型储能运行方式，而纳什谈判理论属于合作博弈范畴，两者具有一致的核心理念，本文基于纳什谈判建立共享储能电站和工业用户的合作运行模式，并将此问题转化成系统收益最大化和电能交易支付谈判2个子问题进行分布式求解。通过算例分析，可得出以下结论：

1)利用交替方向乘子法求解系统收益最大化和电能交易支付谈判2个子问题具有较好的收敛性，而且此算法保护了各参与主体的隐私信息，同时也具有收敛速度快、精度较高的优点，完成了本文合作运行问题的高效求解。

2)通过各主体的交易结果分析，用户的电负荷达到平衡状态，减少弃光现象，有利于新能源的消纳。对电网而言，各主体的用电行为有利于缓解电网用电压力，具有明显的削峰填谷效果。

3)与合作前对比可得，共享储能电站和工业用户整体收益提升，而且各个主体的效益也都得到明显提升，同时兼顾了整体利益和个体利益。