基于改进遗传算法的铁路物流中心功能区布局优化研究

张 恒

(中国铁路武汉局集团有限公司 计划统计部，湖北 武汉 410073)

0 引言

近年来，随着货运需求的增加及市场竞争的加剧，铁路物流基地和货运场站作为铁路货运中心枢纽，是货运至关重要的环节，其规划和设计将影响整个铁路货运效率。针对铁路物流中心规划设计进行研究，对我国铁路货运适应现代物流的竞争环境并取得主导地位现实意义重大。由于货物品类不同，且铁路物流中心各功能区之间的货运量存在差异，功能区之间的相关性各有不同。另外，加上物流中心的客观限制条件，使得铁路物流中心功能区布局优化成为一个NP 难问题。

目前我国关于物流中心的研究多集中于物流中心运营模式理论[1]、单一物流中心选址[2]及传统货运站向现代物流中心转化的定性分析[3-4]等方面。求解铁路物流中心功能区布局问题的方法主要有数学模型法[5-6]、系统布置规划法(Systematic Layout Planning，SLP)[7]及计算机仿真等。近年来，从定性和定量2方面考虑的SLP 方法应用较多，采用的算法主要有启发式算法、智能算法、计算机仿真方法等，其中智能算法被广泛采用，包括遗传算法、模拟退火算法、蚁群算法等。针对铁路物流中心功能区布局优化模型，冯芬玲等[7]设计遗传算法进行求解，通过对中心点位置和摆放方式进行编码，将约束条件作为惩罚加入适应度函数；由于各功能区域相互位置的约束，造成该种方法无法保证解的可行性，容易产生不可行解；同时搜索空间过大，不易搜索到优解。谷乐阳[8]采用严格分层布局的方式进行求解，保证解的可行性，然而这种方法大大缩小了解的搜索空间，存在忽略相对优解的情况。

通过对铁路物流中心功能区布局优化模型求解算法研究，提出一种高效遗传算法。采用改进分层思想，通过从左到右、从下往上的紧密堆积布局方式，同时对各功能区域竖直采用连续上下位移选择，优化物流区域布局。对编码方式进行改进，针对功能区域布局顺序、堆积方式和摆放方式，分别采用自然整数编码、离散二进制编码和连续区间的二进制编码方式进行编码，并进行遗传操作，搜索区域布局优化解。通过算例比较，体现了改进遗传算法的优越性。算法在保证解可行的前提下，扩大了搜索范围，提高解质量，从而能够获得更优的铁路物流中心功能区布局方案，为铁路物流中心功能区布局提供技术支撑。

1 铁路物流中心功能区布局优化模型

铁路物流中心主要通过铁路联络线以铁路运输方式进行物流活动，包括货物承运、配送、储存、运输和交付等，按其作业流程及各项作业特点划分为基本功能、增长功能和辅助功能3 大类12 个功能区。基本功能区包括：理货区、流通加工区、仓储区。增长功能区包括：交易展示区、卡车停车场和办公服务区。辅助功能区包括：后勤保障区、生活服务区、绿化区，以及物流中心储备用地和道路规划用地等功能区。

一般将物流区域假设成平面图，物流中心规划区域和功能区域形状为矩形。功能区域的集合为N，且n=[N]为功能区域的数量。假设功能区域的边分别与物流中心规划区域坐标图的X 轴和Y 轴平行，且每个功能区域在进行布局时有横倒和竖立2 种放置方式，对于功能区i，si=1 表示横倒，si=0 表示竖立。功能区域放置方式的向量形式为S=(si)n×1，设功能区域i的中心位置坐标di为(xi，yi)，功能区域的中心位置坐标向量表示为d=(di)n×1，则以(d，S)为决策变量的铁路物流中心功能区布局优化模型如下。

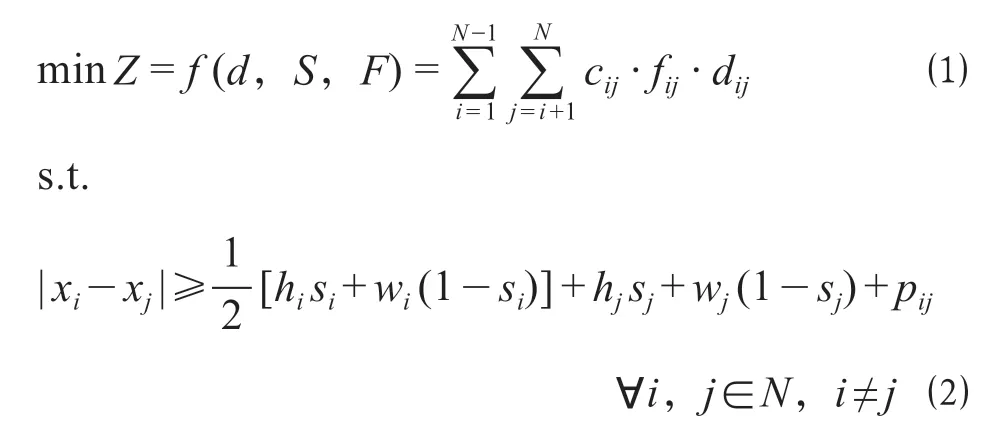
式中：Z为总成本，元；F为fij的向量，F=(fij)n×n，其中，fij为功能区域i与区域j日均物流量，t；cij为单位物流量单位距离的成本，元/ t·m；dij为曼哈顿距离，即dij=|xi-xj|+|yi-yj|，m；hi和hj分别为功能区i和区域j的水平边长度，m；wi和wj分别为功能区域i和区域j的垂直边长度，m；pij为功能区边界之间的最小间距，m；H和W分别为物流中心规划区域水平边和垂直边的长度，m。

对于一般物流区域布局优化包括2 个约束条件。①不重叠约束。两相邻功能区域不得相互重叠，如公式⑵—公式⑶。②功能区边界约束。各功能区的边界不得超出物流中心规划区域，如公式⑷—公式⑸。需要注意的是，针对具体的物流区域布局问题，还需增加相应的约束，比如铁路物流中心功能区布局中存在铁路装卸线功能区固定约束、物流中心出入口约束等。铁路物流中心功能区布局优化模型为非线性混合整数规划模型，难以用凸规划算法直接求解，属于NP 难问题，适宜采用遗传算法进行求解。

2 改进遗传算法设计

2.1 分层布局方式改进

遗传算法的编码方式对遗传操作方式及适应度函数均有直接影响，同时也影响算法对于解的搜索能力，包括算法整体计算量和搜索解的质量。对于铁路物流中心功能区布局优化模型，决策变量为(d，S)，即各功能区域的坐标和放置方式。其中功能区域放置方式可以采用二进制编码表示。而对于各功能区域坐标，如果直接对其进行编码，虽然搜索范围包含了所有解空间，但存在2 个缺点：一是基于一定的精度，对实数区间进行编码，编码长度较长，且随着精度提高，编码长度也相应增加；二是由于直接对坐标编码，编码并没有考虑约束条件，则大部分解的编码无效或不正确，且进行遗传操作时，获得的解也会包含大量无效解。

设计采用分层思想解决上述问题，分层布局方式主要是针对功能区的整体布局。将规划区域进行分层，并采用从左到右、从下往上的紧密排列方式对功能区域进行布局，利用自然整数编码对功能区域布局顺序进行编码，即定义一个功能区域与布局顺序一一对应的函数o :N→{1，2，3，…，|N|}。分层思想示意图如图1 所示，对7 个功能区域，按照顺序从左到右、从下往上分层排列，同时同层紧密排列。由于第1 层容不下功能区域5，所以功能区域5 只能布局在第2 层。采取这种方式布局后记录各功能区域坐标，获得该编码下的布局解。按照这种方式编码后，每一组编码均会获得一个解，且通过这种方式获得的解的可行度大大增加。

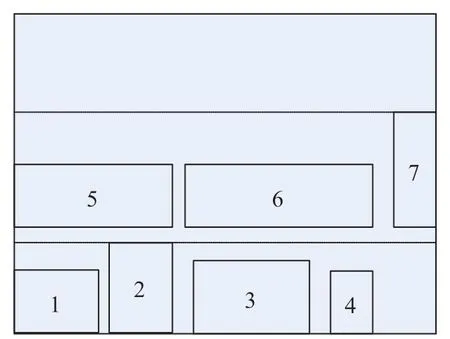
图1 分层思想示意图Fig.1 Hierarchical thinking

尽管图1 所示分层布局方式提高了解的质量，同时也大大削弱了解的搜索能力和搜索范围。为了同时提高算法搜索解的效率和质量，采用改进的分层思想，按照从左到右、从下往上的紧密堆积方式进行布局，并采用三进制对堆积方式进行编码。改进分层思想示意图如图2 所示。图2 中，3 个子图分别表示功能区域7 的3 种堆积方式。

在图2 的布局方式中，第1 层包括功能区域1～ 4，第2 层包括功能区域5～ 7。对于功能区域7，方式1 是将功能区域7 布局在该区域X 轴范围内所能放置的最下面；方式2 是将功能区域7 布局在该区域X 轴范围内最高的水平高度，与该区域X 轴范围之外的左边紧挨的第1 个区域水平高度上进行堆积，即在区域4 的水平高度上堆积；方式3 是将功能区域7 布局在第1 层所有功能区域中最高的水平高度基础上，即在区域2 的水平高度上堆积。

图2 所示的布局方式，从左到右紧挨着布局，会出现某功能区域无法容纳的情况，即超出规划区域Y 轴边界。对于这种情况，越界处理方法如图3 所示。第1 层包含区域1～ 4；第2 层包含区域5～ 7；第3层包含区域8 和区域9；当布局到区域10，且采用堆积方式3，在堆积第4 层时，由于区域10 从最左边开始布局，剩余竖直高度不够，造成Y 轴越界，此时找出区域10 的X 轴覆盖区域中水平高度最高的区域，即区域8，移动区域10 的X 轴，使其布局在区域8 的右边，重新布局。此时第4 层可以包含区域8。由于采用堆积方式3，则若Y 轴高度不够，可以降低区域10，使其刚好能布局到规划区域内为止，此时第4 层包含区域8 和区域10。如果此时仍越界，重复上述过程，直至将区域10 布局到规划区域内为止，同时记录各层区域信息。

图2 改进分层思想示意图Fig.2 Improved hierarchical thinking

图3 越界处理方法Fig.3 Cross-border handling method

通过改进分层的布局方法，扩大了原来分层布局方法下搜索解的范围，同时保持了搜索质量，提高了物流区域布局优化解的搜索效率。

2.2 堆积方式改进

为了进一步扩大解的搜索范围，对堆积方式进一步改进。改进的堆积方式，主要针对单个功能区域的纵向堆积。当对区域i进行堆积时，找出区域i的X 轴覆盖的所有区域中的最低水平高度yˆi为下限，同时找出前一层中所有区域的最高水平高度yˇi为上限，此时能够通过参数ri(0 ≤ri≤1)，确定区域i的Y 轴坐标yi如公式 ⑹ 所示。

式中：ri表示第i个区域的堆积参数。

同样以图2 中区域7 的布局堆积方式为例，区域高度的随机确定方法如图4 所示。水平高度上限为d，水平高度下限为0，则确定r7=0.5，则区域7的Y 轴坐标为：r7=0.5d+0.5h7。

图4 区域高度的随机确定方法Fig.4 Random determination of area height

对堆积方式的编码等价于对各区域的堆积参数ri进行编码，由于任何区域的堆积参数的范围均为[0，1]的连续区间，则可以利用连续区间的二进制编码近似表示。

综上，通过引入堆积参数确定堆积方式，以及相应的编码方式，进一步扩大了解的搜索空间，同时保持了分层思想的优点，可实现提高搜索解的质量。

2.3 遗传算子与算法流程设计

采用符号编码和二进制编码相结合的方式表示布局问题的解空间。采用二进制编码{0，1}表示功能区域的放置方式，“0”代表横放，“1”代表竖放；采用自然数编码{1，…，N}表示功能区编号，特别将功能区域12 与功能区域10 交换位置，方便更好地求解问题。此外，以[0，1]之间的随机数对堆积方式进行编码。每条染色体代表1 种布局方案，用C={Z1，Z2，…，ZN|T1，T2，…，TN|R}表示，其中Zi(1 ≤i≤N)代表功能区域编号；Tj(1 ≤j≤N)代表与之对应的功能区域放置方向；R表示堆积方式。

以目标函数即布局方案的成本函数为适应度函数，对个体的编码串进行解码处理，从而得到个体的表现型，由个体的表现型计算出目标函数值。淘汰不满足要求的染色体，而对于满足限制条件的个体，以轮盘赌法作为选择算子。具体操作过程为：对满足要求的个体进行分类处理，适应度高的个体不需要参与遗传操作直接进入下一代种群中，以保留优秀的基因，其他个体则采用轮盘赌法从上一代选择n-1 个个体进行接下来的遗传操作，使得下一代的种群规模保持不变。对选择出的个体进行交叉操作，为保证交叉操作的有效性，避免子代无变化情况，采用部分交叉操作方式，即随机选择2 个个体，选择交叉概率下的部分染色体编码进行交叉映射操作。在进行变异操作时，设计2 种变异方法以增加种群的多样性，包括基本位变异和交换变异。基本位变异是指对随机个体的随机位置产生随机编码替代的变异方式；交换变异是指对一条染色体的2 个部分进行交换操作，以获得新的子代的方式。遗传算法流程图如图5 所示。

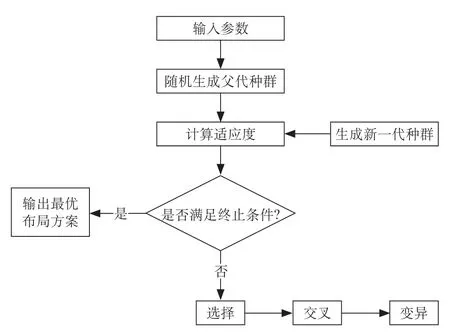
图5 遗传算法流程图Fig.5 Flow chart of genetic algorithm

3 算法验证

采用冯芬玲等[7]研究的算例，设置种群个数为500，最大繁衍代数为100，交叉概率为0.9，变异概率为0.01。分别对简单堆积方式和改进堆积方式进行求解，从而验证基于分层思想的改进堆积方式的优化效果。

对分层思想下的简单堆积方式进行求解，简单堆积方式的物流区域布局如图6 所示。由图6 可知，各功能区域均满足不重叠约束、功能区域边界约束、固定约束和物流中心出入口约束。功能区简单地根据下一层的最高点的纵坐标和各个功能区之间的最短间距约束进行堆积。分层思想下的算法收敛图如图7所示。由图7 可知，遗传算法收敛速度很快，通过14 代计算，目标函数值快速下降，最后经过100 代遗传，目标函数值达到6.673 9 万元。该种方式下，最优染色体为C1={3，11，4，9，6，7，10，8，2，1，5 | 0，0，0，0，0，0，1，1，0，0，0}。由于功能区10 为固定的坐标和放置方向，因此，染色体只考虑了其余11 个功能区，即包含11 个因子。

图6 简单堆积方式的物流区域布局图Fig.6 Layout of logistics area with simple accumulation method

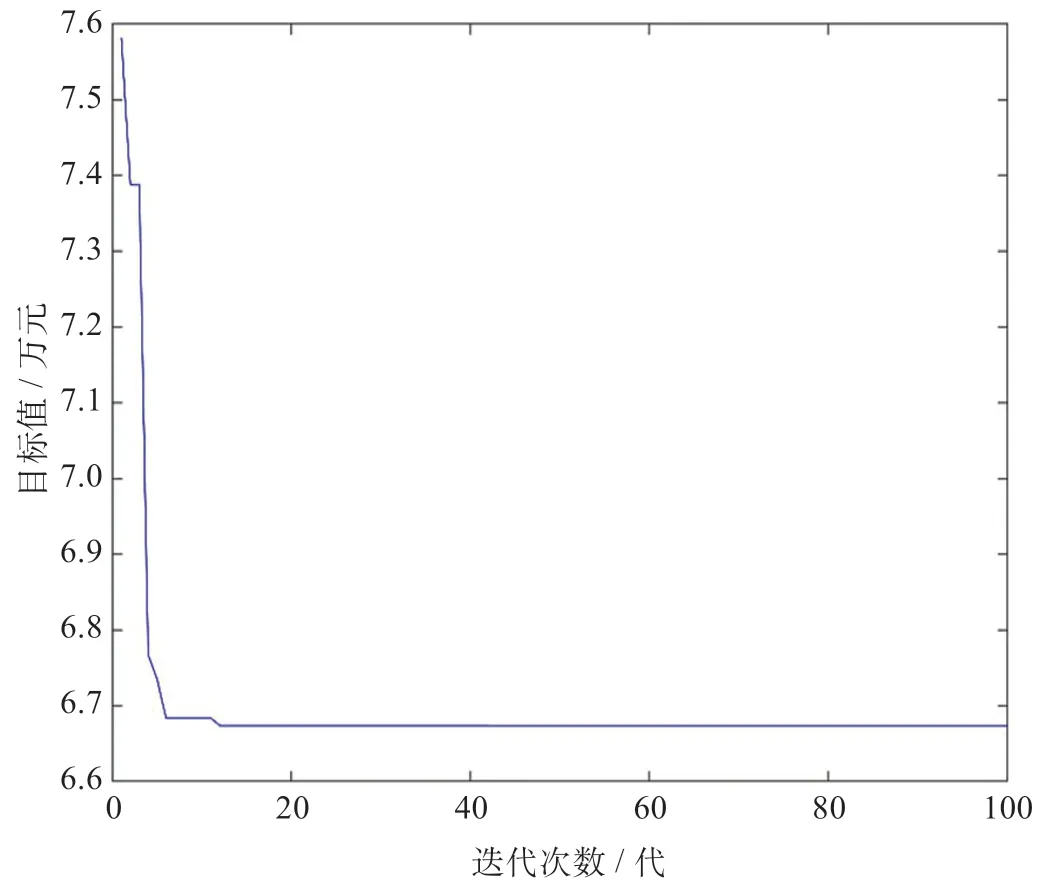
图7 简单堆积方式的算法收敛图Fig.7 Algorithm convergence graph of simple accumulation method

对分层思想下的改进堆积方式算例进行求解，改进堆积方式的物流区域布局图如图8 所示。各功能区之间位置更加紧凑，布局更加紧密，得到较为满意的布局结果。改进堆积方式的算法收敛图如图9所示，由图9 可知，遗传算法收敛速度很快，通过16 代计算，目标函数值快速下降，最后通过100 代遗传，目标函数值达到5.887 2 万元，相比简单堆积方式的情况，目标值下降了约11.79%。在此方案下，最优染色体为C2={7，3，5，10，4，2，11，6，1，9，8 | 1，1，1，1，0，0，0，0，0，1，0 | 0.750 79}，由此验证，通过对堆积方式改进，能够获得更加优化的目标函数值。

图8 改进堆积方式的物流区域布局图Fig.8 Optimized logistics area layout map with improved accumulation method

图9 改进堆积方式的算法收敛图Fig.9 Algorithm convergence graph with improved accumulation method

通过计算，2 种方式的最优方案功能区坐标如表1 所示。除了部分特殊功能区的位置较为相似，其他功能区的分布情况截然不同，同时可以看出改进堆积方式的遗传算法所求解更优。

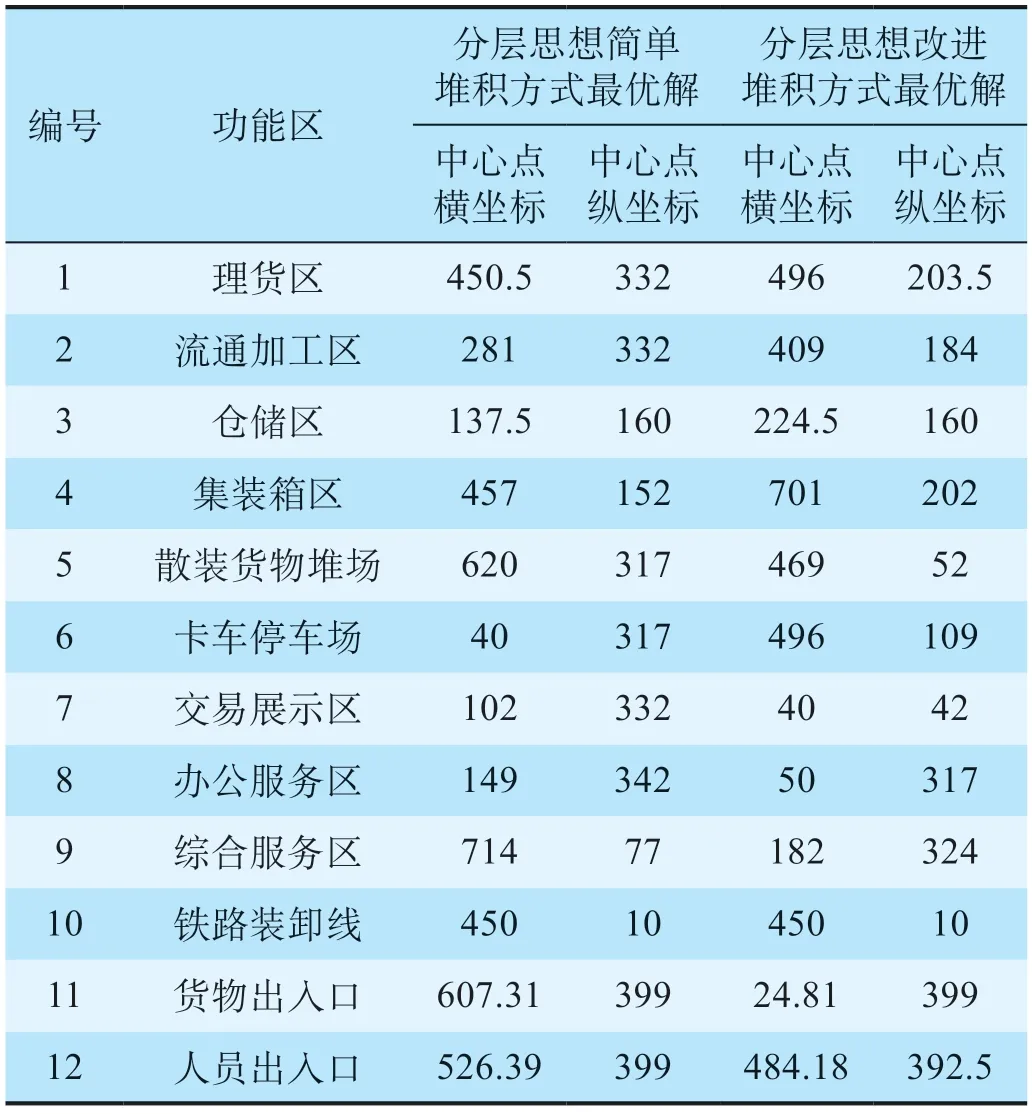
表1 2种方式的最优方案功能区坐标 mTab.1 Coordinates of the optimal functional area schemes for the two methods

4 结束语

针对求解物流区域布局优化模型，通过改进分层布局方式和堆积方式，设计不同编码方案，对提高算法搜索解质量，扩大算法搜索解空间具有良好的效果。通过改进前后的遗传算法对算例求解，表明所改进遗传算法在短时间内获得更加满意的结果，目标值较改进前计算目标值优化11.79%，验证了改进后的布局方法可以有效降低各功能区之间的物流成本。此外，设计的算法能够提高整个物流中心的运行效率，从而在竞争日益激烈的物流运输中，提高铁路的竞争力。算法基于紧凑型分层思想设计，但是对区域互斥情形考虑不全面，为了继续扩大搜索解的空间，同时保证解的可行性，可以对每层高度作为决策变量进行进一步优化。