黄河下游引黄灌区水资源优化配置研究
刘 昀,李 倩,王 静
(黄河水利委员会山东水文水资源局,济南 250100)
1 动态规划的基本原理
动态规划,缩写为DP,是20世纪50年代初期由美国数学家贝尔曼等人提出, 并逐渐发展起来的数学分支, 是一种多阶段决策过程最优化问题的数学规划方法。用动态规划法求解的问题,必须具备以下特点:①满足最优化原理;②所研究的系统能划分成若干阶段;每个阶段都能作出决策;③相邻两个阶段的状态能够转移并且这种转移是通过使用某一决策而实现的[1]。
1.1 基本概念
1.1.1 阶段
阶段可定义为所研究的事物在发展中所处的时段或步骤(或某一局部空间),以序列数字k=1,2,…,K表示。
1.1.2 状态
描述系统演变过程中各阶段所处状况的特征量称为状态,常以符号S表示。描述过程状态(或系统状态)的变量,称为状态变量。它可以是一维变量,也可以是多维变量。 在任一阶段k可有若干个状态,构成该阶段的状态集合Sk。

式中 r为阶段k的状态点数。
1.1.3 决策
某阶段状态给定后, 从该状态演变到下一阶段某个状态的选择称为决策,用d表示。 在多阶段决策过程的任一阶段中,当阶段的状态Sk给定后,如果做出某一决策dk, 则阶段初的状态就转移到一个相应的下一阶段状态Sk+1,描述决策的变量称为决策变量。
1.1.4 策略
由第一阶段开始直到终点为止的过程称为问题的全过程。 Dk是由每个阶段的决策Dk(k=1,2,…,K)所组成的决策序列,称为全过程策略,简称策略。
1.1.5 状态转移方程
状态转移方程, 即从过程的一个状态转移到另一个阶段某状态的演变过程,Sk+1=Dk(Sk)表明第k+1阶段的状态变量的值随第k个阶段的决策变量Dk和状态变量Sk确定。
1.1.6 指标函数
指标函数是描述过程优劣的数值指标,如式(1):

1.2 动态规划数学模型的解法
动态规划的数学模型主要包括: 系统的阶段变量、状态变量、决策变量、目标函数、约束条件等。 数学模型的解法一般分为逆序解法和顺序解法。 逆序解法是从终点向前推移, 使每一阶段到最后都能达到最优,最后求得整个过程的最优解。顺序解法是从起点开始,使起点到每一阶段都能达到最优,最后给定全局最优解。
2 典型灌区水资源优化配置
2.1 灌区概况
选取黄河下游陈垓灌区作为模型计算的典型灌区,陈垓灌区位于山东省济宁市梁山县境内,始建于1959年, 有效灌溉面积3.68万hm2, 主要农作物为小麦、玉米、棉花,小麦和玉米种植面均为2.45万hm2、棉花种植面积0.36万hm2,复种指数为1.43。 灌溉水利用系数为0.56。
2.2 灌区典型年作物灌溉水量
根据该灌区历年降水量及气象数据可以计算出不同降雨频率情况下充分灌溉时作物的需水量,经计算该灌区降雨频率为50%时(平水年),小麦灌溉净水量2475m3/hm2,玉米灌溉净水量450m3/hm2,棉花灌溉净水量2475m3/hm2; 降雨频率为75%时 (干旱年), 小麦灌溉净水量2925m3/hm2, 玉米灌溉净水量675m3/hm2,棉花灌溉净水量2925m3/hm2。 这里净水量是指作物正常生长所需灌溉的水量,不包括蒸发、渗漏等损失水量[3]。
根据各作物的净灌水量可以算出降雨频率为50%时,充分灌溉条件下,灌区作物总需水量8066万m3,降雨频率为75%时,灌区作物总需水量9883万m3,水利部门分配给该灌区农灌用水许可水量7820万m3,根据其灌溉水利用系数, 计算出进入田间的净水量约4380万m3,远小于作物充分灌溉条件下的需水量。
2.3 水分生产函数及产生的效益
2.3.1 水分生产函数
作物水分生产函数, 是指在作物生长发育过程中, 作物产量与投入水量或作物消耗水量之间的数量关系。 作物水分生产函数可以确定作物在不同时期遇到不同程度的缺水时对产量带来的影响。
为了进行水资源优化分配, 达到最大效益的目的, 首先必须建立各种作物全生育期耗水量与产量的关系。 作物水分生产函数的特征曲线一般包括递增和递减两部分。当水分成为产量的限制性因素时,表现为递增函数; 水分成为产量的非限制性因素或过量实施造成减产时,表现为递减函数[4]。 因此,全生育期水分生产函数的数学模型多为抛物线型,全生育期水分生产函数的数学模型表达式,如式(3)。

式中 F(Qk)为作物产量(kg/hm2);Qk为灌水量(m3/hm2);a,b,c为经验系数。
参考林磊[5]对引黄灌区各作物建立的水分生产函数,各系数如表1。

表1 作物全生育期水分生产函数经验系数
各作物全生育期水分生产函数如图1~图3。

图1 小麦全生育期水分生产函数

图2 玉米全生育期水分生产函数
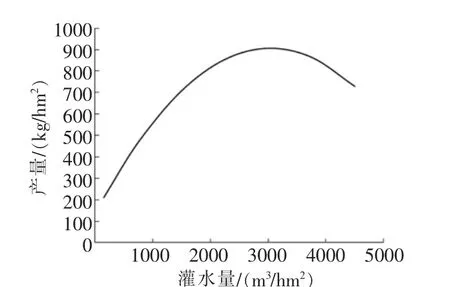
图3 棉花全生育期水分生产函数
2.3.2 作物经济效益
根据各作物的产量、 种植面积及目前的价格可算出各作物的经济效益, 各作物的价格根据黄河下游山东地区2021年粮食行情报价的平均值,小麦3.2元/kg,玉米2.8元/kg,皮棉24元/kg。
2.4 典型灌区水资源优化配置模型
针对陈垓灌区的情况, 采用动态规划的逆序解法建立数学模型。
2.4.1 阶段变量每一种作物为一个用水单位,可看作一个阶段,共3个阶段,阶段变量k=1,2,3。
2.4.2 状态变量和决策变量
状态变量为各阶段可用于分配的有效水量,即从第3种作物到第K种作物分配的水量,以qk表示;决策变量为分配给第k种作物的水量,以xk表示。
2.4.3 目标函数
设fK(qK)为以总水量Q分配给3种作物而获得的最大总净效益。计算净效益时根据水分生产函数、各作物的种植面积及价格,则目标函数如式(4)。
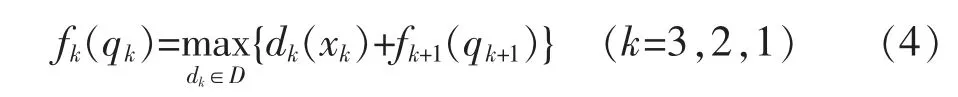
2.4.4 约束条件
(1)供给各种作物水量之和不超过水资源总量Q:

(2)供给第k种作物的水量xk不超过在第k阶段可用于分配的有效水量Q-qk+1:

动态规划就是要在系统的阶段变量、状态变量、决策变量、约束条件、边界条件约束下,寻求目标函数最优值和相应的最优决策序列。 各种作物分得的水量可以通过优化程序来获得, 本程序分为3个阶段, 需要先将状态变量、 决策变量在可行域内离散化, 离散间隔即步长为10, 然后由最后一个阶段开始,逆序进行逐阶段择优计算,最后输出计算结果。
计算程序的流程如图4:

图4 模型计算流程
根据作物灌溉可引黄水量及灌溉水利用系数,输入净水量4380万m3,输入小麦、玉米、棉花的种植面积,最终计算出灌区最大净效益为6.285亿元,小麦灌溉净水量为2010万m3,玉米灌溉净水量为1750万m3,棉花灌溉净水量为630万m3, 分别占总水量的46%,40%,14%。基于以上计算结果,灌区可以根据当年的实际情况按作物不同生育期需水比例引用黄河水进行灌溉,从而使灌区获得最大的经济效益。
3 结语
模型的建立为黄河水资源优化配置提供了决策依据,从而使有限的水资源得到有效合理的利用。 今后模型的建立还可从不同作物种植面积和水量两者优化进行考虑, 可利用模型调整不同作物种植面积及不同作物分配水量, 从而使有限的水资源发挥最大的经济效益。

