基于XFEM 的管道表面裂纹环向扩展数值模拟

陈 飞， 丁 宁， 王馨怡， 张 帆， 刘艳军

(1. 中石化川气东送天然气管道有限公司， 湖北 武汉 430070；2. 西南石油大学石油与天然气工程学院， 四川 成都 610500)

0 前 言

近年来由于能源需求日益增长，敷设管道的数量也与日俱增[1]。 据统计，我国管道出现事故的原因包括管材与焊缝缺陷等__[2]。 由于现场焊接质量控制难度大、排查整改难度大等原因，导致管道在运行过程中容易发生开裂，引起管道泄漏甚至断裂。

有限元方法(Finite Element Analysis， FEA)可以精确地模拟管道中的裂纹扩展[3]，但每次扩展后均需要重新划分网格以匹配裂纹几何形状，因此被认为是过于复杂的裂纹扩展建模方法。 1999 年，Belytschko 等[4]提出了扩展有限元法(Extended Finite Element Method，XFEM)用于解决裂纹扩展问题。 紧接着Moës 等[5]引入阶跃函数和裂尖函数2 种扩充形函数分别描述裂纹面和裂尖；随后Sukumar 等[6]又将XFEM 的使用由二维扩展到三维；Daux 等[7]利用XFEM 对裂纹分叉成功进行了模拟；Fries 等[8]通过局部网格细化和悬点进行扩展有限元分析从而解决了裂尖不连续的问题；Belytschko等[9]对XFEM 的任意不连续性进行了描述；Sukumar等[10]运用XFEM 来模拟含孔洞等不连续问题；Rethore等[11]通过XFEM 建立了动态裂纹扩展的模型，并验证了数值算法在线性条件下计算的稳定性；Pourmodheji等[12]将XFEM 用于解决延性裂纹扩展问题；Singh 等[13]将XFEM 用于解决疲劳裂纹扩展问题；Afshar 等[14]利用XFEM 解决复合材料断裂问题；Shen 等[15]将XFEM 用于不可压缩材料的断裂问题。 该方法克服了传统有限元网格划分困难等问题，因其无需对齐网格、裂纹扩展不需重新进行网格划分、网格较稀疏也可以得到精确度高的解等原因，成为目前进行模拟裂纹扩展的主流方法。

本工作基于 XFEM 方法， 运用有限元软件ABAQUS，针对含表面裂纹的管道在一定内压及拉伸力的作用下的裂纹扩展规律进行数值模拟研究，并探讨了裂纹初始大小、位置以及不同内压对管道内外表面裂纹的环向扩展的影响，为不同情况下含不同种类裂纹的管道的运营及维护提供科学的指导意见，在保障安全的前提下，充分发挥管道材料的潜能，减少不必要的经济损耗。

1 基本理论

XFEM 的核心思想是用带有不连续性质形函数基的扩充函数来处理计算域内的间断情况，且不连续场的描述完全独立于网格边界[16]。 扩充函数一般需要包含裂纹尖端处的奇异性和裂纹表面表示位置跳跃的不连续函数。 基于单位分解扩充的近似位移矢量函数u可以表示为:

式中i—— 第i个节点，一共有n个节点

Ni(x)—— 有限元的节点形函数

ui—— 有限元连续部分解的节点位移矢量

H(x) —— 裂纹表面和Ui相关的不连续跳跃函数

Ui—— 裂纹表面节点扩充自由度矢量

Fλ(x)—— 裂纹尖端和Vi相关的弹性渐进函数

Vi—— 裂纹尖端处的节点扩充自由度矢量

λ—— 不同的次数

应用ABAQUS 软件中扩展有限元进行模拟时，适用的破坏起始判据是最大主应力(Maxps)或最大主应变(Maxpe)法则，本工作选择最大主位移法则(即在相同管道长度下管道起裂时的轴向位移)作为判断新裂纹萌生的依据。 当断裂指标f在一定误差ftol下达到1.0时，裂纹开始萌生[16]:

其中，断裂指标f可表示为:

2 计算模型

选择国内某长输管道及其沿线某站场管道进行模拟，该管线设计压力为10 MPa，运行压力为8 MPa，管道规格分别为φ273.0 mm×9.5 mm(站内)及φ508.0 mm×6.4 mm(长输)，通过ABAQUS 建立含裂纹的管道，假设管道焊缝与管道为等强度匹配，因此不特别建立含焊缝的模型。 由于管道对称，建立有限元模型时取管道的1/2 模型，计算模型长度取3D 左右，根据工程实际结合SENT 实验[17]，选用Ramberg-Osgood 本构模型，取材料为X60 钢，材料参数如表1 所示。

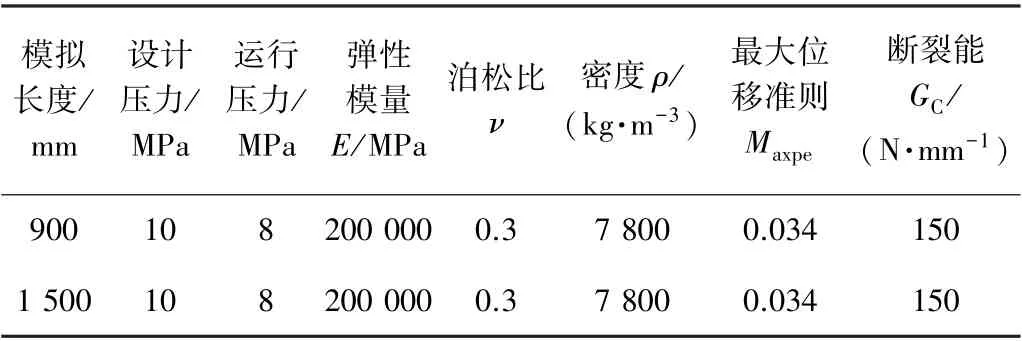
表1 材料参数Table 1 Material parameters

裂纹位于管道内侧或外侧，根据GB/T 19624-2019“在用含缺陷压力容器安全评定”[18]，以管道规格为φ508.0 mm×6.4 mm 的含内表面环向裂纹模型为例，截面图如图1 所示，图1 中a为裂纹缺陷的深度即半短轴长，B为管道的壁厚，c为裂纹的半长轴长，R为管道的外半径，Ri为管道的内半径，单位均为mm；装配图如图2 所示。 根据站场射线检测出的裂纹缺陷大小统计结果，大多射线检测出裂纹长度为4 mm 左右，故取圆形裂纹缺陷2a＝4 mm 即a＝2 mm。 根据管道的运行内压为8 MPa，设置第1 个分析步施加内压8 MPa；根据设置最大主应变法则作为裂纹萌生的判据，因此第二个分析步在管道两端各施加20 mm 均匀增大的拉伸位移载荷。

图1 管道内表面裂纹规则化示意图Fig. 1 Schematic diagram of regularization of cracks on the inner surface of a pipeline

图2 含圆形内表面裂纹管道装配图Fig. 2 Assembly drawing of pipe with circular inner surface crack

在ABAQUS 软件中，为保证模拟的精确度，避免由于网格划分过大引起的裂纹扩展路径方向以及扩展时间的误差，需对管道裂纹附近进行网格细化，网格细化后的管道如图3 所示。 采用牵引分离损伤法(damage for traction separation laws) 的最大主位移断裂准则(Maxpedamage)进行模拟[19]，为提高模型收敛性，将黏性系数(damage evolution)设置为1e-05(即1.0×10-5，下同，不再赘述)。 除此外设置PHILSM、PSILSM 以及STATUSXFEM[20]来观察管道环向裂纹的扩展情况。

图3 网格细化后的管道模型Fig. 3 Pipeline model after mesh refinement

3 管道表面裂纹扩展影响因素分析

将管道表面裂纹扩展分为内表面裂纹与外表面裂纹进行分析，根据GB/T 19624-2019“在用含缺陷压力容器安全评定”[18]，在本工作中取表面裂纹大小到a＜0.5B，因此分析裂纹大小变化对裂纹扩展的影响时，在规格为φ273.0 mm×9.5 mm 的管道中，模拟缺陷大小的范围在0.5～4.5 mm，在规格为φ508.0 mm×6.4 mm的管道中，模拟缺陷大小的范围在0.5～3.0 mm。 分析内压变化对裂纹扩展的影响时，内压范围为6～10 MPa。 此外，由于在规格为φ273.0 mm×9.5 mm 及φ508.0 mm×6.4 mm 的管道中表面裂纹扩展方向的规律相同，φ508.0 mm×6.4 mm 管道壁厚较薄，云图显示更明显，因此下列均以φ508.0 mm×6.4 mm 管道表面裂纹的裂纹水平集云图为例描述裂纹扩展方向。

3.1 圆形内表面裂纹扩展影响因素分析

3.1.1 裂纹大小变化对裂纹扩展的影响

在规格为φ508.0 mm×6.4 mm 的管道中，当a＝0.5 mm 时，经模拟得出，内壁裂纹先向管道环向方向扩展，再进行壁厚方向扩展直至穿透，裂纹面水平集函数(此函数描述裂缝面的位移，指定唯一函数用于描述裂纹面，即裂纹面上，距离裂缝的等高线，其值有正有负)云图如图4 所示，为保证观测裂纹扩展的准确性，选择裂纹面的PHILSM 图进行观察，其中PSILSM＝1.0×10-6代表完全开裂；对应最大Mises 应力云图见图5。 由图5可知，管道所受最大应力处于裂纹尖端位置，对应应力为604.6 MPa，而后突然减小至592.3 MPa。

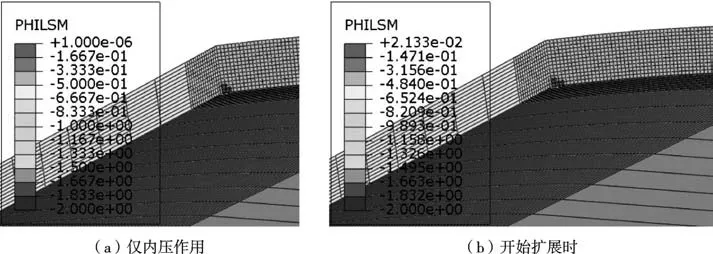
图4 管道裂纹面水平集函数云图Fig. 4 Cloud diagram of PHILSM of pipe crack surface

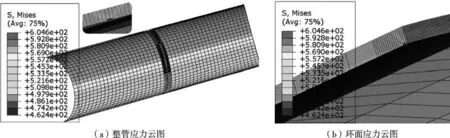
图5 启裂时管道对应最大Mises 应力云图(单位:MPa)Fig. 5 The maximum Mises stress cloud diagram corresponding to the pipeline when the crack was initiated

在规格为φ508.0 mm×6.4 mm 的管道中，当a＝3.0 mm 时，经模拟得出，内壁裂纹同样先向管道环向方向扩展，再进行壁厚方向扩展直至穿透，裂纹面水平集函数云图如图6 所示，对应最大Mises 应力云图如图7。由图7 可知，管道所受最大应力处于裂纹尖端位置，对应应力为596.9 MPa，而后突然减小至585.7 MPa。

图6 管道裂纹面水平集函数云图Fig. 6 Cloud diagram of PHILSM of pipe crack surface

图7 启裂时管道对应最大Mises 应力云图(单位:MPa)Fig. 7 The maximum Mises stress cloud diagram corresponding to the pipeline when the crack was initiated

根据GB/T 19624-2019“在用含缺陷压力容器安全评定”[14]，在均匀增大的拉伸位移为20 mm 时，运用ABAQUS 有限元模拟出在管道所受内压为8 MPa 时，含裂纹缺陷管道所受最大应力情况，裂纹启裂及穿透时管道轴向位移结果如表2。 由表2 可知，仅在内压作用下，管道所受最大应力随着初始内壁裂纹半径的增大而缓慢增大。 内壁裂纹启裂时的轴向位移及裂纹穿透管壁时的轴向位移随初始裂纹半径的增大而迅速减小，且裂纹启裂时的轴向位移和裂纹穿透管壁时的轴向位移相差较小，即裂纹启裂后扩展速度较快，极易穿透。

表2 裂纹尺寸变化时对应的应力及拉伸位移Table 2 Corresponding stress and tensile displacement when the crack size changed

3.1.2 管道内压变化对裂纹扩展的影响

根据常用天然气管道的运行内压调研，该长输管道及其站场内管道压力均在6～10 MPa 之间，因此运用ABAQUS 有限元模拟出在管道所受内压为6～10 MPa，均匀增大的拉伸位移为20 mm 的作用下，含裂纹缺陷管道所受最大应力情况，裂纹启裂及穿透时管道轴向位移结果如表3。 由表3 可知，内壁裂纹大小不变且仅在内压作用下，管道所受最大应力随着内压增大而迅速增大。 轴向拉伸作用下，随管道内压增大，内壁裂纹启裂时的拉伸位移缓慢减小，裂纹穿透管壁时的轴向位移也缓慢减小，φ273.0 mm×9.5 mm 与φ508.0 mm×6.4 mm 管道裂纹启裂时的轴向位移和裂纹穿透管壁时的轴向位移相差分别约为1.70 mm 及2.20 mm。

表3 内压变化时对应的应力及拉伸位移Table 3 Corresponding stress and tensile displacement when internal pressure changed

3.2 圆形外表面裂纹扩展影响因素分析

3.2.1 裂纹大小变化对裂纹扩展的影响

在规格为φ508.0 mm×6.4 mm 的管道中，当a＝0.5 mm 时，经模拟得出，外壁裂纹先向管道环向方向扩展，再进行壁厚方向扩展直至穿透，外壁裂纹面水平集函数云图如图8 所示，对应最大Mises 应力云图见图9。由图9 可知，管道所受最大应力处于裂纹尖端位置，对应应力为604.0 MPa，而后突然减小至591.8 MPa。

图8 管道裂纹面水平集函数云图Fig. 8 Cloud diagram of PHILSM of pipe crack surface

图9 启裂时管道对应最大Mises 应力云图(单位:MPa)Fig. 9 The maximum Mises stress cloud diagram corresponding to the pipeline when the crack was initiated

在规格为φ508.0 mm×6.4 mm 的管道中，当a＝3.0 mm 时，经模拟得出，外壁裂纹先向管道环向方向扩展，再进行壁厚方向扩展直至穿透，裂纹面水平集函数云图如图10 所示，对应最大Mises 应力云图如图11。 由图11 可知，管道所受最大应力处于裂纹尖端位置，对应应力为596.9 MPa，而后突然减小至585.7 MPa。

图10 管道裂纹面水平集函数云图Fig. 10 Cloud diagram of PHILSM of pipe crack surface

图11 启裂时管道对应最大Mises 应力云图(单位:MPa)Fig. 11 The maximum Mises stress cloud diagram corresponding to the pipeline when the crack was initiated

在均匀增大的拉伸位移为20 mm 时，运用ABAQUS 有限元模拟出管道所受内压为8 MPa 时，含外壁裂纹缺陷管道所受最大应力情况，外壁裂纹启裂及穿透时管道轴向位移结果如表4。

表4 裂纹尺寸变化时对应的应力及拉伸位移Table 4 Corresponding stress and tensile displacement when the crack size changed

由表4 可知，管道所受最大应力仅在内压作用下随着初始外壁裂纹半径的增大而缓慢增大。 外壁裂纹启裂时的轴向位移及裂纹穿透管壁时的轴向位移随初始裂纹半径的增大而迅速减小，且裂纹启裂时的轴向位移和裂纹穿透管壁时的轴向位移相差较小，即裂纹启裂后快速扩展直至穿透。

3.2.2 管道内压变化对裂纹扩展的影响

运用ABAQUS 有限元模拟出在预制裂纹大小均为a＝2 mm，仅内压变化情况下以及均匀增大的拉伸位移20 mm 情况下，含外壁裂纹缺陷管道的应力变化情况，结果如表5。

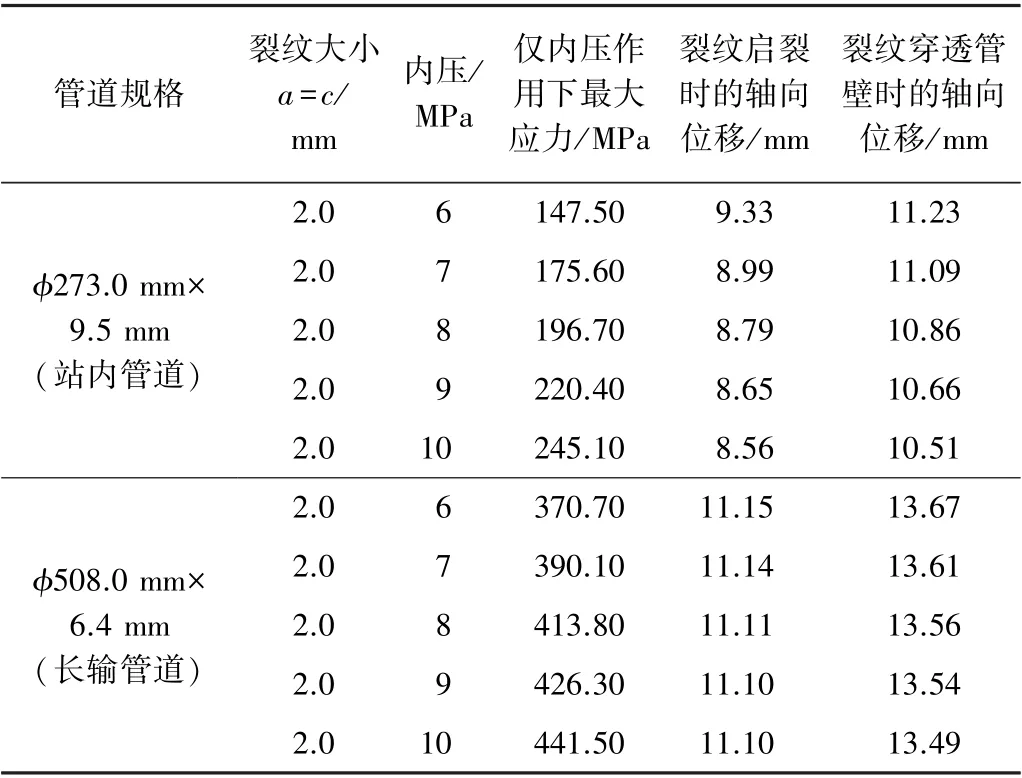
表5 内压变化时对应的应力及拉伸位移Table 5 Corresponding stress and tensile displacement when internal pressure changed

由表5 可知，外壁裂纹大小不变且仅在内压作用情况下，管道所受最大应力随着内压增大而迅速增大。轴向拉伸作用下随管道内压增大，外壁裂纹启裂时的拉伸位移缓慢减小，裂纹穿透管壁时的轴向位移也缓慢减小，φ273.0 mm×9.5 mm 与φ508.0 mm×6.4 mm 管道裂纹启裂时的轴向位移和裂纹穿透管壁时的轴向位移相差分别约为2.00 mm 及2.50 mm，相差较小，即裂纹启裂后迅速开裂至穿透管道。

3.3 圆形内、外表面裂纹扩展对比分析

3.3.1 裂纹大小变化对裂纹扩展的影响

将2 种管道仅内压作用下最大应力、启裂时的轴向位移及穿透时的轴向位移进行比较，得出结果如图12 所示。 由图12a 可知，管道仅在内压作用下时，圆形裂纹越大，管道所受的最大应力越大，增长较缓慢，且约在a≤0.3B内时，含内壁裂纹内压大于含外壁裂纹内压，裂纹继续增大则含外壁裂纹内压大于含内壁裂纹内压；由图12b、12c 可知，含圆形裂纹管道在轴向拉伸力作用下，裂纹启裂及穿透管壁时管道的轴向位移迅速下降，裂纹约在a≤0.3B时，内壁裂纹启裂及穿透管壁时的管道轴向位移小于外壁裂纹(即内壁裂纹启裂及穿透时所需要的位移/应力更小)，因此此时内壁较危险，而裂纹增大至约a＞0.3B后，外壁裂纹启裂时的管道轴向位移较小，即此时外壁裂纹更危险。

图12 圆形裂纹大小变化时对应的影响因素分析图Fig. 12 Analysis diagram of corresponding influencing factors when the size of a circular crack changed

3.3.2 管道内压变化对内、外壁裂纹扩展的影响

将2 种管道仅内压作用下最大应力、启裂时的轴向位移及穿透时的轴向位移进行比较，得出结果如图13 所示。 由图13a 可知，管道仅在内压作用下时内压越大，管道所受的最大应力迅速增大，且含内壁裂纹内压始终大于含外壁裂纹内压；由图13b、13c 可知，含圆形裂纹管道在轴向拉伸力作用下，裂纹启裂及穿透管壁时管道的轴向位移随内压增大均缓慢下降。

图13 内压变化时对应的影响因素分析图Fig. 13 Analysis diagram of corresponding influencing factors when internal pressure changed

4 结 论

通过对含表面裂纹缺陷管道的环向扩展模拟可知:

(1)管道所受最大应力处于裂纹尖端位置，启裂扩展完成之后应力有所下降。

(2)裂纹尺寸(a≤0.5B)不变时，表面圆形裂纹均先沿管道环向扩展进而沿管道壁厚方向扩展。

(3)φ273.0 mm×9.5 mm(站场管道)及φ508.0 mm×6.4 mm(长输管道)管道含内壁裂纹启裂时的轴向位移和裂纹穿透管壁时的轴向位移相差分别约为1.70 mm 及2.20 mm，含外壁裂纹启裂时的轴向位移和裂纹穿透管壁时的轴向位移相差分别约为2.00 mm 及2.50 mm，相差均较小，即裂纹启裂后很快即可穿透管道。

(4)内压为8 MPa 时，圆形裂纹越大，管道所受的最大应力缓慢增大，且在一定大小范围内含内壁裂纹内压大于含外壁裂纹内压，裂纹继续增大则含外壁裂纹内压大于含内壁裂纹内压；在轴向拉伸力作用下，裂纹启裂及穿透管壁时管道的轴向位移迅速下降，裂纹约在a≤0.3B时，内壁裂纹启裂及穿透管壁时的管道轴向位移小于外壁裂纹，而裂纹增大至约a＞0.3B后，外壁裂纹更危险。

(5)裂纹大小a＝2.0 mm 时，随着内压变大，仅在内压作用下时管道最大应力呈线性增长，在轴向拉伸力作用下，裂纹启裂及穿透管壁时管道的轴向位移随内压增大均缓慢下降。

综上所述，含表面裂纹缺陷管道的环向扩展与表面裂纹所处的位置、裂纹的大小及管道内压均有关系，其中管道内压对裂纹扩展的影响较小。 将影响因素对扩展时的拉伸位移的影响大小进行排序，结果为:裂纹尺寸＞裂纹所处位置＞内压。 本工作仅对环向圆形表面裂纹对管道扩展的影响进行了初步研究，接下来可重点研究焊缝参数对管道扩展的影响。