基于Shader 的CSG 几何体的实时渲染*

陈国军 尹 鹏 裴利强 尹 冲

（中国石油大学（华东）计算机科学与技术学院 青岛 266580）

1 引言

随着计算机图形应用的发展，布尔运算在建模系统中扮演了关键的角色［1］。经过数十年的研究和发展，二维图形和三维实体布尔运算已经成为了计算机图形学方面非常热门的研究方向之一［2］。布尔运算是通过对两个以上的物体进行并集、差集、交集的运算，从而得到新的物体［3～4］。其运算方式有并集、交集和差集。目前基于物体空间的布尔运算算法已有相当的研究成果。根据维度布尔运算分成二维布尔运算和三维布尔运算［5～6］。

二维布尔运算方法大多将几何体看成一个或多个环的组合。Feito and Rivero 将复杂多边形分解为多个三角形的组合，采用简单块链表达每一个多边形，但是涉及到奇异情况时，算法无法保证布尔运算系统的稳定性［7］。目前三维布尔运算主要通过构造实体几何（CSG）的方式完成布尔运算。构造实体几何（CSG）的基本思想是通过对基本图元如球、圆柱体、立方体等进行刚性变换和布尔运算生成复杂的模型［8～9］。Jansen 等提出了模型的阴影计算算法，他对每一个CSG体元相对CSG树生成一个阴影树，而整体CSG构造的物体产生的阴影则是整个阴影树的并集，这样可以使由CSG构造方法生成的三维物体在虚拟环境中更加真实［10］。V.S.Alagar 等提出了作为应用最为广泛的CSG 树实体建模法在CAD 系统中的重要性，并且表述了利用CSG 树的方法来构建实体模型的方法［11］。但由于表示受体素的种类和对体素操作的种类的限制，使得它表示形体的覆盖域有较大的局限性，稳定性较差。OpenCSG 是目前使用最为广泛的基于图像CSG的库，CSG使用OpenGL渲染［1，9］。

综上所述，目前几何图形布尔运算在判断两几何体相交或者重合的临界交点上容易出现误差，计算稳定性较差；当数据量较大时，顶点或者三角片数据庞大，会使得运算的计算效率降低［12］。针对以上问题，提出基于Shader 的CSG 几何体的实时渲染，利用GPU 的并行运算能力［13～14］，通过Shader 着色器处理待渲染数据。在三维运算过程中使用CSG 基元模型进行布尔运算，称之为Shader-CSG算法，可以有效解决布尔运算渲染过程出现的稳定性和实时性问题。

2 布尔运算基元建模

2.1 基元模型构建

CSG 的基元模型为球体、立方体、圆柱体等相对规则的形体。首先通过对基元模型设立通用参数来控制体元的位置、大小等属性，改变其参数可以得到基元模型的各种尺寸方向的效果。然后通过离散化，以密集三角片逼近模型的表面。

1）参数化建模

模型参数为centerPos（中心点坐标）。变换参数为length（长度）、angle（旋转角）、radius（半径）、height（高度）。

2）离散化

对于立方体，其六个表面分别由两个大小相同的三角片组成。圆柱体曲面部分是通过对圆柱底面的圆进行“分片（slices）”，每片都为角度相同的扇形，然后连接底面与顶面扇形，侧面为长方形，分成两个三角片。

球体曲面建立是通过对球体沿着Z 坐标轴旋转“分片（slices）”，在每片上再进行“分块（stacks）”。如图1 所示，分别展示了圆柱体底面分片和球体分片、分区的过程。

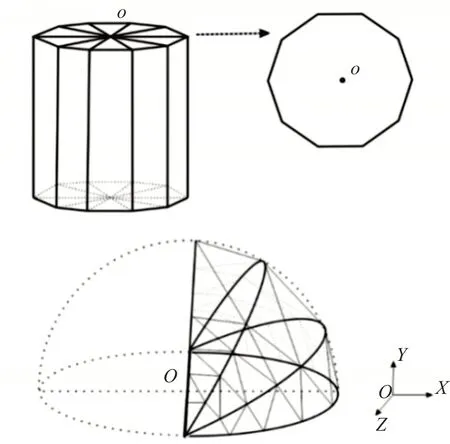
图1 基元模型离散化示意图

每个三维模型表面都通过密集的三角片进行逼近，并且保证基元模型在每个二维坐标系下的投影都是规范图形，使得在考虑误差时可以通过数学计算减小误差。

2.2 基元模型中点与几何体位置关系判断

对于三维几何体，当基元模型为立方体时，设立方体X、Y、Z 坐标系中的最大值和最小值分别为maxX、maxY、maxZ 和minX、minY、minZ。对于任意空间一点P（x，y），满足点P在立方体内部或表面的条件为

图2 点与曲面体位置关系判断图

联立方程（2）和方程（3），即可求出点解出x，y，z，得到交点V（x，y，z），通过比较VO与PO的长度：

由线段长度比较得到该点所在的位置：

3 CSG几何体的渲染

要实现CSG相对应几何体的渲染，首先要解析CSG 树，形成一个可判断的逻辑公式［15］，然后将解析结果传递到Shader（着色器）中，实现实时绘制。

3.1 布尔运算表达式解析

解析布尔运算表达式的基础是解析两个布尔基元的运算。首先针对立方体、球体、圆柱体这三种布尔运算基元，定义S1、S2、S3 分别为空间任一点与立方体、球体、圆柱体的位置关系值。例如球体，当S2=0 时，指该点在球体内部；当S2=1 时，指该点在球体表面；当S2=2 时，指该点在球体外部。将这种关系与式（5）结合，点与球体关系如式（6）所示：

当出现两个基元布尔运算时，比如立方体与球体，其交、并、差的表达式可以解析逻辑表达式。逻辑式（7）、（8）、（9）分别表示了立方体与球体的交、并、差运算。

布尔表达式中运算符，按照优先级分为括号和逻辑运算符。逻辑运算符交、并、差即可表示成”∧”、”∨”、”¬”的形式。布尔运算文法如下：

布尔表达式的解析类似算术表达式解析，其三中逻辑运算可以做以下等价解释：

对于布尔运算表达式“Q=A∩B-C”，设A、B、C 分别代指立方体、球体和圆柱体，S1、S2、S3 分别代表空间任一点与立方体、球体、圆柱体的位置关系值。通过式（7）、（8）、（9）其表达式可翻译为“Q=S1 ＜2 ∧S2 ＜2 ∧S3 ≥1”，设该表达式有两个出口Q1、Q2，经过解析，可得四元式序列：

解析入口为（101），其出口为（106）和（107），Q1为“真”出口，对应的操作为“绘制”；Q2为“假”出口，对应的操作为“丢弃”。即表达式状态只有两种：TURE 或FALSE，当为TURE 时，说明该点（像素）是符合表达式要求的，则进行渲染；当为FALSE时，说明该点（像素）是不符合表达式要求的，则进行丢弃（不进行渲染）。最后渲染的结果就是表达式的结果。

3.2 Shader着色器的工作流程

基元模型绘制是通过GLSL 绘制管线来完成的。GLSL 渲染管线也称为渲染流水线，是显示芯片内部处理图形信号相互独立的并行处理单元。一个流水线是一序列可以并行和按照固定顺序进行的阶段。

在OpenGL 中，会用到不同的四种不同的着色阶段，其中最常用的就是顶点着色器和片源着色器，前者处理顶点数据，后者处理光栅化的片元数据。Shader（着色器）实际上就是一小段程序，顶点Shader是处理顶点数据的着色器，内存中的顶点数据通过绑定VBO（顶点缓存对象）和VAO（顶点数组对象）传递到顶点Shader 中，以指定的方式和输入的贴图或者颜色等组合起来，然后输出。经过处理的顶点数据在光栅化后会以片段的形式传输到片段Shader中，通过在片段Shader中定义一系列片段处理操作最终输出片段的颜色。其流程如图3所示。

图3 Shader处理数据流程图

首先在片段Shader 中定义点与几何体的位置关系判断函数即几何函数，当表达式解析完毕并生成相应的四元式后，将四元式中的操作数集合S｛S1，S2，S3……｝与球体、立方体、圆柱体几何函数对应，其映射关系可以通过uniform 变量实现，uniform 变量可以将程序内定义的每个操作数类型传递到片段Shader中。

然后对于每一个四元式操作，都生成一个暂时的bool 类型变量T｛T1，T2，T3……｝，该变量不作为片段Shader 的输出，只作为计算过程中的数据传递。其最终运算结果即为所有中间变量的“与”运算，令Q 为最终结果即“Q=T1&T2&T3&…Tn” 。由于是bool 类型数据运算，结果为0 或者1。当结果为0，则丢弃该片段；当结果为1，则输出该片段，作为要绘制的片段部分。

4 实验结果与分析

实验平台为Intel（R）Core（TM）i3 CPU 550，主频为3.20GHz，系统内存为8GB 显卡为NVIDIA Ge-Force 730，显卡内存为1GB，操作系统为Windows 10，实验开发环境为Visual Studio 2015。实验对比了OpenCSG 和Shader-CSG 的几何图形布尔运算的渲染结果。

4.1 布尔运算效果比较

选用OpenCSG 中基本几何基元立方体、球体和圆柱体作为布尔运算的基元模型，对比OpenCSG方法和Shader-CSG 方法的基本布尔运算：交和差，并对其他复杂表达式进行了渲染。交、差运算渲染效果对比如图4、图5所示。

如图4、图5所示，左为OpenCSG实现的立方体与球体交、差运算的渲染效果，右为Shader-CSG 实现的立方体与球体交、差运算的渲染效果。

图4 交运算效果图对比

图5 差运算效果图对比

通过以上的渲染效果比较可以看出，当通过参数化建模时，基于Shader的几何图形布尔运算的渲染效果和OpenCSG 基本基元布尔运算的效果相同。图6 为几种布尔表达式下Shader-CSG 的渲染效果。

图6 Shader-CSG布尔表达式渲染效果

渲染效果表明，Shader-CSG 方法渲染效果可与OpenCSG 渲染效果相一致，能准确地呈现表达式的结果。

4.2 布尔运算效率比较

本实验比较OpenCSG 布尔运算和Shader-CSG布尔运算的渲染效率。 首先固定三角片数量，球体和圆柱体三角片数为100*100，通过增加参与布尔运算的几何体数量来统计两种方法的渲染效率。其渲染效率对比和趋势如图7所示。

图7 不同几何体数量渲染效率趋势

通过图7 可以得出，当三角片数量固定，几何体数量增加时，Shader-CSG 的渲染优于OpenCSG的渲染效率，其效率差距随着几何体数量增长而变大，表明在此条件下GPU 处理布尔运算的渲染速度更快。

然后选择表达式“A∩B-C”，通过改变三角片数量来统计两种方法的渲染效率。其渲染效率对比和趋势如图8所示。

图8 不同三角片数量渲染效率趋势

通过图8 可以得出，当几何体数量固定，三角片数量增加时，Shader-CSG 的渲染效率大大优于OpenCSG的渲染效率，当三角片个数达到百万级别时，其效率差距呈降低趋势。

结果表明，Shader-CSG 方法在渲染效果上具有很高的精确度，能稳定地将布尔表达式的结果直接的呈现出来。同时，由于其GPU 编程的特性Shader-CSG 方法在渲染效率上优于OpenCSG 的渲染效率，减少了渲染时间。

5 结语

针对传统几何图形的布尔运算的稳定性不足和绘制效率低下问题，本文提出一种基于Shader的CSG 几何体的实时渲染，通过参数化建模，用离散化的三角片绘制基元模型，并计算每个点与几何体位置关系，最后对布尔运算表达式解析将布尔运算的最终结果绘制。实验表明，该方法在绘制效果与绘制效率上具有良好的表现，并在绘制效率上优于经典的CSG（构造实体几何）绘制方式。