Banach代数中的p群逆
周心悦,刘大勇,陈焕艮
(1.杭州师范大学数学学院,浙江 杭州 311121;2.中南林业科技大学理学院,湖南 长沙 410004)
0 引言
自从Drazin逆被引入以来,多方学者对其进行了研究,并将其进一步推广,从而推进了广义逆理论的发展.1996年,Koliha在[1]中引入了广义Drazin逆.2012年,Wang在[2]中引入了一种介于Drazin与广义Drazin逆的广义逆,称为伪Drazin逆.从文[3-12]中可以看到,在这些广义逆的研究中,往往最终聚焦到对于算子矩阵的广义逆研究.
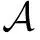
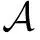
ax=xa,x=x2a,ak+1x=ak,
(1)
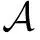
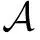
ax=xa,xax=x,axa=a.
(2)
方程(1)等价于
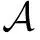
令
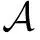
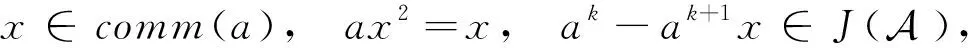
(5)
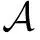
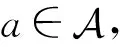
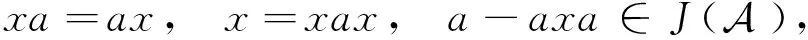
(6)
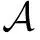
在Banach代数中,我们引进了p群逆,并研究了其相关的各种性质,进而对指标为1的p-Drazin逆进行了新刻画.
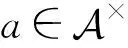
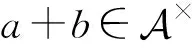
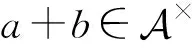
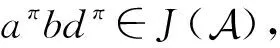
1 基本性质
方程(6)中的解x若存在,则是唯一的,写作a×.根据定义,x是a的p-Drazin逆,由文[2],所以是唯一的.
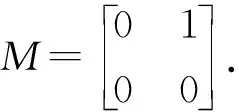
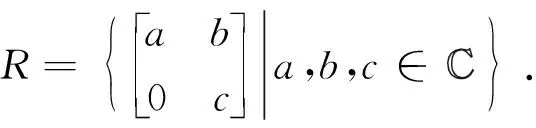
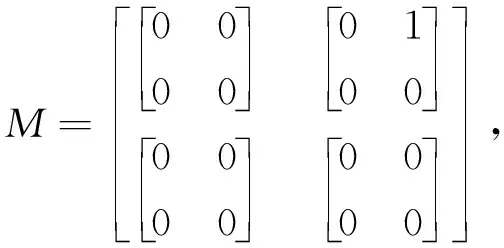
可得M×=0.但M没有群逆,因为对于任意可与M交换的矩阵X,M-MXM=M≠0.
□
由上述并结合文[2],容易得到关系:
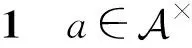
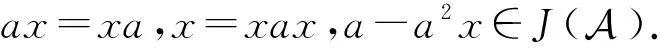
e2=(1-ax)2=1-ax-ax+axax=1-ax=e.
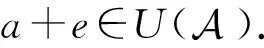
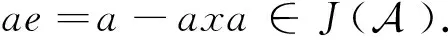
xa=(a+e)-1(1-e)a=(a+e)-1a(1-e)=a(a+e)-1(1-e)=ax.
xax=(a+e)-1(1-e)a(a+e)-1(1-e)=
(a+e)-1(1-e)(a+e)(a+e)-1(1-e)=
(a+e)-1(1-e)(1-e)=(a+e)-1(1-e)=x.
□
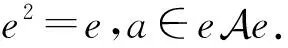
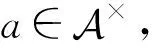
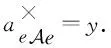
□
2 p群可逆的和问题
本节的目的是研究Banach代数中两个p群可逆元素的和何时具有p群逆.
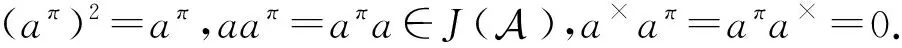
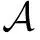
证明令
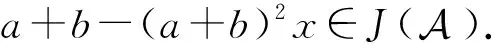
令
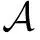
因此有
a+b-(a+b)2x=(a+b)[1-(a+b)x]=(a+b)(1-bb×aπ-abπa×)-(a+b)y=
a-a2bπa×+b-b2b×aπ-babπa×-(a+b)y=
a-a2a×+b-b2b×+b2b×aa×-baa×-(a+b)y=
a-a2a×+b-b2b×-(b-b2b×)aa×-(a+b)y,
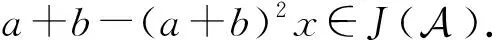
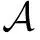
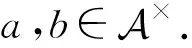
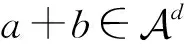
(1+adb)d=aπ+a2ad(a+b)d.
(1+adb)-(1+adb)(1+adb)d=(1+adb)[1-(1+adb)(aπ+a2ad(a+b)d)]=
(1+adb)[1-aπ-a2ad(a+b)d-adba2ad(a+b)d]=
(1+adb)[aad-a2ad(a+b)d-aadb(a+b)d]=
(1+adb){aad[1-(a+b)(a+b)d]}=
(aad+adb)[1-(a+b)(a+b)d]=
(⟸)根据[3,定理6.22]和ab=ba,我们有
只需核实
(a+b)-(a+b)2(a+b)d=
(a+b)[1-aad(1+adb)d-bad(1+adb)d-
(a+b)[1-aad(1+adb)d-bad(1+adb)d-bbdaπ]=
a+b-bbdaπa-b2bdaπ-(a2ad+baad+aadb+b2ad)(1+adb)d=
a+b-bbdaπa-b2bdaπ-ad(a+b)2(1+adb)d=
a+b-bbdaπa-b2bdaπ-a2ad(1+adb)2(1+adb)d=
a+b-bbdaπa-b2bdaπ+a2ad[(1+adb)-(1+adb)2(1+adb)d]-a2ad(1+adb)=
a+b-bbdaπa-b2bdaπ+a2ad[(1+adb)-(1+adb)2(1+adb)d]-a2ad-aadb=
a-a2ad-bbdaπa+b-b2bd+b2bd-b2bdaπ-aadb+a2ad[(1+adb)-(1+adb)2(1+adb)d]=
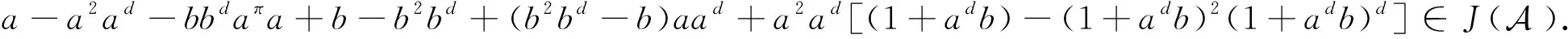
□
3 算子矩阵
本节主要研究2×2算子矩阵何时具有p群逆,我们有:
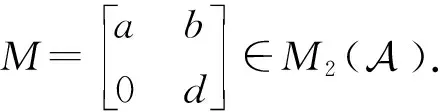
证明显然M有g-Drazin逆且
这里
那么MMd=MdM,Md=MdMMd.
只需验证
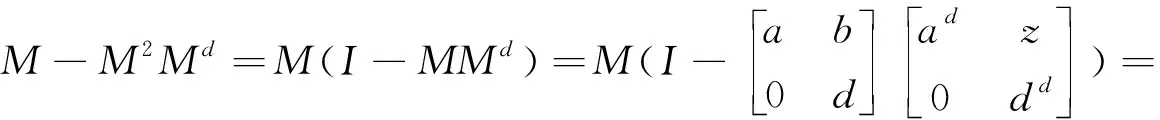
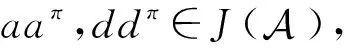
可验证
-a2z-abdd+bdπ=
因此M×=Md.
□
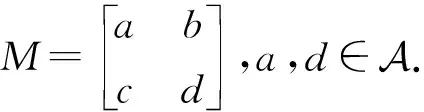
□
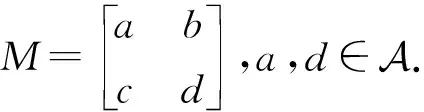
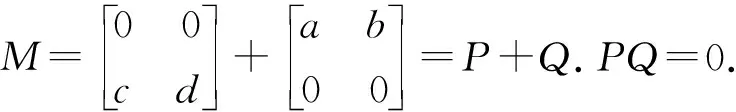
□
进一步,我们还有:
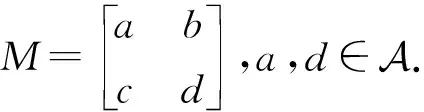
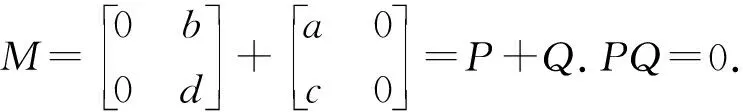
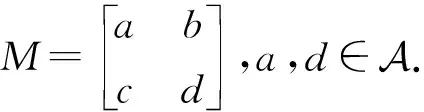
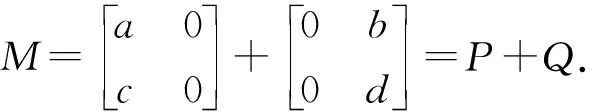
□

