基于VAR的新疆葡萄种植面积和产量预测
舒服华
(武汉理工大学继续教育学院,湖北 武汉 430070)
葡萄富含葡萄糖、氨基酸、维生素、有机酸等对人体健康有益的多种营养成分,是水果中的佳品,也是民众普遍喜爱食用的水果。其用来制作葡萄干,口味更好,营养价值更高,对身体更有益。除营养价值外,葡萄还具有一定的药用功效。此外,葡萄酿成酒,细腻绵柔、馨香四溢,且风靡全球。目前,我国是世界第三大葡萄种植国,第六大葡萄酒生产国,第二大葡萄酒消费国,2020年我国已成为全球第五大葡萄酒进口国。可见,葡萄产业在我国发展潜力巨大,前景广阔。新疆维吾尔自治区(下文简称新疆)是我国葡萄主要产区,当地土壤多为沙质,透气性良好,氧化作用强,有利于葡萄的受热和散热;地处高海拔地区,冬季温度又很低,害虫不易越冬;昼长夜短,光照充足,昼夜温差大,有利于葡萄糖分的积累[1-3]。这些得天独厚的地理气候条件十分有利于葡萄种植,也造就新疆生产的葡萄品质优良,口感绝佳。当前,新疆葡萄产量占全国25%以上,葡萄干占75%左右,葡萄酒占20%[4,5]。葡萄已成为新疆的一张名片和最具影响力的农业特色产业,对推动当地经济发展,带动农民增收致富发挥重要作用。葡萄产量与种植面积有密切关系,因此,将这两个指标联系在一起研究更有价值和意义。向量自回归模型(VAR)常用于多个相关联时间序的预测,它以历史数据为基础,通过挖掘系统内部所隐含信息对时间序列未来的发展趋势进行判断,并能揭示关联时间序列间的联系,比孤立地对多时间系列进行单独预测具有更高的精度,更客观、可信[6-13]。本研究充分发挥VAR模型的特点和优势对新疆葡萄产量和葡萄种植面积进行预测,以科学预测新疆葡萄产量,对当地制定葡萄产业发展战略规划,优化农业产业结构,做优做特葡萄产业,助力乡村振兴,拓展农民增收渠道具有重要意义。
1 VAR模型预测方法
VAR模型常用于对2个或多个相关联的时间系列的预测,一般可表示为限制性向量自回归模型[6,7]:
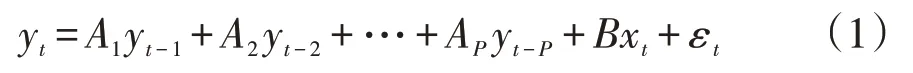
式中,yt为n维内生向量;xt为m维外生向量;εt为n维随机扰动向量;Ai(i=1,2,…,p)和B为系数矩阵。
当外生向量为常数矩阵C时,VAR模型变为非限制性向量自回归模型[7,8]:

2 新疆葡萄产量和种植面积预测
如图1所示可知,,在过去16年,新疆葡萄种植面积和产量稳中有升,前期主要呈增长趋势。由于脱贫需要,近些年新疆把重点放在发展经济效益更高的农业产业上,如畜牧养殖、其它高端瓜果业等。因此,葡萄种植面积和产量增幅放缓,基本保持稳定。将新疆葡萄种植面积设为内生变量y1,葡萄产量设为内生变量y2,由y1、y2组成二维向量时间序列Y=(y1,y2),以这16年Y序列数据为样本,建立VAR预测模型。
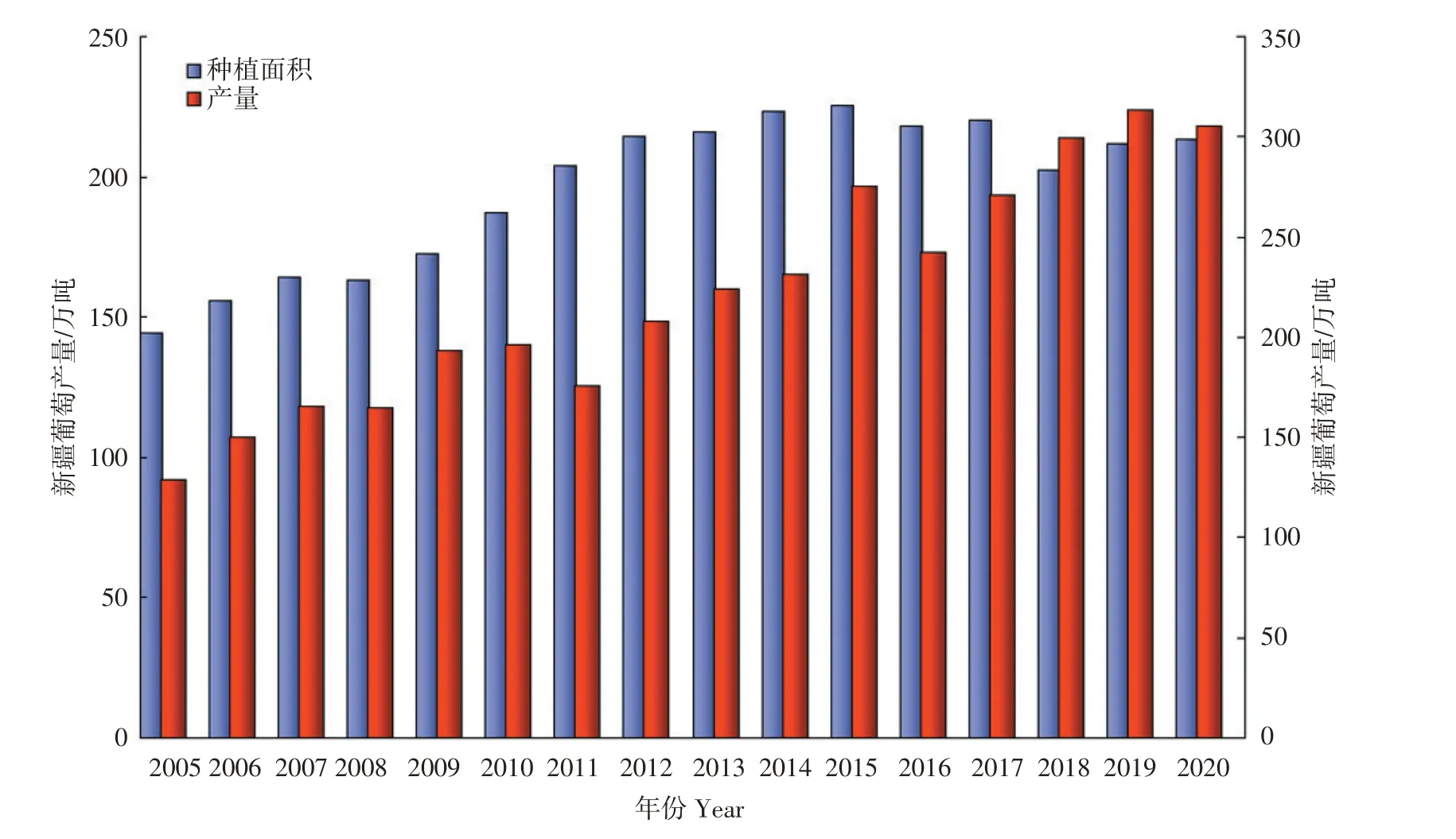
图1 新疆葡萄种植面积和产量(数据来自新疆农业农村厅)Figure 1 Acreage and yield of grape in Xinjiang(The data comes from the Xinjiang Agriculture and Rural Affairs Department)
2.1 单位根检验T
单位根检验的目的是判断序列是否为平稳序列,否则容易导致伪回归。如果序列为非平稳序列,可通过一次或多次差分使其变为平稳序列,若序列通过n次差分后才变为平稳序列,则称其为n阶单整。如表1所列可知,y1的ADF值为0.429683,大于1%、5%、10%的临界值,y2的ADF值为-2.240593大于1%、5%、10%的临界值,表明y1、y2均为非平稳序列。故对y1、y2进行一次差分,则d(y1)的ADF值为-4.827632,小于1%、5%、10%临界值,d(y1)为平稳时间系列,d(y2)的ADF值为-2.955577小于10%临界值,d(y2)也为平稳时间序列,y1、y2经过一次差分后,皆变为平稳系列,即内生变量y1、y2为一阶单整,满足协整检验的条件。初步建立模型VAR(2),以检验d(y1)、d(y2)协整性、格兰杰因果关系、模型的最佳滞后期。
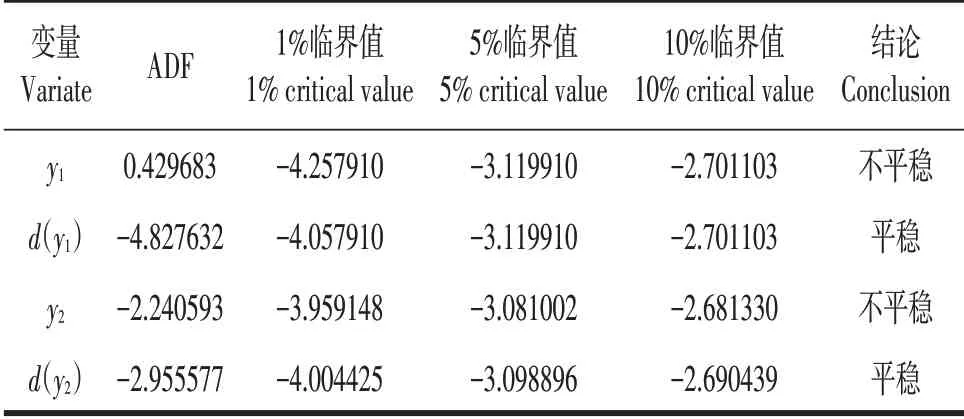
表1 单位根检验结果Table 1 Unit root test results
2.2 协整性检验
协整性检验主要是考察所研究变量组是否存在长期的均衡关系,只有存在一定的联系,将它们联合起来研究才有意义。如表2所列可知,对于“无协整性”假设,似然概率为0.0015,小于5%的置信水平,故拒绝原假设;对于“最多一个协整关系”假设,似然概率为0.0738,大于5%的置信水平,故接受原假设。说明二者存在一个协整关系,即葡萄的种植面积与产量存在长期的均衡关系,将它们一同研究是有意义的。

表2 协整性检验结果Table 2 cointegration test results
2.3 格兰杰检验
对d(y1)、d(y2)进行格兰杰检验,在滞后2阶的条件下,结果如表3所列可知,两个假设的显著性概率都大于5%的置信水平,故均接受原假设,即d(y1)与d(y2)间双向不存在格兰杰因果关系。值得注意的是,格兰杰因果关系并非现实生活中的因果关系,而是统计学上的因果关系,它仅说明在短期内,一个变量的变化对另一个变量的变化解释的有利性。所以,这不代表葡萄的产量和种植面积间没有关系,而只是在短时期内,二者的变化不一定立刻一一对应。这也是可理解的,如葡萄种植面积一时的增减,有时并不能马上影响葡萄产量的增减,如种子、种植结构、旱涝等自然灾害、病虫害、管理技术等,都会导致葡萄单产的不确定性,总产量的变化就很难说得准。即在短期内,葡萄产量不一定随种植面积同步变化。
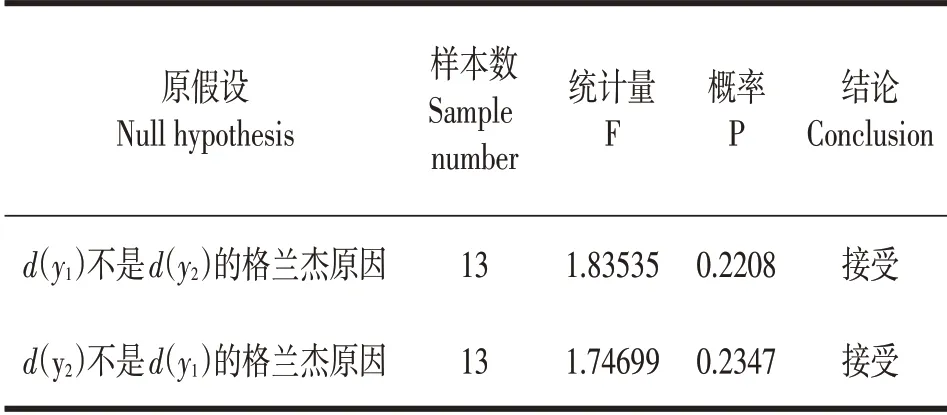
表3 格兰杰检验结果Table 3 Granger test results
2.4 模型滞后阶数确定
滞后阶确定一般以赤池信息准则(AIC)值和施瓦兹准则(SC)值最小为原则。当AIC值、SC值不在同一滞后阶最小时,则以似然比统计量(LR)值最大为准则。滞后阶数越大,模型的自由度越小,模型的参数越多、越复杂,并不能得到好的预测效果,对于样本容量不大于时间序列,滞后期在3以内考察基本可满足。模型滞后阶判别如表4所列可知,在考察的3个滞后阶中,AIC值在滞后3期最小,SC值在滞后0期最小。因此,需要根据LR值确定最佳滞后期。LR在滞后2阶最大,故最佳滞后期应为2,但由于两个变量都进行过一次差分,实际的滞后期应是名义滞后期加上差分的次数,所以最佳滞后期最终应为3,即模型最佳阶数p=3,因此确定的模型为VAR(3)。

表4 模型滞后阶判别结果Table 4 Judgment results of model lag order
2.5 参数估计
建立VAR(3)模型后对模型的参数进行估计,结果如图2所示,其中,参数第一项为系数,第二项为标准差(带小括号),第三项t统计量(带方括号)。根据估计的参数得到预测方程式(3),即新疆葡萄种植面积和产量的VAR预测方程。

图2 模型的参数估计结果Figure 2 Parameter estimation results of the model

2.6 稳健性检验
对建立的VAR(3)模型进行稳健性检验,结果如图3所示可知,模型的6个特征值都位于单位圆内,即所有特征根模的倒数都小于1,说明模型是稳定和可靠的,可用于序列组的预测。

图3 模型的稳健性检验结果Figure 3 Robustness test results of the model
2.7 变量预测
根据预测方程(3)对新疆葡萄的种植面积和产量进行预测,结果如表5所列可知(由于数据进行了一次差分处理,且后期值、前期值和预测误差有关,因此前4期的值不能预测),模型对葡萄种植面积和产量的平均预测误差分别为2.28772%和3.16478%,两个指标的平均预测误差都在公认的优良级标准3%左右,表明运用VAR模型预测新疆葡萄产量和种植面积不仅可行,而且效果良好。由模型预测,2021年新疆葡萄种植面积为215.4766·667hm2,产量为298.87767万吨,比2020年略有下降,两项指标基本保持稳定。考虑到新疆仍在进一步推进葡萄产业的发展,2021年葡萄种植面积会小幅增加;而2021年全国大多数地区气候反常,极端天气频发,新疆也不例外,因此,对葡萄的生长有所影响,产量会出现小幅下降。可见,预测结果有较大可信度。

表5 模型预测结果及比较Table 5 Model prediction results and comparison
2.8 脉冲分析
脉冲分析方法是给模型加一个单位标准差的干扰信号,考察干扰信号运行情况。如图4所示脉冲分析可知,给d(y1)加一个d(y2)标准差大小的干扰信号,d(y1)沿着0线上下振动,均值趋于0,干扰信号随期数震荡减弱,约在第10期左右消退,最终收敛;给d(y2)加一个d(y1)标准差大小的干扰信号,d(y1)沿着0线上下宽幅振动,均值基本趋于0,干扰信号也随期数震荡减弱,收敛的期数有所延长,但应该也是收敛的。说明d(y2)受d(y1)影响较大,即葡萄产量长期来看主要受种植面积的影响。脉冲分析表明模型是合适和正确的。
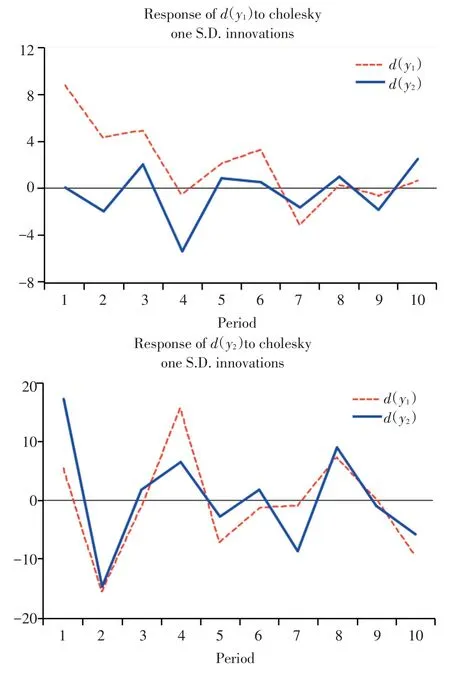
图4 脉冲分析结果Figure 4 Pulse analysis results
2.9 方差分解
由于两个变量存在协整关系,对二者进行预测牵涉到彼此之间的信息。预测精度不仅与自身有关,还与对应的另一个变量有关。方差分解的目的就是分析各变量预测误差的组成与来源。如图5所示可知,d(y1)的预测误差主要来源于本身,占80%,20%来源于d(y2);d(y2)的预测误差均匀来源于d(y1)和d(y2),二者各占50%。再次反映葡萄种植面积是决定葡萄生产的主要因素。

图5 方差分解结果Figure 5 Variance decomposition results
本研究运用VAR模型对新疆葡萄种植面积和葡萄产量进行预测,取得较好效果,葡萄种植面积平均预测误差仅为2.28772%,葡萄产量平均预测误差为3.16478%。根据模型预测,2021年新疆葡萄种植面积为215.4766·667hm2,葡萄产量为298.8776万吨。

