基于时间动态变分自编码器和逻辑正则极限学习机的变压器绕组变形故障诊断方法

郑伟钦，何胜红，钟 炜，马 欣，张 勇，张哲铭，龚令愉，谭泳岚，钟嘉燊

（广东电网有限责任公司佛山供电局 广东 佛山 528000）

0 引言

电力变压器是电力系统中最重要和最关键的电气设备之一，承担着不同电压等级电网的互联以及功率交换的枢纽作用，其可靠运行直接关系到电力系统的安全与稳定。据有关研究资料表明，绕组变形是电力变压器最主要的故障类型之一[1]。因此，对于新生产和投运的变压器，绕组具有变形的可能性和一定的隐蔽性，对电网的运行存在严重的安全隐患，积极开展绕组状态检测和故障诊断非常关键。

目前对于变压器绕组变形诊断的研究方法主要有短路阻抗法、低压脉冲法、振动分析法、发散系数法和频率响应分析法（frequency response analysis, FRA）[2-3]。其中FRA因具有试验设备便携、灵敏度高、信息丰富等优点而得到国内外电力行业的一致认可。但是这些诊断方法属于离线检测，需要结合设备停电检修进行，无法第一时间发现绕组健康状况。另外，基于FRA主要是通过横向比较变压器同一电压等级的三相绕组幅频响应特性，通过计算三相绕组频率响应曲线在低、中、高频段以及整个频段的相关系数来评估变压器绕组是否存在变形，但是该分析方法过于依赖完善的频率响应原始数据库。针对以上问题，国内外研究学者分析了绕组变形引起的频率响应机理，结合等值电路模型探究绕组变形与频率响应的关系[4-5]。但是目前这些研究对于引起变压器绕组变形的根本原因及其对应的故障类型的认识还不够系统，难以获得数量和种类丰富的故障样本，缺乏完备的绕组变形数据库。

为此，本文提出了一种基于时间动态变分自动编码器（TD-VAE）和逻辑正则极限学习机（LogRELM）的变压器绕组变形故障诊断方法。首先沿用鲁非等[4]和邹林等[5]提出的基于“结构参数—电气参数—试验结果”绕组变形故障诊断的新思路，通过变压器有限元模型模拟不同程度变压器绕组径向形变、轴向位移和绕组饼间变化3种故障，求解绕组变形时变压器主要电气参数（电容、电感）。根据所求的电气参数在Matlab软件中搭建变压器绕组等值电路模型，仿真不同绕组变形下变压器的FRA曲线，构建绕组变形故障数据库。以FRA曲线为基础，首次利用基于TD-VAE对原始FRA数据进行重构，生成与原始FRA数据相似的高质量新样本，实现数据样本的增强。同时采用粒子群优化算法（PSO）对LogRELM模型参数进行优化，构建PSO-LogRELM组合模型对变压器绕组变形类别进行诊断。实验结果表明，在绕组变形样本数据匮乏和不平衡的情况下，所提方法可以有效提高绕组变形故障诊断精度。

1 TD-VAE生成模型

针对现有电力变压器绕组变形FRA曲线识别和异常检测存在样本数据匮乏的问题，本文提出了一种基于时间动态变分自动编码器的电力变压器绕组变形频率响应曲线生成模型，学习原始变压器绕组变形FRA曲线的样本分布规律，生成与原始数据相似的高质量新样本，从而实现训练集数据增强。

1.1 标准变分自编码器

变分自编码器（VAE）是一种深度学习生成模型，其网络结构包括输入层、隐变量层和输出层[6]。变分自编码器通过建立样本的概率密度分布模型来学习样本的分布规律，模型由编码器和解码器两部分组成。在变分自编码器中，编码器用于建立原始输入数据的变分推断，生成隐变量的变分概率分布；解码器根据推断网络生成的隐变量变分概率分布，生成与原始数据接近的概率密度分布。如图1所示，编码器将原始数据编码生成隐变量z，生成网络根据隐变量z还原生成原始数据的近似概率分布。

由于隐变量z的分布未知，无法直接利用最大期望值算法进行变分推断求解（也即解码过程），因此变分自编码器模型在编码器中引入了一个识别模型，来代替无法确定的真实概率分布，这样模型就可以作为变分自编码器的编码器部分，条件分布作为解码器部分。为了使识别模型与真实的概率密度分布近似相等，变分自编码器训练过程引入了噪声，并且使隐变量的分布尽可能地靠近正态分布N（μ，σ2），其中μ为均值，σ2为方差。VAE模型的损失函数是带正则项的负对数似然函数，其表达式为：

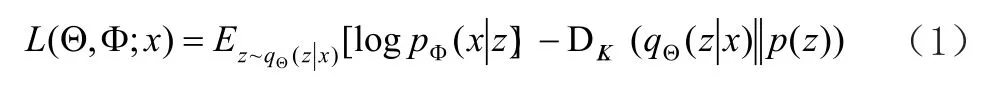
式（1）中第1项是重构损失函数，其作用是控制生成数据和原始数据尽可能相近，第2项是Kullback-LeiblerL（KL）散度，其作用是衡量生成分布与真实分布的近似程度。p（z）为先验分布，通常情况下设置为标准正态分布N(0，1)。其中，KL散度的计算公式如下：

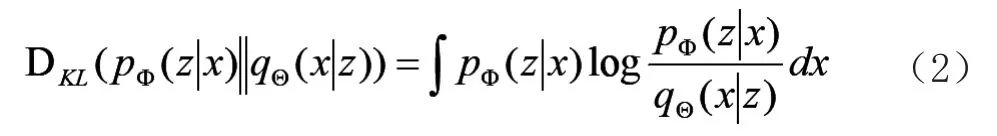
L(Θ ,Φ;x)为变分下界，通过极大似然法来求解变分下界的最大值。

1.2 标准变分自编码器

电力变压器绕组变形频率响应曲线低、中和高频段可以看作是时间序列数据，这些时间序列数据具有短暂性和动态性的特点，为了能够很好捕捉电力变压器绕组变形频率响应曲线时间序列数据的这些特点，本文提出了一种时间动态变分自编码器（Time Dynamics VAE, TD-VAE），其结构图如图1所示。

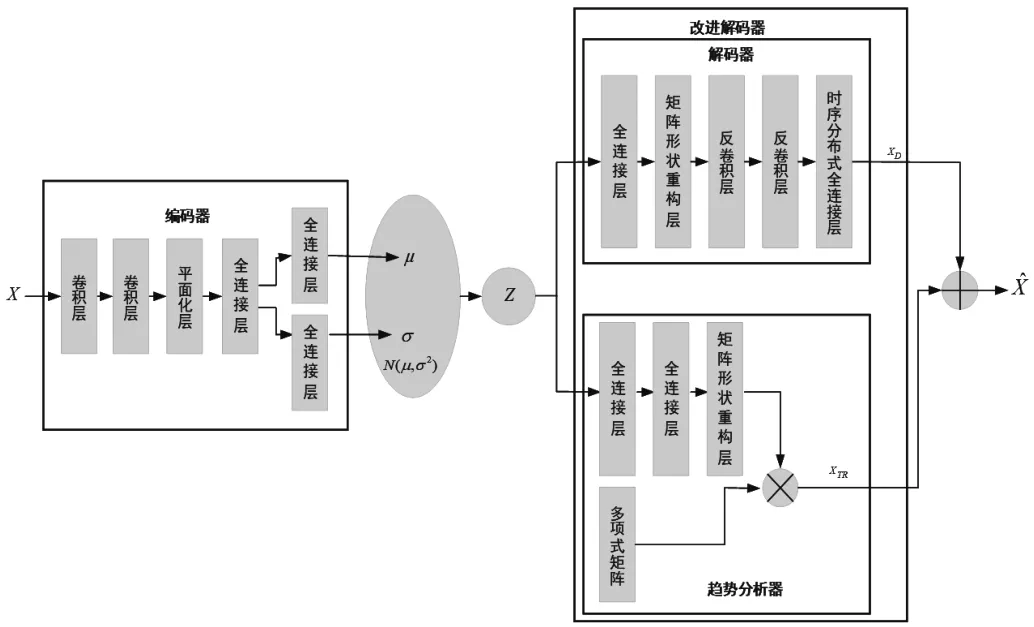
图1 时间动态变分自编码器结构图

TD-VAE模型的编码器与标准变分自编码器一样（原始编码器），解码器部分包括原始解码器和趋势分析器。原始编码器由一维卷积层、平面化层和全连接层构成，一维卷积层采用修正线性单元（Rectified linear unit，ReLU）激活函数。

假设输入模型原始编码器的电力变压器绕组变形频率响应曲线X的维度为M×T×D，其中M为批量计算中batch size的大小，T为时间序列的步长，D为每个变量的特征维度，ReLU激活函数的计算公式如下：

平面化层的作用是将输入“压平”，即把多维的输入压缩成一维。图2中，平面化层将一维卷积层的输出数据压平，然后直接输入到全连接层。

全连接层采用线性激活函数，其输出结果的达式如公式（4）所示：

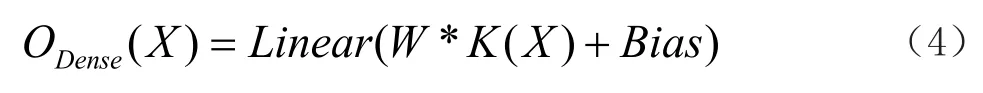
其中W为权值矩阵，K(·)为核函数，Bias为偏置矩阵，Linear(·)表示线性激活函数，其表达式为：

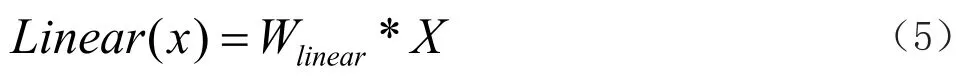
其中Wlinear为权值矩阵。

原始解码器包括全连接线性层Dense层、Reshape层、反卷积层Conv1DTransp以及时序全连接层Time-Dist Dense层。如图2所示，根据观测值X采样隐变量z，并将隐变量z输入到Dense层。Conv1DTransp层与Conv1D层的作相反，其是将Dense层的输出进行反卷积计算，此次也是采用ReLU激活函数。最后通过时序全连接层Time-Dist Dense层输出与原始输入维度一致的重构数据。

趋势分析器能够动态捕捉电力变压器绕组变形频率响应曲线的时序模式，曲线的趋势主要表现为上升、下降和平稳，并且将这种趋势反映到解码器中。利用趋势分析器对时间序列数据进行分析，能够捕捉到数据的不确定性和动态性。趋势分析器采用多项式函数表示，假设预先设置多项式的次数为p=[0 ，1，…,P]，对于根据观测值X采样得来的隐变量z，分别计p=[0 ， 1，…,P]算隐变量z的pi(i= 1 ,…,P+1)次项式的展开系数ρtr，其维度为M×D×P。接着利用多项式展开系数矩阵ρtr来建立原始输入数据的趋势模型，其表达式如下：

其中R=[1，r，...，rp]为时间矩阵r的p次幂矩阵，其维度为P×T，时间矩阵r=[0，1，2，...，T-1]，T为时间步长。多项式展开系数矩阵ρtr与r的p次幂矩阵相乘，得到匹配模型输入的矩阵格式，其维度为M×T×D。p=0时，表示时间序列数据没有出现上升或下降的趋势，时间序列趋于平稳状态，可以看成是原始时间序列的平均。

2 基于PSO-LogRELM的绕组变形诊断模型

2.1 ELM算法

标准极限学习机（ELM）算法因具有学习速度快、泛化能力强等特点而在回归问题、分类和故障诊断上得到广泛应用。ELM算法在训练时过程中随机分配输入层与隐含层之间的输入权值参数w与隐含层上的偏置参数b，在确定输入权值参数w与隐含层上的偏置参数b之后，就可以通过广义逆矩阵来对输出权值参数进行求解，标准ELM算法的训练过程具体如下：

给定一个样本量为N的绕组变形曲线训练集｛xi，yi｝（i=1，...，N），其中输入变量xi∈Rm，yi为绕组故障类别，则ELM模型可以表示为：

式中，L为隐含层神经元个数，wk=[wk1，...，wkn]T为输入层与第k个隐含层神经元之间的权值，bk为第k个隐含层神经元的偏置，wk和bk都为随机产生。βk=[β1，...，βm]T为输出层与第k个隐含层神经元之间的权值。f（x）为激活函数，且

为方便绍，将公式（7）改写为

式中，隐含层输出矩阵H和输出权值矩阵β的表达式可以参考Zhang等[7]的研究。

ELM在学习过程中是利用随机分配的输入权值参数和偏置参数来寻找最优的输出权值β。而问题的求解是转化为求解最小二范数，即

根据公式（9）可以最终求得输出权值矩阵β的解

式中，H+是H的Moore-Penrose广义逆矩阵。

2.2 LogRELM算法

ELM模型的训练机制是考虑训练误差最小化，通过最小二乘解法来求解模型最优参数。然而，这种处理方式可能会引起模型的“过拟合”问题，导致故障诊断精度降低。另外，随机分配输入层与隐含层之间的权值参数和隐含层上的偏置参数也会影响变压器绕组变形故障诊断结果。

为了解决以上问题，借鉴Tan等[8]的改进机理，本文提出了一种基于逻辑混沌映射的正则ELM（Logistic Regularized ELM，LogRELM）的变压器绕组变形故障诊断方法。引入正则化系数η来权衡模型训练误差和输出权值，对目标函数（9）进行修正：

利用拉格朗日算子求解式（11）中的最优问题，最终求得输出权值矩阵：

式中，I为单位矩阵。

为了解决ELM算法随机分配输入权值参数和偏置参数的问题，Tan等[8]提出利用逻辑混沌映射来初始化ELM算法的输入权值矩阵，其计公式如公式（13）所示。

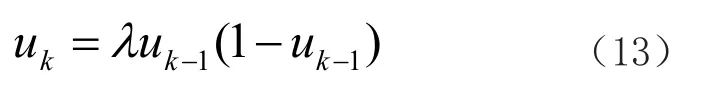
式中，u1∈(0,1)，λ为混沌系统调节系数，其经验取值范围为（3.569 95,4）时逻辑映射系统表现为混沌状。根据公式（13）可以求得输入权值矩阵如下：

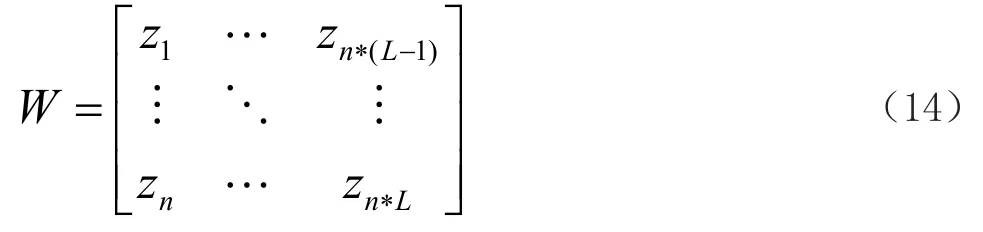
由于LogRELM算法利用混沌原理来生成模型输入矩阵，这种生成方式具有很强的随机性。因此，与标准ELM算法不同，LogRELM算法无需随机预设偏置参数，即b=0。

2.3 PSO-LogRELM模型

本文所提的LogRELM变压器绕组变形故障诊断方法中，需要考虑混沌系统初始值u1和调节系数λ，RELM算法隐含层神经元个数L和调节系数η对故障诊断精度的影响。因此，利用粒子群算法[9]（particle swarm optimization, PSO）对参数Ω=(u1,λ,L,η)进行优化，优化的目标函数为：

3 仿真分析

3.1 数据构建

本文基于实际变压器的结构尺寸及材料特性在Ansoft Maxwell中搭建了变压器有限元模型，变压器的主要电气参数来源于邹林等[5]的研究。本文以高压绕组为例，通过构建不同变形类型和变形程度的绕组有限元模型，计算绕组轴心偏移、辐向变形和饼间距变化绕组的等值电路参数。仿真模拟变压器绕组轴向形变和辐向形变时分别以绕组高度和内外径差值的1%为间隔设置变形程度，辐向变形模型采用邹林等[5]设计的4种辐向变形类型。仿真模拟变压器绕组饼间间距变化时，以正常饼间间距的1%为间距设置变形程度。根据仿真得到的等值电路参数，利用Matlab建立电路模型进行仿真，获取健康绕组和变形绕组（6种类型）的FRA曲线。

根据以上的设置，仿真模拟收集到355组绕组变形样本数据，对于每一种变形类别，随机选取样本数据的90%作为训练样本，剩下的10%作为测试样本，具体的样本分布况如表格1所示。

表1 样本数据分布

绕组变形FRA曲线具有1 000个采样点，为了更好捕捉绕组变形FRA曲线的特征和提高诊断精度，提取能反映FRA曲线的时域统计指标值作为特征向量，包括平均值、绝对值、峰值、均方根值、标准差、偏度、陡度、脉冲因子、波形因子、波峰因子、变异系数和方差。每种指标值的计算可以参考胡超等[10]的研究。

为了提高PSO-LogRELM算法的泛化能力和考虑到激活函数对预测精度的影响，将特征向量按照式（16）进行数据标准化：

式中，xi和分别为FRA曲线特征向量的原始数据和标准化后的数据，为特征向量的平均值，xmax和xmin分别为特征向量的最大值和最小值。

3.2 对比方法及参数设置

为了验证所提方法的诊断性能，本文将PSO-LogRELM模型与PSO-RELM模型、PSO-SVM模型、LogRELM模型、RELM模型以及SVM模型的诊断结果进行比较。在进行绕组变形故障诊断之前，需要对模型TD-VAE和PSO-LogELM的网络结构进行设计，各模型的参数设置如下：

（1）PSO算法参数设置：迭代次数为100代，粒子个数为20，最小误差为0.001。

（2）RELM模型参数设置：隐含层节点L个数为25，正则化系数η为25；PSO-RELM模型中，隐含层节点L的优化区间为[5,10,...,100]，正则化系数η的优化区间为[2-10,2-8，...，220]。

（3）LogRELM模型参数设置：混沌系统初始值u1=0.6，混沌系统调节系数的优化区间为0＜λ＜4；PSO-LogRELM模型中，混沌系统初始值u1的优化区间为（0,1），混沌系统调节系数λ的优化区间为（0,4），隐含层节点L的优化区间为[5,10,...,100]，正则化系数η的优化区间为[2-10,2-8，...，220]。

（4）SVM模型参数设置：采用RBF核函数，核函数参数为0.5，惩罚系数为28；PSO-SVM模型中，核函数参数的优化区间为（0,1），惩罚系数的优化区间为[2-10,2-8，...，220]。

在进行参数寻优时，利用评价指标每类准确性的平均值Eave作为PSO算法的目标函数，Eave值越大表示模型诊断精度越高，其计算公式如下：

式中，AACC,i为第i类正确分类的数量与该类别的总数的比值，T为数据集类别的总数。

3.3 实验结果分析

3.3.1 TD-VAE模型有效性验证

为了验证TD-VAE模型的有效性，利用TD-VAE生成数据样本来扩充训练数据集，从而提高诊断模型的精度。首先利用TD-VAE对每种绕组变形类别的样本数据进行扩充，为了充分对比分析，将原始训练集分别扩充20%、40%、60%和80%的数据量，扩充后的训练集分别为381、445、508和572。把扩充后的样本集来训练PSO-LogRELM模型，并对测试样本进行故障类型诊断，诊断结果的准确率如表3所示。

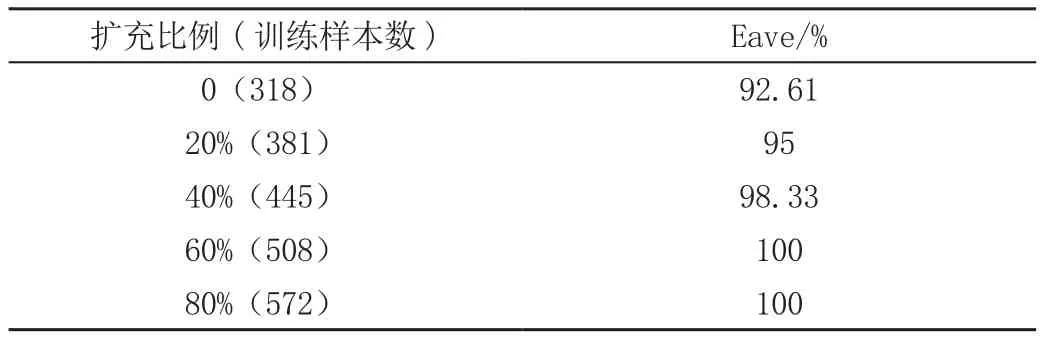
表3 不同数据扩充比例下绕组变形故障诊断精度对比

由表3和图2可以得出，（1）采用TD-VAE对原始训练集数据样本进行扩充，能够有效提高诊断模型对绕组变形故障的诊断精度，提高不平衡数据集的分类精度；（2）原始训练集数据样本扩充数据量的比例越大，诊断模型对于绕组变形故障诊断的精度越高，扩充后的精度分别提高了7.980%、7.980%、6.176%和2.581%；（3）从图2可以发现，数据扩充60%和80%时，模型PSO-LogRELM模型能够将测试样本全部诊断正确，并且对比原始数据（扩充比例为0）时仅出现3个测试样本诊断错误；（4）同时也反映出基于TD-VAE的绕组变形频率响应曲线生成模型，学习原始绕组变形FRA曲线的样本分布规律，生成与原始数据更加近似的高质量新样本，能够解决训练样本数据不平衡的问题，实现训练集数据增强。

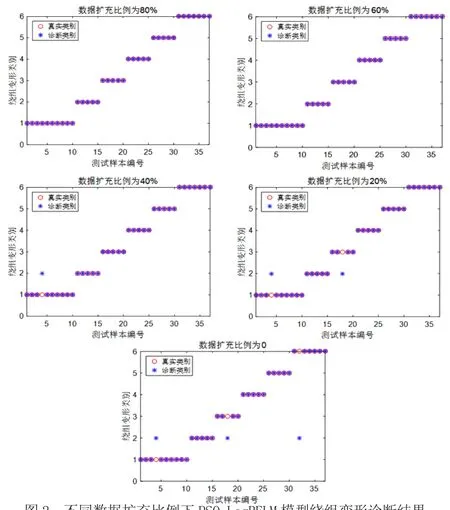
图2 不同数据扩充比例下PSO-LogRELM模型绕组变形诊断结果

3.3.2 PSO-LogRELM模型有效性验证

为验证PSO-LogRELM诊断模型的科学性和有效性，选取不同扩充比例下的训练样本搭建绕组变形诊断模型，模型包括：PSO-RELM模型、PSO-SVM模型、LogRELM模型、RELM模型以及SVM模型。测试样本的诊断结果如表4所示。

表4 不同数据扩充比例下不同模型绕组变形故障诊断精度对比

（1）由表4可以看出，PSO-LogRELM模型在不同数据扩充比例下绕组变形诊断精度都优于其他对比方法，在80%和60%扩充比例下的预测精度均为100%。

（2）相比于LogRELM、RELM、SVM模型，利用PSO算法优化后的模型诊断精度均具有更高的诊断精度。以20%扩充比例为例，PSO-LogRELM模型的诊断精度与其他模型相比，Eave值分别提高了6.41%、1.79%、10.53%和14.98%，这表明PSO算法能够有效优化模型参数，从而提高LogRELM模型的诊断精度。

（3）相比较RELM模型，本文采用的LogRELM模型无论是否经过参数优化，其绕组变形诊断精度均高于RELM模型，Eave值分别提高了2.06%、4.03%、3.74%、2.62%和3.58%。

4 结论

针对传统变压器绕组变形诊断方法无法精准确定绕组变形类型以及试验数据匮乏的问题，提出了一种基于时间动态变分自动编码器（TD-VAE）和逻辑正则极限学习机（Logistic-ELM）的变压器绕组变形故障诊断方法。通过仿真分析和实验验证，得出以下结论：

（1）利用Ansoft Maxwell软件建立变压器三维有限元模型来仿真计算变压器绕组变形（轴心偏移、辐向变形和饼间间距变化）时的主要电气参数。根据所求的电气参数在Matlab搭建变压器绕组等值电路模型，模拟仿真不同绕组变形下变压器的频率响应曲线。

（2）在模型训练前，利用TD-VAE算法预先学习原始数据的真实分布，通过生成与原始数据相似的样本来扩充训练集，减少各类样本之间的不平衡度，有效地提高模型对少数类样本的识别能力。

（3）对比其他诊断模型，所提的基于TD-VAE和PSOLogRELM模型具有更高的诊断精度，在解决少数样本情况下变压器绕组变形故障诊断问题上提供了一种新思路，具有一定的参考价值。