On the stability of small-scale ballooning modes in axisymmetric mirror traps
Igor KOTELNIKOV, Andrej LIZUNOV and Qi usun ZENG
1 Budker Institute of Nuclear Physics SB RAS, Novosibirsk, 630090, Russia
2 Novosibirsk State University, Novosibirsk, 630090, Russia
3 Institute of Nuclear Energy Safety Technology HFIPS CAS, Hefei, 230031, People’s Republic of China
Abstract It is shown that a steepening of the radial plasma pressure profile leads to a decrease in the critical value of beta, above which, small-scale balloon-type perturbations in a mirror trap become unstable.This may mean that small-scale ballooning instability leads to a smoothing of the radial plasma profile.The critical beta values for the real magnetic field of the gas-dynamic trap and various plasma pressure radial profiles was also calculated.For a plasma with a parabolic profile critical beta is evaluated at the level of 0.72.A previous theoretical prediction for this trap was almost two times lower than maximal beta 0.6 achieved experimentally.
Keywords: mirror trap, ballooning modes, critical beta
1.Introduction
There are a number of publications related to the stability of ballooning MHD perturbations in mirror traps(also called open traps) [1–34].Most were published in the 1980s.In following decades, interest in the problem of ballooning instability in mirror traps significantly weakened (in contrast to what is happening in tokamaks, see e.g.[35–37]), which was a consequence of the termination of the TMX (Tandem Mirror eXperiment) and MFTF-B (Mirror Fusion Test Facility B)projects in the USA in 1986[38].However,the achievement of a high electron temperature and high beta (β, the ratio of the plasma pressure to the magnetic field pressure) in the Gas-Dynamic Trap (GDT) at the Budker Institute of Nuclear Physics in Novosibirsk [39–47] and the emergence of new ideas[48] and new projects [49, 50] makes us rethink old results.
There was also a specific occasion for a critical revisiting of early publications.Long-term calculations of the stability boundary of ballooning vibrations in the GDT with realistic profiles of the magnetic field predicted the maximum achievable beta almost two times lower [2] than that was later achieved with this facility [39–41].In the present paper, we eliminate the contradiction between the theory and experiment.
To achieve this goal we turn to the study of the small-scale ballooning perturbations in axisymmetric mirror trap.Such perturbations are characterized by large values of the azimuthal wave number m ≫1.In addition, we restrict ourselves to the paraxial approximation, assuming that the transverse size a of the plasma in the trap is small compared to its length L,a ≪L.Attempts to calculate the equilibrium and stability of nonparaxial systems were made by Vladimir Arsenin et al[13–18],however, no quantitative predictions have been made.
In our research, we use the canonical method for studying ballooning instability, historically associated with the energy principle in the approximation of one-fluid ideal magnetohydrodynamics [7].It should be understood that this method has limited applicability.In particular,it assumes that in equilibrium the plasma is stationary,that is,it does not rotate around its axis and does not flow out through magnetic mirrors.In addition,the energy principle ignores the effects of a finite Larmor radius(FLR effects) [19–21], which should stabilize small-scale flute and ballooning perturbations with m>a2/(Lρi) (ρiis the ion Larmor radius) [22].Nevertheless, even with the listed limitations, the energy principle allows important conclusions to be drawn.In particular,based on our analysis showing that smaller scale instabilities would be unstable while larger scale would not,we infer that small-scale ballooning instability leads to a smoothing (unsteepening) of the radial plasma pressure profile.
First part of the following study is based on a simplified derivation of the equation for ballooning oscillations from the energy principle performed by Dmitri Ryutov and Gennady Stupakov [1].The simplification includes (a) the use of the paraxial approximation, and (b) the use of the low beta approximation, β ≪1, which allows us to assume that the magnetic field both inside and outside the plasma column is close to the vacuum one.
A more accurate calculation, which used only the first(paraxial) approximation (a) and therefore valid even for the case β ~1, was made by Ol’ga Bushkova and Vladimir Mirnov [2].These authors used the ballooning equation that was derived by William Newcomb in[3].The same equation with a short derivation is given in[6]for the case of isotropic plasma.It has been studied in [4], and the effect of strong anisotropy created by a rigid ring of electrons has been included into consideration in [5].
In this paper, we revisit some of the previously established results concerning ballooning instability in axially symmetric paraxial mirror traps,with an emphasis on the effect of the radial pressure profile on the maximum attainable plasma beta.In what follows, we will adhere to the following order of presentation.The equation for ballooning oscillations in the low-pressure plasma limit(β ≪1)is written in section 2.Its solutions for some model magnetic field and pressure profiles are presented in section 3.Here the critical value of normalized pressure gradientβcritis calculated, above which ballooning disturbances become unstable.Parameterβis proportional to conventional betaβ0=8πp0B02(defnied as the ratio of plasma pressure p0to the magnetic feild pressureB028πon the system axis) and normalized pressure gradient (r/p0)(dp/dr) properly averaged over the perturbation profile.It turned out that the calculated values ofβcritin some cases exceeds one.This means that the assumption β0≪1, made when deriving the simplified equation, does not hold for less steep pressure profiles.Nevertheless, the low-pressure plasma approximation gives a quantitatively correct result for a plasma with a radial pressure profile close to a stepwise one,for which the critical value β0critof conventional beta is small.
Equations in the paraxial approximation for small-scale ballooning perturbations in an axially symmetric plasma with finite pressure (β01) and the results obtained in [2] for a model magnetic field are extended in section 4.In section 5 critical beta is computed for realistic magnetic field of the gasdynamic trap.Main results are summarized in section 6.
2.Equation of ballooning modes in low-pressure plasma
In contrast to flute perturbations, ballooning modes are localized in the region of unfavorable curvature of magnetic field lines (where <0), distorting the magnetic field approximately as shown in figure 1(a), approaching zero amplitude in the region of favorable curvature(where >0).Deformation of magnetic field lines requires energy expenditure, the source of which is the internal plasma energy p/(γ −1), where p is the plasma pressure and γ is the specific heat ratio;therefore ballooning-type disturbances are unstable only at a finite value of relative plasma pressure β=8πp/B2,exceeding some limit βcrit:

The goal of exact theory is to calculate the βcritparameter, but we will restrict ourselves to simple reasoning and order of magnitude estimates.In particular,for simplicity,we assume (as it was done in [1] and many other papers) that ideally conducting ends are placed directly in the magnetic mirror throat in order to provide stability of the flute modes due to ‘line-tying’ [51, 52].Thus, we narrow the class of possible perturbations allowed to compete while minimizing the potential energy of perturbations, so the found values of βcritwill actually give an upper bound for this value.At the same time,the difference between the true values of βcritfrom this upper boundary should be small, since behind the plug there is a deep(and plasma-filled)magnetic well (a region of favorable curvature), as a result of which the magnetic field lines are actually rigidly fixed in end plugs,returning us to the condition of being frozen into the ends.
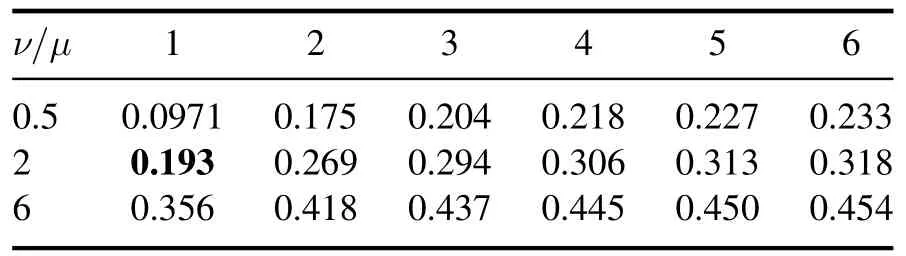
Formal theory (ignoring FLR effects) predicts that most unstable are small-scale ballooning modes with large azimuthal number m(see e.g.[7]),so that in this work we restrict ourselves to the case m ≫1.More precisely, we consider a wave package composed of many high-m modes, so that transverse shape of such package may resemble a thin knife blade as shown in figure 1(b);this assumption is not essential for further consideration and the reader may imagine a single high-m mode,periodic in azimuth angle θ.In accordance with the real situation for devices of the GDT type, we assume(following again reference [1] and many subsequent papers)that the magnetic field lines make a small angle with the magnetic axis of the system(paraxial approximation)and that the distance between the trap midplane and magnetic mirror throat L is greater than the mirror length Lmwhich should be distinguished from a quasi-uniform central part with the halflength L −Lm.The small parameter characterizing the accuracy of the paraxial approximation is a/Lm, where a is the transverse plasma size in the homogeneous part of the trap.In the paraxial approximation, integration over the field line(over dl) can be replaced by integration over the trap axis(over dz).Let us agree that the coordinates z=±L correspond to the magnetic mirrors, and the homogeneous part of the trap occupies the region|z| is obtained from the condition of constancy of the magnetic flux inside the flux tube Ψ =r02B02 =const , where r0and B0have the meaning of the radius of the flux lines and values of the magnetic field in the median plane z=0. For perturbations of the flute type in an axially symmetric mirror cell, for the projection of the displacement vector ξ normal to the field line, the following relation holds (see e.g.reference [1]): Hence, in the paraxial approximation, we find where the amplitude of the flux tube displacement ξ0=ξ0(Ψ,θ)is assumed to be a function of the magnetic flux Ψ and the azimuthal angle θ.In the case of a small-scale perturbation, the ξ0amplitude is sharply dived (localized) near some values of Ψ* and θ*, but for the time being this fact is not essential for subsequent calculations. The displacement (4) does not satisfy the condition of freezing ξn(±L)=0 at the ends which should be applied for ballooning modes, therefore instead of (4) one should consider a displacement of a more general form where α(z) is a still unknown dimensionless function.Following reference [1] we impose two boundary conditions on it: The first of them ensures the fulfillment of the condition of being frozen into the ends,and the second has the meaning of the normalization condition, it fixes the displacement at the center of the trap.Taking into account the symmetry of the problem,we assume that the sought function α(z)is even,that is,α(−z)=α(z),so it suffices to find a solution for only one half of the trap, say, for 0 As shown in[53],section 29(see also[1]),the energy of the ballooning-type perturbation is where and the prime denotes the derivative with respect to z. According to the energy principle[7],the system is stable if and only if the integral (7) is greater than zero for any function α(z) satisfying the given boundary conditions.The factor inside the first pair of parentheses in (7) is greater than zero,so the sign of WFis determined by the sign of the integral inside the second pair of parentheses.Instead of iterating over all admissible forms of the function α(z),in the problem under consideration it is possible to find a function α(z) that minimizes WF, and then determine the sign of this minimum. To find a minimum of WFfor some value of the parameter, we take the first variation of the integral (7), and set it to zero.In this way we obtain an equation that the extremal must satisfy, that is, the function α(z), which minimizes the perturbation energy WF.Since the values of the function α(z) at the ends of the integration interval are given by the boundary conditions (6), calculating the variation, we can assume that δα(0)=δα(L)=0.Taking this fact into account and integrating by parts, we get the integral which vanishes for any variation δα if A general solution of equation (10) for an arbitrary value of the parametercannot satisfy both boundary conditions (6).They are satisfied simultaneously only at some selected valueβ=βcrit. As one can see,the calculation of the critical valueβcritof the parameter, for which there is a nonzero solution to equation (10) with the above boundary conditions (6), is reduced to the quantum mechanical problem of determining the conditions for the occurrence of a zero energy level in the potential Figure 2.Ballooning mode in low-pressure plasma for amodel magnetic field profile given by equation (12); effective potential q 3q ′′is negligibly small outside a narrow region at the entrance to the magnetic mirror and therefore the eigenfunction α(z) of the Sturm-Liouville problem is well approximated probe function (13)(depicted by dashed line); particular parameters of the model are K=15, L=6, ΔL=1, Lm=2.2ΔL. It is easy to prove that the substitution of the eigenfunction and the eigenvalue in the integral (7) makes the energy of the ballooning disturbance be zero, WF=0, which corresponds to the marginal state between stability and instability.Therefore,is the marginal value of.It is evident that WF>0 if= 0.Hence, it is reasonable to expect that ballooning perturbations are stable when For the first example, let us choose the dependence of the magnetic field on the coordinate z on the trap axis in the form where K has the meaning of the mirror ratio, and 2L is the distance between the magnetic mirrors.For such a field, the effective potential function ′′q q3 is approximately equal to zero outside the plug (for 0<|z| Figure 3.Ballooning mode in the case of realistic magnetic field profile given by equation (15) for a system of two coaxial round coils.As compared to figure 2, the effective potential ′′q q3 has a wider pit, which results in higher limiting beta; parameters of the computation are K=15, L=6, b=0.6, Lm ≈3b. possessing the indicated properties, we substitute it into the integral (7) and equate the result to zero.From the resulting equation, we find the approximate value of the critical beta: For the magnetic field(12),the calculated valueβcrit= 0.580 only slightly differs from the exact eigenvalueβcrit= 0.597.The graph of the eigenfunction α(z) is shown in figure 2,where the dashed line shows the probe function α1(z). Calculations show thatβcritis very sensitive to the magnetic field profile.This fact is confirmed by the second example with the magnetic field which simulates a mirror cell composed of two coils.In this example, the critical valueβcrit= 1.18is formally greater than one, d the graph of the eigenfunction α(z) is shown in figure 3. Let us discuss the results obtained.The critical valueβcritof normalized pressure gradientβturned out to be close to one or even more than one, whereas, starting to derive the equation of ballooning oscillations in section 2, we used the approximation β ≪1 and assumed the magnetic field to be vacuum.Therefore, this hypothesis of ours was not entirely correct.At least, it fails for less steep pressure profiles, such thatβ~β0.Nevertheless,our work was not entirely useless. First of all,we note that parameterand functionΨ ),which are defined by equations(8)and(9),are not identical to the conventional plasma betawhere p0 has the meaning of the plasma pressure on its axis at Ψ=0.In a particular case when the pressure has a power-law profile for Ψ<Ψa,and p(Ψ)=0 for Ψ>Ψa,the maximum value ofis reached on the lateral plasma boundary Ψ=Ψa,whereIf k=1(pressure profile parabolic in r),the equalityholds, but for a steeper profile with k>1 the valueis greater than β0.In the same way,for a steep pressure profile close to a step, the value ofβcan be much larger than β0,so a situation is possible whereβcrit~1 whereas β0crit≪1 and the vacuum magnetic field approximation can be completely valid. The stepped pressure profile can be considered as the limit of a trapezoidal distribution close to a step with a small but finite width of the boundary layer ΔΨ.For definiteness,let us assume that the plasma pressure is equal to p0at Ψ<Ψaand decreases linearly to zero in the boundary layer with the width ΔΨ.The result of calculatingβdepends on the ratio of ΔΨ and the size δΨ of the perturbation with respect to the variable Ψ. If the size of the flute tube is small compared to the width of the border, δΨ ≪ΔΨ, the local parameter (9) in the integral (8) can be considered constant across the size of the tube, so thatwhere Ψ* is the value of Ψ on the field line,near which the disturbance is localized.Local value in the boundary layer on the field line, where the disturbance is localized,is large for a small boundary width and can easily exceed the critical value.Consequently, small-scale perturbations will be unstable even if the plasma pressure is much lower than the magnetic field pressure, i.e.β0≪1. However, small-scale oscillations are unlikely to cause great damage to the equilibrium plasma configuration.Largescale perturbations are more dangerous.If δΨ ≫ΔΨ, performing integration over Ψ in the formula(8),we can assume that Substitution of(18)into equation(8)results in the estimation There is also a second conclusion, which can be drawn from the fact established in the above, that in the approx-imation of a vacuum magnetic field it is formally Now we can assert that the critical β0in an axially symmetric mirror cell with a unsteep pressure profile is not small in comparison with unity.To correctly calculate the critical β0it is necessary to abandon the vacuum field approximation,which is also called the low-pressure approximation.The necessary calculations are relatively easy to perform for paraxial mirror traps.These are described in the next section. In the paraxial approximation, the potential energy of ballooning perturbations is found in the article by William Newcomb [3].For an axially symmetric open trap with anisotropic plasma, Newcomb gives the following expression(his formula 177) It is assumed here that the prime denotes the partial derivative with respect to z, and all functions except for Bvac=Bvac(z),X=X(θ, Ψ, z), and Y=Y(θ, Ψ, z), depend on Ψ and z,p‖and p⊥are the parallel and transversal components of the plasma pressure tensoris the unit tensor and h is the unit vector parallel to the magnetic field.Newcomb pointed out that the function Q is positive under the condition of stabilization of the firehose instability which was always assumed to be fulfilled.Otherwise,the first term in square brackets in the integrand (20) becomes negative (destabilizing), like the second term. Minimizing WFover Y gives ′′ =Y0,which allows us to consider the term with ′Y2in(20)as zero.The calculations for this case were performed by Bushkova and Mirnov [2].They investigated the limit of isotropic plasma, when p⊥=p‖=p(ψ) and rewrote equation (20) in the dimensionless form convenient for numerical calculations: where ψ=Ψ/Ψa, Varying the integral (23) leads to the equation The same equation can be deduced from equation (18) in [6]if we put zero frequency,ω=0.Calculations were performed for the pressure profile Table 1.Critical beta for local perturbations on the extreme field line ψ=1 for biquadratic pressure profile f(ψ)=1 −ψ2, mirror ratio K=100, and various values of the parameters μ and ν.Our calculations basically confirm the results of[2]with small deviations in the case of large values of the parameters μ and ν. Table 2.Same as in table 1 for more unsteep quadratic radial pressure profile f(ψ)=1 −ψ not analyzed in [2]. which is biquadratic in radius r(in case of low beta);it allows one to calculate the integral (24d) and write in analytic form the equation of the field line: The critical beta was calculated for the boundary field line at ψ=0.99 for a family of axial profiles of the vacuum magnetic field with mirror ratio K=100 and a set of parameters μ and ν.In order to check our code,we recalculate their results assuming the boundary conditions and obtained similar results,which are listed in table 1.In our numerical code, we implemented some sort of shooting method.In particular, we used Wolfram Mathematica© and its built-in function ParametricNDSolve to solve equation(25)with boundary conditions X=0 and dX/dz=0 at z=0 with β0as free parameter, and then used another built-in function FindRoot to find a root of the equation X(L)=0. The performed calculations show that the profile (28)with parameters μ=1, ν=2 becomes unstable with respect to ballooning vibrations at β0>0.366.This profile is of particular importance because it provides the best conditions for stabilizing the flute instability.It can be shown that this profile minimizes the destabilizing contribution of the central section to the Rosenbluth-Longmire criterion of flute stability [54]. Figure 4.Critical beta versus parameter μ in case of ν=2 for three radial profiles of the plasma pressure. Table 3.Same as in table 1 for more sharp radial plasma profile f(ψ)=1 −ψ4 not analyzed in [2]. To increase the critical value βcrit,Bushkova and Mirnov proposed to go to steeper axial profiles of the magnetic field described by equation(28)with μ,ν ≈5 −6.In this way,one can raise βcritto the values above 0.7.It is this value that was indicated in the final section of their paper [2] and was mentioned in later publications as one of the main characteristics of the superiority of open traps over tokamaks.However, such a large limiting beta was obtained for unrealistic magnetic field axial profiles with very short (‘point’)magnetic mirrors.The limiting value of beta, calculated for the model field equation (28) with μ=1, ν=2, approximately implemented in the GDT, was exceeded in the experiments on this facility by almost 2 times [41]. We have already seen in section 3 that the critical beta is larger for unsteeper pressure profiles.It is not entirely clear why Bushkova and Mirnov, like other authors of those years(see e.g.[22]), limited themselves to the analysis of the biquadratic pressure profile, which is described by the function f(ψ)=1 −ψ2.Perhaps the only reason was the fact that for this radial profile, some of the calculations can be done analytically.Figure 4 illustrates the effect of plasma pressure profile on critical beta by presenting its dependence on the parameter μ for the case ν=2. To study the effect of the radial plasma pressure profile,we calculated the critical beta values for a unsteeper pressure profile,described by the function f(ψ)=1 −ψ,and a steeper pressure profile, described by f(ψ)=1 −ψ4, with the same set of parameters μ and ν as in table 1.The calculation results are presented respectively in tables 2 and 3.As would be expected from the discussion in section 3,the unsteep plasma pressure profile is more robust against small-scale ballooningdisturbances.The calculation for a parabolic radial pressure profile (table 2) gave very high values of beta approaching unity.These values are obtained for large parameters μ and ν.They correspond to the axial profile of the magnetic field that grows very steeply near the magnetic mirror, which can hardly be formed in a real mirror trap.We made the calculation for such values of μ and ν just to compare our results with the results of [2]. Table 4.Critical values βcrit of the normalized pressure gradient,calculated in the low-pressure plasma approximation by the method described in section 2.This data should be compared with the data in table 2. Table 5.Critical beta for local perturbations on the extreme field line ψ=1 for three radial pressure profiles f(ψ) and three positions zend of plasma limiter or receiver. We have also added table 4 with the critical valuesβcritof the normalized pressure gradient (8) in the low-pressure plasma approximation,as described in section 2.These values are best compared with the data in table 2, since the value of the function (9) on the boundary field line coincides with β0for this particular table.The comparison shows that the lowpressure plasma approximation overestimates the critical value β0critfrom one and a half to two and a half times in the case of the magnetic field with an axial profile of the form (28). The vacuum magnetic field in the GDT facility operating in the Budker institute is symmetric about the equatorial plane z=0 [55, 56].Figure 5 shows the axial profile of the magnetic field in one half of the GDT for two options for switching magnetic coils:the so-called standard version of the GDT and the GDT with a short pit (short mirror cell).In the second variant,a shallow local minimum of the magnetic field is formed near the stopping point of fast ions (z ≈140 cm).For comparison, dashed line depicts model field discussed in previous section 4 and given by equation (28) with parameters μ=1 and ν=2. Figure 5.Axial profile of vacuum magnetic field in gas-dynamic trap.Dotted line depicts model magnetic field given by equation(28)with parameters ν=2, μ=1, K=31.7;note that equation (28) is not applicable to the expander region z>L=350 cm. A population of fast ions arises in the GDT upon oblique injection of beams of neutral atoms at the angle of 45°to the axis of the trap.Due to the presence of fast ions, the plasma pressure in the GDT is anisotropic, i.e.p⊥≠p‖, and the function p⊥depends not only on the magnetic flux ψ,but also on the magnitude of the magnetic field B.In the central section of the GDT (i.e., between the magnetic mirrors), function p⊥(ψ, B) has a maximum near the stopping point of fast ions,and in the expander (i.e., outside the central section) it decreases roughly proportional to B.As a result of all this, it turns out that equation(21b)cannot be solved analytically for B and r, as in the case of an isotropic plasma.Thus, calculating the critical beta in anisotropic plasma requires much more complex calculations than the method described in section 4 allows.To simplify our task, we ignore the fact of anisotropy and still use the method from section 4,taking into account that the plasma pressure varies only slightly along the magnetic field lines in the region|z|≤400 cm,where the magnetic field is not less than in the middle of the central section at z=0 cm. Since the axial profile of the magnetic field along the GDT axis is rigidly set by the configuration of the magnetic system,the only free parameter that can affect the critical beta is the coordinate zendof an imaginary or real conducting plasma diaphragm, on which the perturbation X vanishes.In other words, we calculated the limit for beta by solving equation (25) with the boundary conditions The results of calculations are presented in table 5 for two magnetic field configurations and three values of zend.The coordinate zend=400 cm corresponds to the placement of the plasma receiver in the expander,and zend=350 cm in the magnetic plug.Finally, zend=329.5 cm marks the coordinate of an actually existing conducting diaphragm, which is actually capable of playing the role of a line-tying stabilizer of small-scale flute disturbances on the lateral surface of the plasma column.Analysis of the data in the table shows that there is a very strong dependence of the critical value of beta on the steepness of the radial plasma pressure profile, but the dependence on the coordinate zenddoes not seem to be very significant.The second point to pay attention to is a noticeable decrease in critical beta in a GDT configuration with a short pit compared to the standard version of GDT.This is the expected result. Figure 6.Axial profile of the vacuum magnetic field curvature in gas-dynamic trap along a field line that has unit radius at z=0. On the other hand, comparison of the calculation results in table 5 for zend=350 cm (they are in bold) with the calculation results for the model field(28)leads to an unexpected conclusion.As it was mentioned in section 4, the magnetic field in the GDT was designed to minimize the destabilizing contribution of the central section to flute modes.Such a minimum is provided by equation (28) with parameters μ=1 and ν=2.The corresponding critical beta values in tables 1–3 are shown in bold.Due to the discrete structure of the magnetic system, the real magnetic field in the GDT is slightly rippled and only approximately follows the formula(28).However the ripples are not visible on the plot of the magnetic field strength,so that figure 5 might give an impression that the model function (28) quite well approximates actual magnetic field in the GDT.This is not completely true as is clearly seen in figure 6, which shows that the curvature of the magnetic field line oscillates and strongly deviates from smooth curvatures computed from equation (28).The curvature ripple can be expected to lead to a significant change in the critical beta,but according to table 5, the critical beta turned out to be only slightly higher than in the tables 1–3. The real radial profile of the plasma pressure in the GDT facility does not coincide with any of the theoretically investigated power-law profiles, but it is closer to a unsteep profile than to a stepwise one.The result of measuring the diamagnetic weakening of the magnetic field near the stopping point of fast ions are shown in figure 7.The measurements were carried out using a motional Stark effect (MSE) diagnostics [57].The diagnostics is located in the position with a local mirror ratio R=2 (in the vacuum magnetic field), and the transverse coordinate x in the figure is local to this position (that is, it is not a projection into the central plane of the GDT in terms of the magnetic flux).The diagnostics uses a deuterium beam with the energy of 50 keV,and the measurements were made at the moment of time 7.5 ms from the start of the plasma shot with an exposure duration (time integral) 1 ms. According to the data of diamagnetic probe near the stopping point, the total energy of the population of fast deuterium atoms was approximately 2 kJ.The experiment clearly observed the effect of ‘pinching’ the beta profile, the flux of chargeexchange atoms(i.e.,the density of fast ions)and the flux of the D-D reaction products.The maximum value of ΔB/Bvacin figure 7 is 0.304±0.017, which corresponds to the maximum betaβ0= 2(ΔBBvac) − (ΔBBvac)2= 0.516 ±0.036. As can be seen from the figure,the radial plasma pressure profile does not have a clearly defined boundary within the measured range.The relatively narrow peak in the center is due to the effect of pinching of fast ions, the reasons for which are not fully understood [58].The peak width is comparable to the Larmor radius of fast ions;therefore,in this part, the pressure profile should be stable against small-scale perturbations due to FLR effect.As for the periphery of the pressure profile, it should be stable at the indicated values of beta,since here the pressure gradient is obviously less than at the edge of the parabolic profile at the same plasma diameter. In the case when plasma column has no strictly defined boundary (as the profile given by equation(16) has at Ψ=Ψa) and is surrounded by a halo, one could try to compute critical beta for a perturbation localized on any of the internal field lines and choose minimal one.However ballooning instability localized inside plasma column might not be disastrous for plasma confinement (this is an idea behind the so called vortex confinement in mirror traps proposed by Alexey Beklemishev [59]).This means that there is no simplified formulation of the problem of calculating critical beta for a plasma column with a halo. We have shown that steepening of the radial plasma pressure profile leads to a decrease in the critical value of beta, above which small-scale balloon-type disturbances in a mirror trap become unstable.We may therefore expect that small-scale ballooning instability leads to ‘unsteepening’ of the radial plasma profile provided, of course, that the FLR effects on MHD stability are negligible.This conjecture has probably not been properly emphasized and appreciated in earlier publications.It is known that the study of the stability of the global ballooning mode leads to the opposite conclusion on some occasions.For example, reference [30] states that wall stabilization of the global ballooning mode is more effective for plasma with a hollow pressure profile.Key words here are wall stabilization which works better in the case when plasma profile exibits sharp gradients near the lateral wall of the conducting vacuum chamber. We also calculated the critical beta values for a realistic magnetic field in two configurations of GDT:the standard GDT and the GDT with short pit.For the version of the standard GDT,the calculation result practically coincided with the results of Bushkova and Mirnov[2].They modeled the axial profile of the magnetic field by a smooth function (28) with parameters μ=1 and ν=2,and described the radial profile of the plasma pressure by a biquadratic polynomial.However,the value 0.359 of limiting beta calculated by them turned out to be almost two times less than the value of 0.6, achieved later in experiments on the GDT [40].Our calculations for other pressure profiles showed that at best the critical beta is 0.719,i.e.slightly exceeds the value achieved in the experiment. In addition, our calculations showed that the approximation of the axial magnetic field in the GDT by smooth functions gives a very accurate prediction for the limiting beta value.This fact was not expected in advance, since the real magnetic field in the GDT has significant ripples. Strictly speaking, the coincidence of the critical beta calculated by us with the experimental data may turn out to be accidental, since we ignored the FLR effects.Unfortunately,quantitative comparison of experimental data and predictions of FLR theory has never been done.Plasma in the GDT is essentially two-component.Relatively cold (target) plasma ions have a relatively low temperature at the level of several tens of electronvolts.For the target plasma, the parameter a2/ρiL,which characterizes the boundary value of the number m, is much greater than 1.Fast ions of the hot plasma component have an energy of more than 10 keV.For them,the parameter a2/ρiL is less than one.In other words, for the cold plasma component, the FLR effects are insignificant up to comparatively large values of the azimuthal number m,while for the hot plasma component they stabilize modes with all values of m, except for m=1.Some results of numerical calculations taking into account the effects of FLR in onecomponent plasma with biquadratic pressure profile are presented in[10,22].These calculations confirm the need to take into account the effects of FLR, which should be done in a future article. Acknowledgments The work was financially supported by the Ministry of Education and Science of the Russian Federation.This study was also supported by Chinese Academy of Sciences Presidents International Fellowship Initiative (PIFI) under Grant No.2022VMA0007 and Chinese Academy of Sciences International Partnership Program under Grant No.116134KYSB20200001. The authors are grateful to Vladimir Mirnov for valuable explanations of the method he used to solve equation (25),and to Dmitry Yakovlev for providing the results of calculating the magnetic field in the GDT. ORCID iDs







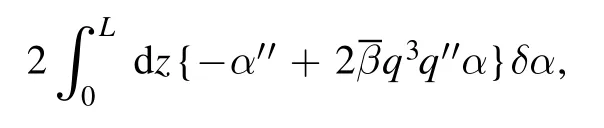

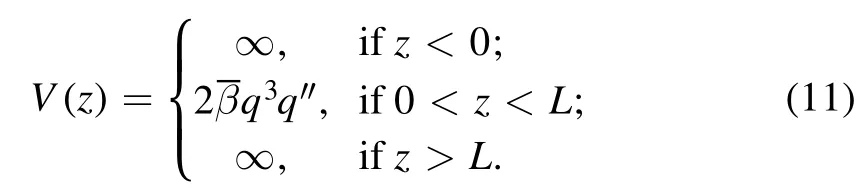

3.Critical beta in low pressure plasma






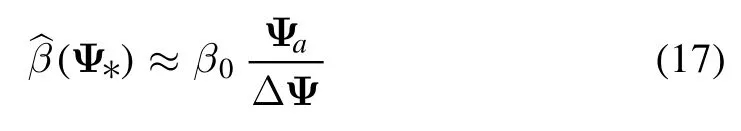


4.Paraxial mirror trap


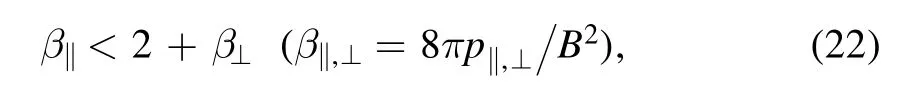












5.Gas-dynamic trap



6.Summary
 Plasma Science and Technology2022年1期
Plasma Science and Technology2022年1期
