基于脉冲注入理论的页岩储层微破裂试井解释技术及应用
王妍妍,王卫红,胡小虎,刘 华,蒋晓蓉,戴 城,方思冬
(1. 页岩油气富集机理与有效开发国家重点实验室,北京 100083; 2. 中国石化石油勘探开发研究院,北京 100083;3. 成都理工大学能源学院,四川 成都 610059)
微破裂测试是在正式压裂作业之前开展的注入或衰减试验,通过注入少量流体在井筒附近产生微小裂缝,分析压力衰减数据获取相关参数[1]。微裂缝最初用来评价压裂设计所需参数[2-3],但裂缝闭合后若继续监测压力衰减,则可用后期数据推算地层压力和压前渗透率等参数[4-5]。与常规的关井压力恢复试井类似,微破裂测试分析也是利用关井压力数据反演参数,但微破裂测试中,裂缝随压裂液的驱动实时产生并逐渐闭合[6],而常规关井压力恢复中裂缝或其他储层特征预先存在[7-9]。因此需要一种特殊的微破裂解释手段。
目前微破裂解释模型有两类。第一类模型:假设裂缝动态扩展时沿着裂缝壁面分布的注入源在地层中产生压力响应,利用点源函数建立压力动态正演模型[10]。但这类模型应用前需要已知液体滤失和裂缝扩展两个子模型,而这难以提前预知或反演得出。第二类模型:根据微注入后地层中可能出现的流态,将裂缝扩展简化成裂缝预先存在,以及裂缝闭合简化为裂缝并不存在,建立具有一定导流能力的垂直压裂直井模型[11]或者直井模型[12]来分别刻画早期和晚期压力动态。第二类模型因可操作性在实际应用中更为广泛。以第二类模型为基础,形成了两种储层参数解释方法:一种是压力恢复试井分析中的导数曲线分析法[13];另一种是特种曲线分析法,其包括关井后期拟径向流直线分析方法[10]、Horner 特种直线分析法[14]和Notle 特种直线分析法[15]等。导数曲线、拟径向流直线、Horner 特种直线等分析法均需要一定开井时间保证解释精度,而微破裂测试过程中生产(注入)时间极短。Notle 特种直线分析法是在假设油(气)井定压生产(注入)基础上建立的,而实际过程更加类似于定产生产(注入)。因此,这些方法在微破裂试井分析中存在不适应性。
本研究提出了一种新的微破裂试井模型及参数解释方法,解决了常规关井压力恢复试井分析方法不适用于“短注入期、长衰减期”问题。新的模型将开、关井看作整体,假设压力响应是注入期和关井期压力响应的总和,在此基础上建立微破裂试井解释模型。根据模型的渐进解释引入了3 条组合诊断曲线,并建立了主控流态识别+特种直线分析的微破裂试井解释方法和流程,很大程度上提高了参数解释精度,利用该方法对涪陵页岩气田南川区块两口测试井进行了分析解释,验证了方法的实用性。为现场实测微破裂数据的分析解释提供了有效手段,也为页岩储层评价和选区[16-18]提供了关键的指标参数[19-21]。
1 微破裂试井解释模型
1.1 微破裂测试曲线
微破裂测试时向地层注入少量流体然后关井,关井之后(包括注入过程中)流体逐渐滤失进入地层,同时压力开始往外波及。这一测试过程获得的压力及产量历史曲线如图1 所示,图中产量为负值,表明该过程是流体注入。曲线包含3 个阶段:①压裂液注入期;②压裂裂缝关闭期(从地面泵送停止开始到压开的裂缝关闭结束);③压裂裂缝关闭后期。第3 阶段反映裂缝及井筒附近地层特征,通过该阶段的数据可以获取裂缝及地层的相关参数,如原始地层压力和原始渗透率,本研究主要针对这一阶段。
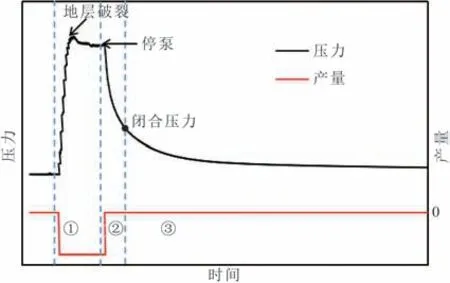
图1 微破裂测试过程中产量-压力曲线示意图Fig.1 Sketch map of production variation with pressure curve during a mini⁃frac test
测试时裂缝的扩展和闭合过程如图2 所示。横轴表示裂缝长度x,纵轴表示时间t,且以地层破裂开始时刻作为零点。t=0 时裂缝长度为零,tinj时刻泵注结束(关井),之后裂缝将继续延伸并达到最大值xfmax,然后开始闭合,最终在裂缝闭合时刻tc处完全闭合。此时裂缝内流体全部滤失到地层中。在确定原始状况下的地层参数时,多关注停泵后的压力响应。
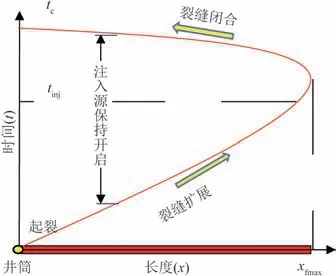
图2 裂缝扩展及闭合过程示意图Fig.2 Sketch map of fracture propagation and closure
1.2 注入流体性质的影响
在利用停泵后的压力响应反演储层参数时,需要用到储层流体性质参数。页岩气微破裂试井分析与常规关井压力恢复试井分析还存在一点不同,即注入流体往往是压裂液,而储层流体是天然气,二者物性差别大,地层中存在两相流动。因此,在微破裂试井解释中,要考虑主控流体的物性,进行数据的分析诊断。
目前普遍认为[22]近井附近裂缝中两相流现象更为明显,而在线性流及后期拟径向流阶段,压力波及范围内含气饱和度较高,此时天然气的高压缩性导致其在压力瞬变过程中起主导作用。
1.3 基于脉冲注入的渗流数学模型
经典的不稳定压力分析方法多针对关井压力恢复测试提出,将压力恢复过程视为两部分,即开井压力降落及关井压力恢复,并利用叠加原理模拟气井生产一段时间后再关井的压力恢复响应。微破裂测试过程中,注入(开井)时间很短,与关井时间相比,可以近似为一个脉冲信号,本研究的微破裂试井模型在处理“短注入期、长衰减期”问题时,将脉冲注入和关井看成一体,早期注入和关井的影响在渗流数学模型的内边界条件处加以考虑。
1.3.1 模型假设及无因次参数
建立渗流数学模型时做如下假设:①气井位于无限大储层中;②储层及流体微可压缩;③忽略重力效应,把地层流动看成二维流动;④考虑表皮和井筒储存效应。
无因次参数定义为:
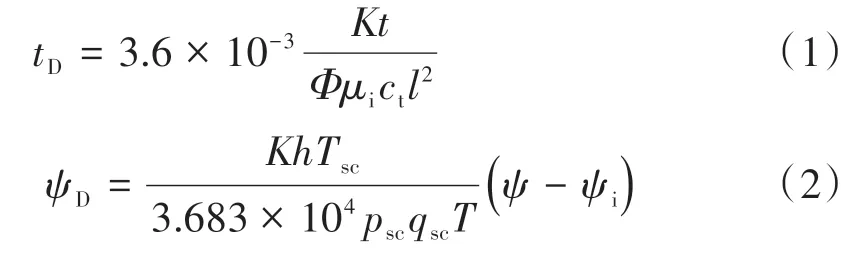
式中:K为渗透率,10-3μm2;t为总时间,h;Φ为孔隙度,小数;μ为粘度,mPa·s;ct为综合压缩系数,MPa-1;l为长度,m;h为厚度,m;T为温度,K;p为压力,MPa;q为气产量,104m3/d;ψ为拟压力,MPa2·mPa-1·s-1。下标D为无因次;下标i为原始状态;下标sc为标准状态。
另外,需要注意该无因次参数定义中,注入开始时刻作为时间起始点,即t=tinj+△t(△t为关井后时间,h;下标inj 为开井注入过程)。而且对于气藏,虽然注入流体为水(或压裂液),但在对于最常见且对解释参数最有用的流动阶段,如拟径向流等,流体物性参数要选择气体参数,故此处使用拟压力进行分析;l为参考长度,对于注入源几何形状为裂缝,以及地层中为线性流的情况,参考长度(l)为裂缝半长(xf),关井后期注入源几何形状影响可以忽略(关于这一点Notle等人曾在脉冲压裂渗流数学模型中专门论述过,此处不再进行赘述),压力扩散模式接近瞬时点源产生的拟径向流,此时参考长度(l)为井半径(rw)。
若想获取储层参数,需要着重分析压裂裂缝关闭后期测试数据。通常可将这段历史分成两个阶段:早期的线性流和后期的拟径向流。通过分析线性流阶段数据,可以获取裂缝半长,也可以初步判定原始地层压力;而分析拟径向流阶段数据则可较准确评价地层原始压力和渗透率。因此,接下来重点针对这两个阶段分别建立渗流数学模型,并进行求解和分析。
1.3.2 拟径向流模型
拟径向流动阶段是微破裂解释时最重要的流动阶段,该阶段的数据可以用来准确确定储层参数,因此是否录取到该阶段的测试信息一定程度上代表了此次测试的成功与否。根据拟径向流动阶段特征,建立拟径向流模型:
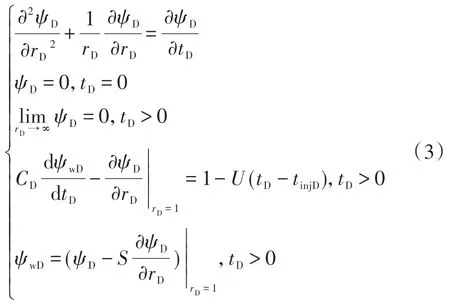
式中:S为表皮系数,无因次;C为井储系数,m3·MPa-1;r为距离,m。下标w为井底位置处。
模型内边界条件处引入了阶跃函数U(z)来考虑短暂注入的影响。U(z)定义为:
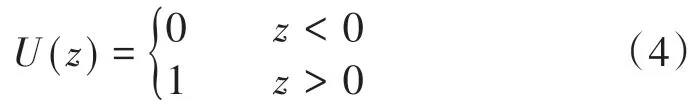
式中:z为一般变量,无因次。
对上述数学模型进行Laplace变换,并令:
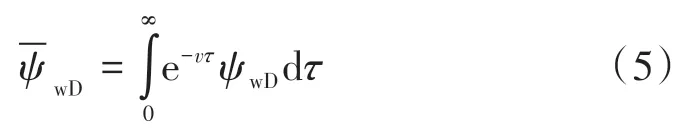
式中:v为拉普拉斯变量,无因次;τ为时间,h。变换后的渗流数学模型结合Bessel 方程进行求解,可得模型在Laplace空间中的解为:
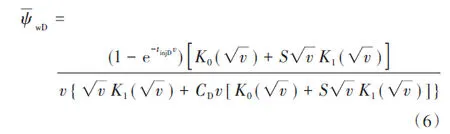
式中:tinjD为生产时间,无因次;K0为0 阶Bessel 函数;K1为1阶Bessel函数。
通过Stehfest数值反演算法[23]可将上述模型的La⁃place 空间解转化为实空间的数值解。在双对数坐标曲线中绘制ψwD-tD关系曲线如图3所示。
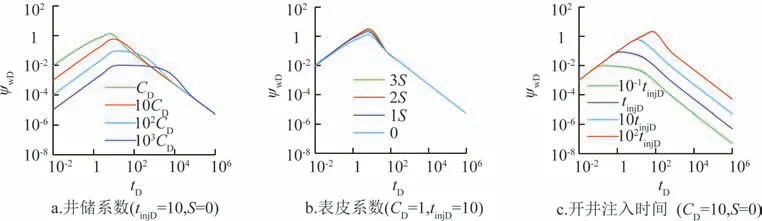
图3 不同参数对拟径向流阶段压力动态曲线的影响Fig.3 Influence of different parameters on dynamic pressure curve for pseudo⁃radical flow regime
图3 显示了井储系数、表皮系数和开井注入时间对井底压力的影响。曲线早期受井筒存储效应影响,表现为斜率为1 的直线;之后经历过渡段(驼峰),后期真正进入拟径向流动阶段后曲线表现为-1 斜率直线。井筒储存及表皮效应的存在使得-1 斜率直线段延迟出现,而注入时间决定了-1 斜率直线段截距,注入时间越长,-1斜率直线段截距值越大。
1.3.3 线性流模型
若地层中出现拟径向流动,可认为产生的裂缝已完全关闭。在页岩储层中,由于地层渗透率低,当微破裂作业的注入停止后,在一定时间内裂缝仍不能关闭,此时裂缝中将会出现线性流。假设流体流动严格遵循线性模式,若同时考虑井眼、井身和表皮的影响,并在内边界条件处考虑短暂生产的影响,可建立线性流动阶段渗流数学模型:
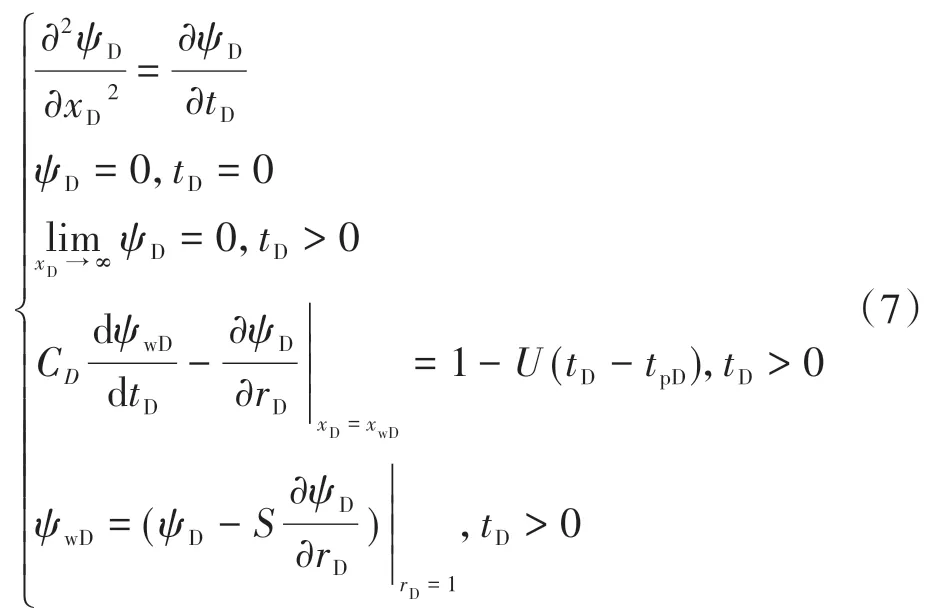
式中:x为裂缝长度,m。
与拟径向流模型求解方法类似得到:
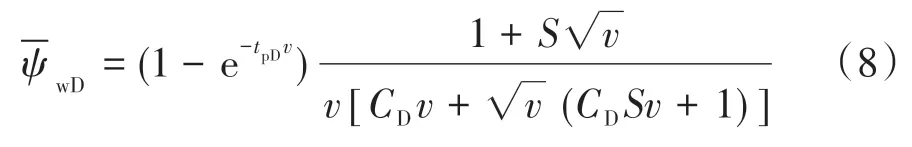
在双对数坐标曲线中绘制ψwD-tD关系曲线如图4所示。
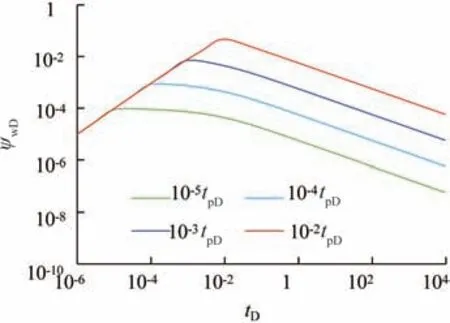
图4 生产时间tpD对线性流阶段压力动态曲线影响(S=0,CD=0.1)Fig.4 Influence of different producing time(tpD)on pressure dynamic curve for linear flow regime(S=0,CD=0.1)
曲线早期特征也受井筒存储效应和表皮系数影响,这和拟径向流类似,区别在于后期进入线性流动阶段后曲线表现为-1/2 斜率直线,且直线截距大小受无因次注入时间影响。
2 诊断分析及参数解释方法
2.1 不同流动阶段渐进解
上述模型的解较复杂,但可通过渐进分析得到近似解。对于拟径向流模型的解公式(6),在经历足够长时间的关井后,井筒储存的影响应减小。v减小,分母中含有CD的第二项的影响可以忽略不计,表皮效应也与之类似,进而推出经历较长关井时间后无因次拟压力在Laplace空间的渐近解为:
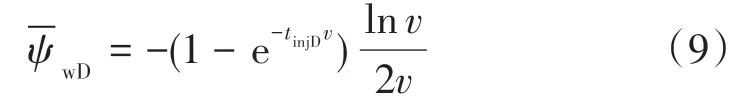
其中指数项可以进行泰勒展开,得到:
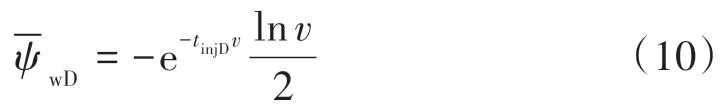
上式进行Laplace反变换可得:

同样的方式,可以得到线性流动阶段无因次拟压力的在Laplace空间、真实空间中的渐进解分别为:

将上述无因次渐进解有因次化之后得到对应流动阶段拟压力表达式,其中拟径向流动阶段为:
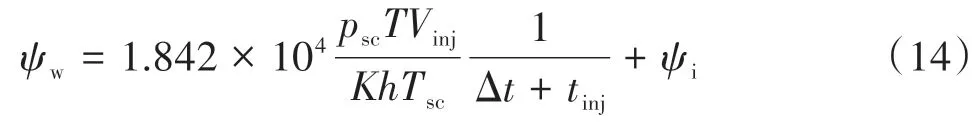
式中:Vinj为滤失进入地层中的流体体积,m3。
线性流动阶段为:
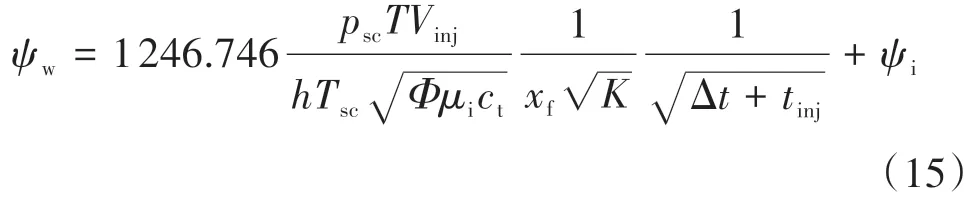
2.2 诊断曲线1
根据公式(14)和公式(15),若以ψw-ψi为纵坐标,以Δt+tp为横坐标,分别取对数,对于拟径向流阶段有:
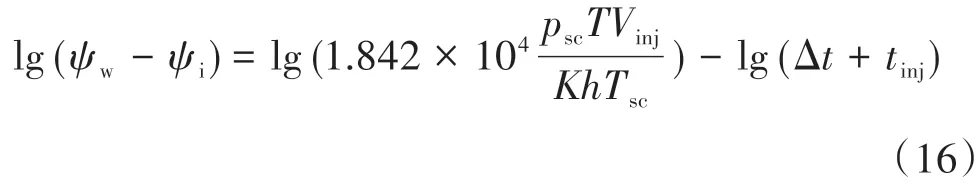
对于线性流动阶段有:
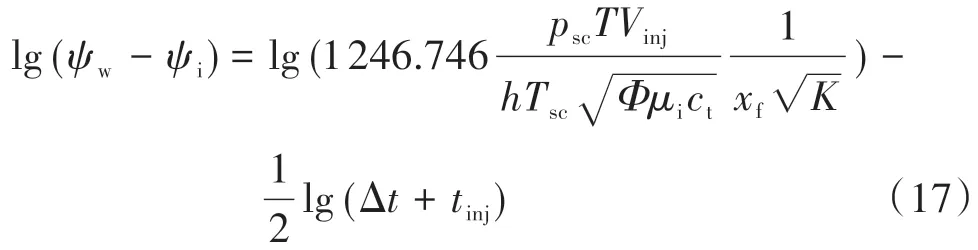
即拟径向流动和线性流动阶段,(ψw-ψi)-(Δt+tp)曲线在双对数坐标中将分别出现-1和-1/2斜率直线段。因此可以将(ψw-ψi)-(Δt+tp)双对数曲线作为诊断曲线1,并根据-1 和-1/2 两个特征斜率段识别对应的流动阶段。
需要注意的是此处用到的双对数曲线与常规关井压力恢复试井分析用到的双对数曲线有很大不同,表现为横坐标是Δt+tinj,纵坐标是Δψw。而非关井压力恢复试井分析中用到的Δt,ψw-ψ(tinj)。这也意味着绘制诊断曲线1 需要已知原始地层压力,而微破裂解释过程中原始地层压力为待解释参数,可以采用试凑法进行分析,但这种方法相对繁琐,因此引入新的诊断曲线解决该问题。
2.3 改进的诊断曲线分析方法
在公式(14)和公式(15)的基础上求拟压力的半对数导数及其与时间的乘积,分别记为ψw′和ψw′′。另外考虑到注入流体后再关井地层压力会逐渐下降而非升高,求导数时引入负号。对于拟径向流阶段有:
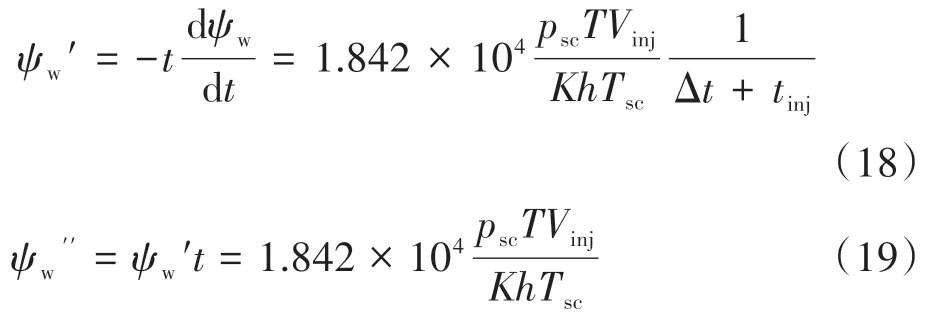
从公式(18)和公式(19)中可以看出,在ψw′ -t、-t双对数图中,即便ψi不确定,曲线仍然呈现出-1 和0 两个特征斜率,因此可以借助这两条曲线来识别拟径向流,并将其作为诊断曲线2和诊断曲线3。
根据建立的渗流数学模型,计算得到3 种诊断曲线如图5所示,模型的基础参数见表1。从图中可以看出,拟径向流动阶段3种诊断曲线分别将呈现明显的-1,-1及0斜率。
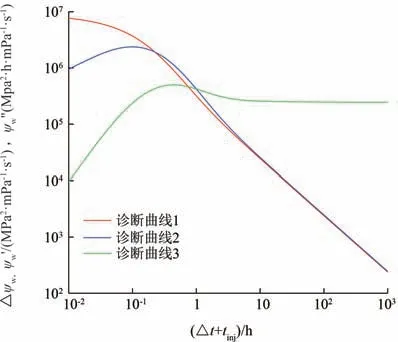
图5 拟径向流阶段组合诊断曲线Fig.5 Combined diagnosis curve for pseudo⁃radical flow regime
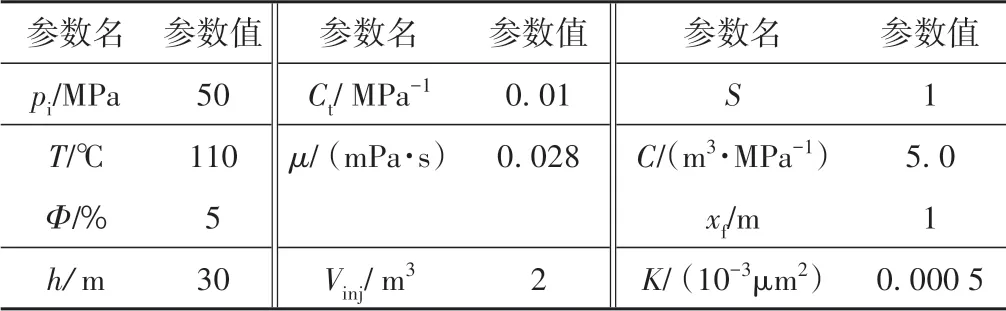
表1 算例模型基础参数Table.1 Basic parameters used in the mathematical diffusion⁃filtration model
识别出拟径向流动阶段后,可提取该阶段的数据,并绘制ψw-t-1特种直线,根据特种直线斜率mR结合公式(14)可以求取地层渗透率:
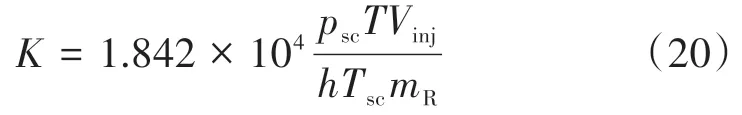
式中:mR为拟径向流阶段特种直线的斜率,MPa2·mPa-1·s-1·h。
此外,从公式(14)中可以看出,当关井时间△t足够长时,趋于0,此时关井压力pws趋于pi。因此在ψw-t-1特种曲线上,将直线段延长,让其与0相交,交点对应的压力称为外推压力,对于尚未投入开发的气藏,该值就是原始地层压力(图6)。
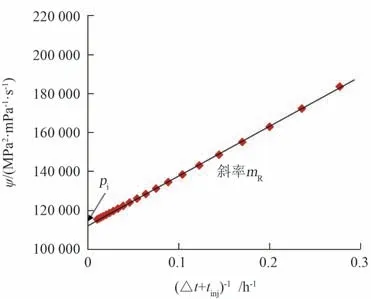
图6 拟径向流阶段特种直线Fig.6 Special straight line for pseudo⁃radical flow regime
若绘制诊断曲线1 时,原始地层压力选择不正确,则曲线将偏离-1 斜率段(图7)。因此分析时,首先依靠诊断曲线2 和诊断曲线3 进行诊断,并根据诊断结果绘制特种曲线求取原始地层压力和渗透率。地层压力求取完成之后,再绘制诊断曲线1,若此时诊断曲线1 和诊断曲线2 重合,则证明原始地层压力计算正确,否则需进一步微调该参数,直至两个曲线重合到-1斜率直线上。
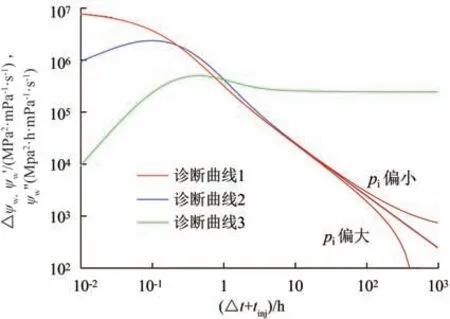
图7 原始地层压力对拟径向流阶段压力动态曲线影响Fig.7 Influence of initial pressure on dynamic pressure curve for pseudo⁃radical flow regime
同样地,对于在线性流动阶段拟压力解的基础上计算诊断曲线2和诊断曲线3,有:
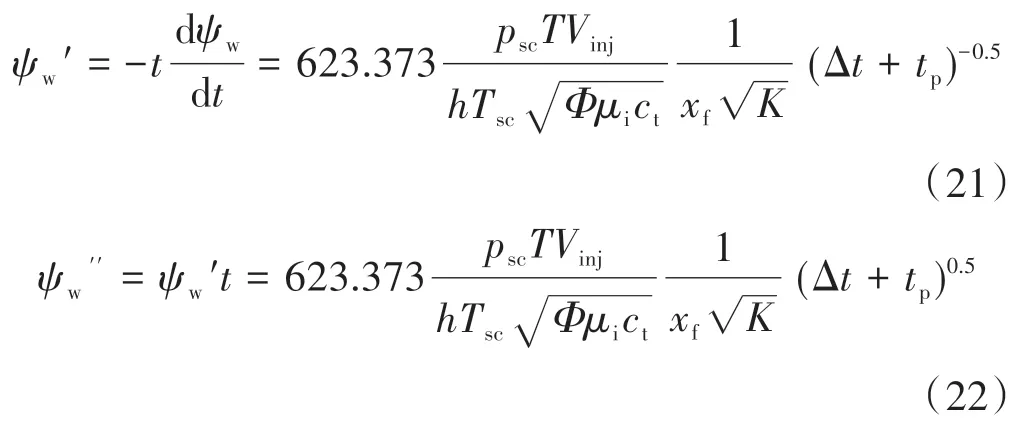
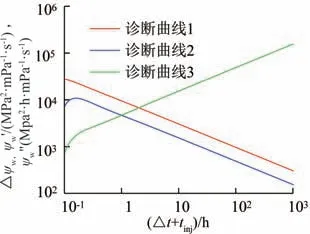
图8 线向流阶段组合诊断曲线Fig.8 Combined diagnosis curve for linear flow regime
根据公式(15),识别出线性流动阶段后,可提取该阶段的数据,并绘制特种曲线,根据特种曲线斜率结合拟径向流分析求得的渗透率可得到裂缝半长:
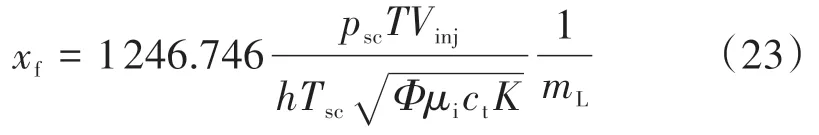
式中:mL为拟径向流阶段特种直线的斜率,MPa2·mPa-1·s-1·h0.5。
此外,从公式(23)可以看出,将特种曲线上直线段延长,让其与=0相交,交点对应的压力也为原始地层压力(图9)。
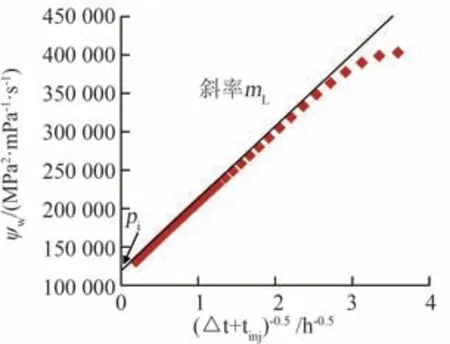
图9 线向流阶段特种直线Fig.9 Special straight line for linear flow regime
进一步地,与拟径向流分析类似,若原始地层压力求取完成之后,可重新绘制诊断曲线1,此时,诊断曲线1 的截距为诊断曲线2 截距的2 倍,且二者平行,否则可证明求取的原始地层压力不正确(图10),需要重新进一步修正以获得最终正确的取值。
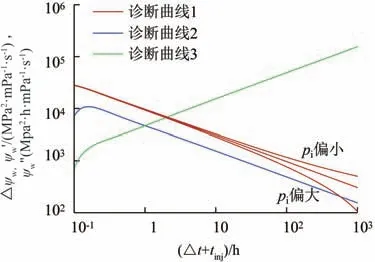
图10 原始地层压力对线性流阶段压力动态曲线影响Fig.10 Influence of initial pressure on dynamic pressure curve for linear flow regime
3 解释流程
不同流动阶段的压力解及诊断曲线斜率汇总表如表2所示。

表2 不同流动阶段压力解及诊断曲线斜率Table 2 Pressure solution and slope of the diagnosis curve for different flow regimes
根据上表结合上述分析过程,可以得到微破裂试井解释流程。现场实测数据分析时,可先初步绘制诊断曲线1,但重点关注诊断曲线2 和诊断曲线3,用其定位特殊斜率段,结合流态识别结果选取合适特种直线,计算原始地层压力和渗透率等参数,最后利用3个曲线进一步确认解释结果。解释流程如图11所示。
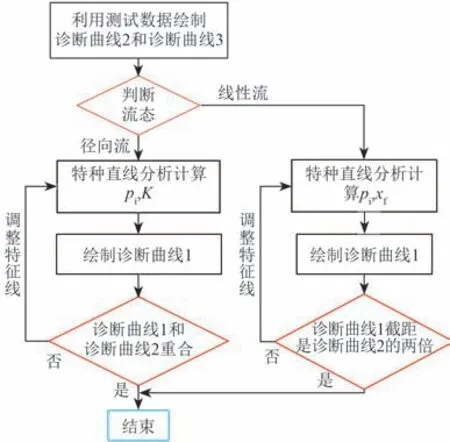
图11 分析方法流程Fig.11 Flow chart of the proposed analysis method
4 实例分析
涪陵页岩气田南川区平桥背斜南部气井A-1井和A-3井开展了微破裂测试,其中A-1井位于背斜西侧,A-3井位于东侧且靠近断层。为认识储层物性[24]并分析断层对保存条件的影响[25-26],在压裂之前开展了测试。测试参数如表3所示。

表3 涪陵页岩气田实例井泵注参数Table.3 Basic injection parameters for the case study of Fuling shale gas field
两口井均录取到拟径向流。以A-3 井为例,通过诊断曲线2 和诊断曲线3 分析确定拟径向流出现的时间,如图12a所示,提取该段数据画特种曲线,如图12b所示,可以求得原始地层压力为45.29 MPa,压前渗透率为0.000 21×10-3μm2,之后重新绘制诊断曲线1,此时诊断曲线1和3重合,证明计算结果合理。若原始地层压力认识有误(如44.00 MPa),诊断曲线1将偏离诊断曲线2,如图12c所示。
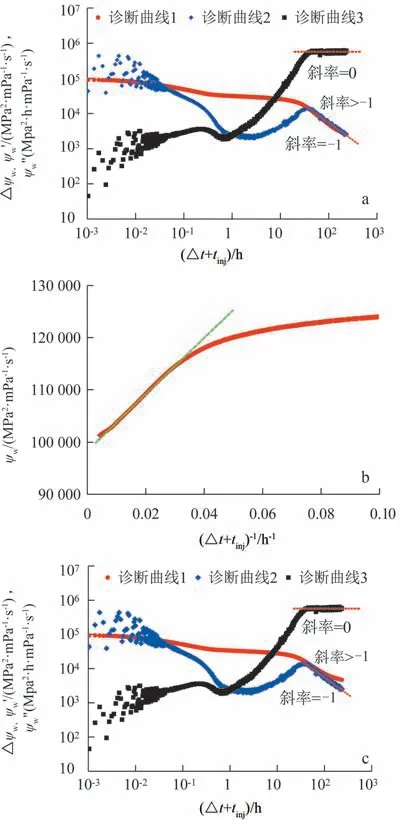
图12 涪陵页岩气田A-3井拟径向流分析结果Fig.12 Results of pseudo⁃radial regime analysis for Well A⁃3 in Fuling shale gas field
对于A-1井,拟径向流的分析与A-3井类似,最终评价得到压前渗透率为0.000 053 1×10-3μm2,地层压力为45.41 MPa。该井也录取到了线性流,根据诊断曲线,如图13a 所示,截取线性流阶段数据,绘制特种直线,如图13b 所示,计算得到此次微破裂测试形成的裂缝半长xf=1.4 m,评价得到原始地层压力为45.05 MPa,之后重新绘制诊断曲线1分析时,诊断曲线1和3 平行且截距存在2倍关系,证明计算结果合理。同样地,若该井原始地层压力计算错误(如44.00 MPa),截距的2倍关系将消失,如图13c所示。
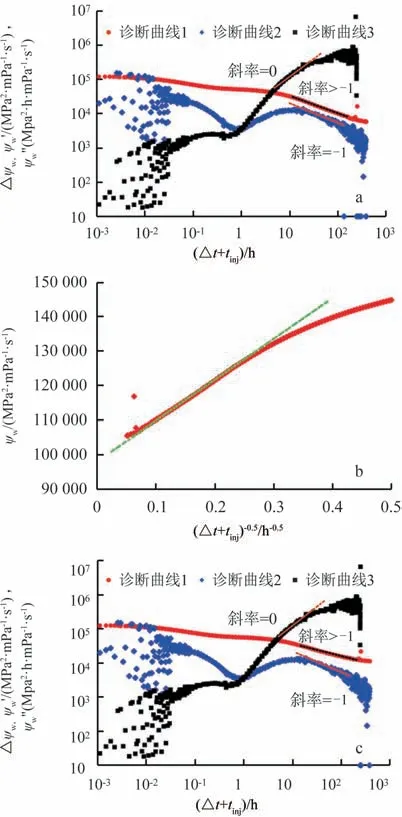
图13 涪陵页岩气田A-1井拟径向流分析结果Fig.13 Results of pseudo⁃radial regime analysis for Well A⁃1 in Fuling shale gas field
通过上述分析,两口井微破裂测试均出现拟径向流阶段,测试效果好,解释可信度高(表4)。两口井解释得到的地层压力和压力系数近似,表明A-3 井保存条件并未受断层影响。且A-3井解释得到的渗透率明显高于A-1井,显示A-3井靠近断层,且天然裂缝发育造成储层物性更好,更接近地质和工程甜点要求[27-29],这也与裂缝闭合前分析结果显示的该井破裂压力较小、地层更容易破裂一致。裂缝闭合前分析方法见参考文献[5]和[12]。
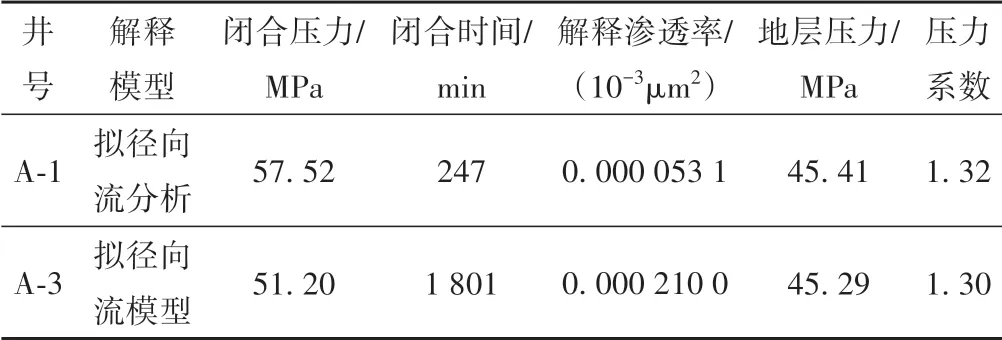
表4 涪陵页岩气田微破裂试井解释结果Fig.4 Results of the mini⁃frac test interpretation in Fuling shale gas field
另外,后续生产动态表明配产6.5×104m3/d时,A-3井所在的井区稳产期平均可达3.0a、可采储量平均为1.20×108m3,而A-1 井所在的井区稳产期仅为1.5a,可采储量0.8×108m3。这均与早期微破裂解释结果认识一致。
通过两口井的分析可以看出,利用本研究提出的微破裂试井解释方法,可以有效地进行现场实际井微破裂测试资料的诊断及分析,解释结果可以帮助正确认识页岩储层压前的物性、含气性及可压性,并为接下来正确划定甜点区和优先部署区提供依据。
5 结论
1)新方法解决了常规关井压力恢复试井分析方法不适用于“短注入期、长衰减期”的问题,在流态诊断的基础上建立分析解释方法,提高了参数解释精度。
2)微破裂测试得到的压力衰减数据若出现拟径向流阶段,诊断曲线1、诊断曲线2 和诊断曲线3 将分别呈现-1,-1 和0 斜率;若出现线性流阶段,诊断曲线1、诊断曲线2 和诊断曲线3 将分别呈现-1/2,-1/2 和1/2 斜率。后两种诊断曲线不受原始地层压力假设值的影响,可以更加准确快捷地识别出正确的流动阶段。
3)拟径向流动阶段的数据可用于评价压裂之前地层的基质渗透率和原始地层压力,线性流阶段的数据可用于评价小型压裂形成的裂缝长度。
4)南川区块平桥背斜两口井的测试解释结果显示,东侧断层并未影响储层保存条件,反而因次生缝较发育导致储层物性更好,更有利于气井压裂及后续稳产。

