基于车-车通信的RBFNN量化滑模控制的ATO算法

杨军霞，张友鹏

(兰州交通大学 自动化与电气工程学院，兰州 730070)

ATO系统是控制城市轨道列车安全运行的核心单元，其最主要的功能是根据不同的列车运行环境实时调整列车的运行速度，使列车能够平稳、精确地跟踪目标位置-速度曲线[1-2].

在高密度运行的城市轨道交通系统中，列车之间信息交互的实时性与可靠性直接影响系统的全局性能及城市轨道交通系统的安全和效率[3].文献[4-6]中，假设列车之间能够精确的传输列车运行的实时状态信息，然而实际的车-车通信信道只具备有限的信道容量，每次只能收发有限的信息，其相互发送的状态信息有可能被截断或丢包，影响列车运行控制性能.因此，本文将控制与通信相结合，设计了一种RBFNN自适应量化滑模控制(radial basis function neural network-adaptive quantization sliding mode control,RBFNN-AQSMC)的ATO控制算法.该算法利用RBFNN对列车模型受到的附加阻力及未知干扰进行自适应逼近补偿，采用量化通信技术，在通信速率尽可能小的情况下，实现列车高精度控制；基于自适应滑模控制技术驱动列车运行状态达到指定的滑动超平面，使列车能够跟踪理想的运行曲线.

1 列车动力学模型

考虑列车运行过程中的外界阻力，根据牛顿动力学原理，基于时间的城市轨道列车单质点运动动力学模型可以描述为：

(1)

g(v(t))=a0+b0v(t)+c0v2(t),

(2)

其中：a0、b0和c0为基本阻力参数.附加阻力f(p(t),v(t),t)由于受线路曲线、坡道和隧道等因素的影响，难以建立精确的模型，本文考虑其为有界时变的动力学情况，用RBFNN并行学习的特点来逼近未知的非线性附加阻力和扰动函数.

为方便控制器的设计，将式(1)重写为：

(3)

其中：x1=p(t)；x2=v(t)；u=F(t)/m为待设计的控制输入，即列车的加速度；g=-g(x2)/m表示列车的基本阻力；f(x)=-f(x1,x2,t)/m表示列车附加阻力及未知的扰动.

2 基于RBFNN的阻力分析

列车在坡度和弯道较大的实际线路条件下运行时，由于线路断面引起的附加阻力及未知干扰可能较大，会造成列车控制精确降低、跟踪性能下降、列车运行效率降低等问题，影响行车.因此，采用RBFNN对式(3)中的f(x)进行学习评估，主要解决系统由于动力学模型简化、模型参数不确定和外界环境变化等因素导致的较大跟踪误差问题，以加强ATO系统的自适应和抗干扰能力.

RBFNN是一种高效的、局部收敛的前馈网络，具有简单的结构、很快的学习速度和良好的泛化能力，理论上能够以任意小的精度逼近任何光滑非线性函数，可视为万能逼近器，在自适应非线性系统中有很多研究成果[8-9].

本文选择三层的RBFNN结构(见图1)，输入层由信号源节点构成，隐含层的神经元数视f(x)的精确要求等具体情况而定，输出层输出对输入层的响应.为了加快学习速度并有效的避免局部极小问题，由输入到输出的映射是非线性的，而由隐含层到输出空间的映射则为线性.输出层的输出是隐含层输出信号的线性加权和，通过调整合适的输出权值参数，实现f(x)的逼近.RBFNN的函数逼近能力由如下引理给出.

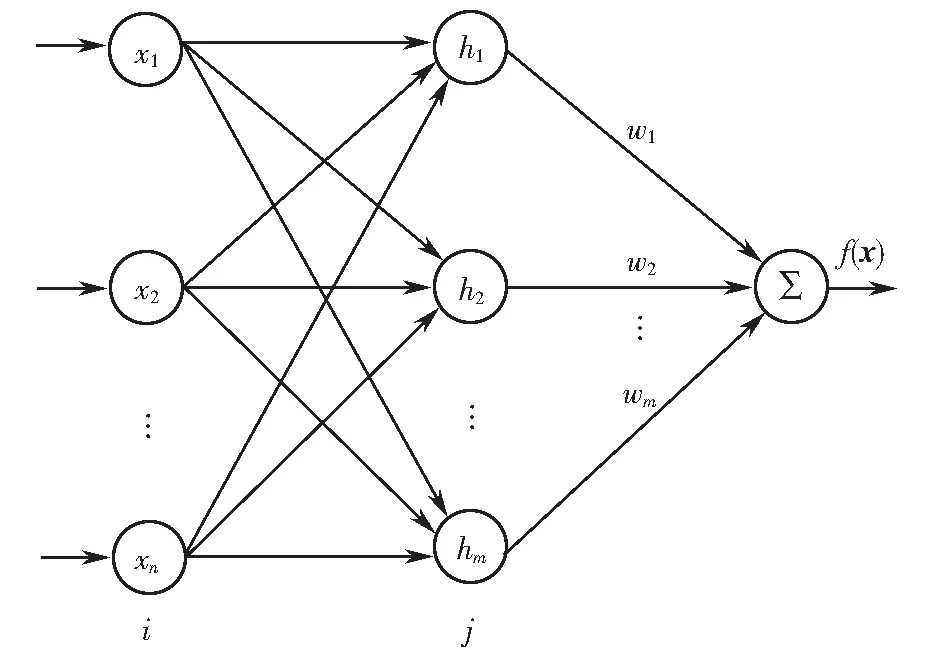
图1 RBFNN结构

引理1[10-11]任意未知的光滑非线性函数f(x)可以用RBFNN以f(x)=WTh(x)的形式逼近，其中：x=[x1,x2,…,xn]T⊂Rn为网络的输入，n为输入向量的维数；W=[w1,w2,…,wm]T是可调节的权值参数向量，m为隐含层的神经元个数；h(x)=[h1(x),h2(x),…,hm(x)]T为隐含层的输出向量；hj(x)为隐含层第j个神经元的输出，

(4)

其中：j=1,2,…,m；‖·‖为欧式范数；cj，bj分别为隐含层第j个神经元的中心和宽度参数，宽度向量b=[b1,b2,…,bm]T，且bj>0,中心点的坐标向量为

c=[cj1,cj2,…,cji,…,cjn]T,i=1,2,…,n.

(5)

通过设置合适的隐含层神经元数，RBFNN能够在紧致工作域Θx⊂Rn上以任意精度逼近未知函数f(x)，

f(x)=W*Th(x)+ε(x),

(6)

其中：W*为所有估计权值中使ε(x)最小的权值向量，

(7)

ε(x)为一个很小且有界的逼近误差，即|ε(x)|≤ε*.

RBFNN的输入取x=[x1x2]T，则输出为

(8)

定义误差函数

(9)

3 RBFNN自适应量化滑模控制器设计与分析

在基于车-车通信的多列车协同控制运行模式下，考虑车-车通信性能对控制系统的分析和设计具有重要的意义[12].本文考虑的车-车通信的拓扑结构如图2所示.图2中，T1表示第一列列车，以此类推，箭头表示数据(列车运行方向、位置、速度、加速度等)传输的方向.在实际的列车通信环境中，列车之间的通信信道只具备有限的信道容量，相邻的列车之间每次通信只能收发有限的信息，在这种通信约束下，列车之间相互发送的实值状态有可能被截断或丢包；因此，为了保证系统可以在给定的带宽内正常运行，需要采用量化技术减小列车之间通信的速率.本文选用对数量化器对列车运行非线性系统的控制输入值u(前车向后车传输的加速度信息)进行设计与分析.

图2 车-车通信的拓扑示意图

3.1 控制器设计

引理2[13]对数量化器为

Q(u)=θround(u/θ),

(10)

其中：Q(u)为有界时变的系统控制输入u的量化值；θ为量化水平.

为便于对数量化控制器的设计，令Q(u)=q1(t)

u+q2(t)[14]，取：

(11)

(12)

结合式(3)和引理2，将式(3)表述为：

(13)

定义列车位置和速度跟踪误差为：

e1=x1-xd,

(14)

(15)

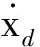
(16)

设计滑模函数为[15]

s=ce1+e2,

(17)

其中：c>0为可调节的设计参数.对s两侧进行微分，得

(18)

其中：a*=a0/m；b*=b0/m；c*=c0/m.参数a*、b*和c*随不同的车型、载重、运行环境及天气情况等因素而发生变化，造成列车动力学模型参数的不确定性[16].因此，本文引入自适应控制机制，以应对列车模型参数的变化，保证控制系统的控制性能.

设计如下的控制律和自适应律：

(19)

(20)

(21)

(22)

(23)

(24)

(25)

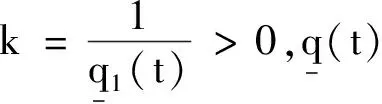
3.2 系统稳定性分析

定理1根据式(13)描述的列车动力学模型，设计系统的控制器(式(19)、(20))、自适应律(式(24))、基本阻力戴维斯方程系数的自适应律(式(21)～(23))、RBFNN逼近附加阻力和未知扰动的权值向量自适应律(式(25))，则列车在基本阻力戴维斯方程系数不确定、附加阻力及扰动不可精确建模的状态下能够实现对给定的列车运行曲线的实时跟踪，且闭环系统稳定.闭环系统的初始状态满足

其中：ζ为任意大小的正常数；α、β、c、ρ、χ、Γ、λi和σi为控制参数，i=1,2,…,5.

证明：选取Lyapunov函数为

(26)

对式(26)两侧进行微分，得

(27)

将式(18)～(25)代入式(27)，并整理得

(28)

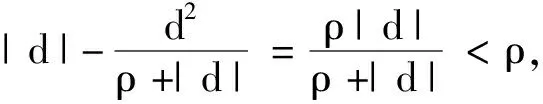
(29)

(30)

于是，式(28)可以表示为

(31)

根据Young′s不等式的性质，可得：

(32)

(33)

(34)

(35)

(36)

(37)

(38)

将式(32)～(38)代入式(31)，并整理可得

(39)

定义：

μ=min[2(α-1),λ1σ1,λ2σ2,λ3σ3,χσ4,Γσ5],

(40)

(41)

则

(42)

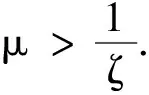
4 仿真实验

图3 列车运行期望速度与距离曲线

基于定理1得到的仿真结果如图4～6所示.图4给出了列车对于给定的期望位置曲线的跟踪及其跟踪误差的情况，图5给出相应的速度跟踪及其误差情况，图6给出未经量化和经过量化后的控制输入.从图4～5可以看出:本文所设计的RBFNN-AQSMC算法具有较好的跟踪性能，能够以较高的控制精度实现对目标距离和速度曲线的跟踪.特别地，由图4所示的位置跟踪误差放大示意图可以看出：控制算法的位置跟踪误差在-0.1～0.2 m，其控制效果超过列车在制动阶段规定的列车控制误差小于±0.2 m的控制要求，有效地提高了列车的控制精度.由图6可知：控制输入连续信号经过量化后变换为分段恒定信号，方便车-车的信息在信道中的传输.因此，本文提出的RBFNN-AQSMC算法验证了所设计的控制和通信相结合的控制策略在基于车-车通信的列车运行控制系统中的有效性.

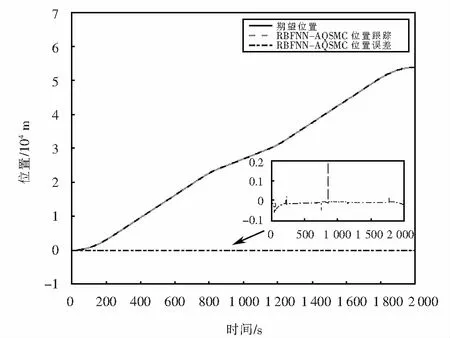
图4 位移跟踪效果

图5 速度跟踪效果

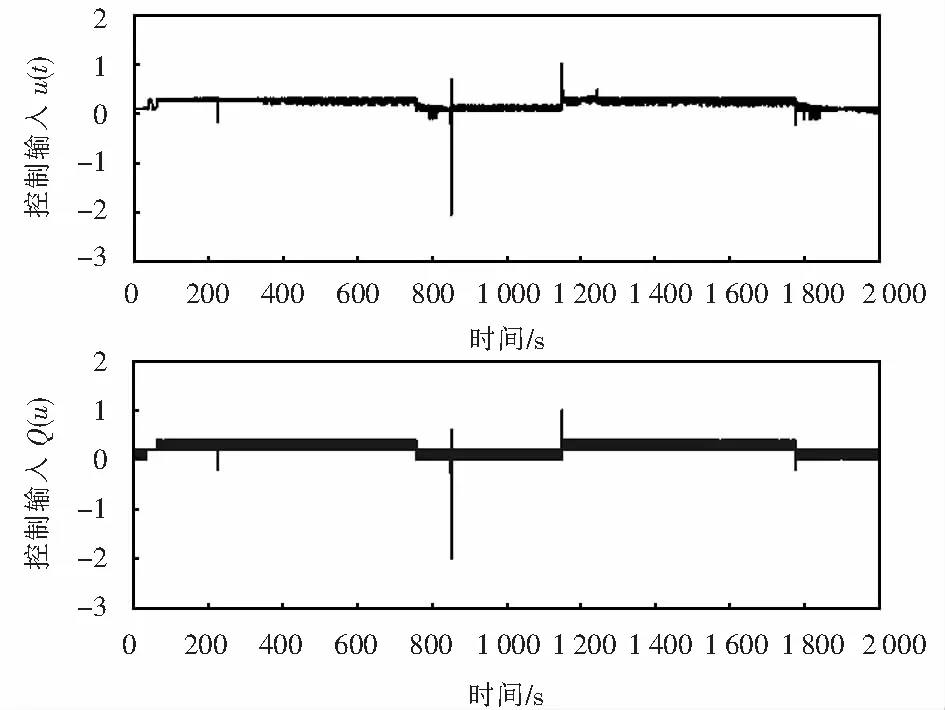
图6 控制输入曲线

5 结论

在基于车-车通信的列车运行控制系统中，对ATO控制算法和列车之间信息交互的实时性和可靠性要求增高.为此，本文将列车控制和车-车通信相结合，利用自适应量化控制方法对RBFNN列车运行模型的控制输入进行量化处理，并基于滑模控制原理设计了具有自适应机制的控制器.理论证明和仿真实验结果表明：RBFNN-AQSMC控制方法能够保证城市轨道列车在运行外界阻力未知和列车之间通信速率极小的情况下，仍能保持系统稳定，并对目标位移和速度曲线进行高精度的跟踪，有效地解决了列车运行控制系统列车信息交互信道容量约束产生的控制精度问题，为多列车协同控制系统的研发及评估提供借鉴.