非参数化蒸散发估算方法在华北灌溉农田的适用性评价*

张晓龙,张玉翠,石嘉丽,2,王 妍,2,3,沈彦军,2**

(1.中国科学院遗传与发育生物学研究所农业资源研究中心/中国科学院农业水资源重点实验室/河北省节水农业重点实验室 石家庄 050022; 2.中国科学院大学 北京 100049; 3.河北师范大学资源与环境科学学院/河北省环境演变与生态建设实验室 石家庄 050024)

蒸散发是水分从地表进入大气的过程,是土壤蒸发、冠层截留和植物蒸腾的总和。蒸散发是能量、水分和碳循环过程中的重要纽带,也是区域水资源重要的消耗途径。在全球范围内超过60%的降水通过蒸散发返回大气,而在干旱区、农田这一比例甚至超过90%。蒸散发以潜热通量(latent heat flux,LE)的形式消耗了大约50%的地表吸收的太阳辐射量。因此,精准估算蒸散发已成为水量平衡计算、农业水资源管理、水文模拟等众多领域共同关注的核心问题。

尽管蒸散发可通过涡度相关系统、蒸渗仪、Bowen 比、大孔径闪烁仪等方法直接观测,但由于这些原位技术的局限性,估算大尺度、长期蒸散发仍然是一项重大的挑战。因此,许多直接或间接的估算方法被提出,包括Penman 公式、Penman-Monteith 公式、经验统计方法、地表能量平衡法、SPAC 系统模拟方法、互补相关理论方法、陆面过程与数据同化方法等。然而,大多数估算方法都比较复杂或需要对地表性质有详细了解,从而限制了这些方法的应用,降低了估算精度。例如,Penman-Monteith 方程需要输入冠层阻力,Shuttleworth-Wallace 方法需要空气动力特性、冠层粗糙度和土壤阻力,但这些参数在区域尺度上很难测量和校准。近年来,Liu 等提出了一种基于哈密顿广义能量原理的非参数化地表蒸散发估算(the nonparametric approach,NP)方法。NP 方法只需要地表净辐射、空气温度、地表温度和土壤热通量作为输入,克服了传统蒸散发估算方法中存在经验参数化的物理缺陷,降低了计算过程的不确定性。该方法所有必要的输入均为可测量的,为实际应用提供了一个新颖而简单的方法。目前,该方法已在部分站点进行了验证,并结合遥感数据和气象驱动数据进行了区域蒸散发适用性检验。Liu 等利用全球26 个涡度相关站点观测结果对NP 方法进行了评价,其中23 个点性能表现良好; 并进一步表明NP 方法与Penman-Monteith 方法在性能上是兼容的。Yang 等发现NP 方法在干燥条件下会高估蒸散发,应避免在干燥条件下应用,而在湿润条件下表现良好。王宁等对比发现在湿润下垫面NP 方法会低估蒸散发,在干旱下垫面会高估蒸散发,且夏季估算精度优于冬季; 并利用遥感数据估算了黑河上中游区域蒸散发,结果表明虽然存在一定误差,但能够反映区域蒸散发分布特征。Pan 等在黑河流域6 个站点验证了NP 方法的有效性,并基于该方法和遥感数据估算了黑河流域蒸散发,结果表明遥感反演的蒸散发时空分布基本可靠,但在非植被站点,估算值与地面观测值一致性较差,而相对误差较小。总的来说,NP 方法有必要在不同区域或生态系统进行更细致的适用性分析,以识别出有助于提高估算精度的误差源。

华北平原是我国主要的灌溉农业区和重要的粮食生产基地,对保障国家粮食安全具有举足轻重的作用。该地区种植结构以冬小麦()和夏玉米()为主,其种植面积约占粮食总播种面积的80%左右。该地区降水量少且集中于夏季,无法满足作物生长需求,灌溉成为维持和提高粮食产量不可缺少的手段。农田灌溉改变了区域水热条件与气候,直接和间接地影响了蒸散发过程。精准地估算灌溉农田蒸散发不仅对华北平原干旱监测和水资源管理具有重要理论意义,而且对区域种植结构调整和生态环境建设具有重要实践意义。目前关于NP 方法应用研究大多集中于干旱区流域,关于半湿润区灌溉农田的适用性分析报道较少。因此,本文主要利用华北灌溉农田区的栾城农业生态系统试验站(简称栾城站)、禹城综合试验站(简称禹城站)和馆陶试验站(简称馆陶站)3 个通量站点的观测数据,应用NP 方法估算这3 个站点30 min 和日尺度蒸散发(以LE 的形式),并以涡度相关系统修正的LE 为参考,分析NP 方法在华北平原灌溉农田不同季节和不同时间尺度的适用性,该研究不仅为NP 方法改进提供参考,而且也有助于加深对蒸散发理论的认识。

1 研究站点及数据处理

1.1 研究区及观测站点概况

华北平原位于太行山以东,黄河以北,燕山以南,渤海以西,面积约14.1 万km。该地区土层较深,海拔低于100 m,跨越北京、天津、河北、河南、山东等多个地区。该地区属于暖温带半湿润半干旱大陆性季风气候,年平均气温10.0～14.2 ℃,光照充足。主要粮食作物为小麦、玉米,主要经济作物为棉花(spp.)、果树和蔬菜(图1)。年平均降水量为400～500 mm,70%发生在夏季,农业灌溉消耗了地下水总量的80%以上。本研究以华北灌溉农田为研究对象,选取栾城站(37°53′N,114°41′E,海拔50 m)、禹 城 站(36°49′N,116°34′E,海拔22 m)和馆陶站(36°30′N,115°07′E,海拔30 m) 3 个通量观测站点,栾城站和禹城站下垫面均为充分灌溉管理下的典型冬小麦-夏玉米一年两熟轮作制农田生态系统,而馆陶站下垫面为冬小麦/夏玉米和棉花综合下垫面。各通量站下垫面均匀且地势平坦,满足通量观测源区要求,观测样地具有较强的代表性。一般情况下,冬小麦10月初播种,次年6月中旬收获; 夏玉米6月中旬播种,9月底收获; 棉花4月底播种,10月底收获。根据农田生态系统水分、土壤、气象和生物监测规范和野外田间试验要求,各站配备有国际先进的仪器设备。涡度相关系统主要由红外开路式CO/HO气体分析仪和三维超声风速仪组成,同时辅助有辐射分量、常规气象要素、土壤热通量的同步观测,为该研究提供所需的观测数据。

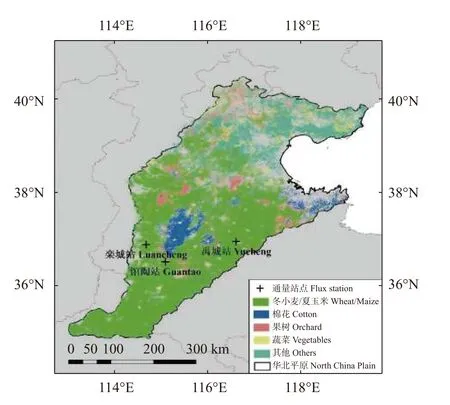
图1 华北平原作物类型空间分布及通量站点位置Fig.1 Spatial distribution of agricultural land-use types and location of flux stations in the North China Plain

1.2 数据处理

本研究使用的通量数据是各站点提供的经过质量控制的二级产品,包括30 min 平均LE 和感热通量(sensible heat flux,)。由于仪器故障、不利的微气象条件、异常值剔除和质量控制等原因造成数据缺失,通常一年中约有17%～50%的观测数据缺测或被剔除。在水资源管理或水文模型研究中,通常需要得到日、月甚至年的累加值,本研究使用德国耶拿大学提供的R 软件ReddyProc 包进行数据插补,并进一步统计为日平均值。

涡度相关技术目前已成为获得生态系统LE 和的标准观测手段之一,但是该方法普遍存在能量不闭合的问题。现有能量闭合校正方法主要有两种类型,即Bowen 比闭合修正(BR)方法和能量残差闭合修正(ER)方法。虽然两种闭合修正方法都可能对系统内的能量和水平衡检测中有重大或潜在的不利影响,但对于大多数地表条件,采用ER 修正后的潜热通量与各估算方法模拟结果的一致性更高。因此,采用ER 方法修正的LE 作为评价本研究蒸散发估算方法的基础。ER 方法表达公式如下:

式中:LE为能量残差法修正后LE (W∙m),为涡动相关系统测量的(W∙m),为地表净辐射(W∙m),为土壤热通量(W∙m)。

为保障数据一致性,将辐射分量、空气温度、地表温度、土壤热通量等10 min 频率观测数据统计为30 min 和日平均值; 而降水统计为累加值。

2 研究方法

2.1 非参数化蒸散发估算方法

在NP 方法中,在宏观层面上假设下垫面为均匀的,哈密顿量(势能与动能的总和)为该系统的总能量。作为势能,则、和LE 为动能; 地表温度()作为这个系统的广义坐标。该方法计算了哈密顿量关于的偏微分方程,详细推导过程见文献[21]。计算公式如下:

式中:LE为NP 估算得到的LE (W·m);为地表空气温度(K); ϵ为地表比辐射率,由于数据的限制,本研究假设 ϵ为常数,在农田下垫面站取0.95; σ为Stefan-Boltzman 常数(5.67× 10W∙m∙K); γ为干湿表常数(kPa∙℃),可用近地表压力来估算; ∆为时的饱和水汽压梯度(kPa∙℃),其计算公式如下:

2.2 精度评价方法

本研究选取平均偏差(Bias)、相对误差(RE)、决定系数(R)、均方根误差(RMSE)和Nash-Sutcliffe效率系数(NSE)来量化估算方法模拟精度。其计算公式如下:

2.3 敏感性分析方法

为了检测模型各驱动变量对输出结果的贡献,本研究采用简单的相对敏感系数法进行敏感性分析。在这个方法中,通过比较改变输入变量产生的LE(LE)相对于参考LE (LE)的比例来计算每个变量的敏感性。本研究中所有输入变量的变化范围设为±30%,取其中一种输入参数逐步变化5%,而其他输入参数保持不变。敏感系数(S)计算公式如下:

3 结果与分析

3.1 通量站点能量闭合分析

本文用线性回归方法和能量平衡比法分析了栾城、禹城和馆陶3 个站点的能量平衡状况(图2)。其中,线性回归方法中斜率代表能量平衡程度,理想状况下斜率为1,截距为0,但实际情况下截距通常不为0; 能量平衡比(EBR)即较长时间段(如1年)热通量之和(LE+)与可利用能量(−)的比值,通常EBR 范围为0.34～1.69。从图中可以看出,在日尺度上,栾城、禹城和馆陶3 个站点的能量闭合率分别为83.7%、87.4%和51.7%,EBR 分别为0.95、1.06和0.94; 在30 min 尺度上这3 个站点的能量闭合率分别为81.1%、84.5%和73.7%,EBR 分别为1.13、1.06 和0.95。可知,3 个站点的EBR 接近于1,说明这3 个站点数据公开前已经过数据质量控制; 栾城站和禹城站能量闭合率更好一些,且日尺度和30 min 尺度能量闭合率相差不大,表明这两个台站数据质量相对更好一些。需说明的是,理论上每个站点的EBR 在不同时间尺度上应是基本一致的,但本研究中栾城站2月份因缺少部分数据,故栾城站日尺度和30 min 尺度EBR 存在较大差异。一般认为,如果能量闭合观测误差超过10%,其观测结果对大气模式特别是陆面过程模式的检验是不能接受的。本研究发现,即便这3 个站点经过严格的质量控制,依旧有超过12.6%以上的能量丢失,这样会造成LE 低估现象。另外,随着蒸散发估算理论和遥感技术的发展,需要提供较可靠的地面验证数据,所以对通量观测数据的校正十分有必要。

图2 日尺度和30 min 尺度上3 个站点通量站点的能量平衡特征Fig.2 Energy balance characteristics of flux stations at daily scale and 30 min scale in the three stations

3.2 灌溉农田蒸散发估算

基于NP 方法,利用通量站观测的、、和等数据,估算了2010年的栾城、禹城和馆陶3 个华北平原典型灌溉农田的日尺度和30 min 尺度的LE,将估算值LE与修正后的通量观测值LE进行对比验证分析。需说明的是,在30 min 尺度上,栾城站在2月缺失部分数据,剔除不用。表1 显示了2010年3 个通量站点观测的能量通量和环境参数均值。从表中可知,3 个站点的各输入参数值相差不大,LE从大到小依次为栾城站、禹城站和馆陶站;而降水量与LE呈反比,这可能是由于灌溉活动保证了下垫面较稳定的水分条件,在一定灌溉保证率的农田中降水并不是蒸散发的控制因素; 栾城站、禹城站和馆陶站潜热比(LE/)分别为81.6%、82.3%和72.3%。栾城站和禹城站的潜热比很接近,这可能与两站下垫面条件更接近有关。农田蒸散发在很大程度上受可利用能量控制,栾城站和禹城站潜热比类似,栾城站可利用能量大于禹城站,故栾城站蒸散量大于禹城站; 另外,下垫面作物类型对农田蒸散发也有较大影响,如禹城站和馆陶站具有接近的可利用能量,但由于禹城站下垫面为冬小麦/夏玉米轮作农田,馆陶站则是冬小麦/夏玉米和棉花混合下垫面,导致馆陶站蒸散量明显低于禹城站。因为这3 个站点土壤类型、质地差别不大,可忽略其影响。综上,由于灌溉活动保证了下垫面较稳定的水分条件,所以华北平原灌溉农田蒸散发的主要影响因素为可利用能量和作物类型。

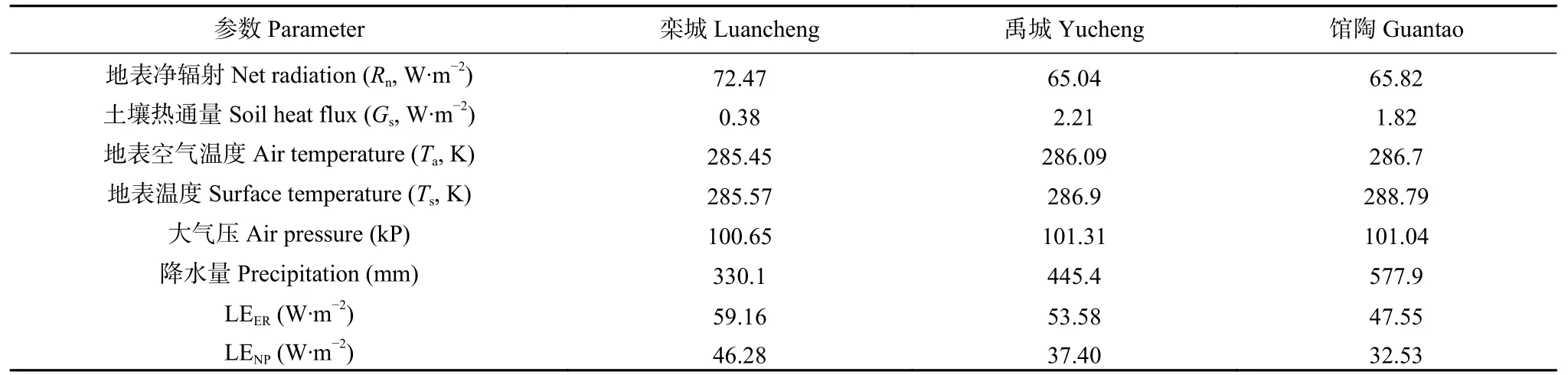
表1 3 个通量站点能量通量和环境参数平均值Table 1 Average of energy fluxes and environment parameters at the three stations

3.3 非参数化方法估算结果精度评价

图3 为2010年的栾城、禹城和馆陶LE 逐日过程及与观测值的对比结果。总体而言,栾城站和禹城站蒸散发在年内明显呈双峰型,馆陶站则呈不明显的双峰型,模拟效果可以较好地反映蒸散发年内变化过程。从箱体图结果可知,在灌溉农田中NP 方法总体上低估LE,栾城、禹城和馆陶站LE的均值较LE分别低12.88 W∙m、16.18 W∙m和15.02 W∙m,平均低估14.69 W∙m; 另外,LE年内波动范围大于LE。在日尺度上综合所有站点的LE与LE之 间 的Bias、RE、、RMSE 和NSE分别为−14.73 W∙m、 27.5%、 0.81、 27.75 W∙m和0.71(表2)。总之,在日尺度上NP 方法在3 个农田站点总体表现较好,且栾城站模拟精度优于馆陶站和禹城站。

表2 日尺度和30 min 尺度3 个站点的蒸散发估算精度评价Table 2 Accuracy evaluation of evapotranspiration estimates at daily scale and 30 min scale in the three stations

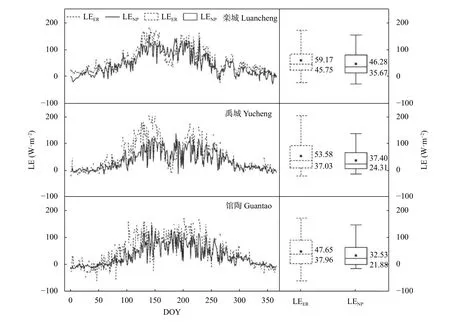
图3 日尺度上3 个站点的潜热通量(LE)年内变化过程及估算结果对比Fig.3 Comparison of latent heat flux (LE) between estimation and observation at daily scale in the three stations

因30 min 尺度数据量庞大,不便完整展示,本研究 以2010年9月1日0 点 至9月15日23 点30 分完整时间段为例,展示栾城、禹城和馆陶3 站的LE日内变化过程及与观测值的对比结果(图4)。该时间段夏玉米为乳熟期、棉花为吐絮期,作物生长趋于成熟; 并且该时间段内3 站有明显的降水过程,降水量存在较大差异。从图中可知,在示例时间段内30 min 尺度上,LE与LE高度一致,估算结果能较理想地反映LE日内变化过程,即使是阴雨天气精度依旧很好。经计算,3 个站点该时间段内R可达0.97～0.99,NSE 可达0.96。在30 min 尺度上综合2010年全年所有站点的LE与LE之间的Bias、RE、、RMSE 和NSE 分别为−10.34 W∙m、21.5%、0.88、40.37 W∙m和0.87(表2)。30 min 尺度上,非参数方法在栾城站模拟精度优于馆陶站和禹城站。相比于日尺度,非参数方法在3 个农田站点总体表现除RMSE 指标外均有所提升,表明该方法在30 min 这样短时间尺度上表现更好。总之,NP 方法在灌溉农田低估LE,但是可以较好地捕捉LE 的年内和日内变化过程,具有较高的应用价值。

图4 30 min 尺度上3 个站点的潜热通量日内变化过程及估算结果对比(9月1—15日)Fig.4 Comparison of latent heat flux between estimation and observation at 30 min scale (from September 1st to 15th) in the three stations

3.4 非参数化方法在不同季节的适用性

从3 个站点不同季节的估算精度分析指标(图5)可以看出,在日尺度和30 min 尺度上NP 方法呈现季节变化的相似性,但在RE 和NSE 的量级上存在差异。Bias 整体上呈负值,最小值出现在4、5月份; RE 在冬季误差较大,在作物生长季表现稳定且良好;年内变化呈双峰型,与年内各月LE 变化过程一致,即当LE 较高时可达0.8 以上,而在LE较低时(冬季和夏玉米苗期)普遍低于0.4; RMSE整体上呈单峰型,在日尺度上,RMSE 最大值出现在4、5月份,而在30 min 尺度上,RMSE 最大值出现在5、6月份; NSE 在各月的表现类似,作物生长季表现优于非生长季,且30 min 尺度表现优于日尺度。总体上,NP 方法在生长季估算精度高于非生长季,玉米估算精度高于小麦,夏季估算精度高于冬季。

图5 日尺度和30 min 尺度3 个站点的蒸散发估算精度在各季节上的评价Fig.5 Accuracy evaluation of evapotranspiration estimates at daily scale and 30 min scale in the three stations

3.5 非参数化方法敏感性分析

为了分析各输入参数对估算结果的影响,本研究分别在日尺度和30 min 尺度上对NP 方法各参数进行敏感性分析。NP 方法输入参数包括、、和,选取其中一种参数从变化±5%到±30%,而其余参数保持不变,得到各参数敏感性(图6)。从图中可知,和的敏感度与参数变化同向,和的敏感度与参数变化异向。日尺度上、、和参数变化5%时的敏感性系数在3 个站点平均分别为11.3%、−10.4%、6.0%和−0.24%; 30 min 尺度上这4 个参数变化5%时的敏感性系数分别为11.75%、−10.94%、6.24%和−0.38%。相对于站点来说,在日尺度上,参数、和敏感程度馆陶站>禹城站>栾城站,而敏感程度禹城站>馆陶站>栾城站; 在30 min 尺度上,参数和敏感程度馆陶站>栾城站>禹城站,敏感程度馆陶站>禹城站>栾城站;敏感程度禹城站>馆陶站>栾城站,影响可忽略不计,例如当在敏感度最高的站点(禹城站)和时间尺度上(30 min)变化−30%时,LE 仅变化2.66%。总体而言,无论在日尺度上还是在30min 尺度上,各参数的敏感性在各站点上没有明显差别,相较而言馆陶站敏感性最高; 各参数敏感度依次为、、和。鉴于此,虽然是对通量站地表能量平衡的重要分量,但当缺乏土壤热通量观测仪器埋深和土壤质地等数据缺乏时,可不考虑埋深(仪器以上土壤热储存量)对的影响。

图6 非参数化方法在3 个站点的参数敏感性分析Fig.6 Sensitivity analysis of the parameters of the nonparametric approach in the three stations

4 讨论

4.1 潜热通量修正的影响

涡度相关方法目前已被广泛应用于陆地生态系统水碳循环过程研究,其测定的LE 结果常作为实际蒸散发“验证值”来完善或改进蒸散发估算模型的参数化方案。然而,该方法的测量误差可能对模型精度评价产生直接影响,其中30 min 尺度上LE 的标准误差约为5%～20%,从30 min 到日的时间尺度上升会导致出现5%～10%的偏差。另外,基于涡度相关技术的能量平衡研究一直受到能量不闭合问题的挑战,该问题是近30年来困扰地-气交换试验研究的主要难点之一。大量观测结果表明,几乎每个观测站都存在地表能量平衡不闭合的问题,一般湍流通量(包括LE 和)仅占地表可利用能量的70%～90%。

Bowen 比闭合修正(BR)方法和能量残差闭合修正(ER)方法是目前最常用的两种方法。BR 方法是根据Bowen 比分配剩余能量到LE 和中,假设LE和具有相似的观测精度,然而根据原位观测数据,涡度相关系统对的观测精度要高于LE 的精度;此外,比LE 的随机误差的季节差异更小。因此,当对和LE 测量的准确性水平存在显著差异时,应谨慎使用BR 方法。ER 方法是基于能量平衡原理,这种方法只依赖于、和的测量精度,但是这种修正方式将不闭合的能量全部归于LE 值中,不可避免的会高估LE。当空气储热、冠层储热、地表到土壤热通量板之间的土壤储热过高时,ER 方法也会引起较大误差。此外,使用Bias、RE、、RMSE和NSE 等指标来表示模拟值与观测值之间的误差,通常假设将所有误差都归结于模拟值中,即认为观测值无误差。然而,这种假设在实际上几乎不可能发生,观测值的选取及校正方法的使用会直接影响精度评估结果,所以只有固定“真值”(观测值)时对比精度评估结果才有意义。本研究以日尺度为例,分别将LE对比未修正的LE (LE)、BR 方法修正的LE (LE)和ER 方法修正的LE(LE)进行验证,精度评价相关参数见表3。从表中可知,两种修正方法使得LE与LE和LE一致性指标(、RMSE 和NSE)均有所提升,偏差性指标(Bias 和RE)略有下降;其中3 个站点平均的分别从0.57 提升到0.80 和0.82,RMSE 分别从33.41 W·m下降到26.80 W·m和27.50 W·m,NSE 分别从0.42 提升到0.69 和0.71,Bias 分别从−13.76 W·m下降到−14.86 W·m和−14.73 W·m,RE 分别从26.1%下降到28.1%和27.9%。相较而言,ER 修正后一致性优于BR 修正,该结果与上述文献结果一致。本研究目的是验证蒸散发估算方法的适用性,需提供一个较稳定可靠的验证值,相较而言,ER 方法更适合灌溉农田的LE 修正,故本文选择利用ER 方法修正潜热通量作为评价本研究蒸散发估算方法的基础。但值得注意的是,也许因为LE也是基于能量残差进行计算,LE和LE并非完全独立,导致ER 方法修正结果表现更强的一致性,故最佳的能量闭合修正方法的选择仍有待进一步探索。

表3 日尺度上3 个站点的不同修正方法的潜热通量对模拟结果的精度评价Table 3 Accuracy evaluation of simulation results by latent heat flux of different correction methods at daily scale in the three stations

4.2 非参数化方法适用性检验

实际蒸散发精准估算一直是水文、微气象学研究领域的研究难点之一。NP 方法提供了一种新颖而简单的估算方法。虽然NP 方法基于简化的空气动力阻力框架,并结合平衡蒸发和的变化来估算LE,但该方法因减少了输入变量的累积误差,反而具有其他估算模型(Penman-Monteith 公式)相当的精度; 实际上,由于不同作物的空气动力学阻力不同,采用通用稳定函数计算的空气动力学阻力可能会产生较大的误差。由于观测数据限制,本研究未检验NP 方法在月、年这样的长时间尺度的表现,有待将来进一步研究。本研究基于华北3 个灌溉农田站点在日尺度和30 min 尺度上进行了NP 方法适用性检验,结果表明,NP 方法可以较好地反映季节及日内变化特征,在日尺度和30 min 尺度上总体表现较好,且在不同站点没有产生显著的预测误差。另外,NP方法在玉米生长季估算精度高于小麦生长季,主要原因可能是NP 方法对灌溉活动反应不敏感,并不能充分反映灌溉对农田蒸散发的影响。玉米生长季为7月至10月,华北平均降水多集中于该时期,基本可保证作物生长需求,而小麦生长季为11月至次年6月,期间降水较少,无法满足作物生长需求,特别是在返青−拔节期,需要进行大量灌溉; 因NP 方法对灌溉事件响应能力不足,使得小麦季低估较玉米季更严重,且模拟精度更差,总体而言,NP 方法在华北灌溉农田不同作物类型、不同时间尺度与参考值具有较高的一致性,但在水分供应较充足时较严重低估LE,而在较干燥时轻度低估或不低估LE; 另外该方法对灌溉活动的响应考虑不足,有待进一步改进以提高灌溉农田模拟精度。本研究结果与已有文献结论基本一致。

研究发现,NP 方法不仅可以较好地反映LE 的日内变化、季节变化,而且基本不受阴雨天气影响(图4),这不仅表明NP 方法的稳健性,更表明因不受云层的影响而展示出在遥感应用中巨大潜力; 这与Liu 等研究结果一致。另外,值得注意的是,蒸散发估算值虽然整体被低估,但存在季节性差异(图3)。为进一步分析不同月份LE与LE散点关系的差异,本研究分析了日尺度和30 min 尺度上栾城站、禹城站和馆陶站LE(轴)与LE(轴)之间的散点关系(图7、图8)。从图7 可以看出,栾城、禹城和馆陶3 站潜热通量计算值和观测值有较好的相符性,决定系数为0.80～0.83,3 站综合为0.81; 一元线性拟合斜率低于1,且大部分点低于1∶1 线,表明蒸散发估算值整体被低估。值得注意的是,栾城站和禹城站偏离出95%预测带的值集中于6月和7月,仅低估−1.38 W∙m,并且主要表现为高于预测区间; 而馆陶站6、7月份低估−23.5 W∙m。这种现象的主要原因可能是栾城站和禹城站下垫面为冬小麦、夏玉米轮作,而馆陶站是冬小麦、夏玉米轮作和棉花的混合下垫面。6月中旬到7月上旬是冬小麦收获后,而夏玉米七叶期之前的阶段,该阶段作物叶面积指数较低,尚不能覆盖地表,下垫面性质类似裸地到稀疏草地之间。在植被生长茂盛时,NP 方法低估LE,在裸地或植被稀疏时高估LE 的现象与上述文献结果可相互验证。

图7 日尺度上3 个站点的潜热通量(LE)估算结果与观测结果的比较Fig.7 Comparison of latent heat flux (LE) between estimation and observation at daily scale in the three stations

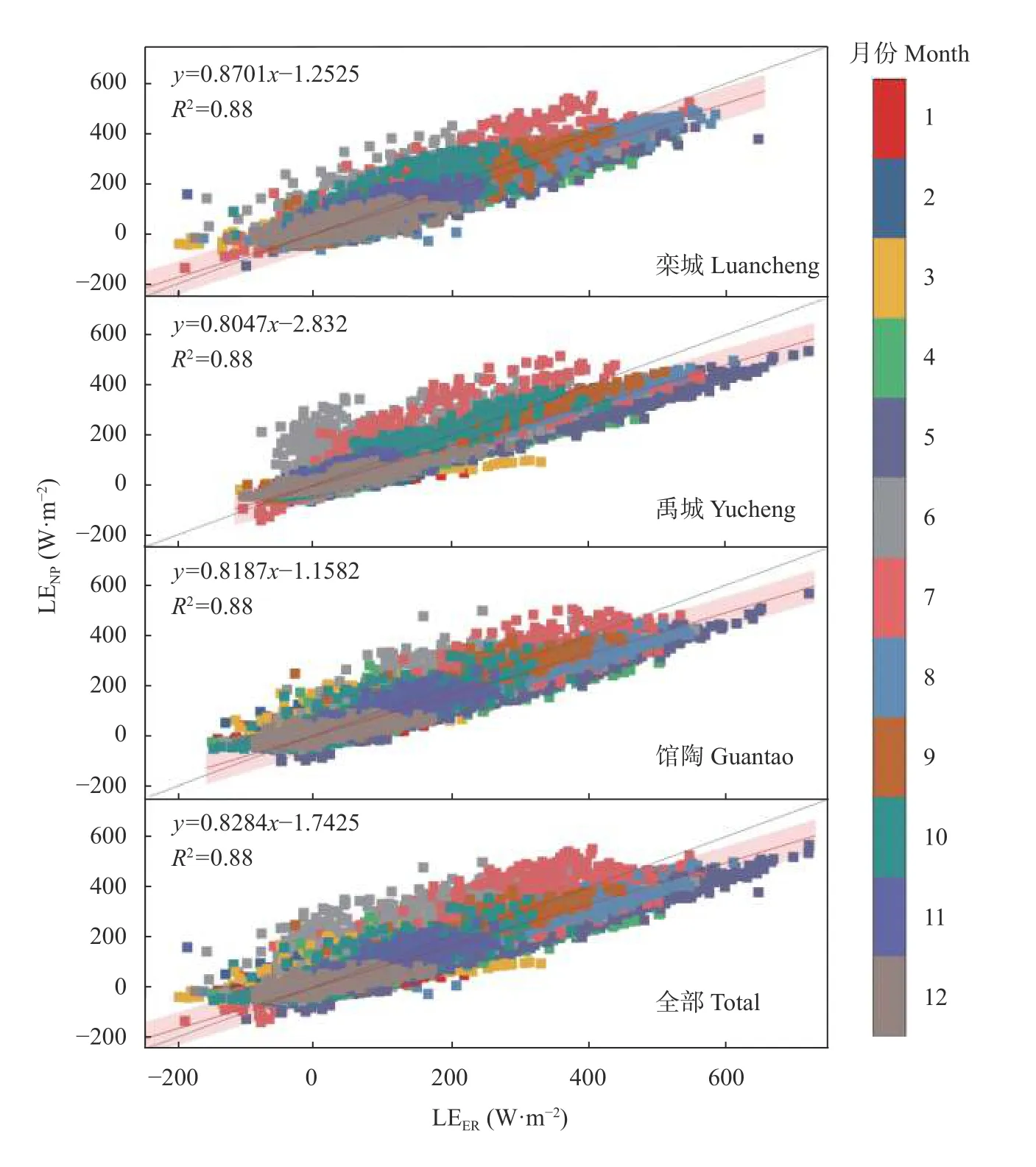
图8 30 min 尺度上3 个站点的潜热通量(LE)估算结果与观测结果的比较Fig.8 Comparison of latent heat flux (LE) between estimation and observation at 30 min scale in the three stations

NP 方法所产生的残差可能受到若干不确定来源的影响,包括NP 方法固有局限性、能量闭合通量校正、土壤热通量校正以及气象变量的测量误差。能量闭合修正的影响已在上文讨论。对测量深度的进行校正可以改善2%～5%的能量闭合,进而NP方法估算精度评价。地表温度1 K 的误差大约会导致13 W·m的误差。的测量误差通常小于5%。测量精度通常较高,但因为测量高度的差异,换算成2 m 的标准高度时,会产生一定误差。而从NP 方法固有局限性分析,其原因可能(但不完全)包含:1)该方法假设在局部热平衡(=)情况下,蒸散发等于平衡蒸发,未考虑平流项的影响。本研究发现公式(2)的第3 项数值极小,对估算结果几乎无影响。在灌溉农田站,第2 项所占数值比例也较低,该区域LE 低估主要是因为第1 项低估。也许NP 方法可以参考Priestley ‐ Taylor 公式加入一个系数,但这样又改变了无参数化方法的初衷。因此,可能需要进一步研究NP 方法与其他方法(如Priestley ‐ Taylor 公式、Penman-Monteith 公式)之间建立物理和数学上的联系。2)可能与输入数据和模型参数化中的错误有关,例如该方法使用代替了空气动力学阻力、表面阻力和土壤湿度的影响,这种空气动力学阻力和表面阻力的简化可能会削弱模型的性能。因为在不同生育期和作物类型表面阻力与的关系也许不是固定线性关系,同时在气象条件不稳定、下垫面变化剧烈(灌溉、作物收获等)情况下,这种替代关系可能并不总是适用。发展温差(−)与地表温度的线性关系可能是在不久的将来克服这一限制的一种可行方法。总的来说，由于所有输入参数少,且易获取/计算,NP 方法有可能成为一种常规监测地表热通量的方法; 利用常规卫星反演或者再分析资料,可能在大区域尺度甚至全球尺度提供一个蒸散发估算方法; 也有助于开发广泛应用于气象、水文、气候模式的陆面方案。目前,NP 方法用于其他下垫面类型(如城市混合下垫面、森林、湿地等)的适用性仍不明确,有待进一步研究。另外,NP 方法未来的研究将集中于计算方法、输入精度和残差的改进上。

5 结论

本文利用非参数化蒸散发估算方法估算了日尺度和30 min 尺度华北灌溉农田3 个典型站点的潜热通量,基于通量观测数据分析了该方法在不同季节及不同时间尺度的适用性,阐明了各输入参数的敏感性,探索了能量闭合修正对蒸散发估算结果验证的重要影响。研究主要结论:

1)非参数化估算方法在华北灌溉农田不同作物类型、不同时间尺度具有可靠和稳健的表现,可以较好地反映季节及日内变化特征,在日尺度和30 min 尺度上总体表现较好。在日尺度上NP 估算的LE (LE)与能量残差法修正后的涡度相关技术测定 的LE (LE)之 间 的Bias、RE、、RMSE 和NSE 分 别 为−16.18～−12.88 W·m、 20.6%～30.2%、0.80～0.83、22.45～31.06 W·m和0.66～0.75,在30 min尺度上分别为−13.30～−7.68 W·m、17.7%～24.8%、0.88、39.22～42.15 W·m和0.86～0.87。

2)非参数化估算方法在水分供应较充足时较严重低估潜热通量,而在较干燥时轻度低估或不低估潜热通量; 该方法对蒸散发对灌溉活动的响应考虑不足。从整体上看,非参数化估算方法在灌溉农田中普遍低估潜热通量,栾城、禹城和馆陶3 个站点年尺度上平均低估14.69 W∙m(RE:27.5%),30 min尺度上平均低估10.34 W∙m(RE:21.5%)。从作物类型上看,非参数化估算方法在玉米季(7−10月,供水以降水为主)估算精度高于小麦季(11月至次年6月,需大量灌溉补充降水的不足),3 个站点玉米生长季平均为0.80,小麦生长季平均为0.42。从生长周期上看,作物生长茂盛时,非参数化估算方法低估潜热通量,裸地或植被稀疏时几乎不再低估潜热通量,在栾城和禹城站6、7月份(裸地或作物稀疏)仅低估−1.38 W∙m,同时馆陶站(作物生长良好)低估−23.5 W∙m。

3)非参数化估算方法在华北灌溉农田中参数敏感性从高到低依次为、和和,日尺度上这4 个参数变化5%时的敏感性系数分别为11.3%、−10.4%、6.0%和−0.24%; 30 min 尺度上这4 个参数变化5%时的敏感性系数分别为11.75%、−10.94%、6.24%和−0.38%。

4) Bowen 比修正方法和能量残差修正方法可显著提高非参数估算方法模拟的一致性，其中可分别提高0.23 和0.25,RMSE 可分别降 低6.61 W·m和5.91 W·m,NSE 可分别提高0.27 和0.29。