基于人工鱼群优化BP 神经网络的光伏功率预测算法
王政宇,王胜辉,李潇潇,赵 音,田 巍
(1.沈阳工程学院 电力学院,辽宁 沈阳 110136;2.辽宁能源投资(集团)有限责任公司新能源发展部,辽宁 沈阳 110000;3.辽宁太阳能研究应用有限公司a.研发部;b.工程部,辽宁 沈阳 110136)
随着光伏并网数量的不断增加,对电网产生的冲击也逐渐增大[1-2]。为了提高电网接纳光伏的能力,弥补光伏出力不稳定的缺点,改善电网安全运行的稳定性,提出了光伏功率预测方法。功率预测方法可分为统计方法和物理方法,统计方法有采用多元线性回归模型预测技术法[3]、基于模糊C 均值聚类的光伏发电量预测法[4]等;物理方法有粒子群算法离线优化预测模型法[5]、ARMA自回归滑动模型与ARIMA 差分自回归移动模型相结合的光伏发电预测模型法[6]等。按预测方法又可分为直接预测方法和间接预测方法,直接预测有基于历史功率数据和简单日模型估计的神经网络预测方法[7]、基于历史功率数据和简单日模型估计的SVM 模型预测方法[8]等;间接预测方法有基于KPCA 与混合蛙跳算法的光伏电站发电量预测方法[9]、基于数据挖掘的光伏发电量预测方法[10]等。寻优算法与神经网络结合的方法也是较为有效的光伏功率预测方法,如基于混合灰色关联分析-广义回归神经网络的光伏电站短期功率预测方法[11]、基于思维进化算法和BP 神经网络算法的预测方法[12]、基于遗传算法优化小波神经网络的短期光伏功率预测方法[13]等。
人工鱼群算法(Artificial Fish-Swarm Algo‐rithm,简称AFSA)是有效的智能仿真寻优方法,有较强的鲁棒性和易与其他方法结合等优点[14]。因此,本文将基于人工鱼群算法与BP神经网结合,利用人工鱼群算法优化神经网络的权值和阈值,弥补了神经网络对初始值敏感、收敛速度慢等不足。
1 人工鱼群算法
人工鱼群算法是一种模仿水中鱼群的一些生存状态而创造出的一种仿生寻优算法。这种人工仿生算法利用了鱼群的觅食、聚群和追尾等行为,通过单个鱼的个体局部寻优,最终达到全局最优的目的。这种算法具有并行性、简单性、全局性、快速性和跟踪性等特点。人工鱼群算法不但对初始值不敏感,而且可有效避免陷入局部最优。另外,其兼容性很好,可以与其他算法结合使用。
1.1 人工鱼群算法原理
设一个生态环境中有n条人工鱼,人工鱼的个体状态可以表示为X=[x1,x2,x3,…,xn],其中xi为第i个人工鱼的状态,也就是寻优问题中的自由变量;环境中食物浓度为Y=f(X),即目标函数值;人工鱼i、j之间的距离为dij=ǁXi-Xjǁ;人工鱼的搜索半径为Visual;游动的步长为Step;拥挤度因子为δ。某一时刻第i个人工鱼xi在视野Visual内搜索到任意位置xj,若xj位置状态优于xi位置,则向xj位置方向前进一步,即到达xnext位置;否则,继续搜索视野范围内的其他位置,此过程可表示为

式中,Rand()为0~1之间的随机数。
在行动之前,每条人工鱼都会从觅食行为、聚群行为、追尾行为和随机行为中选择最优的执行,使鱼群能够到达食物浓度更高的位置。
1.2 人工鱼群基本行为
1)觅食行为
以求最大值为例,假设第i条人工鱼的某一时刻状态为Xi,在其搜索范围内随机选择一个状态Xj,满足公式(3)。

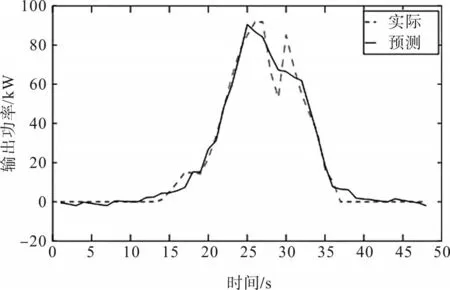
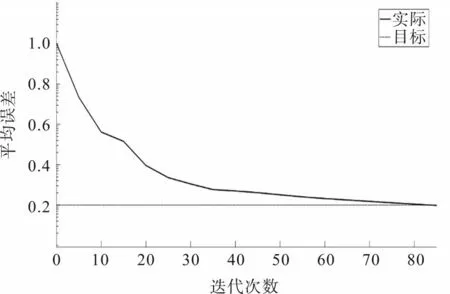
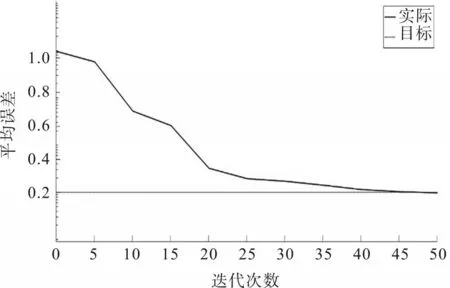
Yi和Yj分别表示Xi和Xj状态下的食物浓度。如果Yi 如果不满足前进条件,则重新在搜索范围内选择一个状态,判断是否满足移动的条件。反复选择Try number(设定的重复次数)次之后,如果仍然没有移动,则随机移动一步。 2)聚集行为 假设第i条人工鱼的某一时刻状态为Xi,在当前状态下搜索到同伴的数量为n,中心位置为Xc,判断依据为 式中,δ为拥挤度因子;Yc和Yi分别表示中心位置和当前位置的食物浓度。 如果式(5)成立,表示中心食物浓度较高且不拥挤,则向中心方向移动一步;如果不成立,则执行觅食行为。 3)追尾行为 假设第i条人工鱼的某一时刻状态为Xi,在当前状态下搜索附近同伴,找到同伴中食物浓度最大的Yj,其位置为Xj,判断依据为 如果式(6)成立,表明同伴Xj处具有浓度较高的食物并且不太拥挤,则向同伴Xj方向移动一步;如果不成立,则执行觅食行为。 4)随机行为 该行为是觅食行为的一个缺省行为,即在视野范围内随机选择一个位置向其移动,下一个状态的位置为 基于人工鱼群算法优化BP神经网络的主要思想: 1)利用人工鱼算法使BP神经网络的初始阈值和权值在最优值附近。其中,目标函数的值对应的是阈值和权值,即欲寻优的变量;每条人工鱼代表一个神经网络;食物浓度为神经网络误差的倒数。这样会使BP 神经网络的阈值和权值不再是随机的,避免了BP网络陷入局部最优值的问题。 2)将得到的权值和阈值用在BP神经网络中。 3)训练神经网络使其输出精度到达期望值。 本文采用此方法预测光伏功率,以下均以光伏功率预测为例。想要运用此方法解决问题,首先要确定神经网络模型。据相关文献记载,影响光伏输出功率的因素有很多,包括辐照度、温度、云量、太阳入射角和时间等。因为一些因素很难精确预测出,且对光伏的输出功率影响较小,所以本文只选择一些主要影响因素作为BP神经网络的输入。输入层神经元为3 个,输出层的神经元为1 个。对于隐含层和隐含层中神经元的个数的选择目前还没有明确的规定。本文采用Kolmogorov定理确定隐 含层神经元个数: 式中,s为隐含层神经元数;n为输入层神经元数。 这里的隐含层选择一层,隐含层中神经元的个数根据经验公式计算出为7 个,网络结构如图1所示。 图1 网络结构 图1中W为输入层和隐含层之间的权值;V为隐含层和输出层之间的权值;a和b分别为隐含层和输出层的阈值。BP神经网络样本训练的本质就是调节以上几个参数,使输出达到期望值。因此,将这些参数设置为人工鱼的状态,则人工鱼可以表示为 式中,w11、w12、w13为输入层到隐含层第1 个神经元的权值;a1为隐含层第1 个神经元的阈值;w1n,...,wmn为输入层神经元到隐含层第n个神经元的权值;an为隐含层第n个神经元的阈值;v11、v21、v31、v41为隐含层神经元到输出层第1 个神经元的权值;b1为输出层第1 个神经元的阈值;v1k,…,vnk为隐含层各个神经元到输出层第k个神经元的权值;bk为输出层第k个神经元的阈值。 人工鱼群算法在默认情况下寻求最大值。因此,水域中食物的浓度设置为BP 神经网络总误差的倒数。这样,人工鱼群算法求出的最大值对应的就是误差的最小值。任意人工鱼xz和xc之间的欧式距离可以表示为 基于人工鱼群优化神经网络的光伏功率预测大致分为4个部分:BP神经网络结构设计,人工鱼群算法优化BP神经网络,训练BP神经网络和BP神经网络光伏功率预测。其中,人工鱼群算法优化BP神经网络的过程就是利用人工鱼群算法寻找最优的权值和阈值的过程。光伏功率预测具体步骤如下: 步骤1:根据影响光伏输出功率的因素和需要输出的结果确定输入层和输出层神经元数量;根据经验公式确定隐含层数量和隐含层中神经元的数量,即设计BP神经网络结构。 步骤2:把BP 神经网络中的权值和阈值设定为人工鱼群算法中鱼群的寻优变量,BP 网络中误差的倒数用目标函数值表示,并对鱼群初始化。 步骤3:设定人工鱼群算法中的参数,包括步长、视野、最大迭代次数等。 步骤4:运行人工鱼群算法,算法结束后找出最小误差对应的权值和阈值。 步骤5:将权值和阈值赋给BP 神经网络作为其初始值。 步骤6:用历史数据训练神经网络,用训练成熟的BP神经网络对光伏输出功率进行预测。 为验证算法的有效性,本文采用MATLAB 软件构建预测光伏输出功率的BP 神经网络,将优化后的神经网络和没有优化的神经网络进行拟合实验并作对比。仿真中的BP神经网络是根据前文设计的光伏功率预测神经网络搭建的。网络中的输入层的神经元数量为3 个,分别表示太阳辐照度、环境温度和时间;输出层神经元数量为1 个,表示预测光伏的功率输出;隐含层神经元数量根据经验选择7个。 1)验证预测精度 设定BP神经网络中的相关参数:最大训练次数为100次,学习率为0.1。设定人工鱼群算法中的相关参数:最大迭代次数为100 次,人工鱼数量为20条,步长为0.7,视野范围为10,尝试次数为5。 无优化的BP 神经网络仿真结果如图2 所示。图中为实际输出和预测输出的曲线对比图,虚线为实际的功率输出,实线为预测的功率输出。从图中可以看出,没有经过优化的BP 神经网络的预测效果大致符合实际功率输出趋势,但在功率波动较频繁的时刻,预测的输出值存在很大的偏差。 图2 无优化BP神经网络实际输出和预测输出的曲线对比 优化后的BP 神经网络仿真结果如图3 所示。将优化后的实际和预测功率输出对比图与优化前的相比较,可以看出优化后的BP 神经网络预测的功率输出曲线更加接近实际的功率输出曲线,在功率变化较大的25 s~30 s 和30 s~35 s 时,无优化BP 神经网络预测精度平均误差为17.62% 和23.17%,优化后的BP 神经网络在上述时间段的平均误差分别为10.4%和13.41%,表明优化后的BP 神经网络比无优化的预测结果更准确、更加贴近实际值。 图3 优化后BP神经网络实际输出和预测输出的曲线对比 2)验证预测速度 设定BP 神经网络中的相关参数:目标精度为0.2,学习率为0.1。设定人工鱼群算法中的相关参数:目标精度为0.1,人工鱼数量为20 条,步长为0.7,视野范围为10,尝试次数为5。 无优化的BP 神经网络误差如图4 所示。该算法精度趋近0.2 时,迭代了约80 次。前期的误差逼近速度很快,但随着误差值接近目标值,速度也逐步减慢。 图4 无优化的BP神经网络误差 优化后的BP 神经网络误差如图5 所示。改进后的算法精度趋近0.2 时,迭代了约45 次。虽然前期误差逼近速度较改进前慢,但随着误差值接近目标值,速度也逐步加快。由此可知,在设定相同精度的情况下,无优化的BP 神经网络功率预测算法需要迭代80 次可达到设定的精度值,优化后的BP神经网络功率预测算法需要迭代45 次可达到设定的精度值,算法速度得到提升。 图5 优化后的BP神经网络误差 本文提出一种基于人工鱼群算法优化BP神经网络的光伏功率预测方法。此方法利用人工鱼群算法优化BP神经网络,可以解决BP神经网络易陷入局部最优值、收敛速度慢、对初始值敏感等问题,有效地提高了网络的稳定性和准确性。通过MATLAB仿真分析,得到如下结论: 1)只考虑辐照度、温度、时间对光伏功率输出影响的前提下,无优化的BP 神经网络在功率变化较大的25 s~30 s 和30 s~35 s 时,预测精度平均误差为17.62%和23.17%,均有所上升,证明没有优化的算法易受数据大波动的影响;而优化后的BP神经网络在上述时间段的平均误差分别为10.47%和13.41%,有效地提高了预测的精度。 2)只考虑辐照度、温度、时间对光伏功率输出影响的前提下,设定相同的精度值,无优化的BP神经网络在迭代80 次时达到设定的精度目标,而优化后的BP 神经网络在迭代45 次时就达到设定的精度目标。 3)基于人工鱼群优化BP神经网络的光伏功率预测算法能够有效地提高精度和速度。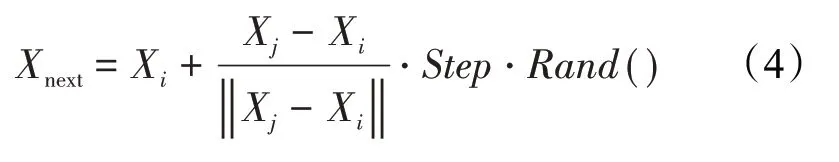



2 基于人工鱼群优化BP神经网络的光伏功率预测方法



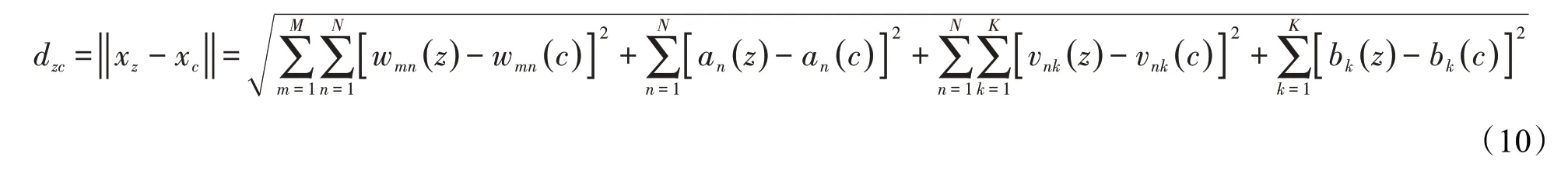
3 仿真计算

4 结论

