基于ABAQUS镀铝碳纤维编织格栅的拉伸性能

刘站 李晶 彭镇

摘 要：为探究镀铝碳纤维平纹编织格栅在大变形条件下的力学行为，采用试验与有限元模拟结合的方法，按照国标GB/T 1447—2005《纤维增强塑料拉伸性能试验方法》使用电子万能试验机对格栅试样进行拉伸性能测试;在Pro/E中建立格栅试样单胞模型，并导入有限元软件ABAQUS中对其进行拉伸模拟，通过试验数据验证仿真分析的有效性。结果表明：镀铝碳纤维平纹编织格栅具有高度非线性;经纬纱交织处容易产生应力集中，最易发生破坏失效;试验数值曲线与仿真数值曲线上升趋势一致且相差较小，验证了格栅模型仿真分析是可行的，为镀铝碳纤维编织格栅的设计及工程应用提供参考。

关键词：镀铝碳纤维编织格栅;拉伸性能;ABAQUS;应力位移

中图分类号：TB332

文献标志码：A

文章编号：1009-265X（2022）01-0047-07

Abstract： In order to investigate the mechanical behavior of aluminized carbon fiber plain braided grid under the condition of large deformation， the tensile properties of the grid sample were tested by electronic universal testing machine through the method of experiment combined with finite element simulation according to GB/T 1447-2005 Fiber-reinforced plastics composites-Determination of tensile properties. A unit cell model of the grid sample was established in Pro/E and imported into the finite element software ABAQUS for the subsequent tensile simulation. The validity of the simulation analysis was verified by the test data. The results show that the aluminized carbon fiber plain braided grid is highly nonlinear. The intersections of warp and weft yarns are prone to stress concentration and even destruction and failure. The experimental numerical curve exhibited an upward trend， which was consistent with the simulation numerical curve， and the difference is small. Thus， the feasibility of the simulation analysis of the grid model was verified， providing reference for the design and engineering application of aluminized carbon fiber braided grid.

Key words： aluminized carbon fiber braided grid; tensile properties; ABAQUS; stress- displacement

碳纖维是一种含碳量高于95%的特种纤维材料，因其具有质量轻、强度高等优点，常作为金属基、树脂基等复合材料的增强体使用，目前已广泛应用于汽车工业、航空航天、交通及医疗等领域[1]。金属基碳纤维材料既具有金属的良好塑性和韧性，同时兼备碳纤维的优异力学性能，一直是当前材料领域研究的热点。在高温状态下，金属容易与碳纤维生成金属碳化物，使得材料的性能降低，因此多选熔点较低的金属作为复合材料的基体，如铝/铝合金、镁、铜等，其中铝/铝合金具有较好的延展性、低密度，以及对纤维填充结合的蠕变成型能力强等优点，使得铝/铝合金在发展复合材料中备受青睐。与传统树脂基碳纤维相比，铝基碳纤维复合材料具有耐高温、防辐射、导电性能好等优点。当前军工装备等尖端领域的特殊性，对材料的功能要求更为苛刻，因此开发高性能材料并投入使用迫在眉睫，这也为铝基碳纤维复合材料的发展注入了强劲动力，这也显示出这类材料的巨大应用潜力。镀铝碳纤维是以金属铝为基体，连续碳纤维为增强体，经电镀后使得金属铝附着在碳纤维丝束表面，是铝基碳纤维复合材料的其中一种形式，镀铝碳纤维编织格栅是在镀铝碳纤维丝束的基础上，经编织后得到的结构形式，对其力学性能及应用进行探究具有一定的现实意义。目前，涉及碳纤维的研究多见于层合板与织物形式。因此，探究镀铝碳纤维编织格栅在大变形条件下的力学行为，具有一定的理论意义和实际应用价值。

相较于平纹织物，平纹编织格栅在结构上最大的区别在于经纬纱密度较少，且碳纤维复合材料多见于织物形式。因此，在对编织格栅拉伸研究中，可以借鉴织物的拉伸研究方法。目前，已有的研究探讨了碳纤维编织织物单轴拉伸性能，通过编织角度对比分析了其力学性能[2]。随着计算机技术的发展，仿真辅助工具被越来越多地应用在织物的性能预测中，刘倩楠等[3]提出一种评价和预测机织物拉伸性能的方法，通过模拟仿真与织物拉伸实验对比，验证数值模拟结果的有效性;李瑛慧等[4]基于织物周期边界条件理论和纱线拉伸试验，仿真模拟分析了三原织物的拉伸性能。针对不同种类的增强纤维织物，也有学者对其拉伸性能进行了研究，敬凌霄等[5]对增强纱以及涤纶双轴向经编织物和四轴向经编织物各纤维方向进行拉伸性能测试，分析了增强纱拉伸断裂强力和断裂伸长、双轴向和四轴向经编织物拉伸过程中的平均载荷-位移关系曲线，以及织物中的纱线强力利用率。李婉婉等[6]以玄武岩纤维、碳纤维为原料，设计出5种不同混杂比的三维正交织物，利用真空辅助成型工艺制备了乙烯基酯树脂基混杂复合材料，对其拉伸性能进行了测试，重点分析玄武岩纤维在织物中所占比例对复合材料拉伸性能的影响。蒋诗才等[7]制备了一种新型碳纤维复合材料格栅结构，通过试验研究了格栅结构单胞边长以及结构高度对格栅结构吸波/承载的影响，并测试了格栅结构的力学性能。张尉博等[8]通过数值模拟方法，探究格栅结构参数对型面热变形的影响程度。单庆布等[9]分析归纳了碳纤维复合材料格栅结构与金属材料格栅结构传热影响因素与规律。材料拉伸性能是材料最基础的力学性能，反映碳纤维复合材料格栅拉伸性能的研究较少。当前，镀铝碳纤维生产制备工艺复杂，对设备和环境要求严格，是造成镀铝碳纤维的研究较少的原因之一。

本文以T300-3K镀铝碳纤维平纹编织格栅为研究对象，按照國标GB/T 1447—2005《纤维增强塑料拉伸性能试验方法》使用电子万能试验机对镀铝碳纤维平纹编织格栅试样进行拉伸性能测试，通过仿真与试验对比，旨在探究镀铝碳纤维平纹编织格栅在大变形条件下的力学行为，对比实验与仿真结果验证有限元理论数值分析的可行性。

1 实 验

1.1 材料与设备

图1所示为镀铝碳纤维丝束。T300-3K碳纤维（台湾地区台丽公司），单丝直径7 μm;镀铝碳纤维丝束（威海展鹏公司），镀铝碳纤维实际生产工艺中的缺陷和误差在可接受范围内，其中铝体积分数为7%，碳纤维体积分数93%。

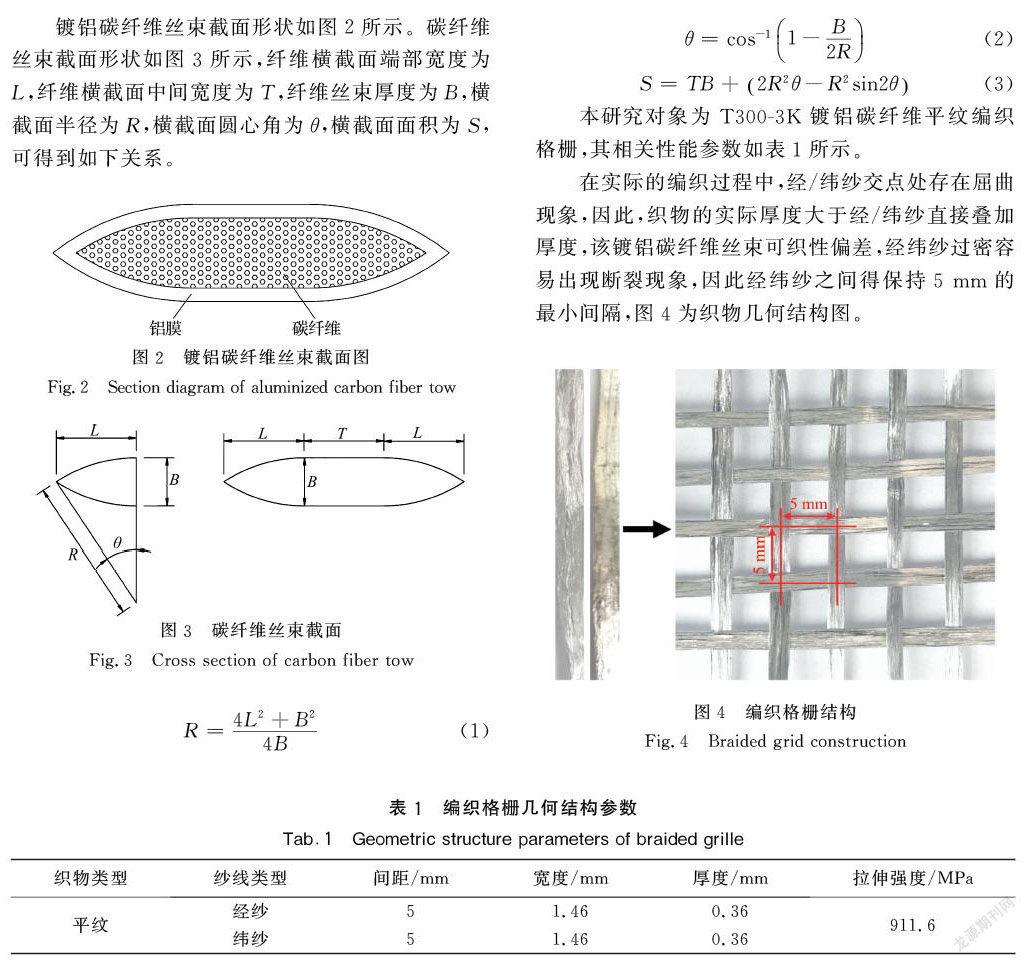
镀铝碳纤维丝束截面形状如图2所示。碳纤维丝束截面形状如图3所示，纤维横截面端部宽度为L，纤维横截面中间宽度为T，纤维丝束厚度为B，横截面半径为R，横截面圆心角为θ，横截面面积为S，可得到如下关系。

R=4L2+B24B（1）

θ=cos-11-B2R（2）

S=TB+2R2θ-R2sin2θ（3）

本研究对象为T300-3K镀铝碳纤维平纹编织格栅，其相关性能参数如表1所示。

在实际的编织过程中，经/纬纱交点处存在屈曲现象，因此，织物的实际厚度大于经/纬纱直接叠加厚度，该镀铝碳纤维丝束可织性偏差，经纬纱过密容易出现断裂现象，因此经纬纱之间得保持5 mm的最小间隔，图4为织物几何结构图。

1.2 试验方案

按照国标GB/T1447—2005《纤维增强塑料拉伸性能试验方法》使用UTM5205X，200 kN微机控制电子万能试验机对镀铝碳纤维平纹编织格栅试样进行拉伸性能测试。除去夹持所需长度，试样有效尺寸为150 mm×30 mm。试验时，沿格栅纵向进行拉伸，纵向为经纱方向，横向为纬纱方向，拉伸速度为2 mm/min。为了加大试样与夹具之间的摩擦力防止出现滑脱现象，加强片区域采用0.5 mm厚的牛皮纸包裹。试样宽度满足夹具夹持条件，装夹时使试样纵向与夹具上下夹头的加载轴线重合，确保实验台固连的夹具处于完全固定状态。试验条件设定为：常温状态下，等速伸长（CRE），上下夹具间隔150 mm，取5组合格试样进行分析，输出格栅拉伸实验力-位移曲线，拉伸示意如图5所示。

2 格栅拉伸有限元模拟

2.1 模型建立

平纹编织格栅在平面内其结构形式具有周期性，为简化分析，提高计算速度，可取其最小可重复结构即单胞模型开展研究[10]。在Pro/E中，对镀铝碳纤维编织格栅结构化建模，镀铝碳纤维平纹编织格栅单胞模型如图6所示。碳纤维及铝膜基本力学参数如表2所示。

2.2 有限元模拟

ABAQUS是一款功能强大的工程模拟有限元软件，它既可以分析复杂的结构力学问题，又能求解复杂的非线性问题[11]。

为确保单胞模型能够表征试样的整体性能，需要对编织格栅单胞施加周期性边界条件。依据Whitcomb等[12]和Xia等[13]提出的周期性边界条件理论，推导出格栅单胞拉伸所需周期性边界条件公式。图7为格栅单胞坐标示意图，其中w=6.5 mm（沿y轴方向单胞长度），l=6.5 mm（沿x轴方向单胞长度），h=1.34 mm（沿z轴方向单胞长度），A、B、C、D、E、F、G、I为单胞顶点处的节点。

为了消除单胞刚体位移，约束坐标原点A以及沿x、y、z 3个方向B、D、E顶点的自由度。表达式如下：

UxA=UyA=UzA=0

UxB=UyE=UzD=0（4）

式中：Ux、Uy、Uz表示为沿x、y、z方向的位移;A、B、E、D对应单胞顶点处的节点。

二维编织复合材料周期性边界条件公式为

U（k+）i-U（k-）i=εijΔx（k）j=cji（5）

式中：U（）i为边界上周期位移修正量;i、j（i=1，2，3;j=1，2，3）分别为坐标的3个方向;k+、k-分别表示法向沿坐标轴正负2个方向的周期性边界面;εij为单胞平均应变;Δx（k）j为单胞内任意2个点的坐标位移差;cji为常量。推导出单胞面上节点周期性边界条件如下。

法向沿x轴

Uxx=l-Uxx=0=0-UxD=0

Uyx=l-Uyx=0=0-UyD=0

Uzx=l-Uzx=0=0-UzD=0（6）

法向沿y轴

Uxy=w-Uxy=0=0-UxB=0

Uyy=w-Uyy=0=0-UyB=0

Uzy=w-Uzy=0=0-UzB=0（7）

式中：Ux、Uy、Uz表示为沿x、y、z方向的位移;B、D为对应单胞顶点处的节点;下标等式表示对应面上的节点。格栅试样在沿z轴方向上，其结构不具有周期性，因此，法向沿z轴的面不需要施加周期边界约束。同时，还需施加棱边节点约束以及顶点约束，其周期性边界条件推导与面上节点约束原理相同。结合单胞结构几何参数，在ABAQUS中对单胞施加周期性边界条件，建立位移约束方程。

在分析计算阶段，本研究使用显示求解器模块ABAQUS/Explicit进行计算。格栅的经/纬纱结构由铝膜和碳纤维组成，经/纬纱横截面近似椭圆形，采用扫略中性轴算法并定义扫略路径，经/纬纱模型结构中的铝膜和碳纤维均采用六面体单元进行网格划分。织物经/纬纱有限元模型如图8所示。

由于实际的镀铝碳纤维丝束表面及内部存在部分缺陷，在创建拉伸模拟时，作出以下假设：a）将镀铝碳纤维丝束表面、纤维内部看作均匀实体且丝束处于完全平直状态。b）镀铝碳纤维丝束截面为椭圆形，丝束与铝膜完全结合，因此设置碳纤维丝束与基体铝膜为Tie约束。定义经纱与纬纱之间的切向摩擦系数为0.17，经纱与纬纱之间的接触算法为“all with self”。在格栅经纱截面一端建立参考点RP-1，设置参考点RP-1与织物经纱截面为MPC耦合约束，在参考点RP-1上施加拉伸速度2 mm/min。

3 结果与讨论

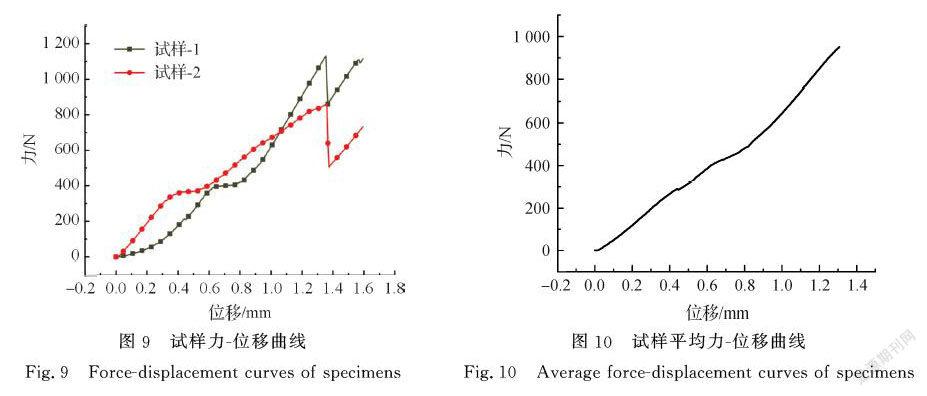
表3所示为试样拉伸破壞载荷。在实际拉伸过程中，输出的力-位移曲线非线性明显，数值波动较大。从五组试验数据中取上升趋势较好且数值较稳定的两组试验数据，输出格栅拉伸试验力-位移曲线，如图9所示。由图9可知镀铝碳纤维编织格栅在拉伸试验中波动性较大，其力-位移曲线具有高度非线性，这是由于试件在拉伸过程中，经纱中纤维断裂不一致造成的。当拉伸位移达到1.3 mm后，经纱出现大量断裂现象。因此，为保证数据的准确性取1.3 mm以内的力-位移曲线为参考。为了更准确反应格栅拉伸响应，将试样-1、试样-2的力-位移数据取平均值拟合为曲线，如图10所示。

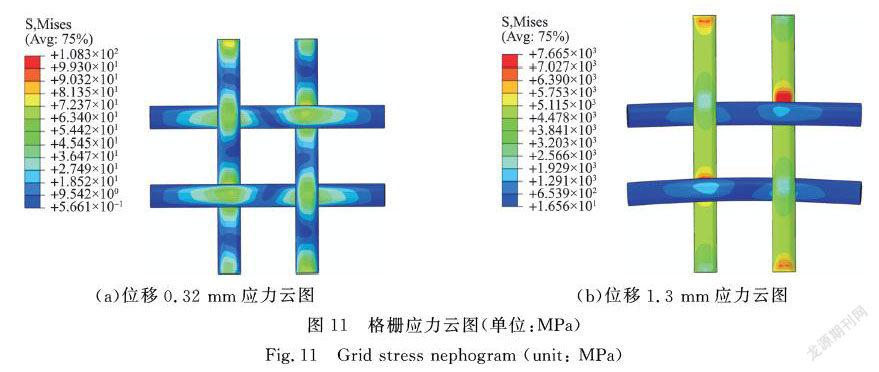
由图9可知，位移在0到1.3 mm之间时，力-位移之间表现出较好的线性关系;位移达到1.3 mm时，格栅拉伸开始出现较大的波动性。在有限元模拟中，选取位移在0到1.3 mm之间的数据，并与试验数据进行对比。经ABAQUS分析计算，单胞模型拉伸应力分布云图如图11所示。经/纬纱交织点处所受应力最大。通过观察试件实际拉伸过程，经纱在拉力作用下由屈曲状态逐渐伸直，由于本研究模拟的是纵向（即径向）拉伸，经纱承受主要拉力，因此其应力分布明显。在应力云图中可以明显地看到，经纱纬纱通过交织点相互接触实现力的传递，由于交织点处摩擦力的作用，使得纬纱产生滑移和形变，容易产生应力集中，最易发生破坏失效，这与实际试验相符。

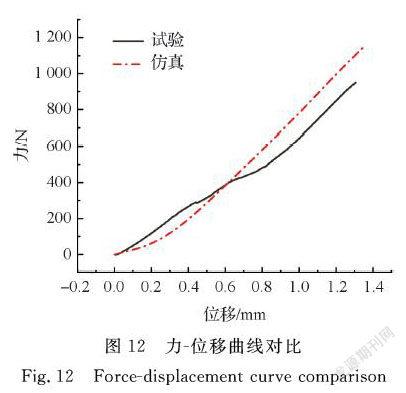
通过ABAQUS对单胞试件拉伸性能的模拟，得到应力-位移数值曲线，并与试样平均数值曲线进行对比，如图12所示。由试验数值曲线可知，位移在0～0.4 mm时，应力和弹性模量相对较小，这是由于屈曲的经纱逐渐被拉直造成的;位移在0.4～0.8 mm时，试验数值曲线出现了拐点;位移在0.8～1.3mm时，试件进入弹性阶段，纱线所受应力呈线性增长。因此，该试件的拉伸实验能够表征出镀铝碳纤维平纹编织格栅的力学特性。由仿真数值曲线与试验数值曲线对比可知，仿真数值曲线与实验数值曲线上升趋势较吻合，存在的误差在可接受范围内，能较准确地反映出格栅拉伸力学响应。

4 结 论

以T300-3K镀铝碳纤维平纹编织格栅为研究对象，结合拉伸试验与仿真分析方法，探讨了镀铝碳纤维编织格栅的力学性能，主要研究结论如下：

a）通过试验测定的试件拉伸性能数据能够表征出镀铝碳纤维平纹编织格栅的力学特性。试验数值曲线与仿真数值曲线上升趋势具有较好的一致性，证明有限元分析的可行性，为镀铝碳纤维平纹编织格栅的设计及工程应用提供参考。

b）由试验数值曲线可知镀铝碳纤维编织格栅在拉伸试验中波动性很大，其力-位移曲线具有高度非线性。

c）由格栅应力云图可知，经纬纱交织处最易产生应力集中发生失效破坏，且应力演变云图与实际相符。

由于碳纤维属于各向异性材料，其复合材料的力学响应较为复杂，在今后的研究中对镀铝碳纤维的损伤效应将进一步展开分析。

参考文献：

[1]刘万双，魏毅，余木火.汽车轻量化用碳纤维复合材料国内外应用现状[J].纺织导报，2016（5）：48-52.

LIU Wanshuang， WEI Yi， YU Muhuo. Current situations of carbon fiber reinforced composites used for lightweighting of automobile at home and abroad[J]. China Textile Leader， 2016（5）： 48-52.

[2]BORIS D， XAVIER L， DAMIEN S. The tensile behaviour of biaxial and triaxial braided fabrics[J]. Journal of Industrial Textiles， 2016， 47（8）：2184-2204.

[3]刘倩楠，张涵，刘新金，等.基于ABAQUS的三原组织机织物拉伸力学性能模拟[J].纺织学报，2019，40（4）：44-50.

LIU Qiannan， ZHANG Han， LIU Xinjin， et al. Simulation on tensile mechanical properties of three-elementary weave woven fabrics based on ABAQUS[J]. Journal of Textile Research， 2019， 40（4）： 44-50.

[4]李瑛慧，谢春萍，刘新金.三原组织织物拉伸力学性能有限元仿真[J].纺织学报，2017，38（11）：41-47.

Li Yinghui， XIE Chunping， LIU Xinjin. Finite element simulation on tensile mechanical properties of three-elementary weave fabric[J]. Journal of Textile Research， 2017， 38（11）： 41-47.

[5]敬凌霄，何婷婷，陈星安，等.涤纶多轴向经编织物拉伸性能研究[J].针织工业，2017（12）：58-60.

Jing Lingxiao， HE Tingting， CHEN Xingan， et al. Study of tensile properties of multi-axial war p-knitted polyester fabrics[J]. Knitting Industries， 2017（12）： 58-60.

[6]李婉婉，汪进前，盖燕芳，等.玄武岩/碳纤维混杂三维正交复合材料拉伸性能研究[J].现代纺织技术，2019，27（2）：1-5.

LI Wanwan， WANG Jinqian， GAI Yanfang， et al. Investigation on tensile properties of three-dimensional orthogonal basalt/carbon fiber hybrid composite[J]. Advanced Textile Technology， 2019， 27（2）： 1-5.

[7]蒋诗才，石峰晖.碳纤维复合材料格栅结构的吸波/承载性能研究[J].舰船电子工程，2019，39（3）：82-86.

JIANG Shicai， SHI Fenghui. Study on microwave-absorbing and mechanical properties of advanced stiffened grid structure for carbon fiber[J]. Ship Electronic Engineering，2019， 39（3）： 82-86.

[8]張尉博，张琦，徐宏涛，等.高稳定碳纤维格栅夹层反射器结构设计及型面热变形优化[J].复合材料科学与工程，2020（5）：40-46，62.

ZHANG Weibo， ZHANG Qi， XU Hongtao， et al. Structure design of carbon fiber grid sandwich reflector with high stability and optimization of thermal deformation[J]. Composites Science and Engineering， 2020（5）： 40-46+62.

[9]单庆布，张淑杰.碳纤维复合材料格栅横向传热影响因素分析[J].高科技纤维与应用，2019，44（1）：53-62.

SHAN Qingbu， ZHANG Shujie. Analysis of influencing factors on transverse heat transfer of carbon fiber composite grille[J]. Hi-Tech Fiber and Application，2019， 44（1）： 53-62.

[10]薛亚红，陈继刚，闫世程，等.二维机织复合材料力学分析中的周期性边界条件研究[J].纺织学报，2016，37（9）：70-77.

XUE Yahong， CHEN Jigang， YAN Shicheng， et al. Periodic boundary conditions for mechanical property analysis of 2-D woven fabric composite[J]. Journal of Textile Research， 2016， 37（9）： 70-77.

[11]靳欢欢.机织物三点梁弯曲性能有限元模拟与分析[D].上海：东华大学，2016.

JIN Huanhuan. Simulation and Analysis of Three-point Bending Property of Woven Fabrics by Finite Element Method[D]. Shanghai： Donghua University， 2016.

[12]WHITCOMB J D， CHAPMAN C D， TANG X D. Derivation of boundary conditions for micromechanics analyses of plain and satin weave composites[J]. Journal of Composite Materials， 2000， 34（9）：724-747.

[13]XIA Z， ZHOU C， YONG Q， et al. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites[J]. International Journal of Solids & Structures， 2006， 43（2）：266-278.