海洋双层管双梯度钻井井筒温度分布规律研究*
王江帅 付 盼 胡旭辉,3 宫臣兴 邓 嵩 唐 政 殷 文
(1.常州大学石油与天然气工程学院 2.中国石油集团工程技术研究院有限公司 3.西安康布尔石油技术发展有限公司 4.中国石油长庆油田油气工艺研究院 5.低渗透油气田勘探开发国家工程实验室)
0 引 言
为了有效解决深水钻井的窄密度窗口[1-6]和浅层水合物开采面临的地层漏失严重、开采效率低[7]等难题,西南石油大学能源装备研究院创新性提出了一种基于双层管双梯度的深海油气及水合物开发技术方案[8],并建立了该钻井方式下的井筒压力调控理论及策略。然而,该钻井方式下井筒流体物性参数变化、井筒压力计算[9-10]以及后续开采过程中水合物在双层管内是否发生分解、分解位置以及分解量等均受井筒温度的显著影响。因此,亟待开展海洋双层管双梯度钻井井筒温度场研究,以期为井筒压力的准确预测和保障水合物安全、高效的开采提供理论支撑。
现有的传热模型大多是用来预测正常循环[10-11]、漏失[12]、溢流[13]等不同工况下的井筒温度分布,这些模型针对的是“钻杆内流入、环空流出”这种井筒流动传热方式,适用于常规钻井方式。然而,双层管双梯度钻井过程中钻井液由外管环空注入,经钻头后与岩屑一起由内管返出。此外隔水管环空、套管环空、裸眼环空分别被海水、隔离液、钻井液3种不流动的流体充满[8]。由此可见,双层管双梯度钻井的井筒流动传热方式为“环空流入、钻杆内流出”,且不同井段环空流体类型差异较大,导致井筒-地层之间的传热非常复杂。现有的井筒温度场预测模型已不再适用。为此,笔者基于传热学理论,充分考虑岩屑对内管混合流体热物性参数的影响,以及隔水管、套管、裸眼等井段环空内不同流体类型对传热的影响,并将外管内壁至原始地温位置之间的区域,等效为一个传热单元,引入综合导热系数,建立了适用于双层管双梯度钻井的井筒温度场预测模型,并对井筒温度分布规律进行分析。
1 物理模型
双层管双梯度钻井井筒物理模型如图1所示。由图1可知,钻井过程中钻井液由外管环空注入,经钻头喷嘴后与岩屑一起由内管返出,环空被海水、隔离液、钻井液3种流体充满,并处于静止状态。在此过程中,地层与外管环空钻井液进行热交换,外管环空钻井液与内管混合流体进行热交换。

图1 双层管双梯度钻井井筒物理模型
2 数学模型
2.1 基本假设
在建立双层管井筒温度场数学模型时,进行以下假设:①内管和外管环空内流体温度在径向上不发生变化;②井筒中心线向外一定距离处地层温度为原始地温(C.S.HOLMES and S.C.SWIFT认为不受扰动的地层半径值为3.05 m[14],本文选取该值作为原始地温位置与井眼中心轴线的距离),同时将外管内壁至原始地温位置之间的区域等效为一个传热单元,引入综合导热系数;③热源项计算时,考虑由于井筒流体流动摩阻所产生的热量;④综合导热系数计算时,考虑海水、隔离液、钻井液等不同流体导热系数差异。
2.2 温度场模型
与常规钻井方式不同,双层管双梯度钻井流体从外管环空注入,经钻头后从内管返出。因此,基于热力学第一定律,分别针对外管环空和内管(见图2)2种流动传热区域内的流体建立热传导控制方程。
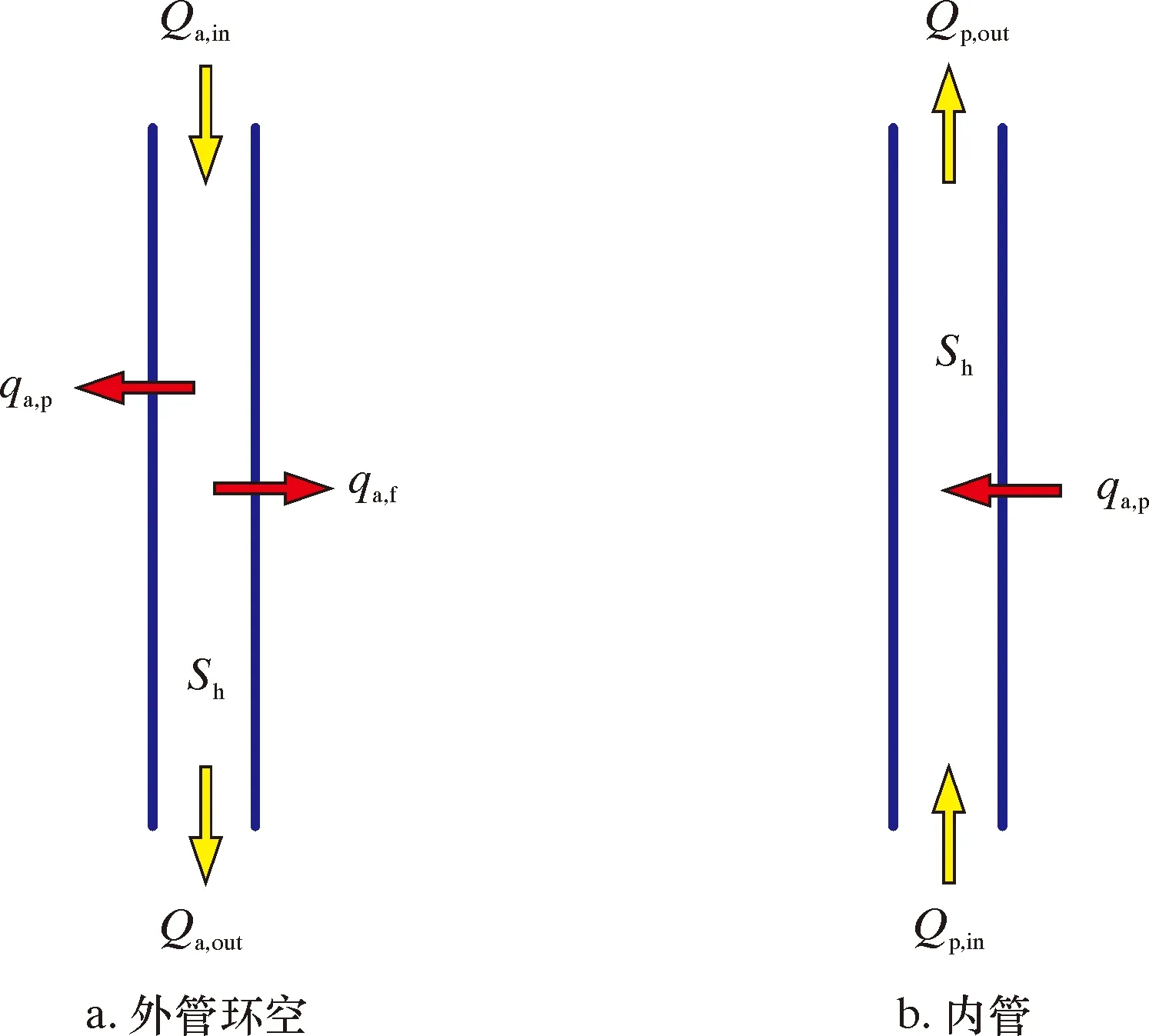
图2 双层管双梯度钻井井筒内流体传热示意图
2.2.1 外管环空流体
Qa,in-Qa,out-qa,p-qa,f+Sh=Qa,change
(1)
其中:
(2)
式中:Qa,in为流入外管环空控制体的流体热量,J;Qa,out为流出外管环空控制体的流体热量,J;qa,p为单位时间内外管环空流体向内管流体的导热量,J;qa,f为单位时间内外管环空流体向地层的导热量,J;Sh为由于流体流动时压耗所产生的热量,J;Qa,change为外管环空控制体流体热量的改变量,J;Ca为流入外管环空控制体流体的比热容,J/(kg·℃);qma为流入外管环空控制体的流体质量流量,kg/s;Ta,L为流入外管环空控制体的流体温度,℃;Ta,L+△L为流出外管环空控制体的流体温度,℃;Dp为内管外径,m;λp为双层管的导热系数,W/(m·℃);Da为原始地层温度位置处的圆柱外径,m;λwell为外管内壁至原始地层温度位置处传热体的综合导热系数,W/(m·℃);Twell为外管内壁至原始地层温度位置处的传热体温度,℃;Aa为外管环空流体流动的面积,m2;ρa为流入外管环空控制体的流体密度,kg/m3;Tp,L为控制体流入端对应的内管流体温度,℃;bp为内管的壁厚,m;Tg,L为控制体流入端对应的原始地层温度,℃;bwell为外管内壁至原始地层温度位置处的距离,m;ΔL为控制体的长度,m;Δt为时间步长,s。
代入控制方程,推导后得出外管环空流体温度计算方程:
(3)
其中:
(4)
2.2.2 内管流体
Qp,in-Qp,out+qa,p+Sh=Qp,change
(5)
其中:
(6)
式中:Qp,in为流入内管控制体的流体热量,J;Qp,out为流出内管控制体的流体热量,J;Qp,change为内管控制体流体热量的改变量,J;Cp为流入内管控制体流体的比热容,J/(kg·℃);qmp为流入内管控制体的流体质量流量,kg/s;Tp,L+ΔL为流入内管控制体的流体温度,℃;Ap为内管流体流动的面积,m2;ρp为流入内管控制体的流体密度,kg/m3。
代入控制方程,推导后得出内管流体温度计算方程:
(7)
其中:
B1=CpqmpΔt
B2=CpρpApΔL
(8)
2.3 辅助方程
2.3.1 热物性参数
由于钻井液从井底往上返出时有岩屑的进入,因此改变了内管混合流体的热物性参数。
混合流体密度:
(9)
混合流体的质量流量:
mp=ma+ms=ρaQl+ρsQs
(10)
混合流体的比热容:
(11)
式中:ρs为岩屑的密度,kg/m3;Ql为钻井液排量,m3/s;Qs为岩屑的产生速率,m3/s;Cs为岩屑的比热容,J/(kg·℃);mp为混合流体质量流量,kg/s;ma为返出流体质量流量,kg/s;ms为岩屑的质量流量,kg/s。
2.3.2 综合导热系数
由于建立数学模型时,将外管内壁与原始地温之间的区域视为一个传热单元,因此针对该传热单元引入综合导热系数λwell,计算公式如下:
(12)
式中:L为计算点的深度,m;Dwater为水深,m;Dshoe为套管鞋深度,m;ba1为外管壁厚,m;λsea为海水导热系数,W/(m·℃);ba2为隔水管段环空间隙,m;λriser为隔水管导热系数,W/(m·℃);briser为隔水管壁厚,m;λiso为隔离液导热系数,W/(m·℃);λcasing为套管导热系数,W/(m·℃);bcasing为套管壁厚,m;λcement为水泥环导热系数,W/(m·℃);bcement为水泥环壁厚,m;λf为地层导热系数,W/(m·℃);λd为钻井液导热系数,W/(m·℃)。
2.3.3 热源项计算
热源项[15]由下式计算:
(13)
式中:ΔPv为单位长度的摩阻压降,Pa/m;Ab为钻头喷嘴的截面积,m2;Eb为钻头破岩效率;M为轴向上的钻柱扭矩,N·m;ω为转速,r/s。
3 模型求解
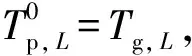
(14)
式中:D为井深,m;i为时间节点;j为空间节点;E为误差控制参数,无量纲。
4 实例分析
使用上述建立的数学模型,开展了双层管双梯度钻井井筒温度场数值模拟研究。模拟井为一口深水直井,基本参数包括:井深2 000 m,水深1 500 m,套管下深1 800 m,隔水管外径0.533 m,隔水管内径0.508 m,套管外径0.468 m,套管内径0.404 m,外管外径0.308 m,外管内径0.248 m,内管外径0.127 m,内管内径0.109 m,钻井液密度1 100 kg/m3,排量30 L/s,钻井液比热容3 180 J/(kg·℃),岩石密度2 650 kg/m3,岩石比热容920 J/(kg·℃),管柱导热系数43 W/(m·℃),岩石导热系数2.25 W/(m·℃),水泥环导热系数1.7 W/(m·℃),钻井液导热系数1 W/(m·℃),海水导热系数0.8 W/(m·℃),隔离液密度1 440 kg/m3,隔离液导热系数0.5 W/(m·℃),隔离液比热容1 840 J/(kg·℃),机械钻速2 m/h,注入流体温度30 ℃,海平面温度30 ℃,地温梯度0.028 ℃/m。
4.1 井筒温度分布规律
图3展示了双层管双梯度钻井时外管环空流体温度和内管流体温度分布情况。由图3可以看出:循环时钻井液以一定温度从外管环空注入,向下流动过程中受到海水温度场的影响,外管环空流体温度逐渐降低;进入泥线以下地层时,受地层温度场的影响,外管环空流体温度有所升高。总体来说,在井筒上部(即图3中①区域),热传导方向为外管环空流体→地层;在井筒下部(即图3中②区域),热传导方向为地层→外管环空流体。此外,外管环空流体经钻头后沿内管向上返出,该过程中内管流体受周围环境温度的影响在流动方向上呈现出先减小后增大的变化趋势。

图3 双层管双梯度钻井井筒温度分布
另外,结合双层管双梯度钻井进行水合物固态流化开采工艺,对井筒温度分布进行深入分析。由于受到海水温度场的影响,水合物固态流化开采时,在井下被破碎并分离后,沿内管向上流动过程中在海底泥线附近区域(低温高压环境)易形成结晶。一旦有水合物晶体形成,将会影响井筒流动,严重时会给井筒流动保障带来安全隐患。因此,建议优化相关可控参数来增大海底泥线附近井筒温度,避免因井筒温度过低而形成大量的水合物晶体。
4.2 不同因素对井筒温度分布的影响
4.2.1 注入流体温度
图4展示了3种不同注入流体温度条件下的内管流体温度分布情况。由图4可以看出,随着注入流体温度的升高,内管流体温度剖面整体增大。内管流体温度的升高有利于抑制水合物的生成,从而缩小水合物在井筒内的生成区域,保障井筒流动。
由图4还可以看出,井口附近内管流体温度受注入流体温度的影响较大,而海底、井底附近内管流体温度受注入流体温度的影响相对较小。具体来看,注入流体温度从20 ℃升高到40 ℃时,井口(0 m)温度升高了18.25 ℃,而海底(1 500 m)温度仅升高了1.48 ℃,井底(2 000 m)温度仅仅增加了1.02 ℃。这是因为,对于井口流体来说,内管流体温度受外管环空注入流体温度直接影响,然而对于井底来说,经过长时间循环后,井筒换热充分,因此注入流体温度对井底温度的影响非常有限。

图4 注入流体温度对井筒温度分布的影响
4.2.2 排量
图5展示了3种不同排量条件下的内管流体温度分布情况。由图5可以看出,随着排量的增加,内管流体温度剖面整体增大,有利于抑制水合物的生成,从而缩小水合物在井筒内的生成区域,保障井筒流动。与常规陆地钻井不同的是,对于深水浅部地层钻井,排量的增大并没有导致井底温度减小,反而使其增大。这是因为,排量越大井筒内流体与地层的换热时间越少,受深水海底和浅部地层低温的影响更小,故内管流体温度增加。
由图5还可以看出,海底附近内管流体温度受排量的影响较大,而井口、井底附近内管流体温度受排量的影响相对较小。具体来看,排量从20 L/s增加到40 L/s时,井深1 500 m处的海底温度升高了3.64 ℃,井底(2 000 m)温度升高了1.18 ℃,而井口(0 m)温度仅仅变化了0.27 ℃。也就是说,相比于井口、井底,排量的增加可以更有效地改善海底附近井筒内的低温环境,从而有效抑制水合物在海底附近的井筒内形成。

图5 排量对井筒温度分布的影响
4.2.3 钻井液比热容
图6展示了3种不同比热容钻井液在内管流体温度分布情况。由图6可以看出,随着钻井液比热容的增加,内管流体温度剖面整体增大,同样有利于抑制水合物的生成,从而缩小水合物在井筒内的生成区域,保障井筒流动性。这是因为,钻井液比热容越大,井筒内流体与流体之间的热对流增强越明显,相比于海底低温,注入流体温度较高,有利于内管流体温度增加。
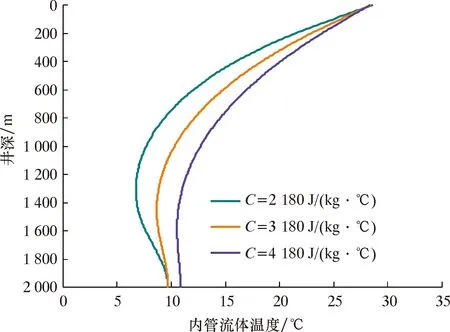
图6 钻井液比热容对井筒温度分布的影响
由图6还可以看出,海底附近内管流体温度受钻井液比热容的影响较大,而井口、井底附近内管流体温度受钻井液比热容的影响相对较小。具体来看,钻井液比热容从2 180 J/(kg·℃)增加到4 180 J/(kg·℃)时,井深1 500 m处的海底温度升高了3.45 ℃,井底(2 000 m)温度升高了1.13 ℃,而井口(0 m)温度仅仅变化了0.25 ℃。也就是说,相比于井口、井底,钻井液比热容的增加可以明显地改善海底附近井筒内的低温环境,对有效抑制水合物在海底附近的井筒内形成有一定的作用。
综上分析,可以得出以下3点认识:①对双层管双梯度钻井井筒而言,其在海底附近的温度达到最低值,在水合物固态流化开采时应注意增大海底附近井筒温度,避免因温度过低而形成大量的水合物晶体,从而阻碍井筒流动。②注入流体温度、排量和钻井液比热容的增大,均会使得内管流体温度剖面整体增大,是通过调节井筒温度剖面来抑制水合物生成的重要手段。③注入流体温度主要影响的是井口附近的内管流体温度,而排量和钻井液比热容主要影响的是海底附近的内管流体温度,可以通过调节上述参数来改善不同井段井筒温度分布,以减少水合物的生成。
5 结 论
(1)针对双层管双梯度钻井方式,充分考虑岩屑对内管混合流体热物性参数的影响以及隔水管、套管、裸眼等井段环空内不同流体类型对传热的影响,并将外管内壁至原始地温位置之间的区域等效为一个传热单元,引入综合导热系数,建立了该钻井方式下的井筒温度场预测模型。
(2)对双层管双梯度钻井井筒而言,其在海底附近的温度达到最低值,在水合物固态流化开采时应特别注意该段的井筒温度分布。
(3)注入流体温度、排量和钻井液比热容的增大,均会使得内管流体温度剖面整体增大;其中,注入流体温度主要影响的是井口附近的内管流体温度,而排量和钻井液比热容主要影响的是海底附近的内管流体温度,可以通过调节上述参数来改善不同井段井筒温度分布,以减少水合物的生成。

