修正的横观各向同性岩体强度破坏准则

张虎承

(深圳市水务工程检测有限公司,广东 深圳 518110)

1 概述

天然沉积环境下形成的层状岩石容易表现出横观各向同性，即沿某平面内的各方向力学性质相同，而垂直该面方向的弹性性质差异明显的现象。作为各向异性的一种特殊情况，横观各向同性对于岩体应力一应变特征以及破坏的力学行为有十分重要的影响，而传统的Mohr-Coulomb和Hoek-Brown等强度准则未能精确地，定量化地描述该特征。因此，有必要建立一套合适的强度理论对横观各向同性岩体的强度和破坏特征进行预测。目前，国内外学者对该问题展开了广泛的研究工作，Jaeger[1]考虑了层理面倾角对黏聚力的影响，对传统的岩体强度理论进行了完善；王洪新[2]通过引入各向异性影响因子等参数，更好地在强度准则中反映千枚岩的各向异性特征；田雨等[3]采用修正应力法，考虑各向异性对岩土材料抗剪强度影响，得到了修正的Mohr-Coulomb强度准则；施建俊等[4]以现场声波数据和模糊综合预测理论为依托，对Hoek-Brown强度准则的爆破扰动参数进行研究，更为可靠和准确的修正公式；高悦等[5]对修正系数Km和Ks进行了探讨，得到了更为准确的Hoek-Brown修正公式。

上述研究从各个角度对岩石破裂的强度准则进行了修正，使其更好地贴合工程实际，但并未能清晰及全面地对岩体的横观各向同性进行表征。为此，本文通过引入岩石体积节理比Jv，节理断续度Jc，岩体摩擦比系数Jf，节理平直度Js和节理弱化乘子γ5项指标，从多个维度考虑岩体的横观各向同性，对传统的Hoek-Brown强度破坏准则进行修正。

受技术条件所限，实际中定制化地预制节理(尤其是试样内部)具有一定的困难性，故本文选取数值计算求得的离散解进行理论模型的对比验证手段。虽然数值模拟并不能代替实际工程方法，但作为解决岩土工程问题的一种手段，颗粒离散元在岩石强度准则修正和模拟岩石破裂中具有其独特的优势[6-9]，已得到广泛的应用，不失为对实际工程的一种补充，也为岩土工程强度预测提供合理的依据。

2 修正的Hoek-Brown强度破坏准则

2.1 传统的Hoek-Brown强度破坏准则

经过国内外学者对Hoek-Brown 准则进行修正，得到了适用性更强的Hoek-Brown准则：

(1)

(2)

(3)

(4)

式中:

σ1、σ3——岩体破坏时最大、最小主应力;

σc——试件的单轴抗压强度;

mi——完整岩石的Hoek-Brown 常数;

m、s——与岩体软硬程度、破坏程度有关的常数;

GSI——岩体地质强度指标;

D——扰动系数。

对于Hoek-Brown 强度准则中参数，σc可以直接通过试验获取，而参数m、s的确定，由式(2)(3)(4)可知，来源于扰动系数D和岩体地质强度指标GSI。D是表征了岩体受扰动的程度，取值范围为0～1，完整岩块一般取为1，一般结合实际工程地质情况获取。而地质评分GSI的获取一般依托于工程经验或查表，定量化的取值一般较为困难，而岩体的横观各向同性性质隐含与GSI之中，因而需要表征岩体的横观各向同性，需要给出更加明确的GSI值。王新刚等[10]和胡盛文等[11]提出更加准确的GSI量化取值，但并未能全面地描述岩石的横观各向同性。为此，本文提出了针对横观各向同性岩体的Hoek-Brown 修正准则。

2.2 适用于横观各向同性岩体的Hoek-Brown强度破坏准则

为了考虑横观各向同性的影响，将GSI变成与岩体材料与结构面控制相关的参数，由此建立的各向异性修正指标可表示为：

GSI=GSI0(SR)+GSI*

(5)

GSI*=D(SR)×(0.3Jv+0.3Jc+0.2Jf+0.2Js)×γ

(6)

式中:

GSI0——GSI初值，由SR确定；

GSI*——GSI增量，由多个维度确定；

SR——岩体结构性等级，D(SR)—SR的值域；

Jv——岩石体积节理比;

Jc——节理断续度;

Jf——岩体摩擦比系数;

Js——节理平直度;

γ—节理弱化乘子。

关于岩体结构性等级SR，Sonmez、Ulusay[12]已给出具体方法，本文不再叙述，利用SR确定初值GSI0和SR的值域，一般而言，对于完整性较好的横向各向同性岩体，GSI0取85，D(SR)取15(见表1)。

表1 岩体结构性参数SR与GSI0取值

2.3 横观各向同性参数的确定

图1给出了概化横观各向同性岩体示意，下面给出5个指标的确定方法。

图1 概化横观各向同性岩体示意

1) 岩石体积节理比Jv

由式(7)确定，能较准确地反映出岩体结构的密度特征，通常来说，节理密度越大，岩石被切割越充分，岩体力学性质越弱。

(7)

式中:

di——垂直方向上相邻节理的距离；

d——为相邻节理的垂向距离的平均值。

2) 节理断续度Jc

由式(8)确定，该指标主要用以概括节理的贯通情况，贯通度越大，岩体强度削弱程度越高。

(8)

式中:

Si——为同一方向相邻节理间断续的距离；

S——该方向上测窗的长度。

3) 岩体摩擦比系数Jf

Jf描述岩体的摩擦性，由式(9)确定，该项系数隐含摩擦角，反映横观各向同性岩体的摩擦强度。

(9)

式中:

φ——岩体的摩擦角，可以通过直剪试验或三轴试验直接获得，分母的含义是经过统计岩石常见岩石摩擦角的取值范围，一般沉积岩取15～50，岩浆岩取45～60，变质岩取25～65。

4) 节理平直度Js

Js描述岩体的摩擦性，由式(10)确定，岩体内节理的平直度对其强度影响十分明显。一般而言，节理起伏越大，互锁能力越好，岩体强度越大(见图2)。

图2 节理平直度(起伏度)示意

(10)

式中:

a——节理波形波谷离测窗底部距离;

d——节理波形波峰离测窗底部距离。

5) 节理弱化乘子γ

由于岩体强度存在各向异性，即随着节理方向的改变，其强度也会发生改变，成典型的“v”型分布。但不同种类的岩石强度随节理倾角变化不一，且缺乏统计该方面的文献，故本文采用节理弱化乘子γ来表征各向异性对岩体强度的弱化，节理弱化乘子γ由式(11)确定：

(11)

式中:

σci——该节理倾角下岩体的单轴抗压强度;

σc——完整岩石的单轴抗压强度，两者可通过试验获取，当缺乏完整岩石的试验数据时，也可取同一批次节理倾角下强度最高试样的抗压强度，一般倾角为90°。

为了岩体横观各向同性性质问题，本文引了5个参数，但在参数的测量上本来就存在一定的误差。对于岩体摩擦比系数Jf和节理弱化乘子γ，其取值与岩石的力学性质有关，可以通过简单的岩石力学试验测得，所造成的误差是可控的。而容易造成误差的主要是岩石体积节理比Jv，节理断续度Jc，节理平直度Js，这3项与岩石几何相关的参数。

根据表1给出的岩石结构性分类，结合式(7)(8)(10)求取参数所需要测得的指标，可见，随着节理切割程度的增加，该几项几何参数测量难度越大，可能造成的认为误差也随之增大，因此，不建议将本文提出的修正准则用于节理形态较为复杂的计算模型中。

对于表1中第1类和第2类岩石，即当SR指标为70～100时，与岩石几何相关的指标：相邻节理的距离，同一方向相邻节理间断续的距离和节理平直度，都能较为精确地进行测量统计，因此，本文建议将本文提出的计算模型用于岩石结构性指标为70～100含节理岩石的力学问题中。

3 数值模拟离散解验证

3.1 数值模型的建立

由于现实中，横观各向同性岩体采样与试验的难度和成本较高，本文采用离散元数值计算的方法对修正的Hoek-Brown强度破坏准则进行验证。

建立横观各向异性岩体模型，尺寸与标准圆柱体式样一致，直径S=50 mm，高d=100 mm。设置水平节理，且节理分布均匀，合理概化，垂向相邻节理距离d1=16.67 mm。横向相邻节理距离为S1，以节理断续度为变量，建立Jc=0.6，0.5，0.4，0.3，0.2，0(贯通)的数值模型见图3。

Jc=0

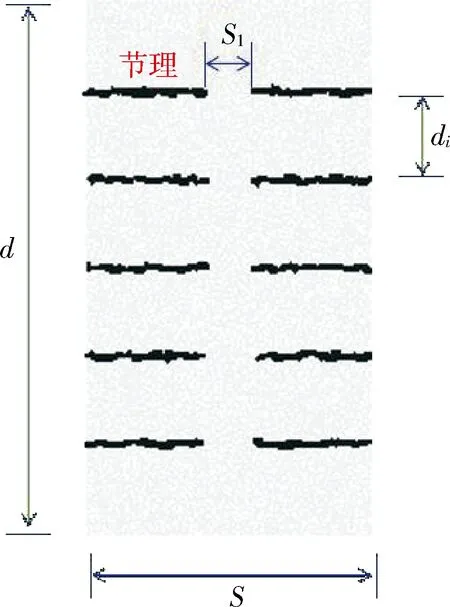
图3 数值模型示意

3.2 模型参数标定

确立了数值试样的几何属性，之后对数值模型的力学属性进行赋值。本文以粤北地区丹霞组(K2E2d的砂岩为对象对数值模型细观参数进行标定。选用平行粘结模型对岩石基质(不含节理，完整试样)进行模拟，采用“试错法”对模型的宏观性质进行标定，建立宏观力学试验模型，在模型中填充颗粒，然后不断调整细观参数，直至细观参数与模型宏观力学参数相逼近为止，细观参数赋值结果见表2、表3所示。

表2 数值模型岩石基质细观参数

表3 数值模型节理细观参数

模型细观参数取值依据如下，采用“试错法”对表2、表3中的模型细观参数进行标定，建立宏观力学试验模型，在模型中填充颗粒，然后不断调整细观参数，直至细观参数与模型宏观力学参数相逼近为止。其中，对于表2中数值模型岩石基质细观参数，采用单、双轴压缩宏观力学试验模型测试2种的岩石材料的泊松比、弹性模量、粘聚力和内摩擦角；对于表3数值模型节理细观参数，采用直接剪切试验模型测试层面的粘聚力和内摩擦角。

图4给出了室内试验和数值模拟单轴压缩下应力应变曲线和试样破坏情况的对比，可见，两者吻合程度较高，说明采用该模型对岩体横观各向同性强度准则的研究时符合实际的。

图4 室内试验与数值计算结果对比示意

施加节理，使其与图3相符合，并对节理参数进行赋值。选用光滑节理接触模型表征节理单元的细观本构关系，再对其力学参数进行赋值(见表3)。用该套细观参数标定结构面的宏观参数，摩擦角φs=32°，粘聚力cs=0.01 MPa，与实际相符。

3.3 数值离散解对修正Hoek-Brown强度破坏准则的验证

3.3.1数值离散解

对建立好的数值模型展开双轴试验，σ3分别设置为5 MPa，10 MPa，15 MPa，20 MPa，加载至试样破坏，记录其峰值强度。峰值强度随节理断续度的变化呈现规律如图5所示。

图5 不同节理连续度下横观各向同性岩体单双轴峰值强度对比示意

由图5可见，不同节理连续度下横观各向同性岩体的峰值强度呈现出如下规律：① 峰值强度随围压增大而增大，表现为压硬性，同时其趋势为非线性增长；② 随着节理断续都的减小，横观各向同性岩体的强度随之降低，即节理贯通度越大，岩体的峰值强度越小。

3.3.2修正的Hoek-Brown强度准则

需要确定的参数为：① 不同节理连续度下横观各向同性岩体的单轴抗压强度σc，上文通过数值试验已得到(如图5所示)，当σ3为0时对应的即为各模型的峰值强度；② Hoek-Brown常数m、s、a，可通过扰动系数D和岩体地质强度指标GSI计算得到。

对于扰动系数D，根据工程岩体分级标准(GB/T 50218—2014)确定，结合采样地区实际工况确定：由于本文采样地区地质情况较好，人为扰动较少，且数值计算是基于概化模型的计算，因此，本文研究中将扰动系数D设置为0；而式(2)的mi，结合试样类别和晶粒尺寸，通过查表确定为14.5。

对于GSI，采用式(5)(6)进行计算。需要确定的参数由GSI0，D(SR)，Jv，Jc，Jf，Js和γ，确立过程讨论如下：① 由表1可知，本文建立的数值模型属于第1类结构，故GSI0=85，D(SR)=15；②Jc为本文数值模型的变量，可通过赋予节理不同的几何参数确定，其取值范围在0～0.6间;③ 根据图3模型建立的几何属性，根据式(8)(10)，确定岩石体积节理比Jv=0.58，节理平直度Js=0.5；④ 参数Jf和γ与试样力学属性相关，相关力学参数由数值模拟结果得到，并通过式(9)(11)得到。其中，求取γ的指标σci，σc对应于图5当σ3为0时个模型的峰值强度；进一步地，可以通过图5不同σ3下各个试样的峰值强度，绘制σ1～σ3最佳关系曲线(直线)，求得相应的摩擦角。

最终，将上述参数代入式(5)(6)中，得到横观各向同性岩体GSI参数(见表4所示)。

根据表4得到的参数，根据式(2)(3)和式(4)计算得到修正的Hoek-Brown参数m、s、a(见表5所示)，代到式(1)中，可得到横观各向同性修正的Hoek-Brown模型。

表4 横观各向同性数值模型GSI参数

表5 修正的Hoek-Brown参数

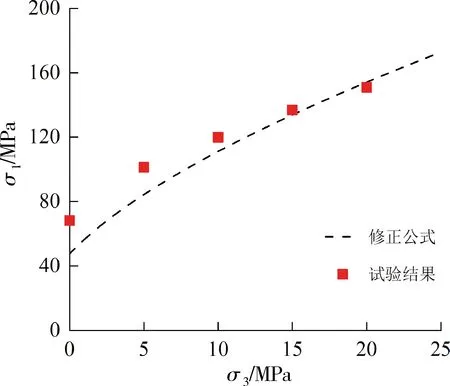
将修正的Hoek-Brown模型和数值计算得到的离散解投影到同一坐标轴上(如图6所示)，由图6可见，修正的Hoek-Brown强度曲线具有良好的拟合效果，说明本文的修正的强度准则能很好地表征岩体的横观各向同性；围压越高，修正曲线的拟合效果越好，说明修正公式能采用较少的低围压的参数对高围压下峰值强度进行准确预测，在实际工程尤其是高应力场下的横观各向同性岩体工程中具有良好的指导意义。

4 结语

1) 本文通过引入岩石体积节理比Jv，节理断续度Jc，岩体摩擦比系数Jf，节理平直度Js和节理弱化乘子γ5项指标，对Hoek-Brown强度破坏准则进行了修正，使其能为清晰地表征岩体的横观各向同性；

2) 通过离散元数值计算的方法对修正的强度破坏准则进行了验证，结果表明，修正的Hoek-Brown曲线能很好地拟合数值计算下的离散解，说明本文提出的修正理论有着良好的预测效果；

3) 围压越高，修正曲线的拟合效果越好，说明修正公式能采用较少的低围压的参数对高围压下峰值强度进行准确预测，使“不可测得”的区域变得更加清晰，可为实际工程设计提供实质性的预测和指导。