某斜拉桥风致抖振作用及减振控制设计

彭 喆，任司南

(1.中铁第四勘察设计院集团有限公司，湖北 武汉 430000；2.株洲时代新材料科技股份有限公司，湖南 株洲 412007)

1 概述

风无时无刻不存在于自然界中，与我们的生活也息息相关。风给人类的生产生活带来了一定影响[1]。桥梁结构在风的振动作用下将产生振动响应[2]。风对桥梁的作用是较复杂的空气动力现象[3-4]。本文以某特大跨度斜拉桥为工程背景，研究了该桥在最大悬臂施工状态及成桥状态的风致抖振作用及减振控制设计，并与风洞试验结果进行了对比分析，进而判定桥梁在紊流场中的安全性。

2 抖振力及振动方程

抖振力公式最早由Davenport[5]研究并提出，他利用概率统计的方法、基于片条理论假设的随机振动理论以及准定常空气动力理论假设，求解了柔性细长结构的风振响应。Scanlan 等学者对Davenport理论进行了修正，在抖振力中考虑了阻力系数及导数的影响。紊流中桥梁加劲梁单位长度的抖振力为[6-8]：

(1)

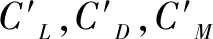
其中，α为风攻角；χLu，χLw，χDu，χDw，χMu，χMw均为气动导纳；u，w分别为纵向和竖向脉动风速分量。

用u(x,t)表示竖向振动位移,主梁振动的一般微分方程为:

(2)

其中,m为主梁单位质量；c为主梁单位长度的阻尼；k为主梁单位刚度；L(x,t)为单位脉动风荷载。

假定竖向振型的频率ω1已知,振型函数为η(x),振型阻尼比为ζ1,则振型坐标变换有:

u(x,t)=h(t)η(x)

(3)

其中,h(t)为主梁一阶竖向振型广义坐标。

将式(3)代入式(2),方程两边乘上η(x),再对x积分,有:

(4)

斜拉桥主梁每单位跨度升力为:

L=Lse+Lb

(5)

其中自激力Lse可表示为:

(6)

其中结构Lb所受的抖振力可表示为:

(7)

将式(5)～式(7)代入式(4),并将自激力项移到等式左端,合并得:

(8)

3 脉动风速功率谱及风速模拟

根据抗风规范[9],合成脉动风速的模拟数据，仅列出两组最大悬臂施工阶段水平及竖向脉动风数据,如图1,图2所示。

4 工程背景

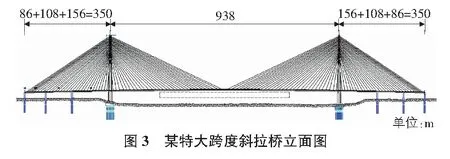
某特大跨度斜拉桥为双塔双索面钢箱梁斜拉桥,跨度为86 m+108 m+156 m+938 m+156 m+108 m+86 m。桥梁主梁采用流线型扁平钢箱梁,风振控制跨度为938 m,主梁离地面高度为30.5 m,地面粗糙高度为0.01 m,主梁处平均风速29.6 m/s。该桥立面图见图3。

不同攻角下主梁断面三分力系数及三分力系数斜率如表1所示。

表1 不同攻角下主梁断面气动力参数

5 桥梁风振响应及减振控制设计

5.1 桥梁最大悬臂状态风振响应

大跨度桥梁在施工阶段风致振动响应更大。斜拉桥的最大双悬臂状态和最大单臂状态就是这种最不利的状态。根据风洞试验结果,当风致振动为抖振作用时,桥梁最大单悬臂施工状态下,主梁均发生了不同程度的抖振现象,抖振位移随着风速的增高而逐渐增大,且最大风速下主梁的抖振响应较大。下边列出风洞试验及数值计算结果,其中包络值是指不同阶段三组脉动风在不同攻角下最大风致振动响应值。表2为最大风速下桥梁最大悬臂施工状态位移响应包络值。

表2 最大风速下桥梁最大悬臂施工状态位移响应包络值

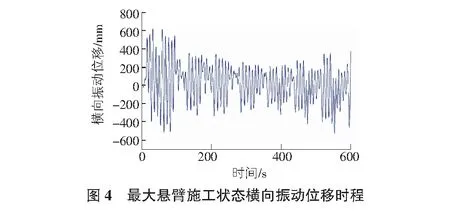
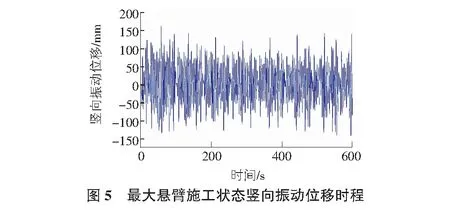
从表2可以看出,桥梁在最大悬臂施工状态下,数值计算结果与风洞试验结果均表明,最大风速下主梁的抖振响应较大,横向振动位移响应达到606.6 mm,竖向振动位移响应达到170.6 mm,横竖向位移响应都较大,严重影响施工阶段桥梁的安全性及施工人员的安全。图4，图5为桥梁最大悬臂施工状态下主梁横向振动位移时程和竖向振动位移时程,表明桥梁在最大悬臂施工状态下振动位移幅值较大。

5.2 桥梁成桥状态风振响应

由于桥梁的跨度较大,桥址处主梁最大风速达到了34.9 m/s,所以桥梁成桥状态风振响应也成为桥梁的主导荷载。根据风洞试验结果,成桥状态下,当风为紊流风时,主梁发生了不同程度的抖振现象,最大风速下主梁的抖振响应最大。下边列出风洞试验及数值计算结果,其中包络值是指不同阶段三组脉动风在不同攻角下最大风致振动响应值。表3为最大风速下成桥跨中位移响应包络值。

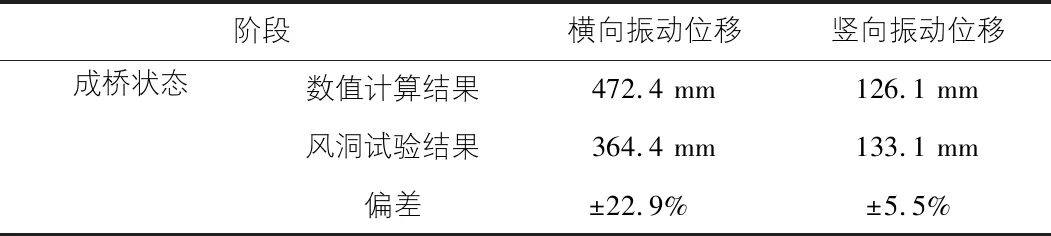
表3 最大风速下成桥跨中位移响应包络值

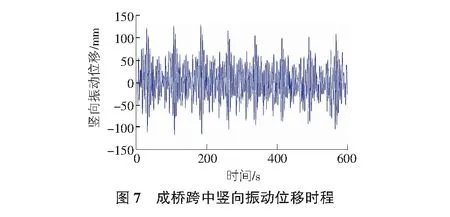
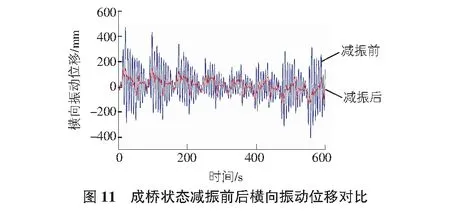
由表3可以看出,桥梁在成桥状态下,最大风速下主梁的抖振响应较最大悬臂施工状态时小,这是由于成桥状态桥梁刚度较大,稳定性好,变形相对小。成桥状态下,桥梁跨中横向振动位移响应达到472.4 mm,竖向振动位移响应达到133.1 mm,横竖向位移响应也比较大,同样会影响施工阶段桥梁的安全及施工人员的安全。图6，图7为桥梁成桥跨中处横向振动位移时程和竖向振动位移时程,也表明桥梁在成桥状态下跨中振动位移响应也比较大。另外,由表3可知,成桥状态下桥梁跨中横向振动位移数值计算结果较风洞试验结果偏大,这是由于数值计算过程中考虑桥梁横向抗风支座的实际有限弹性刚度所致。

5.3 桥梁风振减振控制设计

调谐质量阻尼器(TMD)系统是一种抑制主结构振动的有效装置,当其参数调整合理时,桥梁振动控制比较有效。根据桥梁实际受力情况,提出了多重调谐质量阻尼器(MTMD)方法[10-11]。多重调谐质量阻尼器的风振控制的力学模型如图8所示,其中m1,m2,…,mN为N个TMD的质量；k1，k2，…，kN为N个TMD的刚度；c1，c2，…，cN为N个TMD的阻尼；ms，cs，ks分别代表桥梁的质量、阻尼和刚度。

在抖振作用下,桥面的位移为ys(x,t);第i个TMD的位移为yi(x,t)；风荷载为f(t);则主梁的动力平衡方程为:

(9)

第i个调谐质量阻尼器的动力平衡方程为:

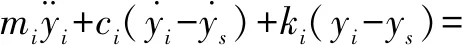
(10)

将桥梁与多重调谐质量阻尼器的动力平衡方程相加:

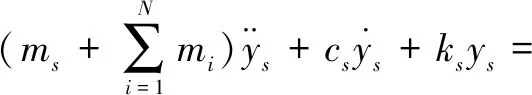
(11)

根据MTMD放置的最优原则以及对MTMD的参数优化结果,桥梁最大悬臂施工阶段横桥向需要设置4个7.5 t的TMD,单个TMD的尺寸为3 m×2 m×1 m;竖向需设置1个7.5 t的TMD,单个TMD的尺寸为1.8 m×2.1 m×1.5 m;桥梁成桥阶段横桥向需要设置4个7.5 t的TMD,单个TMD的尺寸为3 m×2 m×1 m;竖向需设置3个7.5 t的TMD,单个TMD的尺寸为1.8 m×2.1 m×1.5 m。对桥梁风振减振控制设计后,桥梁的位移响应包络值如表4,表5所示。

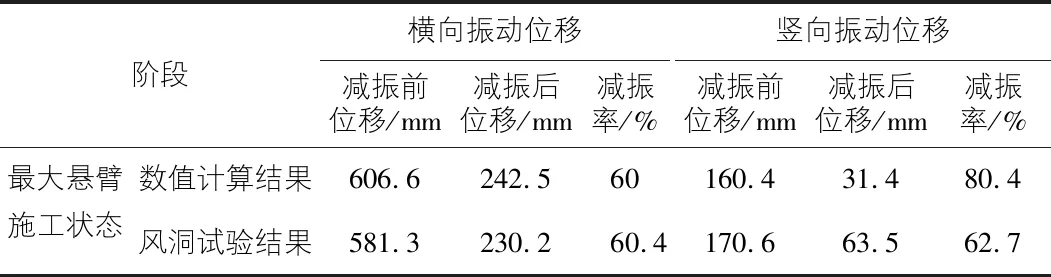
表4 最大风速下桥梁最大悬臂施工状态位移响应包络值

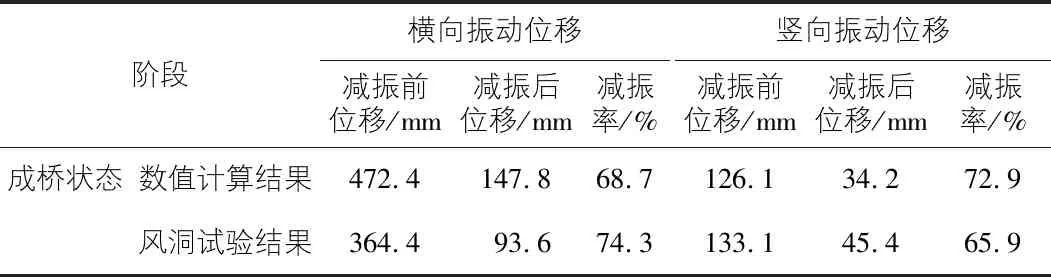
表5 最大风速下成桥跨中位移响应包络值

从图9～图12可以看出,最大悬臂施工状态和成桥状态减振设计前后,MTMD减振效果明显。由表4，表5可以看出,数值计算和风洞试验结果,桥梁最大悬臂施工状态横向振动位移减振率分别为60%和60.4%,竖向振动位移减振率分别为80.4%和62.7%;成桥状态横向振动位移减振率分别为68.7%和74.3%,竖向振动位移减振率分别为72.9%和65.9%。

5.4 桥梁舒适度评判

当结构抖振响应较大时,会影响成桥状态的安全性。根据狄克曼指标K[12],可以进行结构舒适度的评判。

水平向判定过程:当f<2 Hz时,K=2Df2;当2 Hz≤f≤25 Hz时,K=4Df;当f>25 Hz时,K=100D。

竖向判定过程:当f<15 Hz时,K=2Df2;当15 Hz≤f≤40 Hz时,K=4Df;当f>40 Hz时,K=100D。其中,D为桥梁结构振动幅值,mm;f为桥梁结构振动频率,Hz。

根据狄克曼指标对桥梁风振减振控制设计前后进行判定和比较,结果如表6所示,由表6可知,桥梁减振控制后,横向振动和竖向振动狄克曼指标K均在10以下,介于能忍受任意长时间振动和能忍受短期振动之间,可基本满足施工及桥梁安全要求。

表6 桥梁风振控制前后狄克曼指标比较

6 结论

1)数值计算结果与风洞试验结果表明,桥梁在最大悬臂施工及成桥状态下,主梁均发生了不同程度的抖振现象,且最大风速下主梁的抖振响应较大。桥梁最大悬臂施工状态横向位移达到606.6 mm,竖向位移达到170.6 mm;成桥状态横向位移达到472.4 mm,竖向位移达到133.1 mm。

2)对桥梁进行了风振减振控制设计,根据MTMD放置的最优原则以及对MTMD的参数优化结果,桥梁最大悬臂施工阶段横桥向需要设置4个75 kN的TMD,竖向需设置1个75 kN的TMD;成桥阶段横桥向需要设置4个75 kN的TMD,竖向需设置3个75 kN的TMD。悬臂施工状态风振减振率最大达到80.4%,成桥状态风振减振率最大达到74.3%。

3)对桥梁减振控制设计后的舒适度进行了判定,桥梁横向振动和竖向振动狄克曼指标K均在10以下,介于能忍受任意长时间振动和能忍受短期振动之间,可基本满足施工及桥梁安全要求。