滑带土蠕变本构模型综述

郭 威

(河南省地质矿产勘查开发局第二地质矿产调查院,河南 郑州 450001)

滑坡形成原因复杂、影响因素众多且破坏性强。据环境监测院发布2019年全国地质灾害通报:2019年,全国共发生地质灾害6 181起,直接经济损失达27.7亿元。其中,发生滑坡4 220起,占地质灾害总数的68.27%,相比2018年大幅增加[1]。20世纪以来,滑坡地质灾害的频发严重威胁着人民的生命财产安全,这也使得越来越多的科研人员开始研究滑坡的形成机制和影响因素。滑坡的发生是多方面作用的结果[2-3],影响因素总体可分为内部因素和外部因素,内部因素包括岩土体的性质,结构构造和初始应力状态;外部因素主要包括水的作用,岩体风化以及人为干扰[4]。

孙淼军等[5]通过分析三轴试验的结果,发现滑带土与滑坡的变形阶段具有一致性,提出滑带土的物理力学性质影响、控制着滑坡整体的演化发展。刘清秉等认为大多数坡体的滑动呈缓慢的阶梯式运动,表现出明显的蠕变特性。然而,国内外对于滑带土的研究较多的集中于通过现场试验、室内试验和理论分析等研究滑带土的蠕变特性,而以此为基础建立合理本构模型的研究相对较少。岩土体本构模型是能够反映岩土材料应力应变关系的数学模型,适用于滑带土的蠕变特性研究的本构模型大致可以分为四类:经验模型、元件模型、内蕴时模型、屈服面模型。本文将就这四类本构模型的发展情况进行归纳总结,以期发现未来的研究方向。

1 经验模型

经验模型即通过对土体进行试验,抽象处理试验结果获得相应的应力-应变关系。一般的经验模型难以描述非线性加速蠕变阶段。土体蠕变的过程是一个应力-应变-时间关系变化的过程,可以归纳为式(1)函数,其中应力应变函数f1一般用指数函数、双曲线函数等来描述,而应变-时间函数f2用幂函数来描述,本文就应用较为广泛的经验模型Singh-Mitchell模型和Mesri模型进行介绍。

ε=f1(k)f2(t)

(1)

1.1 Singh-Mitchell模型

Singh-Mitchell[6]于1968年总结了单级加载下蠕变三轴试验相关结论,提出了三参数本构模型,该模型通过指数函数来描述应力-应变关系,通过幂函数描述应变-时间关系。

(2)

化简式(1)得到:

(3)

式(2)即为Singh-Mitchell模型,它能较好的描述剪应力水平在20%～80%以内土体的应力-应变-时间关系,且不受排水条件,是否扰动影响,参数β的稳定性保证了该模型的稳定性和适用性。王常明等[7]在研究滨海相沉积的软土的蠕变特性时指出,Singh-Mitchell模型应力-应变关系用双曲线来描述是合适的。卢萍珍等[8]用Singh-Mitchell模型和Mesri模型模拟湖南竹城公路路基软土蠕变效果不佳,提出用幂函数描述应力-应变关系,用双曲线函数描述应变-时间关系能较好的反映该地软土的蠕变特性。刘业科等[9]同样在研究湖南竹城公路软土的蠕变特性时,使用Singh-Mitchell模型计算结果与实验结果有较大的误差,用双曲线函数替代幂函数描述应变-时间关系提出了修正的Singh-Mitchell模型。

1.2 Mesri模型

康纳(Kondner)于1963年通过整理分析大量三轴试验数据建立了能够模拟土体应力应变特性的双曲线方程:

(4)

则其切线模量为:

(5)

当ε1=0,初始切线模量:

(6)

当ε1→0时,有：

(7)

实际试验中一般取一定值来确定土的强度(σ1-σ3)f,定义破坏比:

(8)

将式(6)～式(8)代入式(5)得到:

(9)

Mesri模型以上述双曲线模型描述应力-应变关系,用和Singh-Mitchell模型同样的幂函数来描述应变-时间关系,则将式(6)代入式(3)得到Mesri蠕变方程:

(10)

Mesri模型相较于Singh-Mitchell模型不再受应力状态限制,适用于任何剪应力状态下的土体蠕变特性描述。王琛等[10]提出大多数研究认为与时间相关的参数λ为常数,使得Mesri模型在衰减蠕变、等速蠕变和稳定阶段描述蠕变特性效果欠佳。提出在不同的蠕变阶段取不同范围λ值,并给出了参考取值范围,建立了改进的Mesri模型。赖小玲等[11]开展了一系列非饱和三轴蠕变试验,通过建立吸力与初始切线模量的函数,在Mesri模型的基础上建立了能反映土体应力-吸力-应变-时间关系的模型,该模型能较好的描述各级含水率下滑坡滑带土的蠕变特性。黄海峰等[12]指出Mesri模型用幂函数描述应变-时间关系难以准确描述稳定蠕变阶段,他们提出用Log-Modified函数取代幂函数建立了新的经验模型,并通过试验验证了该模型的正确性。王元战等[13]通过试验指出软黏土的变形可以归结为两个部分,第一部分呈线性变形,第二部分为蠕变变形。在Mesri模型的基础上,通过引入维亚洛夫时间函数实现了用双曲线函数描述应变-时间关系,建立了新的经验模型。

从发表的文献可见,经验模型具有特征性,针对不同性质、不同应力路径等条件的土体应采用不同的模型。多数对于模型的优化也不是一概而论的使其具有普适性,而是针对不同的土体建立尽可能契合的模型。因其灵活、方便,但相对缺乏理论支持,所以较少地应用于工程项目。

2 元件模型

蠕变不仅受到应力应变状态的影响,还需要考虑时间因素。传统的纯应力应变行为分析做不到这一点,于是人们开始考虑把岩土体的黏弹塑特性分开考虑再进行整合,用合适的黏性模型来拟合岩土的蠕变,最后基于数据资料对理想弹性模型、理想塑性模型以及与理想黏性模型进行组合来建立符合岩土体黏弹塑性的本构模型。该类模型灵活度高、切合实际,且其图形表达也十分方便,用代表性元件进行串联、并联组合即可。

一般用胡克模型作为理想弹性模型,用弹簧作为元件,用来描述滑带土蠕变的弹性特性部分,其表达式如下:

σm=Kεv

(11)

(12)

其中,E为弹性模量；v为泊松比；K为体积弹性模量。

理想塑性模型一般被认为是刚塑性模型,用摩擦元件描述岩土体的塑性特性部分,其表达式:

(13)

其中，λ为比例常数;Hij为起始摩擦力,作为开始发生塑性变形的条件。

一般用牛顿黏滞模型作为理想黏性模型,用阻尼元件来描述,阻尼元件是一个盛满牛顿液体和一个活塞的黏壶,通过活塞的移动来模拟黏性应变速率,用牛顿液体对活塞造成的阻力来模拟应力。其表达式如下:

(14)

以上是三种最简单的元件,通过这些元件的组合来建立黏弹塑性模型得到了国内外学者的广泛认可和应用,下面举例进行介绍。

2.1 西元模型

西元模型,又称宾厄姆-沃格特模型(B-K模型),该模型是由宾厄姆模型和开尔文模型串联组成[14]。它是由三个部分组成,一个理想弹性模型,一个由理想黏性模型和理想塑性模型组成的黏塑性模型以及一个理想弹性模型和一个理想黏性模型组成的黏弹性模型,其模型图如图1所示。

西元模型的蠕变可由式(15)表示:

(15)

西元模型能够较好的模拟岩土的流变特性,而且模型简单、适用性广,所以应用十分广泛。但是随着进一步研究,人们认识到岩土蠕变可分为三个阶段:衰减蠕变阶段、稳定蠕变阶段和加速蠕变阶段,西元模型无法描述加速蠕变阶段。许多学者开始研究改进西元模型以追求更好的描述岩土变形特性。曹树刚等[15]提出黏滞系数在岩石受压至破坏的短时间内先增大后减小,建立了新的黏滞模型取代原西元模型中的黏滞模型来体现这一特性,使得广义西元模型能描述非线性加速蠕变阶段。马白虎[16]通过引入蠕变加速阶段非线性函数来改进西元模型。田小朋等[17]通过添加一个含水元件来提高模型准确性。范翔宇等[18]通过基于实际情况改变衰减指数来优化西元模型。蒋海飞等[19]考虑高围压下孔隙水压力的影响对Kelvin体进行修正优化了西元模型。陈航等[20]通过温度膨胀系数建立了可以考虑温度影响的西元模型。

2.2 河海模型

河海大学徐卫亚等[21]建立了一个可以描述岩土体加速流变过程的黏弹塑性模型,并命名“河海模型”。该模型在线性黏弹性流变模型的基础上串联一个非线性黏塑性模型,使模型能综合考虑岩土流变过程中的弹性特征、塑性特征、黏弹性特征和黏塑性特征。河海模型是一个将二者串联起来的元件模型，其元件图如图2所示。

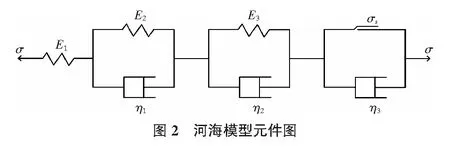
河海模型蠕变方程:

(16)

当假设流变指数为1时,该模型退化为西元模型,可见河海模型较西元模型更具有普遍意义。

2.3 Burgers模型

Burgers模型由麦克斯韦尔模型和开尔文模型串联而成,该模型能较好地描述加速蠕变阶段之前的蠕变特性。

袁海平等[22]建立了M-C塑性元件,将其与Burgers模型串联建立了能够描述黏弹塑性偏量特性和弹塑性体积行为的改进Burgers模型。秦玉春提出开尔文模型剪切模量GK具有时间相关性,进行了非定常参数拟合。朱明礼等[23]通过引入非确定时间参数建立变参数模型本构关系,得到时间相关非定常Burgers模型。熊良宵等[24]用非线性黏滞体替换Burgers模型的麦克斯韦尔体,建立了一种非常定Burgers模型。康永刚、张秀娥[25]提出直接将非定常参数代入Burgers模型有局限性,实际应用困难。他们通过构造非常定黏壶建立新的非常定Burgers模型。朱端等[26]用Able黏壶替代牛顿黏壶建立了分数阶Burgers模型。

元件模型因其直观、方便、易懂的优点,使得其在实际工程得到了广泛的应用,对于元件模型的研究也越来越多。熊良宵等[27]指出通过元件的组合不能解决元件模型无法描述加速蠕变阶段的问题,认为元件模型在我国的发展趋势是构建非线性蠕变本构模型以求模拟岩土体蠕变发育的整个过程,他们归纳整理了元件模型非线性化的六个途径:

1)引入非线性牛顿体。2)引用基于摩尔-库仑准则建立的M-C塑性元件。3)将黏弹性模量或者黏滞系数用与时间相关的非常定函数表达,建立非常定蠕变模型。4)引入损伤力学理论、断裂力学理论等。5)添加功能性元件。6)引用非线性黏壶元件替换牛顿黏壶。元件模型的缺点是它是一种基于表观现象建立的模型,没有从岩土体流变机制的本质出发进行研究。这也就导致在一定引力路径下适用的模型可能在另一应力路径下不再适用,各种复杂应力加载条件下使用元件模型也会比较困难。

3 内蕴时理论模型

Valanis.K C[28]最早于1971年提出了内蕴时间理论,后经过不断地完善和发展被逐渐应用到各种材料本构关系的描述。其基本理论是:基于热力学理论,认为在塑性与黏塑性材料中,任一点的应力状态是其邻域内材料变形与温度历史的泛函,定义一个反映材料内部性质,随材料内部变化和外部时间变化的内蕴时间。用内变量来描述材料的不可逆变化,得到内变量的变化规律建立本构模型。内蕴时模型本构方程具有遗传积分的形式,以内蕴时间作为积分变量区别于传统黏弹塑性本构方程以牛顿时间作为积分变量[29]。

内蕴时模型的优势在于它跳脱了传统黏弹塑性模型的束缚,不以屈服面作为理论基点。传统本构理论大多是以金属材料为研究对象建立的,而岩土材料应力应变关系较之于金属材料明显更为复杂,学者们把相关本构模型应用到岩土体研究尤其是较为复杂的蠕变研究过程中,由于模型预测数据与实际情况相去甚远而采取一些没有实际意义的混乱做法,走了很多弯路。相较于传统本构理论基于许多假设却又想包罗万象,以热力学基本思想作为理论基础的内蕴时模型明显更具有普适性[30]。然而,有些学者提到:具有广泛适用性的代价就是内蕴时模型无法给出一个固定、切实可行的计算规程。一方面,普适性使得建立某种材料的内蕴时模型需要确定的待定参数非常多;另一方面,内蕴时的合理定义是内蕴时模型能较好描述岩土体本构关系的关键,然而内蕴时理论没有提出定义内蕴时的具体做法。

内蕴时模型的研究热潮在二十世纪七八十年代,二十一世纪初还有较多研究,而从现在发表文献的数量和内容来看,内蕴时岩土本构模型的研究已经逐渐放缓,其原因可能是:一方面,由上述提到的问题导致实际应用比较困难;另一方面,当前对岩土体的研究追求从微观机理出发,研究岩土体在应力作用变形破坏的本质。于是,无论是实际应用还是科学研究内蕴时模型的空间越来越小。但是,笔者认为滑带土蠕变强调应力-应变-时间的关系,软岩的流变就是一个不可逆热力学的过程[31]。这些特点与内蕴时模型的理论依据是十分契合的,应用内蕴时模型描述滑坡的蠕变特性或许是一个不错的选择。

4 损伤断裂模型

在荷载的作用下,岩土体内部会逐渐积累微小裂隙,最终造成局部剪切带的产生。这是一个明显的结构性特征,一部分学者曾尝试用断裂力学的理论来解释岩土体的强度变形特征,但由于参数计算过于困难等原因导致该类模型没有得到广泛认可。又有学者提出用损伤力学、细观力学从微观到宏观来反映土体的结构性具有可行性,岩土体损伤力学模型得以发展。

4.1 断裂力学与损伤力学理论

20世纪20年代,Griffith最先提出了材料裂纹长度会影响材料强度,其理论是断裂力学理论的开端。1948年,Irwin将Griffith理论发展完善成一套体系,并应用于工程实际,使得断裂力学开始发展。1968年,J.Rice定力奇异场的概念,为断裂力学奠定理论框架。60年代,断裂力学被逐渐引用到地学,岩土断裂力学也逐渐兴起。断裂力学是研究材料内部裂纹的破坏规律,及其对材料强度造成影响的一门学科,将断裂力学理论应用到对岩石材料的强度分析当中就是岩石断裂力学。

岩土体的损伤指在不同加载条件下,岩土体力学性能不断衰减的过程。损伤力学研究的是加载条件下,损伤随着变形直至破坏的发展规律。同时用损伤变量这一概念来描述材料从损伤到断裂、破坏的过程,记作D,当D=0时,材料处于无损伤的状态;当D=1时,材料完全破坏,可见D的取值处于0～1之间。损伤变量D的确定方法有许多种,主流的方法有两种。其一是通过试验获得岩土体性能参数来确定的宏观损伤力学方法;其二是结合统计学的方法统计微裂隙的数量、面积等来确定损伤变量D的细观损伤力学方法。确定损伤变量的方法不同,形成了不同的岩土体损伤本构模型。

以沈珠江损伤模型为例简单介绍连续介质损伤力学。1993年,沈珠江通过研究结构性土的应力应变关系,发现了许多传统弹塑性模型无法解决的问题,他提出将损伤力学引入到对结构性土的研究中,建立了沈珠江损伤力学模型[32],属于宏观损伤力学模型的一种。该模型把岩土体分为原状土和完全破坏土,通过二者的权重的变化来体现岩土的损伤程度,可以用下式表达:

S=(1-w)Si+wSd

(17)

其中，Si为原状土的力学特性;Sd为损伤土的力学特性;w为损伤比。

然后通过假设原状土、损伤土的屈服变形以及屈服比带来的变形三个部分共同构成土体的塑性形变的应力应变关系。1999年,兑关锁[33]、沈珠江提出直接通过对总应变求增量来获取应力应变增量关系,计算该关系式只需损伤土回弹模量和损伤比,得以简化。

统计损伤模型是说岩石因其不均匀性、不连续性、各项异性使其应力应变关系复杂,岩土体内部的微裂隙、结构面、孔洞等的分布具有随机性,在压力作用下岩土体内部产生损伤的分布也具有随机性。单纯通过拟合实验数据曲线来建立本构模型无法考虑这一点。Dusan Krajcinovic[34-35]于1982年提出基于强度概率理论和损伤力学理论建立损伤本构模型,本构关系可以用下式表示:

(18)

该理论把岩土体试样抽象成若干杆集合。其中,n为断裂杆；N为杆总数,服从Weilbull分布。该理论为损伤力学的研究开辟了一条新的思路。1992年,唐春安[36]认为岩土体内部的缺陷服从泊松分布,微元具有线弹性且强度服从正态分布建立了统计损伤本构模型。1998年,曹文贵等[37]提出岩土体微元强度不仅仅受微裂隙随机分布的影响,还受微元体应力状态的影响。通过引用应变等价假说[38]建立了考虑岩土体围岩压力的统计损伤模型。2002年,徐卫亚等[39]综合考虑裂隙分布与应力状态,在已有理论的基础上提出引用一个受拉参数来优化受拉阶段有效应力的计算,提出了一个能够较好描述岩土应力应变变化全过程的损伤统计模型。其损伤变量表达式如下:

(19)

其中，f(σ*)为有效应力;P为损伤概率的密度分布。它是一种典型的细观损伤力学模型。统计损伤模型能较好地反映岩土体的破坏过程,能体现应变软化这一特征。它还能够体现岩石强度随着围岩压力增大而增大的应力应变关系,具有广阔的发展前景。2012年,张友锋、蔡美峰[40]在第十二次全国岩石力学与工程学术大会上系统总结了已有的统计损伤本构模型,提出了如何更准确地表达参与强度是这类模型的重要发展方向。

损伤力学解释的岩土体从损伤到破坏的细观过程与滑带土的宏观发展有较好的统一性,将损伤理论应用到岩土体本构模型中能较好的模拟滑带土蠕变的各个阶段。金丰年等[41]用割线模量定义损伤变量,建立了非线性流变损伤本构模型;朱昌星等[42]定义时效损伤变量,应用到一个能反映加速蠕变的元件模型当中,建立了岩石非线性蠕变损伤模型;蒋昱州等[43]提出损伤的发生主要是在加速蠕变阶段,且呈现明显的非线性特征,给出了相应损伤演化方程,将该方程应用到Maxwell模型当中建立了改进的Maxwell模型。

4.2 断裂力学与损伤力学耦合

滑带土物理力学性质复杂,其蠕变特性不仅受到时间因素影响,而且与降雨条件联系紧密。经典的断裂力学理论无法解决滑带土的蠕变问题,因为蠕变过程中,岩土体不仅仅产生裂纹,还会产生各种损伤。有学者形象地把它比喻为分布损伤,而把裂纹比喻为奇异损伤,认为岩石内部在产生裂纹之前就已经分布着微裂隙,这些微小裂隙也会对岩土体的强度造成影响。滑带土对应岩土体产生裂纹之前是衰减蠕变阶段和稳定蠕变阶段,对应裂纹产生以后发生加速蠕变。因此,用损伤力学理论描述衰减、稳定蠕变阶段,断裂力学理论模拟加速蠕变阶段是一种思路。

然而,杨圣奇指出,岩土体宏观裂隙的产生没有一个明确的界限,即滑带土蠕变过程中,衰减蠕变阶段、稳定蠕变阶段也有裂纹产生,加速蠕变阶段也伴随着微裂隙的产生,这都会影响土体强度,如何有效地对损伤力学和断裂力学进行耦合是一个待解决的问题。凌建明[44-45]于1995年最早将损伤力学与断裂力学结合,用损伤力学的理论来分析裂纹的起裂和扩展,建立了损伤累计模型;1999年,陈卫忠等[46]以三峡船闸高边坡为例子分析其节理裂隙损伤耦合效应,并建立了黏弹塑性损伤耦合本构模型;2008年,赵延林等[47]提出岩土体内裂隙纵横交错,试图逐一描述每条裂纹的起裂与扩展难以实现。因此,将断裂力学与损伤力学理论结合起来是必要的,建立了裂隙岩体渗流-损伤-断裂耦合模型。

5 结语

滑坡蠕变的过程是缓慢、长期进行的,其变形机制受到滑坡物质的蠕变特性控制,而滑带土的变形特性具有明显的时间效应。因此,在研究滑带土应力应变关系时应当考虑时间因素。经验模型能具有针对性地建立契合工程中遇到的各类岩土体的本构模型,双函数的形式充分考虑了应力-应变-时间的关系。虽然不具有普适性,但胜在简单、便捷。蠕变元件模型可以通过优化、添加元件等手段考虑时间、吸力等各种影响因素,灵活性强。内蕴时理论是一个基于热力学理论建立的框架,通过定义内蕴时用内变量来模拟岩土体的应力状态。内蕴时理论不受屈服面理论束缚,具有普适性。断裂损伤耦合模型能从岩土体内部结构的损伤机理出发,模拟蠕变滑坡各个阶段的应力应变关系,既考虑了岩土体的结构性,又能解释滑坡的宏观变形。

目前,滑带土蠕变特性本构模型的研究在衰减蠕变阶段和稳定蠕变阶段已经取得了许多成就,如何更好地模拟非线性加速蠕变阶段是当下正在攻克的难关。其中,元件模型和损伤力学理论在这方面有一些实践、进展。另外,进入信息时代,以基于神经网络建立的岩土体本构模型为代表的智能岩石力学或许能带来一些突破。