车用燃料电池氢气循环系统引射特性研究
赵海贺, 陈泽宇, 覃承富, 郭晓冰
(东北大学机械工程与自动化学院,辽宁 沈阳 110819)
0 引言
随着环境与能源问题日益严峻,发展替代能源汽车已成为世界各大汽车厂商及科研机构的研究热点[1—4]。燃料电池电动汽车凭借能量转换效率高、零污染且能源来源广泛的技术优势,被普遍认为是未来汽车发展的重要趋势之一[5—9]。当下普遍采用的质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)具有启动快、功率密度高、易密封的特点,可通过供应过量氢气的方法来保证输出功率的稳定。电堆阳极产生的废气中包含水和一定量未反应的氢气,因此,PEMFC非常依赖氢气循环系统来实现对阳极残余废气的循环利用,从而提高电池的燃料利用率和电池效率。引射器是氢气循环系统的重要组成部分,负责回氢系统的引射、混合、压缩等多种功能[10—13],然而引射器的工作性能受流体压力、尺寸结构等多种因素影响,且存在强烈的非线性、流固耦合问题,因此,如何实现引射器的高效运作和优化设计是当前亟需解决的重要技术问题。
目前研究人员对引射器实验与仿真方法进行了广泛研究。文献[14]采用实验与数值模型结合的方式研究了喷嘴面积与流体压力对引射器性能的影响,结果发现通过改变喷嘴面积和流体压力可以实现对引射性能的控制。文献[15]采用3种湍流模型对引射器进行数值模拟,结果发现剪切应力运输(shear stress transport,SST)k-ε湍流模型更适用于预测引射器性能,而Re-Normalization Group (RNG)k-ε和Realizablek-ε湍流模型则适用于优化引射器设计。文献[16]对引射器引射效率和摩尔回流率进行测试,验证了收敛型喷嘴引射器具有较好的工作性能。在引射器实验与仿真方法日益完善的基础上,如何提高引射效率作为引射器研究的核心问题受到学者们的广泛关注。文献[17]模拟引射器的全工况,发现流体质量流量会对引射性能产生较大影响,并给出工作流体质量流量的取值范围。文献[18]提出有关PEMFC氢气循环系统中收敛式喷嘴引射器几何参数的优化方法,并基于混合人工鱼群算法对引射器的几何参数进行优化。文献[19—20]研究了混合室收敛角对流量特性的影响,并给出混合室收敛角取值范围。
目前,燃料电池引射器的相关研究缺乏足够实验数据支撑,并且性能优化与特性研究方面仍不够完善。文中以车用PEMFC为研究对象,对引射器特性进行仿真与分析,在不同压力工况下采用计算流体力学(computational fluid dynamics,CFD)方法对引射器结构参数的影响规律进行仿真研究,基于仿真数据分析了关键结构参数与引射性能之间的关系,为引射器结构优化提供了数据和方法。
1 氢气供给系统
1.1 PEMFC基本原理
PEMFC主要由膜电极组件和双极板两部分组成,此外还包括密封件、集流板等[21]。双极板与膜电极构成了单体电池,应用中将单体电池固定于特定的密封装置中,利用端板压紧,使用螺杆等进一步固定,单体电池堆集组成燃料电池电堆。整体来看,燃料电池结构与三明治相似,中间为质子交换膜,两侧为催化剂层,氢燃料电池的催化剂层一般为铂基,向外与其相邻的是扩散层和双极板。PEMFC的工作原理如图1所示,膜层将其划分为阴极、阳极两部分,外回路导通,电池工作时扩散层内的反应气体扩散到催化层,气体燃料在催化作用下发生如下电化学反应。


图1 PEMFC的工作原理Fig.1 Working principle of PEMFC
进入电池阳极的氢失去电子,反应后产生的氢离子进入电解质,与进入阴极的氧气发生化学反应。电子则是经过外部回路到达燃料电池的阴极参与反应,最终生成水。整个反应伴随着热的产生。上述反应持续进行,电子不断地通过外部回路,完成发电。
1.2 氢气循环系统
PEMFC氢气循环系统见图2,在工作过程中,通过供应过量氢气的方法来保证输出功率稳定[22]。随着燃料电池内部反应的进行,电堆阳极废气中包含水和一定量未反应的氢气,利用水气分离装置将残余氢气分离出来并传输至引射器。引射器可利用高压氢气产生负压进而回收未反应的残余氢气,且不产生额外的寄生功率。供应的高压氢气从引射器喷嘴喷出后进入混合室,高速气流卷吸流动形成低压区,在压差的作用下,引射残余氢气与之进入混合室,均匀混合后从出口排出[17],参与电堆阳极反应。

图2 氢气循环系统的组成及相关器件Fig.2 Composition and related devices of hydrogen circulation system
1.3 引射器结构设计
文中采用索科洛夫引射器设计法,基于80 kW工况对PEMFC电堆进行结构设计[19,23]。工况参数如表1所示。根据电推参数求出引射器结构设计所需的工作流体质量流量GP后,即可结合工况参数,利用经验公式计算出引射器的结构尺寸[24]。结构参数包括工作流体喷嘴截面尺寸、等容混合室截面尺寸、引射器轴向尺寸等。

表1 设计工况点参数Table 1 Design operating point parameters
燃料电池正常工作时所需氢气量mH2可由式(1)求得。
(1)
式中:I为电池的工作电流;F为法拉第常数;Ncell为电池数目;i为电流密度;A为活化面积。
阳极入口水蒸气的质量分数ωH2O可由式(2)求得。
(2)
式中:XH2O为入口水蒸气的摩尔分数;H为氢气湿度。水蒸气在353 K温度下的饱和蒸汽压为47 414.7 Pa。
阳极入口气体质量流量min可由式(3)求得。
(3)
式中:mH2,in为阳极入口氢气质量流量;mH2为纯氢的质量流量;λ为氢气过量系数。
电堆的工作参数如表2所示,阳极入口氢气质量流量mH2,in即为用于引射器结构计算的工作流体质量流量GP。引射器结构参数的计算结果见表3。

表2 PEMFC电堆参数Table 2 Stack parameters for PEMFC

表3 引射器结构尺寸Table 3 Ejector structure parameters
2 引射特性建模及仿真
图3为引射器结构示意,文中采用ANSYS/CFX软件进行引射器的建模与仿真。选择引射系数μ作为引射性能的评价指标,定义为引射流体的质量流量与工作流体的质量流量之比[21],如式(4)所示。
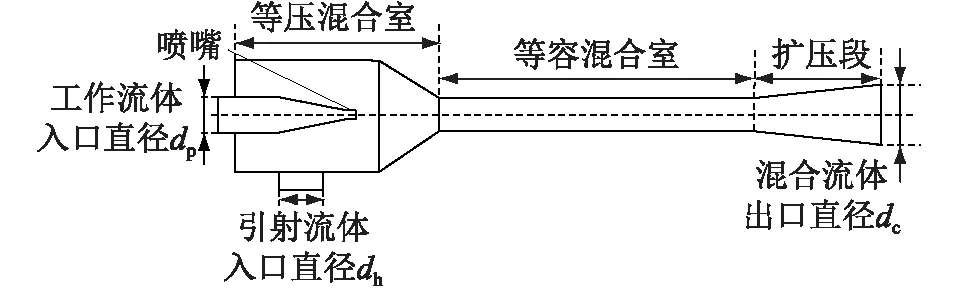
图3 燃料电池引射器结构示意Fig.3 Schematic diagram of fuel cell ejector

(4)
式中:GH为引射流体的质量流量。
2.1 控制方程
引射器的数值计算采用k-ε模型的修正方程,即RNGk-ε模型,基于N-S方程组的再归一化,能更好地预测引射器内部流动情况以实现结构优化。假设流体为稳态可压缩湍流,引射器管壁为绝热壁面,工作流体与引射流体均为理想气体,忽略重力影响且无化学反应发生,则引射气体控制方程为:

(5)

(6)

(7)
式中:ρ为密度;t为时间;U为速度矢量;k为湍动能;ε为湍动能耗散;μeff为有效黏度;p′为修正压力;B为体积力总和;T为热力学温度;μt为湍流黏度;σεRNG,Cε1RNG,Cε2RNG为系统常数。
2.2 网格划分
对于有限元分析来说,仿真精度和计算速度取决于模型网格划分质量的高低。对模型进行网格划分,初步划分后对模型边界区域、工作流体与引射流体接触混合区等处的网格适当优化加密,以保证模型网格划分的质量。最终通过网格无关性验证后的网格数量为1 100 764个。
2.3 边界及初始条件
引射器工作流体为理想氢气,进口边界条件按总压力进行设定;引射流体入口与混合流体出口的边界条件设定为恒定压力边界,具体设定值参照表1。流体的流态为稳态湍流,且为可压缩的理想状态。初始情况下,湍流强度为5%,温度为298 K,设定参数残差小于10-5时收敛[17,21]。
2.4 模型验证
为验证CFD模型的准确性,在工作流体入口压力4×105~6×105Pa范围内选择5个点进行仿真运算,得到引射器工作流体质量流量GP与工作流体压力pp的变化曲线,如图4所示。GP与pp在该范围内呈线性正相关,符合理论推导结果[23]。二者关系式可表示为如下形式:
Gp=kpp+b
(8)
式中:k,b为两定值。

图4 工作流体质量流量与入口压力的变化曲线Fig.4 Variation curve of working fluidmass flow and inlet pressure
3 结果与分析
3.1 内部流场分析
通过流体力学仿真得到引射器中间对称截面的压力、速度云图分别如图5、图6所示。工作流体喷嘴处压力势能转换为流体动能,工作流体速度在收敛喷嘴处迅速增大,变为超音速,压力值降至最低时喷嘴出口流体速度达到峰值。在高速射流的卷吸作用下,引射流体与之混合并发生动量交换,高速射流速度降低,引射流体速度增加。形成的混合流体经混合室后速度逐渐降低。通过图6可以看出,引射器中间对称截面的速度分布是非对称的,相应地计算出引射器轴线上的压力、速度变化。

图5 引射器中间对称截面压力云图Fig.5 Pressure cloud diagram of symmetrical section of ejector

图6 引射器中间对称截面速度云图Fig.6 Velocity cloud diagram of symmetrical section of ejector
图7为轴线上压力、速度分布曲线,引射器中气体流速在喷嘴处迅速达到峰值,之后随着距离的增加逐步下降,且在开口尺寸变化处存在一个拐点。相应地,工作流体压力在通过内部收敛喷嘴时压力骤降,出口附近压力值降至最低,在低压高速工作流体卷吸流动的作用下引射流体进入混合管,混合过程中压力缓慢上升,在扩散管减速增压的作用下,压力值最终恢复。

图7 引射器轴线压力和速度分布曲线Fig.7 Pressure and velocity distribution curves at the ejector axis
3.2 影响因素分析
引射器的结构参数对于流体特性有显著影响,进而产生不同的引射效果。以引射系数为评价指标,基于CFD模型进一步研究不同压力工况下引射特性的影响规律。
3.2.1 引射流体入口直径
引射流体入口压力ph分别取2.57×105Pa,2.77×105Pa,2.97×105Pa 3种工况进行分析,入口直径dh等间隔选取6个参考点,基于3种压力优化仿真以保证不同工况下结果的普遍性,仿真结果见图8。

图8 引射系数随引射流体入口直径变化曲线Fig.8 Variation curve of ejection coefficient with ejection fluid inlet diameter
可以看出,不同工况下曲线具有相同的变化趋势,引射系数μ随引射流体入口直径dh的增加单调增加,但变化率逐渐降低,最终趋于平稳。随着dh的增加,引射流体的吸入阻力变小,一定质量流量的工作流体可以吸入更多引射流体,并且入口尺寸的增加为引射过程提供足够的流体供应,引射系数相应增加。由于结构与流量的限制,dh增加到一定程度后不再引起引射性能的变化。此外,对比3条曲线可以看出,引射流体入口压力ph对引射性能有很大影响,μ随着ph增加而提高。由于压力的增加,入口与收敛喷嘴出口之间压差变大,工作流体通过剪切作用实现对更多量引射流体的卷吸,引射流体质量流量GH增加,引射系数提高。
3.2.2 工作流体入口直径
工作流体入口直径dp的变化会引起工作流体质量流量Gp的变化,进而影响引射性能。探究入口直径与引射系数的关系时,引射流体入口压力和混合流体出口压力保持设计工况不变,工作流体入口直径作单一变量,在6~14 mm范围取5个参考点仿真,3种工况下的分析结果如图9所示。可以看出,不同压力工况下的响应曲线都呈现先增后减的趋势,工作流体入口直径存在一个临界值。

图9 引射系数随工作流体入口直径变化曲线Fig.9 Variation curve of ejection coefficient with working fluid inlet diameter
3.2.3 混合流体出口直径
最后对混合流体出口直径dc进行仿真研究。工作流体入口压力pp和引射流体入口压力ph保持工况值,分别在混合流体出口压力pc为2.8×105Pa,3.0×105Pa,3.2×105Pa 的3种工况下进行仿真对比。混合流体出口直径dc为单一变量,在8~18 mm范围内取6个采样点,仿真结果如图10所示。可以看出,不同出口压力工况下,引射系数均随dc的增加先单调增加,达到某一临界值后开始减小,在3.0×105Pa和3.2×105Pa时,dc达到临界后引射性能下降速率迅速增加。随着混合流体出口压力的增加,引射器背压增加,阻碍了流体流出,引射系数减小,但引射系数对出口直径变化的敏感度降低,引射器工作性能的稳定性得到提高。

图10 引射系数随混合流体出口直径变化曲线Fig.10 Variation curve of ejection coefficient with the diameter of the mixed fluid outlet
3.3 引射效果分析
由上述分析结果可知,引射流体入口直径的增加可以提升引射性能,但存在一个拐点,在该拐点之后,提升效果不再明显;而工作流体入口直径与混合流体出口直径的影响则均存在一个峰值点,随着尺寸的持续增加,引射系数在到达峰值点之后开始迅速降低。根据上述分析结果对引射器结构参数进行优化,在各部分结构不发生干涉的前提下依次调整引射流体入口直径、工作流体入口直径和混合流体出口直径,使引射性能达到最优。优化后的结构参数对引射效果的计算如表4所示,可以看出,优化后引射流量提升了15.25%,引射系数提高了13.55%,改善了相同条件下未反应氢气的循环利用率。

表4 优化前后引射效果对比Table 4 Comparison of injection effect before and after optimization
4 结论
文中针对电动汽车PEMFC氢气循环系统进行了引射器工作特性研究与建模,基于计算流体力学仿真探究了引射器内部流场特性,揭示了不同压力工况下引射流体入口直径、工作流体入口直径及混合流体出口直径对引射系数的影响规律,得到以下结论。
(1) 引射系数与引射流体入口直径呈正相关,但随着入口直径的增加,引射系数的提升量逐渐降低且在入口直径14 mm附近存在拐点;
(2) 工作流体入口与混合流体出口参数对引射系数的影响存在一个峰值点,在峰值前后均呈现先增后减趋势;
(3) 通过优化,引射流量提升了15.25%,引射系数提高了13.55%。可见,在相同条件下未反应氢气的循环利用率得到了显著改善。

