轻骨料混凝土单轴受压应力-应变关系研究综述★
杨 滢,李琮琦,刘虎山,吴 昊,陈 波,方 润
(1.扬州大学建筑科学与工程学院,江苏 扬州 225127;2.江苏和天下节能科技有限公司,江苏 扬州 225127)
1 概述
轻骨料混凝土(Lightweight Aggregate Concrete,简称为LAC)是用轻粗骨料、砂、水泥及水制备而成,干表观密度低于1 950 kg/m3的混凝土[1]。与传统普通混凝土相比,LAC拥有结构效益好、保温隔热效果好、自重轻、经济环保性优良、综合经济效益显著的特点;尤其是运用于装配式建筑时,相较于传统混凝土具有较大优势。因此,从20世纪50年代开始,轻骨料混凝土的制备与应用逐渐被各国重视并发展。然而,轻骨料混凝土由于骨料脆性大,强度低,在使用过程中容易出现建筑物开裂的问题[2-3],因此,对其进行单轴受压下应力-应变关系的研究很有必要。
本文围绕轻骨料混凝土的受压性能及其影响因素,基于近20 a来国内外学者的研究成果,从轻骨料混凝土单轴受压受力特点、弹性模量及峰值应变数值模型、本构关系、受压性能影响因素等方面进行概述,并提出有待深入研究的问题。旨在吸引更多学者关注轻骨料混凝土的基本力学性能研究,使轻骨料混凝土得到更广泛的工程应用。
2 轻骨料混凝土单轴受压全过程及其特点
轻骨料混凝土应力-应变间的关系即本构关系,本构关系是混凝土材料的基本特性,它关系着构筑物的内力分布、变形大小、抗震性能等。魏慧[4]等学者的研究表明,LAC与普通混凝土的单轴受压破坏过程十分相似,应力-应变曲线同样存在四个阶段:弹性变形阶段、裂缝出现阶段、裂缝发展阶段、残余强度阶段。
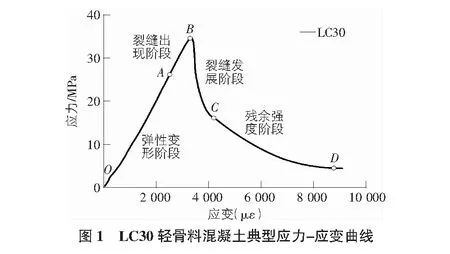
多位学者研究的轻骨料混凝土单轴受压应力-应变关系曲线如图1所示(以LC30为例)。各阶段的受力特征[5]如下:
1)OA段:弹性变形阶段,此时应力与应变之间表现为线性关系,曲线斜率反映混凝土的弹性模量,而LAC的弹性模量略小于同等级的普通混凝土。
2)AB段:裂缝出现阶段,此时,应力增长处于稳定期,应变增长速率加快,曲线斜率开始缓慢减小,试件刚度开始退化。
3)BC段:裂缝发展阶段,与普通混凝土相比,LAC内部薄弱面较多,试件裂缝数量增长较快,且增长不断加快,达到峰值应力后,应力下降迅速,试件呈脆性。
4)CD段:残余强度阶段,随着应变的持续增加,应力下降速率缓慢,此时大部分荷载由裂缝间残余粘结力及摩阻力来承担,承载力为峰值荷载的60%左右。
LAC与普通混凝土相比,除了拥有结构效益好、经济环保、性能优良等优点外,还存在脆性大、易产生裂缝的缺点,因此,在对LAC应力-应变关系进行研究时,应当更关注对于其延性与韧性的改善。
3 轻骨料混凝土单轴受压弹性模量与峰值应变数值模型
3.1 弹性模量
一般情况下,LAC的弹性模量(Ec)会比同级普通混凝土低,其主要影响因素为混凝土强度等级(fcu)和表观密度(ρ),弹性模量(Ec)随着强度等级的增大而增大,试件尺寸和骨料类型等因素对其影响较小。
对于LC15~LC60、密度等级1 200 kg/m3~1 900 kg/m3的轻骨料混凝土,JGJ 51—2002轻骨料混凝土技术规程[6]提出的数值模型如式(1)所示:
(1)
李平江[7]以高强页岩陶粒为原料,配制出混凝土强度26 MPa~68 MPa、密度在1 750 kg/m3~1 960 kg/m3的轻骨料混凝土,并进行弹性模量的数据分析,提出弹性模量的数值模型,如式(2)所示:
Ec=2.13ρ(fcu)0.5
(2)
3.2 峰值应变
众多学者认为,轻骨料混凝土应力-应变曲线的峰值应变(εc)随着受压试件强度等级(fc)的增大而增大,并建立了εc与fc之间的函数关系。
对于低强度的普通混凝土及轻骨料混凝土,过镇海[8]提出如下统一计算式:
εc=(1 637+20.4fc)×10-6
(3)
王振宇[9]结合8组实验数据以及已有结论,建议适用于轻骨料混凝土单轴受压曲线峰值应变的公式:
εc=(1 788+17.48fc)×10-6
(4)
丁发兴[10]基于过镇海和王振宇建立的公式,通过对国内学者大量的试验数据进行分析,建议了轻骨料混凝土应力-应变峰值应变的经验计算式:
εc=760fc×10-6
(5)
国内外学者对于LAC的弹性模量及峰值应变数值模型都有大量研究,弹性模量的主要影响因素为混凝土强度和表观密度,峰值应变的主要影响因素为混凝土强度,但对于一些次要影响因素下的研究(如截面形状、养护方式等)还较少,导致数据具有一定离散性。
4 轻骨料混凝土单轴受压本构模型
在大量试验资料的基础上,众多学者基于不同强度等级、不同材料等影响因素的轻骨料混凝土单轴受压应力-应变全曲线提出了半经验-半理论的数值模型。
T.H.WEE[11]以水胶比、掺合料、龄期为影响因素,进行了163个强度为50 MPa~120 MPa混凝土试件的应力-应变全曲线试验,并提出高强混凝土本构数值模型,如式(6)所示。
(6)
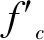
过镇海等基于低强度普通混凝土及陶粒混凝土的13组数据的分析,提出了分段式全曲线方程,建议了混凝土单轴受压应力-应变的数值模型,如式(7)所示。
(7)
其中,参数αa为初始弹性模量和峰值割线模量的比值,1.5≤αa≤3.0;参数αd与混凝土强度等级和约束方式有关,αd≥0。
王振宇等对LC30~LC55的5组轻骨料混凝土进行试验,提出了适用于过镇海公式的LC10~LC55全曲线参数,其中LC50未获得下降段数据,并提出由于LC55级轻骨料混凝土很脆,上升段采用过镇海提出公式的形式,下降段曲线拟合应采用分段的形式,如式(8)所示。
(8)
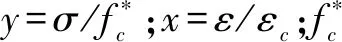
丁发兴等基于王振宇的轻骨料混凝土应力-应变曲线实验数据以及余志武[12]建议的全曲线表达式,通过数值积分和拟合回归,提出无量纲形式的数值模型方程,如式(9)所示。
(9)

美国学者P.T.WANG[13]通过对试验设备改进,解决了试验设备本身刚度较小的问题,通过对抗压强度为21 MPa~56 MPa的轻骨料混凝土和抗压强度为21 MPa~77 MPa的普通混凝土进行了应力应变分析,指出轻骨料上升缓慢,下降迅速,并提出式(10)。
(10)
其中,X=ε/ε0,ε为混凝土的应变,ε0为曲线的峰值应变,Y=σ/f0,σ为混凝土的应力,f0为曲线峰值应力。曲线分上升段和下降段,上升段和下降段由四个不同常数A,B,C,D,控制不同强度等级的四个常数各不相同。
LAC由于骨料脆性大,在应力-应变试验中下降段较难获得,尤其是当LAC的强度增大时,脆性特征更显著,因此,高强LAC的应力-应变曲线数据仍是未来研究的重点。同时,由于现代科技的发展,人类生活水平的提高,为满足实际工程应用中构筑物韧性的要求,纤维增强LAC的应力-应变关系数值模型的研究也是一大趋势。
5 结语
轻骨料混凝土结构效益好、经济环保性优良,在现代建筑中尤其是装配式建筑中具有良好发展前景,为了更加深入的研究其单轴受压下应力-应变关系,系统分析内力分布、变形大小,改善轻骨料混凝土在使用过程中脆性大易开裂的问题,建议加强高强轻骨料混凝土应力-应变关系的研究,探究多种混杂纤维对轻骨料混凝土的增韧阻裂效果,完善轻骨料混凝土应力-应变关系的数值模型,同时考虑多因素共同作用下的应力-应变关系,如潮湿低温环境、海水侵蚀环境、高温火灾环境等。

