基于区域划分和余弦定理的DV-Hop算法改进

费辰阳，邵树金，邢竹萍，潘幼岳，张爱清

(安徽师范大学 物理与电子信息学院，安徽 芜湖 241000)

0 引言

无线传感器网络(Wireless Sensor Networks,WSN)是一种分布式传感网络，网络中的传感器通过无线方式通信，网络配置灵活。基于这些特点，无线传感器网络对人类生活和社会进步起到很大的作用。由于无线传感器网络需要对环境进行监测、探测和采集数据等，这些都需要包含定位信息，因此，定位技术是无线传感器网络的关键技术之一。

无线传感器网络定位算法分成两个大类：无需测距(Range-Free)定位算法和基于测距(Range-Based)的定位算法。无需测距定位技术不需要直接测量距离和角度信息，而是通过对节点间的距离进行估计或者确定包含未知节点的可能区域来确定未知节点的位置。无需测距定位算法主要有质心定位算法(Centroid)、距离向量-跳段定位算法(Vector-Hop,DV-Hop)、近似三角形质心定位算法(Approximate Point-in-Triangulation Test,APTI)等。质心定位算法位置估计精确度和信标节点的密度、分布有很大关系，DV-Hop定位算法利用多跳信标节点信息来参与节点定位，APTI定位算法通过计算包含目标节点所有三角形的重叠区域，并求解质心来进行定位。这些算法或多或少都存在一些缺陷和问题，导致定位的精度不高。其中DV-Hop算法因对节点的硬件要求低、实现简单等优点被广泛应用，但由于其定位精度受节点分布的影响，在有些场景中定位误差比较大。

针对 DV-HOP 在节点随机分布的网络环境下存在较大误差的问题，已取得了一些研究成果。文献[1-4]均提出通过RSSI测距优化节点间的跳数来减小定位误差。其中，文献[1]算法提出：首先利用节点间RSSI值与基准RSSI值的比值量化节点间跳数，使整数跳数转化为连续跳数，并在量化跳数的基础上对信标节点平均跳距进行重估，然后对各信标节点平均跳距进行加权处理以修正未知节点平均跳距，最后利用未知节点与最近信标节点的距离关系对未知节点坐标的估计误差进行修正。文献[2]在RSSI测距优化节点间的跳数的基础上，使用校正因子修正DV-Hop算法中的平均跳距，并采用无约束优化算法代替传统的最小二乘法来计算未知节点坐标。文献[3]研究的RADV-Hop算法引入RSSI进行跳数分级来修正节点间跳数，并基于最小均方准则修正跳距。文献[4]利用RSSI测距技术,定义信标节点的平均跳距误差,并利用信标节点的平均跳距误差对未知节点与信标节点之间的距离进行修正。文献[5-6]均提出通过余弦定理来调整估计跳距；文献[7-8]的核心思想是优化信标节点的部署，为一定范围内的未知节点合理分配最优信标节点，进一步提高定位进度；文献[9-10]提出采用基于加权重值的最小二乘法来计算未知节点的坐标。结合以上算法的优点，本文提出基于区域划分和余弦定理的DV-Hop改进算法(Region Division and Cosine Theorem improving DV-Hop,RDCTDV-Hop)，提高定位精度。

1 DV-Hop算法误差与分析

1.1 DV-Hop定位技术

DV-Hop算法实现步骤为：

① 计算未知节点与每个信标节点的最小跳数：使用经典距离矢量交换协议，每个节点维护一个表(x,y,h)，其中x，y，h分别代表信标节点坐标和到该信标节点的跳数。每个信标节点发送一个包含自身位置信息和跳段个数的广播分组，跳段个数初始化为0。节点收到信标节点的广播分组后，检验分组跳段数是否小于节点表内的存储值，是则更新该表，然后跳段数加1并广播该分组，否则丢弃该分组。最终所有的未知节点均能获得距离每个信标节点的最小跳数。

② 计算未知节点与信标节点的距离：每个信标节点根据自身表中记录的其他信标节点的坐标信息和跳数，按照式(1)计算出平均跳段距离并将其利用可泛洪法进行广播，每个节点均只接收第一个跳段距离，忽略后来到达的，确保绝大多数节点可以从最近的信标节点接收平均跳段距离。最后未知节点可计算自身到达相应信标节点的距离。

平均跳距计算公式为：

式中，(xi,yi)，(xj,yj)为节点i,j的位置坐标;hopij为节点i和j间的跳数距离。

未知节点到信标节点计算公式为：

dij=Average×hopij。

当节点分布如图1所示时,各段距离具体计算如下：

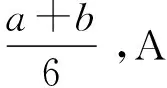
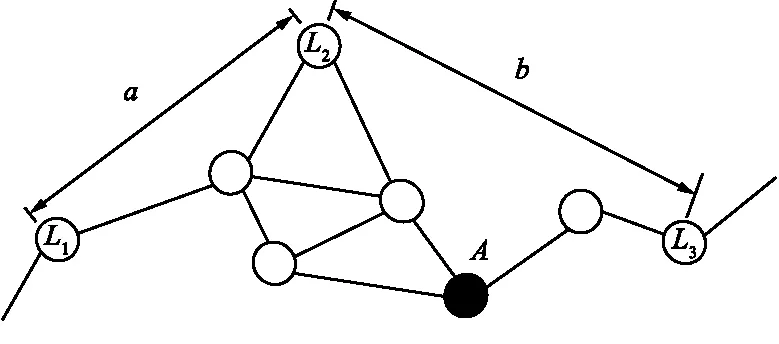
图1 节点分布1Fig.1 Node distribution 1

③ 未知节点通过三边定位或多边定位算法计算自身的坐标。

1.2 误差分析

第一阶段，由于传感器节点都是随机分布，分组在被广播的过程中可能存在冲突素，节点得到信标节点的最小跳数存在一定偏差，且跳数越多，偏差越大。

第二阶段，估算平均跳段距离时，利用的是除本节点外所有其他信标节点，所以得到的是全部范围内的平均跳距离，不能反映局部范围内的网络密度分布情况。此外，如图2所示，信标节点间客观存在空间方位，节点间因为存在角度而产生误差。在实际测量中这种情况很容易出现，尤其是在节点密度较大时这种情况发生的可能性也会更大。

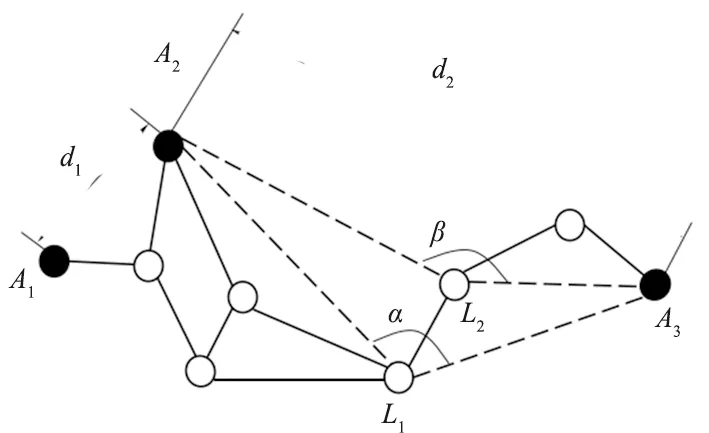
图2 节点分布2Fig.2 Node distribution 2

第三阶段，分布密度的不均匀导致信标节点距离方差较大，尤其是在信标节点密度较小时，信标节点间距离的方差会更大，出现的误差也会越大。另外，每个节点间的距离都不固定，跳数是非连续跳段，当按照平均跳段距离和跳数估计距离时，存在较大误差。

2 RSSI分级跳数

2.1 误差分析

在经典DV-Hop算法中，未知节点只保留最先接收到的平均跳段距离，这个平均跳段距离往往来自于距其最近的信标节点。这将导致单跳距离产生的误差较大，如图3所示，会导致实际距离与估测距离之间的偏差较大，从而影响未知节点的定位精度。

图3 单跳误差示意图Fig.3 Schematic diagram of single hop error

对于相距未知节点较近的信标节点，由于它们之间的跳数较少，每跳产生的误差能够相互抵消的可能性较更小，当误差相互叠加后会使得估计距离与实际距离之间的偏差更大。

对于相距未知节点较远的信标节点，他们之间的跳数足够多，误差在累加的过程中能够相互抵消的可能性较大。但由于未知节点与信标节点相距较远，而未知节点所获取的平均跳段距离是由其临近节点提供的，所以如果仍然用这个平均跳段距离去计算，显然会存在较大误差。

2.2 RSSI跳数分级原理

参考文献[1-2]中指出，为了减小由跳数引起的误差，可采用RSSI测距对跳数进行分级改进的思路。在减小每跳实际距离与平均跳段距离误差的同时也可以增加跳数，使每跳误差在累加过程中能够相互抵消的可能性增大，令估测距离更加接近实际距离。

RSSI测距技术的原理是：根据发送端到传输端之间的信息传输功率损耗，在一些特定损耗模型的基础上，接收端由损耗功率估算出信息传输距离。其中较为常用的信号传输模型是对数-常态分布模型，根据文献[1]具体可分为两种：Pass Loss模型和遮挡因子模型。

Pass Loss模型：

(1)

式中，P(d0)和P(d)分别表示与发送端相距d0和d处接收端收到的信号功率，η为路径损耗因子，通常取值在2～4，由此可以通过接收功率的大小与参考距离的接收功率进行比较进而估算出距离。

遮挡因子模型：

(2)

式中，相距发送端d0和d的接收功率用分贝表示即[P(d0)]dB和[P(d)]dB。Xσ为遮挡因子，是平均值为0的高斯分布变量，其描述了接收信号强度随距离的变化关系，即表示信号功率本身随距离的变化与环境因素无关，也可以用信号的发射功率[Pt]dB表示，同时还可以将式(3)看做信号传输过程中的路径损耗，用[PL]dB表示，则式(2)可以表示为式(4)：

(3)

[P(d)]dB=[Pt]dB-[PL]dB。

(4)

假设将一跳划分为g级，根据文献[3]取节点的通信半径做为参考距离d0，可由式(2)通过接收信号的功率确定分级后的跳数。其判断规则如下：

若某节点接收到的功率[P(d)]dB满足式(5)，则该节点到发生信号节点间的跳数为i/g。

(5)

节点i到j间的总跳数hij可以表示为：

(6)

式中，n表示节点i到j的节点总数。

3 基于节点密度的算法改进

3.1 误差分析

在一定的区域范围内，节点密度越高该区域的节点分布相应会更均匀。而在DV-Hop算法中，节点分布越均匀，其误差越低，定位精确度越高；节点分布越不均匀，其误差也就越高，定位精确度越低。

当节点密度较高时，由于其物理属性产生的误差将会升高而无法忽略，从而增加其整体定位误差，降低定位精确度。

以下算法对上述两条误差来源进行矫正。

3.2 余弦定理矫正平均跳距

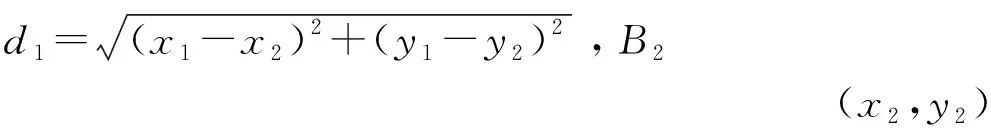
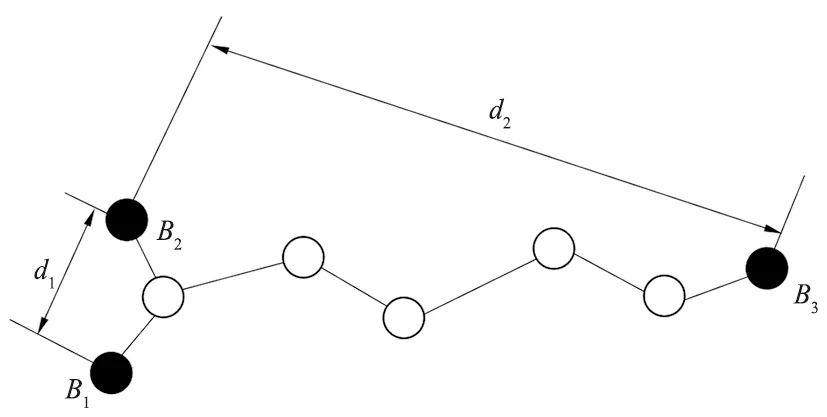
图4 传感器网络节点结构Fig.4 Node structure of sensor network

3.2.1 中间节点的选择

根据连接到每个信标节点的最小跳数的传输路线，将路线中间的节点作为中间节点，设Jp_Num为节点间的跳数。

当Jp_Num为奇数，选择路线的中间节点，如图5(a)所示；当Jp_Num为偶数，选择路线中间的两跳都作为中间节点，其中α、β为中间节点与两端信标节点之间连线所形成的夹角，如图5(b)所示。

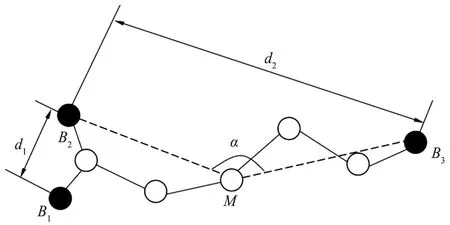
(a) 信标节点B1与B3之间跳数为奇数

设dHopB2为利用余弦定理所求出的平均跳距。结合图5(a)可证明，当Jp_Num为奇数时，计算公式为式(7)；由图5(b)可证明，当Jp_Num为偶数时，计算公式为式(8)。

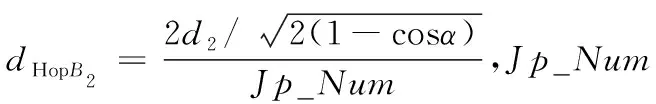
(7)

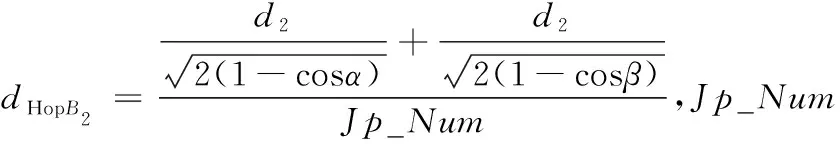
(8)

3.2.2 夹角范围的证明

角度与传输路径示意如图6所示，节点A、B之间有两条路线，分别是A-C-B和A-D-B，由几何关系可知A-C-B比A-D-B路线更短，更加接近AB的值，而α>β，且α更接近180°。由三角形三边关系可知，当α越接近180°时，A-C-B的距离越接近AB，所要绕行的路线更短，而使用传统DV-Hop测距得到的平均跳距误差也就越小。

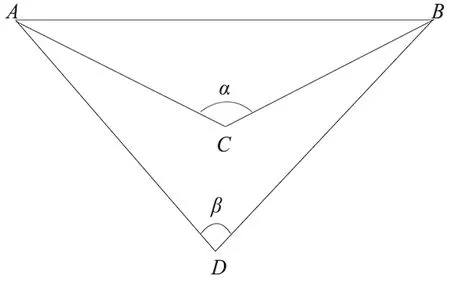
图6 角度与传输路径示意图Fig.6 Schematic diagram of angle and transmission path

3.2.3 余弦定理求校正值

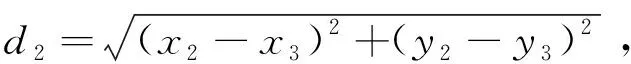
(9)

可使用校正值对传统法计算的平均跳距进行校正，减少误差。

3.2.4 适用条件

由概率知识可知，在一定区域内，由于节点间的坐标各不相同，当该区域内节点数量越多时，传感器的排列情况越少，分布越均匀，若不考虑节点间的空间夹角，则随着节点数量的增加，传统算法所得到的平均跳距越准确，误差越小。

本文提出的改进策略可以减少节点非直线分布造成的误差，且该算法的误差随节点密度增加而减少。

3.3 区域划分

3.3.1 划分算法

根据参考文献[7-8]中的移动信标算法，本文设计出区域合并的算法。根据节点密度越大，误差越小的结论，DCMDV-Hop算法采用先区域划分再对未知节点进行计算处理的方法，对传统的DV-Hop算法进行改进，使其节点密度较小区域的误差得以降低，从而降低其整体误差。

具体方案如下：将整个无线传感器网络所占地区的面积平均分成几等份(如图7所示)，先进行预划分，然后计算出各个面积中所包含的节点总个数。节点个数最多的两个区域合并(图7(b)中的a和b两个区域)，并计算出其中的未知节点坐标。将已知区域同剩余区域中节点个数最多的区域(图7(b)中的区域c)合并，再计算未知节点坐标。剩余的未知区域用以此类推的方法进行计算，如图8所示，直到计算出所有的未知节点坐标(合并的区域不一定相邻)。

(a) 划分前的区域示意图

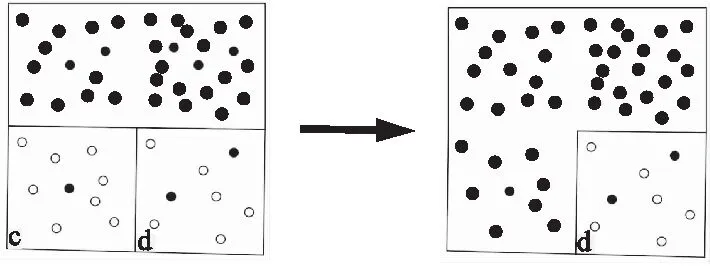
图8 区域合并Fig.8 Region merging

3.3.2预划分

在具体实施算法之前，需要对区域进行预划分来判断点是否在区域内。如图8所示，具体步骤如下：

① 使用均分面积形状的原则，预先设定划分规则，得到子区域；

② 基于无线传感器通信半径一定的原理，通过预发送代理数据包得到可能在所划分区域中的未知节点；

③ 根据参考文献[8]，可使用RSSI测距技术，排除在步骤②中所得到未知节点中不属于此区域的未知节点，得到此区域中的未知节点；

④ 在每个区域中重复步骤②～③过程，得到所有区域中的未知节点。

4 未知节点的坐标估算

设未知节点Ui到信标节点Bk的距离可用式(10)表示，hik为两个节点间的最小跳数：

dik=Hopsizek×hik。

(10)

假设n个信标节点的坐标分别为(x1,y1),(x2,y2),…,(xn,yn)，未知节点到各个信标节点的距离为d1,d2,…,dn。若未知节点Ui的坐标为(x,y)，则可由两点间距离公式求得n个方程组合的一组矩阵：

根据参考文献[9-10],未知节点的坐标可用最小二乘法来计算：

X=(ATA)-1ATb。

5 DCMDV-Hop算法实现步骤

DCMDV-Hop算法针对 DV-Hop 算法定位精度比较低的缺点，引入 RSSI 对跳数进行量化分级处理，使用余弦定理减少在节点密度过大时因空间角度导致节点路径曲折过多而引起的误差，同时引入区域划分思想减少在节点密度较小区域的误差。DCMDV-Hop算法实现步骤如下：

① 网络初始化。启动无线传感器网络，生成坐标矩阵。

② 使用RSSI分级计算跳数。根据能量衰减规律，测得节点间的大致距离，使用分级量化方式测算跳数，降低跳数误差。

③ 预划分区域。使用预划分算法，设置规则对当前需要定位的未知节点进行区域划分，为后续定位做准备。

④ 区域划分算法。使用划分算法，依次对预划分后所得子区域中的未知节点进行定位。

⑤ 平均跳距计算。使用传统DV-Hop算法得出各个子区域中未知节点的平均跳距，为了降低因无线传感器的物理属性对平均跳距所造成的误差，运用余弦定理矫正算法，使用式(9)对各个区域中所求得平均跳距进行矫正。

⑥ 最小二乘法估算未知节点坐标。

⑦ 将计算出的未知节点作为信标节点应用于下一子区域中，计算出其未知节点的坐标。

本文算法流程如图9所示，与传统 DV-Hop 算法相比，该算法在确保节点间估计距离误差较小的同时，不增加网络的通信量，提高了节点的定位精度。

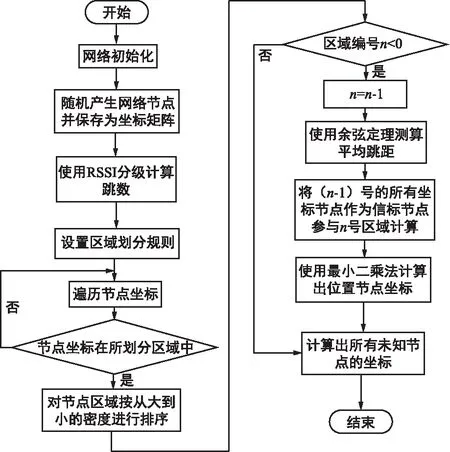
图9 DCMDV-Hop算法流程Fig.9 DCMDV-Hop algorithm flow chart

6 实验仿真

6.1 仿真环境及参数说明

仿真实验在MatlabR2019b环境下进行，仿真参数如表1所述。

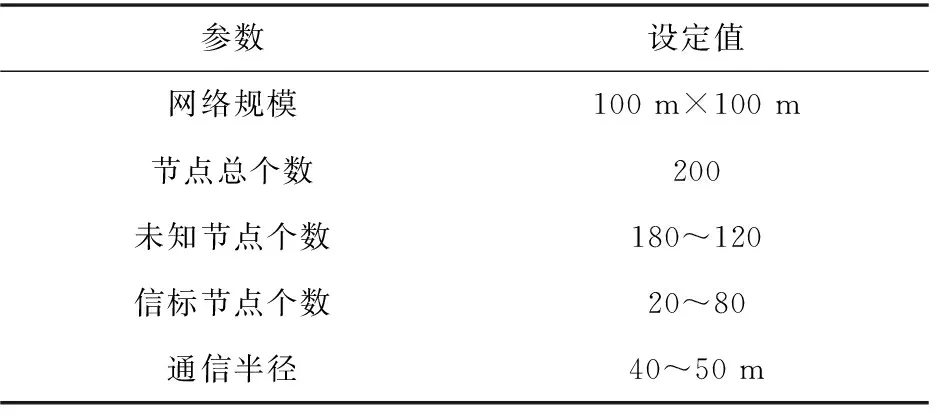
表1 仿真参数说明

模拟无线传感器网络场景为二维平面区域，节点分布如图10所示。其中红色“*”为信标节点，黑色“·”为未知节点。在面积为100 m×100 m的正方形区域内随机分布200个节点。考虑到节点的不确定性，本实验采取多次仿真取平均值。

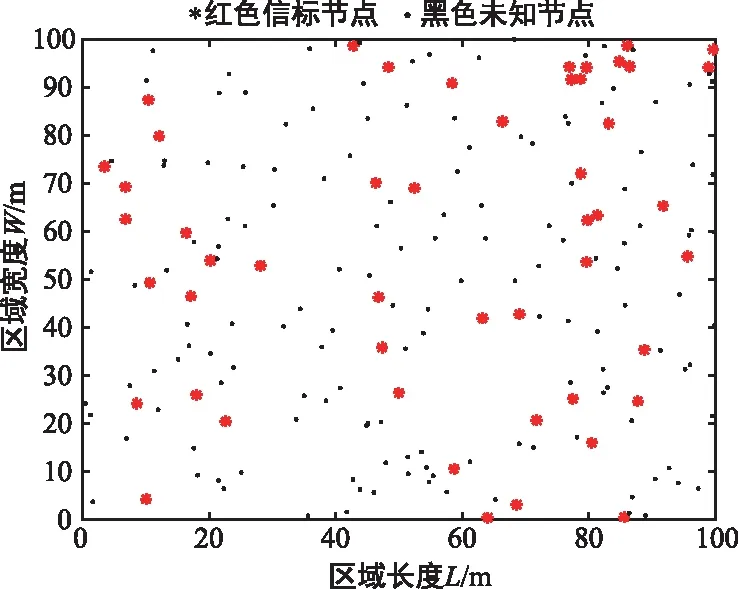
图10 模拟场景节点分布Fig.10 Distribution of nodes in simulated scene

6.2 仿真实验分析

使用Matlab对DCMDV-Hop算法进行仿真以寻找其定位误差规律。

① 本文使用了4区域划分与6区域划分在通信半径50 m与40 m的实验环境下，对节点定位误差与节点个数之间的关系进行了研究，仿真结果如图11所示。

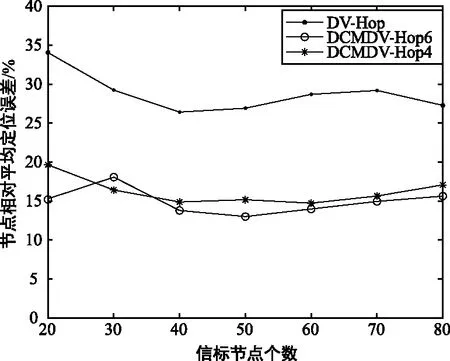
(a) 通信半径R = 50 m时

当信标节点个数上升时，由于信标节点密度上升使得信标分布更加均匀，进而减少平均跳距误差，但当信标节点个数较多时，节点实际存在的相对位置对平均跳距所产生的误差将不能被忽略，导致误差会再次开始增加。

② 信标节点密度对使用DCMDV-Hop算法所划分出的各子区域未知节点定位精度的影响对比分析如下。

本实验将整个区域分成6个部分，各自的节点相对平均定位误差如图12所示。

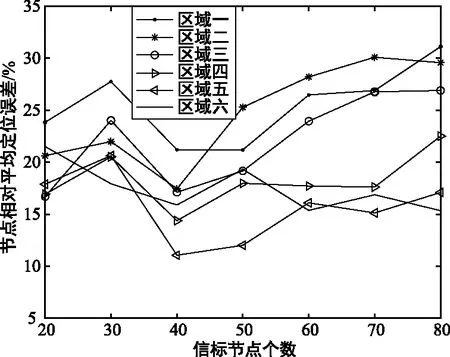
图12 6个子区域误差比较Fig.12 Comparison of errors of six sub-area

由图12可知，起始计算的区域由于信标节点密度逐渐上升,使得节点分布更加均匀，误差逐渐降低，但每计算一个区域得到未知节点坐标应用于下一区域的计算时,都会累计一定的误差，此误差使得计算得出的未知节点与信标节点的距离同其坐标不匹配，导致后面的区域误差逐渐上升。

从仿真结果可以看出，DCMDV-Hop与传统的DV-Hop相比，定位误差有明显减少，但由于各区域信标节点数量的不确定性，以及前面区域的坐标误差会对后续区域坐标计算有所影响，导致其整体定位稳定性有所下降。

7 结束语

针对DV-Hop在节点定位中所存在的不足之处，本文从三方面进行改进：① 使用对信标节点按照一定原则划分，增加其每一部分的均匀度以减小跳距跳数的误差；② 在节点密度较大的子区域中，由于节点密度过大会使节点间空间角度路径曲折过多，令这些误差较大而无法被忽略，可以使用余弦定理算法降低这一误差；③ 使用多通信半径减少传统DV-Hop，不考虑节点间距离实际情况使用单一跳数划分原则下，所造成的误差。由以上仿真结果可知，对比传统DV-Hop，本文提出的DCMDV-Hop算法定位精度有较大提升，且在规模较大的节点网络中拥有更大的提升。但本文的改进算法依然存在不足之处：在仿真运行时，该算法运行效率明显低于传统DV-Hop，通信开销较大。进一步研究算法以降低其通信开销，提升运行效率是以后研究工作的重点。