考虑焊接缺陷对双金属带锯条锯齿切削性能的影响研究*
李 磊 , 吴利平 , 钱 靖 , 刘 惺 , 郝红梅 , 邹修敏 , 陈 丽 , 卢学天
(1.四川化工职业技术学院机械工程学院,四川 泸州 646300;2.四川铁道职业学院城市轨道交通学院,四川 成都 611730)
0 引言
双金属带锯条(以下简称带锯)是由高速钢(齿部)和弹簧钢(背部)通过电子束或者激光焊焊接后,再经过一系列冷、热加工工艺制造的锯切工具。与其他锯切工具相比,具有锯切效率高、切割尺寸范围大、断面精度高等优点,因此被广泛应用于制造业中,尤其是备料工序阶段。近年来,随着被加工材料的性能不断改善以及各制造企业对生产成本的控制加大,企业对加工刀具的切割效率和使用寿命等方面提出了更高要求[1]。基于此,相关的学者们对带锯进行了深入研究。Sarwar M、Haider J等[2]分析了带锯条的铣齿工艺,因齿尖毛刺较多而影响带锯寿命。Lengoc L等[3]、Gendraud P等[4]研究了锯条寿命和振动之间的关系。朱维斗[5]分析了带锯崩齿的原因。匡旭光等[6]研究了表面干喷工艺对带锯性能的影响,得到干喷提高带锯寿命的结论。陈刚等[7]研究了双金属CO2激光焊接工艺。贾寓真等[8]通过锯切GCr15和空转疲劳测试,对比了表面喷砂工艺对双金属带锯条疲劳寿命的影响。卫寿亮等[9]对带锯激光焊表面缺陷进行了分析,提出降低气孔形成率的焊接方案。柳艳等[10]对M42-X32双金属带锯进行了回火工艺研究,分析了其硬度下降和寿命提高的原因。李贵茂等[11]对双金属带锯条进行了淬火处理的研究。刘国跃等[12]分析了带锯齿距和切削力的关系。
综上所述,这些研究主要集中在带锯的齿形设计、振动机理、制造工艺等方面,对带锯的制造和寿命起到了较大的促进作用,为带锯寿命的试验研究提供了设备基础和理论支撑,但影响带锯寿命更为重要的焊接工艺方面的研究主要是基于锯切实验进行的,此类研究周期较长、成本较高并且需要专用的试验设备。这严重影响了我国带锯走向高端产品市场的进程,因而缩短此类研发的周期、降低研发成本,从带锯制造过程中的工艺缺陷对带锯寿命和切削性能的影响机理进行研究,成为目前带锯研发中亟待解决的问题之一。
课题组提出考虑含焊接工艺缺陷的锯齿切削力数学模型,并将焊接缺陷中典型焊缝裂纹等因素进行参数化,通过改变缺陷参数,计算切削力,从而得到了“焊接缺陷-切削力”的变化趋势。
1 单个锯齿切削力数学模型
1.1 锯齿切削力模型
双金属带锯条结构如图1所示,由弹簧钢和高速钢焊接而成。双金属带锯条由多个锯齿循环一组组成变齿形带锯条,一般用TPI[12]表征,其齿形根据结构可分为通用齿形、抗拉齿形、龟背齿形等。
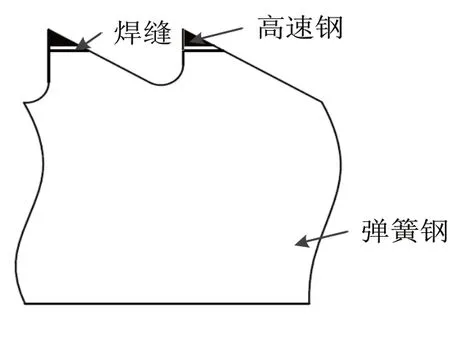
图1 双金属带锯条示意图
由于其切削过程中,相当于每个单独锯齿进行切削,而每组锯齿中,单个锯齿受力较为类似,因此,在不考虑分齿、变齿的情况下,将单个锯齿进行简化,可将其简化为悬臂梁,裂纹分为中心裂纹、边裂纹、表面裂纹等。本文以贯穿裂纹为例进行计算,单个锯齿力学模型如图2所示。

图2 单个锯齿力学模型
其中,F为单个锯齿的受力;H为双金属锯条崩齿断裂处的长度;h为焊接裂纹尺寸;△y为裂纹中心到锯齿中心的距离;y1为焊缝左边部分中心到锯齿中心的距离;y2为焊缝右边部分中心到锯齿中心的距离。
1.2 考虑焊接缺陷的数学模型
双金属带锯条在切削过程中,锯齿断裂是其中一种失效形式,而当其在制造过程中存在焊接缺陷时,可能会造成锯齿的崩刃。由于切削力主要和切削速度、材料等参数有关,因此,用锯齿切削力不易表示单个锯齿切削性能,考虑其崩刃前的瞬间,是达到了断裂的强度极限的。若存在裂纹,则危险截面即为焊接裂纹所在位置。单个锯齿简化为悬臂梁模型后,其裂纹所在截面为弯矩最大的地方,因此考虑其弯曲应力σ,以此来表征锯齿的切削强度极限。
由材料力学弯曲应力可知:

式中:σ为锯齿根部的弯曲应力;M为最大弯矩,y为最大弯矩发生处到中性轴的距离,Iz为截面对z轴的惯性矩,[σ]为需用应力。
图2 结构中的参数y1、y2分别为:

将y1、y2代入式(1),得焊缝两端的应力分别为:

当焊缝中心处于图1所示位置时,由式(3)可知,σ1>σ2,反之则σ2>σ1;以图1中位置为例,推导其“F-h”数学模型为:

当双金属带锯条确定后,式中b、H、h、L、[σ]为常数,因此,用Fφ替代,则得到切削力的极限力F与焊缝h的关系为:

其中,Fφ为:

2 焊接缺陷对切削力的影响分析
2.1 裂纹大小对单个锯齿切削力影响分析
由于式(5)并非简单的线性或规则的“F-h”关系,因此,以某型号双金属带锯条为例,探究当裂纹位置确定时,裂纹大小对极限力的影响。相关参数如表1所示。

表1 双金属带锯条相关参数
分别取△y为0、0.02 mm、0.05 mm、0.1 mm、0.15 mm、0.2 mm,将h由0开始取值,以0.01 μm为步长,分别计算极限力F,并绘制“F-h”图像,如图3所示。
由图3可知,观察某一曲线,当裂纹中心偏移量△y一定时,极限切削力F随裂纹大小h的增大而减小,并且呈现二次函数下降关系。根据文献[12],当单齿切削深度为20 μm,切削力Fc≈80 N,即此时单个锯齿需要提供超过80 N的力,才能满足切削要求,

图3 F-h关系图
而单个锯齿切削深度增加2倍时,切削力增大1.3倍。考虑力学模型忽略变齿和分齿的影响,因此,引入影响系数n,则极限切削力F为:

用极限切削力F来表征单个锯齿的切削性能,即当双金属带锯条在切削过程中,如果正常工作,则切削力Fc为一确定数值,若出现崩齿,则说明此时该齿能承受的极限力达不到切削要求,因此,可以用单个锯齿能承受的极限力来表征切削性能。极限切削力F越大,实际切削过程中,越不容易崩齿。
由式(7)得,当取影响系数n=1.5,极限切削力F=120 N,以此作为单个锯齿的失效的标准。根据计算结果,不同△y时,极限切削力失效的临界值如表2所示。
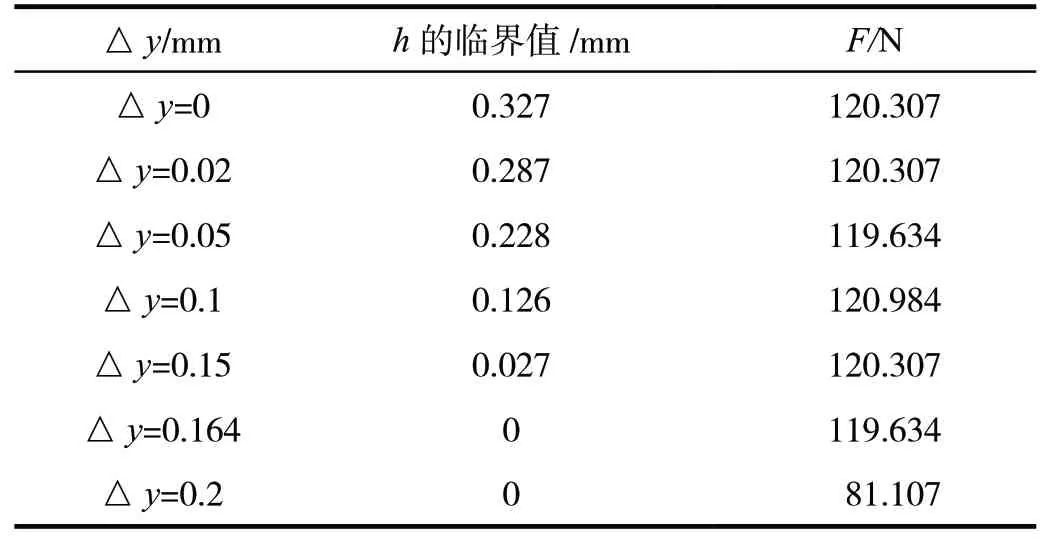
表2 不同△y时,h的临界值
由表2可知裂纹中心偏移量△y超过0.164 mm时,h的临界值为0,即△y超过此值,一旦存在裂纹,就无法满足切削要求。随着△y增大,h的临界值在减小,以△y为横坐标、h为纵坐标作图,得到h临界值与△y的关系图,如图4所示。
由图4可知,h的临界值与△y呈线性关系,即h取值在0~0.327 mm内,△y在0~0.164 mm内时,极限切削力F才满足要求。

图4 h-△y关系图
2.2 裂纹位置对单个锯齿切削力影响分析
为了更便于观察裂纹位置对单个锯齿切削力的影响。分别取h为0、0.05 mm、0.1 mm、0.2 mm,将△y由0开始取值,以0.01 μm为步长,分别计算极限力F,并绘制“F-△y”图像,如图5所示。

图5 F-△y图
由图5可知,观察任一曲线,当h一定时,极限切削力F随△y增大而减小,并呈现二次函数下降趋势。根据计算结果,不同h时,极限切削力失效的临界偏移量△y的临界值如表3所示。
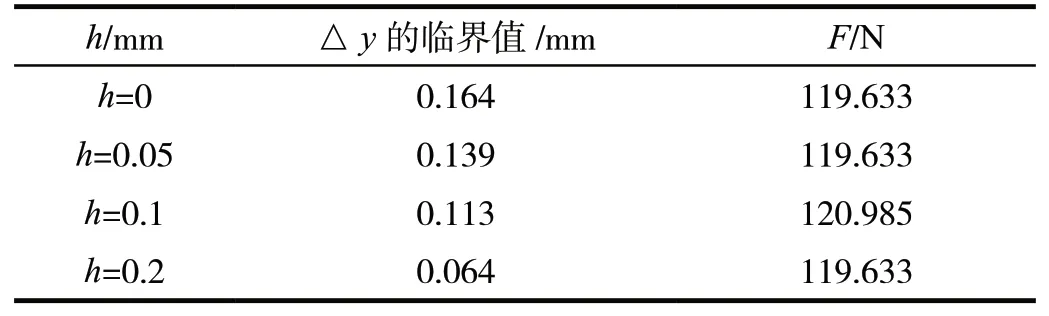
表3 不同h时,△y的临界值
根据表3,以h为横坐标、以△y为纵坐标作图,得到△y临界值与h的关系图,如图6所示。
由图6可知,△y的临界值与h呈线性关系,进一步验证了图4的分析。

图6 △y-h关系图
综上所述,单个锯齿的极限切削力F与裂纹大小h和裂纹相对位置△y均呈二次函数关系,并且是下降趋势。且h和△y这两个影响极限切削力的参数之间呈现线性关系。
3 结论
课题组提出了考虑焊接工艺缺陷的锯齿切削力数学模型,并通过公式推导,得到了“F-h”曲线以及“F-△y”曲线;从而揭示了当存在焊接裂纹时,锯齿的极限切削力与焊缝h和位置△y的关系。研究结果表明:极限切削力F与焊缝大小h和△y之间均呈二次函数下降关系;且以某双金属带锯条参数为例,分析得到△y大于0.164 mm或h大于0.327 mm时,极限切削力F将不满足切削要求;综上数据分析可知,裂纹大小h和相对位置△y均在一定程度上会影响极限切削力,因此,在双金属带锯条的制造中,应充分考虑和检测裂纹等焊接缺陷,以便提高切削性能并延长使用寿命。

