静压钢板桩贯入阻力试验与数值仿真

李宇航，高振宇，杨雪强，刘 攀

（1.广东工业大学 土木与交通工程学院,广东 广州 510006；2.广东首汇蓝天工程科技公司,广东 广州 510075）

近年来，随着静压桩机的推广和应用，许多学者对静压桩进行了数值模拟，分析了静压桩的沉桩过程与机理。在静压桩贯入数值分析方面，Sheng等[1]用有限元软件对桩体进行了数值模拟，得到的沉桩阻力与实测的数据较为吻合，但是模拟得到的桩端阻力与实测结果有差距。李镜培等[2]使用有限元方法，选用Drucker-Prager弹塑性土体模型，比较了有、无桩尖两种情形下土中应力场的不同，并分析了影响应力场变化的各种参数。鹿群等[3]在ANSYS平台上，应用位移贯入法对静力压桩连续贯入的全过程进行有限元模拟。Fan等[4]分析了不同参数对桩锥稳定性的影响，采用Arbitrary Lagrangian Eulerian(ALE)自适应网格技术，对砂土响应进行了数值模拟。Gennaro等[5]采用轴对称的有限元模型，解决了桩土界面的接触问题。寇海磊等[6]采用不同的本构模型，模拟了层状黏性土及砂土地基中静压桩的连续贯入过程，得出了贯入过程中沉桩阻力随深度变化的曲线。陈亚东等[7]利用ABAQUS软件对常规桩筏基础和复合桩基进行了三维弹塑性分析，验证了复合桩基理论的正确性。桑松魁等[8]采用位移贯入法和Mohr Coulomb准则，建立了静压桩位移贯入土体的有限元模型，实现了桩体的连续贯入。Ostnoff等[9]采用CEL方法，模拟了U型钢板桩和Z型钢板桩在贯入砂土过程中腹板和翼缘的变形特性。牛永昌[10]借助静压桩的沉桩阻力及承载力的现场试验数据，用ABAQUS有限元软件对静压桩的沉桩阻力、桩端阻力等进行了系统分析。张吉坤等[11]用ABAQUS软件建立了静压桩连续贯入土体的有限元模型，探讨了沉桩过程中桩周土体的应力与应变分布特征，得到了贯入阻力随深度变化的规律。郝友超[12]利用ABAQUS数值模拟软件，对沉桩过程中压桩力、桩端阻力以及桩侧摩阻力随沉桩深度的变化进行了分析，实现了模型桩在砂土内连续贯入的数值仿真。

本文采用ABAQUS有限元软件，对佛山市芦苞镇工程静压钢板桩的贯入过程进行了数值模拟，研究了钢板桩(U型)在贯入成层土的过程中贯入阻力随深度变化的规律，再将模拟结果与现场实测结果进行比较。

1 数值模拟

1.1 模拟方法

桩体在贯入土层过程中，土体会产生大变形。如果使用基于拉格朗日公式的经典有限元方法模拟钢板桩的贯入，将会导致网格的扭曲变形。为解决网格大变形问题，本文采用CEL方法进行模拟，把钢板桩离散为拉格朗日区域，在该区域中元素节点与材料相耦合；土体离散为欧拉区域，在该区域中材料可以在欧拉网格里自由流动，从而降低网格扭曲变形的风险。用CEL方法模拟桩体贯入土层的过程如图1所示[13]。

图1 用CEL法模拟桩体贯入土层过程的示意图Fig.1 Schematic diagram of CEL method for simulation of pile penetration into soil layer

当拉格朗日体(桩)进入土层时，会与欧拉体产生接触，欧拉区域中的材料产生流动，材料的位置通过单元的欧拉体积分数(Eulerian Volume Fraction,EVF)来描述。当材料完全充满单元时，该材料在当前所在单元的体积分数为“1”，否则为“0”。

欧拉时间积分通过Lagrange-plus-remap公式和中心差分算子来计算[14]。该过程首先经历传统的拉格朗日阶段，然后传递至欧拉阶段。在拉格朗日阶段，节点被临时固定在材料上，然后单元随材料一起变形；传递到欧拉阶段时，网格变形被抑制，发生有效变形的单元自动恢复原状，并相应地计算出相邻单元的材料流动[15]。

1.2 数值模型的建立

为模拟钢板桩单桩沉桩的过程，建立桩土三维模型。土体选用Mohr Coulomb本构模型，假定各层土体都为均质连续的弹塑性土体，桩为刚性体。由于桩土的变形及受力情况是对称的，为简化运算，本文建立1/2的桩土模型。土体为半径1 m、高12 m的圆柱体，桩为长9 m、厚10.5 mm的U型钢板桩，各取一半如图2所示。

图2 桩土模型尺寸草图Fig.2 Pile soil model dimension sketch

该工程场地位于广东省佛山市芦苞镇，场地地貌类型主要为剥蚀残丘及丘前冲积阶地地貌单位，地势总体为南高北低，东西向总体地形变化不大。根据地质勘察报告及实际地层情况，将土体划分为3个土层，各层土体材料参数根据地质勘察报告选取，具体参数如表1所示。钢板桩材料参数依据实际情况选取，详见表2。

表1 土层材料参数Table 1 Soil layer material parameters

表2 钢板桩材料参数Table 2 Material parameters of steel sheet pile

1.3 土体初始地应力平衡

由于土体存在自重应力，所以建立桩土模型时首先应进行土体的初始地应力平衡。本文在地应力平衡时采用step-1和initial两个分析步。在step-1分析步中选择“静力、通用”。在载荷模块initial分析步中定义边界条件BC1、BC2和BC3，分别限制土体的左、右、下面的法向位移，然后在模块load中给整个模型的U3方向设置重力系数−9.8 N/kg，最后提交作业进行分析得到ODB文件。检查竖向位移U3和竖向应力S33，若未取得较好的平衡效果，需切换至载荷模块，在编辑预定义场中导入上一步分析得到的ODB文件，直至取得较好的平衡效果。通过多次导入ODB文件，本模型得到了较好的地应力平衡效果，平衡后的竖向位移达到10−6～10−7数量级，满足地应力平衡后竖向位移的精度要求，位移云图如图3和图4所示。

图3 地应力平衡前竖向位移云图Fig.3 Vertical displacement cloud map before ground stress balance

图4 地应力平衡后竖向位移云图Fig.4 Vertical displacement cloud diagram after ground stress balance

本文采用显示动力学方法模拟沉桩过程，该方法在分析步中不能直接添加地应力，因此在建立欧拉体后，需在载荷模块的预定义场中导入上述模型得到的最后一次地应力平衡ODB文件，完成土体的初始地应力平衡。

1.4 桩土接触的设置及网格划分

钢板桩贯入土层的过程中，桩周土体随着钢板桩不断贯入发生变形，桩与土之间的相互作用是非线性的。在模拟桩土接触时采用基于罚函数的通用接触算法,在罚函数接触算法中其接触约束的严格性低于运动学算法[17]，更适合大变形问题。采用这种算法，可以更好地反映钢板桩在贯入土体时单元产生较大扭曲的情况。切向行为摩擦公式采用库伦摩擦(Coulomb Friction)，摩擦系数为0.1。

土体模型如图2所示，在土体顶部建立了高为0.5 m的无材料空层，这个空层既没有材料也没有强度，当土体表面隆起时，土体中的欧拉材料可以进入其中。模型中土体采用97 080个八结点线性欧拉六面体EC3D8R单元；钢板桩采用5 400个八结点线性六面体C3D8R单元。

2 钢板桩沉桩过程及结果分析

模型中土层上方有高为0.5 m的无材料空层，空层区域没有强度也没有密度，钢板桩置于土层表面。模型荷载施加方式采用位移法，在载荷模块对钢板桩施加9 m的位移，完成沉桩。

2.1 剪胀角对模拟结果的影响

土体发生塑性剪切时，剪胀角控制着塑性体积应变的大小。在有限元数值计算中，剪胀角的取值范围在0°和内摩擦角之间。目前，在模拟计算时大多数文献都采取剪胀角为0°或剪胀角和内摩擦角相等的做法。当剪胀角取为0°时没有考虑土体的体积膨胀，服从非相关联流动法则；当剪胀角与内摩擦角相等时服从相关联流动法则，土体会发生过度膨胀。两种极端做法显然都是不合理的，为此，本文探讨了不同的剪胀角对模拟结果的影响。

因粉细砂层在地表5.46 m以下，钢板桩下沉会导致较深位置处的粉细砂易处于剪缩状态，而ABAQUS有限元软件不允许取负的剪胀角，所以本文粉细砂层的剪胀角取为0°。

剪胀系数[18]η=ψi/φi=0∼1，ψi为不同土层的剪胀角，φi为不同土层的内摩擦角，在模拟过程中设定粉细砂层土体剪胀角为0°，另外2层土体的剪胀角变化一致，剪胀系数如表3所示。

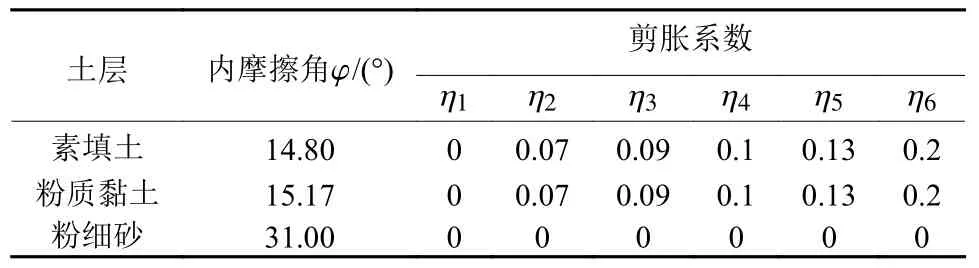
表3 土体剪胀角参数Table 3 Parameters of soil dilatancy angle

图5为不同剪胀系数下的等效塑性应变云图。从图5可以看出，随着剪胀系数的增大，塑性区的范围逐渐增大，剪胀系数在0～0.1范围内，塑性区增加不明显，剪胀系数在0.1～0.2范围内塑性区范围明显增大。图6为不同剪胀系数对应的最大沉桩阻力。从图6中可以看出，随着剪胀系数的增大，土体的抗剪切能力逐渐增大，从而导致桩体的贯入阻力增加。剪胀系数在0～0.09范围内，模拟的最大沉桩阻力增加幅度较小；剪胀系数在0.09～0.13范围内，模拟的最大沉桩阻力急剧增加；剪胀系数大于0.13时，模拟的最大沉桩阻力增加幅度放缓。其中，剪胀系数等于0.1时，模拟的最大沉桩阻力与实测的最大沉桩阻力最为接近。

图5 不同剪胀角塑性区分布云图Fig.5 Cloud diagram of distribution of plastic zone with different dilatancy angles

图6 剪胀系数与最大沉桩阻力关系图Fig.6 Relationship between dilatancy coefficient and maximum pile sinking resistance

2.2 桩周土体的应力分布

由于不同剪胀系数下的应力云图形状大致相同，本文不再详细列出，只选取剪胀系数为0.1时的应力云图进行分析，如图7所示。从图7中可以看出，钢板桩在沉桩过程中挤压周围的土体，土体向四周扩散，钢板桩端附近产生了应力泡，桩端周围出现应力集中现象，而且应力集中的区域随着贯入深度不断变化。从水平向应力云图可以看出，钢板桩两侧的压力泡并不是特别的对称，这是由于桩底受到挤压的土体在桩内侧聚集形成土塞，钢板桩内侧应力影响范围较大。

图7 沉桩完成后桩周土体应力分布Fig.7 Soil stress distribution around piles after sinking

2.3 数值模拟与现场实测数据对比分析

在ABAQUS中提交任务后，利用后处理技术，输出沉桩阻力，把输出的沉桩阻力数据导入到Excel中，随后利用模拟所得的沉桩阻力数据与静压钢板桩工程实际测得的压桩数据进行比较。同时绘制不同剪胀系数对应的沉桩阻力随深度变化的曲线图，如图8所示。

从图8可以看出，实测的沉桩阻力与ABAQUS数值模拟得到的结果有差异，但两者的变化趋势较为吻合，沉桩阻力随贯入深度的增加而增加，这是由于钢板桩在沉桩过程中，桩底部土体受到挤压扩散，在钢板桩U型槽内侧形成土塞，随着贯入深度的增加，土塞愈发明显，沉桩阻力持续增大。

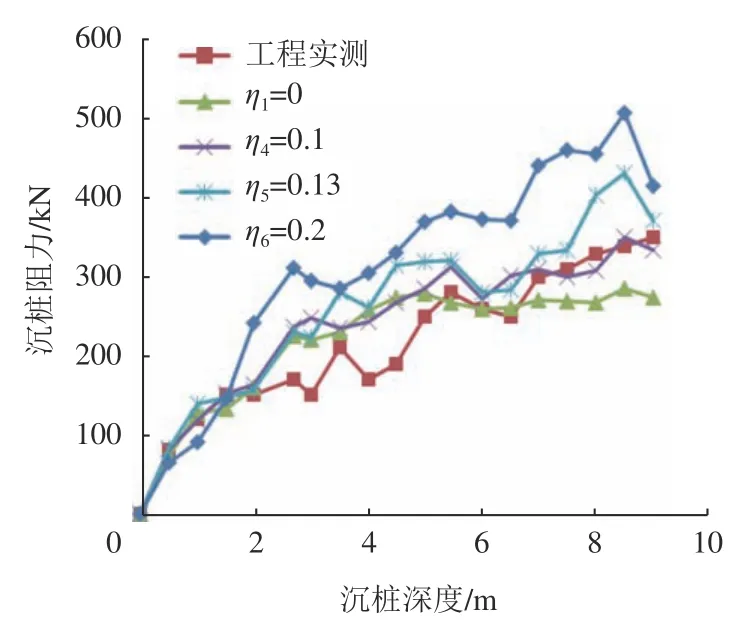
图8 沉桩阻力随深度的变化曲线Fig.8 Curve of resistance of sinking pile with depth

图8显示，在2.76 m处钢板桩贯入第二层土时，实测值与模拟值均缓慢增加，这是由于当桩贯穿不同土层时，贯入力需增大到一定值才能穿透土层，贯入后贯入力先减小后缓慢增大，因两者土层性质较为接近，所以贯穿土层时力的变化幅度较小。在深度为5.4 m 左右(第二层土与第三层土分界线)处可以看出，钢板桩贯入第三层土时，所需沉桩压力急剧增大，贯入之后贯入力减小后缓慢增大，这是由于第三层土质相对较硬，当桩从相对较软的土层贯入相对较硬土层时，需较大的贯入力，这与文献[6]所述一致。

对比钢板桩沉桩结束时最大沉桩阻力的模拟值与实际值，不考虑剪胀角的影响时，模拟的最大沉桩阻力为286 kN，工程实测的最大值为350 kN，模拟结果与实际值有较大差异。考虑剪胀角的影响时,模拟的最大沉桩阻力基本随着剪胀角的增大而增大，经过不断调整剪胀角的大小，得出剪胀系数为0.1时模拟的最大沉桩阻力值与实测值最为接近。剪胀系数为0.13和0.2时模拟的最大沉桩阻力分别为432 kN和509 kN，两者与工程实测值均有较大出入。

剪胀系数为0.1时的沉桩阻力值与实测值虽然较为接近，但两者仍存在偏差，偏差主要集中在粉质黏土层，即使粉质黏土剪胀角为0°，该土层的沉桩阻力预测值也仍大于实测值，分析原因可能在于：(1)工程实测值是通过静压桩机的油压表读数的，该读数只能读取整十的数值，并不精确；(2)勘察中粉质黏土的黏聚力与内摩擦角的设置值较大，与实际土层情况有一定差异。

3 结论

(1)利用ABAQUS有限元软件模拟了钢板桩贯入成层土的过程，得到了沉桩压力随深度变化的曲线，并与工程实测值进行了对比分析，两者曲线变化趋势基本吻合，验证了数值模拟沉桩过程的可行性，对静压钢板桩沉桩的研究具有一定的参考意义。

(2)钢板桩在沉桩过程中，桩底土体受到挤压在桩内侧聚集形成土塞，产生较大的沉桩阻力。在工程施工时，对于砂性土层可采取灌水的方法，降低桩土间的摩擦，从而便于沉桩。

(3)模拟时采用了单一的Mohr Coulomb本构模型，钢板桩贯入9 m时，不考虑剪胀角的影响，模拟的最大沉桩阻力为286 kN。考虑剪胀角的影响，当剪胀系数为0.1时，模拟值与实测值的最大沉桩阻力最为接近。由此可见，剪胀角对模拟结果有较大的影响，在数值模拟土体时不可忽视。

(4)模拟时虽然得到剪胀系数为0.1时的最大沉桩阻力与实测值最为接近，但桩体贯入粉质黏土层时，两者沉桩阻力随深度变化的曲线仍有偏差，可能是因为静压桩机油压表的读数不精确及勘察中粉质黏土的黏聚力与内摩擦角的设置值较大。