基于缓存的时变道路网最短路径查询算法

黄 阳 周 旭 杨志邦 余 婷 张 吉 曾源远 李肯立

1(湖南大学信息科学与工程学院 长沙 410082) 2(之江实验室 杭州 311100)

近年来，随着现代综合化交通运输体系结构的改变，无线通信网络安全的快速发展，具有定位功能、提供地图服务的设备在物联网中被广泛应用.利用基于位置服务来获取从指定源点到目标点的最短路径查询结果已经逐渐成为主流的查询方式.尤其是面临紧急情况出行时，人们往往选择旅行时间最短的路径作为行驶路线，但是现实世界道路网中街道旅行时间具有时变性，交通状况并不稳定，会面临道路临时修建、雷雨天气等突发事件，导致街道的旅行时间发生动态的改变.尽管已经存在许多求解最短路径的方法，但是能否高速有效地实现检索动态道路网中旅行时间不确定的最短路径仍面临如下问题：

1) 查询结果的时效性与查询请求响应速度的平衡问题.文献[4]提出无索引方法，在保证路径权重有效的情况下，通过服务器计算2点之间成本最小的路径，但在非大规模图上执行路径查询仍需花费几秒钟，其查询性能有待提高.为解决查询耗时长的问题，文献[5]提出预构建全局索引的算法，以加速最短路径查询.虽然引入全局索引的查询技术能够快速响应查询请求，但索引维护开销较大，将面临索引未完成更新，路况就可能发生了新的变化的情况，导致查询结果不适用路况而变得无效.

2) 查询响应速度与服务器工作负载的平衡问题.当道路网处于查询高峰期时，查询请求的峰值可达百万次，此时服务器将产生极高的工作负载、延迟查询的响应时间.虽然可以通过部署更多的服务器解决负载过高的问题，但成本昂贵，并非所有公司都可以承担.该挑战在可以保证查询结果有效性的无索引算法中尤为突出.为提高大规模路径的查询效率，可利用缓存中的数据来提升查询请求的响应能力，减少服务器工作负载.文献[7]通过引入缓存技术启发式地将动态图中收益值最大数据替换缓存中无效路径来提高缓存命中率，加速查询效率.然而该方法只适用于单路径更新的场景.文献[8]利用历史日志信息将查询频率高的数据预加载到缓存来提高缓存命中率.而复用历史日志信息中的高频路径来构建缓存，并不适用于时变道路网场景，主要是因为过往数据不具备时效性，不能应对动态变化的场景，导致缓存命中率降低，命中的路径也因数据失效而出现结果偏差，继而影响用户体验.

例如，在偏远地点

A

开设一场万人以上的大型演唱会，那么在演唱会当天会存在上万次前往地点

A

的路径查询请求

.

若是基于历史信息的缓存策略，偏远地区的数据不会预存入缓存，缓存则不会命中有关地点

A

的查询请求，从而只在代理服务器中执行查询

.

此时，若出现大量与地点

A

相关的查询，将导致服务器负荷骤增，系统整体的查询性能变差

.

若此时提供一种可以实时识别查询频率高的路径并用来替换缓存中的低效的路径，则可以有效地避免上述情况的发生

.

意味着在演唱会当天，缓存中的数据能够及时且有效地应答多条前往地点

A

的路径查询请求，以减少代理服务器的计算量

.

此外，当地点

A

的查询频率变低后，缓存中与

A

相关的数据则会自动被其他高频率数据置换.

通常采用15 min为一个时钟间隔来更新缓存数据，该方式得以有效应用，是因为一段时间内路况的变化非常小，短时间内可以维持命中路径的准确性.因此采用实时更新缓存数据的方式不仅可以提高缓存命中率，减少服务器的运行成本，还可以提高命中数据结果的有效性.

综上分析，在具有时变特征的道路网中，一个良好的基于缓存的最短路径查询算法是能够支持最短路径快速查询和提高缓存命中率的必要条件.因此，本文设计了一个尽可能最大化利用缓存的算法来支持最短路径查询.并在缓存存储策略中，将路径共享能力计算方法和差异多样性技术相结合，用于减小缓存中冗余数据的占用容量，提高缓存命中率.此外，缓存中的数据存储结构具有数据弱相关、结构紧凑的优点，不仅可以减少数据的存储空间，还可以实现动态数据的快速维护、加快路径的检索速度.

本文主要贡献有3个方面:

1) 提出的新缓存存储结构包含用于存储节点的邻接点索引、记录路径节点的位图索引以及记录路径基本信息的路径信息索引.该结构新颖之处在于其存储空间较小，索引间可独立地维护缓存中的数据;

2) 提出一种缓存存储策略，其不仅显著地减少了缓存中的冗余数据，还可以有效且实时地识别出存入缓存的最短路径，以提高缓存命中率.

3) 提出了基于缓存的时变道路网最短路径查询算法(cache-based time-varying shortest path query, CTSPQ).其巧妙地借助缓存存储结构的特性，提高了最短路径在缓存中的查询速度.

在真实的数据集上进行大量实验，验证了本文提出的策略以及查询方法的有效性.

1 相关工作

1.1 最短路径查询

近年来，最短路径查询问题被广泛应用在各行各业，其变体问题被广泛用来研究，如查找从给定源点到目标点最短路径的单源点对(single pair shortest path, SPSP)问题、查找给定顶点到图中每个顶点最短路径的单源点(single source shortest paths, SSSP)问题以及查询图中所有顶点最短路径的全对(all-pairs shortest path, APSP)问题.但是在道路网中检索最短路径的花费时间仍旧高，如常用的Dijkstra算法的时间复杂度为

O

(

m

+

n

log

n

).

为解决大规模网络上最短路径查询耗时长的问题，文献[5,12-17]提出了支持快速检索最短时间/油耗/距离路径问题的索引结构，缩小了最短路径查询理论与实践之间的差距.文献[14]设计的HoD(highways-on-disk)索引结构通过采用较小的I/O消耗成本来回答单原点距离(single source distance, SSD)和SSSP等查询问题，但HoD仅适用于数据变换频率低的情况.文献[15]通过使用关系数据库管理系统解决了SSSP查询慢的问题，但是当网络中的数据或者结构发生变化时，该方法将耗较长的时间重新计算节点之间的关系.

文献[16]给出了维护索引结构时间复杂度的理论上下界，最优下界与网络中顶点数量呈线性关系，但在节点数量非常庞大的网络中才能表现出线性优势。文献[17]利用随机化技术提出了一个有效预测路径距离的方法.是通过以空间换时间的方法来构建索引，虽然可以通过部署大量服务器提高查询速度，但运行成本高、可扩展性较差.

1.2 缓存管理

缓存具有快速交换数据的能力，文献[18-25]利用缓存技术减少大规模最短路径查询时间.即预先构建一个缓存区，若缓存中的数据能够直接应答查询请求并返回结果，则无需采用代理服务器计算路径，从而加快系统整体的响应速度.故利用缓存加速查询的关键点在于查询请求在缓存中命中率.

现有提升缓存命中率的策略主要有3种：动态缓存策略、静态缓存策略及混合缓存策略.静态策略将根据历史日志中查询频繁的路径对缓存进行更新，该策略的数据无法应对突发事件，不适用于本文.动态策略包括最近最少使用(least recently used, LRU)和最不经常使用(least frequently used, LFU)等，LRU策略是将新路径置换缓存中最近最久未使用的路径的策略，LFU策略则是将当前时间使用次数最多路径置换缓存中使用次数最少的路径，以此来提高缓存命中率.文献[19]设计了最短旅行时间的路径缓存(shortest travel-time path cache, TPC)算法，用于计算时变道路网中旅行时间最短的路径，但路径能否加入缓存依赖于缓存已有节点.文献[20]提出的最短路径缓存(shortest-path-cache, SPC)方法，虽然能回答查询频繁高的路径，但面对突发状况时的查询将不具备稳定性.混合缓存策略将静态策略和动态策略相结合来更新缓存.

除此之外，文献[22]利用寄存器设计了通用的框架来生成时序关键路径，减少了相同查询请求的计算次数，但其存储空间较小.文献[23]引入的Cache-Oblivious模型为多级内存系统设计算法提供了理论基础.该模式是专门为标准的两级I/O模型设计的算法，但需要小心地调优它们所运行的系统的参数.文献[6]提出了批量处理最短路径的算法，首先将查询请求生成云状查询集，再利用缓存统一查询以减少查询次数.文献[8]不仅考虑了日志路径的查询频率，还通过路径的覆盖范围来衡量最短路径的影响力，将高影响力的路径存储入缓存，进而提高其命中率.文献[24]设计了路径缓存规划系统，将缓存中部分匹配的查询请求结果的路径作为返回用户端路径的子路径段，以此减少服务器对整条路径的计算量.文献[25]不再关注网络节点之间的组织情况，而是通过边来构造路径缓存，首先定位查询请求点在缓存中的候选边，由边之间连接得到最短路径.虽然上述缓存技术可以加速最短路径查询、平衡索引维护的时间和路径查询速度的关系，但仅有少部分文献涉及时变道路网中最短路径查询的缓存策略，因此在高度动态网络中，利用缓存设计高速、有效应答路径查询方法变得十分重要.

1.3 基于差异多样性的路径规划

提高缓存命中率的常规方法是将高频率路径加入缓存，但高频路径往往存在大量重复路径段.为减少冗余数据存入缓存，本文采用差异多样性技术来避免缓存存储大量相似的路径.现在有关差异性的研究多集中在数据新颖度，或者多目标空间Skyline查询的问题上，但不适用于本文的场景.虽然也有学者研究路径多样性问题，但并不能完全移植到当前问题，因为在道路网中求解具有差异多样性的路径是一个NPC问题，除此之外，在不同场景下处理数据方式不一，时间复杂度也不相同.

文献[29-30]基于阈值剪枝策略来测量路径的差异多样性，以此减少路径查询以及比较路径之间相似性的次数.其中，文献[29]结合阈值约束条件，返回

K

条不仅可以兼顾查询结果总得分还能兼顾查询结果多样性的数据，既除掉了结果集中相似的数据又保证了结果的质量.但这种用精确查找的方式来获取最优结果的耗时较长，与本文提高用户响应速度的目标背离.文献[30]通过结合相似度阈值精心地设计了算法的下界，以计算从查询源点到目标点的前Top-

K

条不相似的最短路径，有效地减少了搜索空间并显著提高了效率.不同于文献[29-30]，本文在引入差异多样性策略的同时，采用贪心思想实现最大化存入缓存的

K

条最短路径的收益，进而减少服务器的计算量

.

其中存入缓存的

K

条路径来自不同查询结果，是互不相关的路径集合，这些路径既存在差异性，又存在共同节点，便于路径紧密联系

.

此处，缓存中的路径数量

K

并非固定数值.

2 定 义

本节重点介绍基于缓存的时变道路网最短路径查询的相关理论.表1描述了基本符号.

Table 1 Summary of Notation

2.1 基本定义

定义1.

时变道路网模型

.

时变道路网

G

=(

V

,

E

,

W

,

T

)，其中

V

和

E

分别表示

G

的节点集和边集，节点

v

∈

V

，边

e

=(

v

,

v

)∈

E

，函数

W

:

E

×

T

→

RV

表示边集

E

在时刻

T

的权重映射函数，其中边

e

=(

v

,

v

)的时间权重为

w

(

v

,

v

)

.

定义2.

最短路径

.

给定道路网

G

=(

V

,

E

,

W

,

T

)，

G

上从

v

到

v

的所有路径中，具有最短旅行时间的路径

P

，被称为最短路径

P

，其中节点

v

,

v

∈

V.

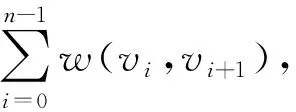
定义3.

查询请求

.

在道路网

G

=(

V

,

E

,

W

,

T

)上，由用户终端发出查询请求

Q

，用于查询从

v

∈

V

到

v

∈

V

的最短路径

P

.

其中

v

称为

Q

的查询源点，

v

称为

Q

的查询目标点

.

定义4.

缓存空间容量

.

给定缓存

C

，

C

中所有最短路径的集合为

ψ.

其中，

C

的空间容量为|

C

|，

C

中数据的占用空间为|

ψ

|≤|

C

|

.

定义5.

完全命中、部分命中及未命中

.

给定缓存

C

和查询请求

Q

,完全命中表示

C

的最短路径集

ψ

中至少存在一条包含节点

v

,

v

的最短路径，完全命中的路径集可形式化为ц(

P

)={

P

,|(

v

∈

P

,)∧(

v

∈

P

,)∧ (

v

≠

v

),

P

,∈

ψ

}；部分命中表示

ψ

中至少存在一条包含节点

v

或

v

的最短路径，部分命中

v

的路径集可形式化为ц(

v

)={

P

,|(

v

∈

P

,)∧(

v

∉

P

,),

P

,∈

ψ

}；否则称为未命中，即

ψ

中不存在包含节点

v

或

v

的最短路径

P

，未命中可形式化为∀

P

∈

ψ

,(

v

∉

P

)∧(

v

∉

P

)∧(

v

≠

v

),其中，完全命中意味着

ψ

中至少存在一条最短路径的子路径作为

Q

的结果

.

由文献[20]提出的最优子路径性质可知，最短路径的子路径也是最短路径，故完全命中获得的路径可以保证命中结果的准确性

.

定义6.

连接路径

.

给定最短路径

P

,和

P

′,′，节点

v

,

v

∈

P

,，

v

,

v

∈

P

′,′，存在子路径〈

v

→…→

v

〉⊆

P

,和〈

v

→…→

v

〉⊆

P

′,′,⊆表示路径间的包含关系

.

通过

v

连接2条子路径组成一条从

v

到

v

再到

v

的新路径，该路径称为连接路径

JPath

(

v

,

v

)=〈

v

→…→

v

→…→

v

〉

.

其中连接路径

JPath

(

v

,

v

)可近似为最短路径

P

，用于应答查询请求

Q

，减少服务器的计算量

.

2.2 问题定义

本节给出CTSPQ问题的形式化定义.

定义7.

CTSPQ

(

G

,

v

,

v

,

C

,

T

,

T

)

.

给定节点

v

,

v

∈

G

，

C

为时刻

T

的缓存，

T

为每条最短路径在

C

中滞留的最长时间

.

记

ψ

为时刻

T

之前存入

C

的

n

条最短路径集合，

Ω

为时刻

T

待存入

C

的

m

条最短路径集合，

Sh

为

Pi

∈(

ψ

∪

Ω

)的共享能力，

t

为

Pi

存入

C

的时刻

.

0-1变量

x

表示

Pi

是否存储于

C

中，

x

=1表示

Pi

存于

C

中，

x

=0表示

Pi

未存

C

中，并记

X

=(

x

1,

x

2,…,

x

(+))

.

CTSPQ的目标是最大化缓存

C

中最短路径集

ψ

的收益

B

(

ψ

,

Ω

,

T

,

T

)，并以在线的形式在

C

中快速规划出一条从

v

到

v

的最优最短路径

P

，使得服务器的计算量最小

.

其中，

B

(

ψ

,

Ω

,

T

,

T

)满足：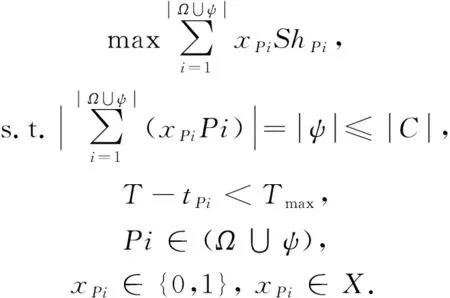

(1)

缓存技术之所以能提高路径查询速度是因为其可以降低服务器对数据库的读操作

.

因此，能否较好地解决CTSPQ问题取决于

C

中

ψ

的收益，即缓存收益越大，命中越高

.

此外，加入缓存

C

的路径数量有限，若

C

中的数据无法应答从

v

到

v

的查询请求，则可从服务器中查询并获取最短路径

P

.

由式(1)可知，求解缓存最大收益问题的时间复杂度为

O

(

n

|

C

|)，是一个伪多项式问题

.

其计算成本较高，因此本文将采用贪心思想计算缓存中数据的最大收益，以减少构建缓存的计算时间

.

3 基于缓存的时变最短路径缓存查询算法

本节首先介绍基于缓存的时变道路网最短路径查询算法CTSPQ的总体框架.如图1所示，框架包含3个模块：查询请求检测模块、最短路径评估模块和缓存管理模块.首先从用户终端发出具有真实地理坐标源点

v

(

lat

,

lng

)和目标点

v

(

lat

,

lng

)的查询请求

Q

(步骤①)；通过查询请求模块将

v

(

lat

,

lng

),

v

(

lat

,

lng

)映射为节点

v

,

v

∈

G

，以转化为

G

上的查询请求，继而从缓存

C

中获取

Q

完全命中或部分命中的路径作为候选路径集(步骤②～④)；然后，在最短路径评估模块判断候选路径集中是否存在有效应答

Q

的路径，若是则将一条近似最优的路径返回用户终端，否则从代理服务器检索

Q

的最短路径，并返回到用户终端(步骤⑤～⑧)；此外，缓存管理模块中的缓存结构用于存储数据，缓存存储策略决定从服务器获取的实时最短路径是否能存入

C

(步骤⑨～⑩)

.

Fig. 1 CTSPQ schematic diagram图1 CTSPQ框架示意图

3.1 缓存管理模块

构建索引是加速最短路径查询的主要技术之一，在数据的检索和存储中起着重要作用.因此本文在本模块中设计了便于更新缓存数据的索引结构以及提高缓存命中率的路径缓存存储策略，以快速响应时变环境下的查询请求，减少服务器的工作负载.

如图1所示，无论执行哪个模块，只要执行操作皆离不开缓存中的数据.即一旦触发其他模块，缓存管理模块也随之触发.

3.1.1 缓存存储结构

图2展示了一个简单缓存最短路径的例子.根据图2(a)的子图得到了图2(b)的5条最短路径，并按照路径节点的旅行顺序将路径存入缓存列表，如路径

P

=〈

v

→

v

→

v

→

v

〉存放节点的顺序为

v

,

v

,

v

,

v

.

当存在查询请求

Q

时，首先判断缓存列表中的路径是否存在从由

v

到

v

的子路径，若是则直接应答

Q

.

如查询请求

Q

可由图2中的

P

应答

.

虽然此存储方式可应答查询请求，但会导致缓存出现大量的冗余数据，如

v

存储了3次，

v

存储了4次，甚至出现了冗余路径，如

P

是

P

的子路径

.

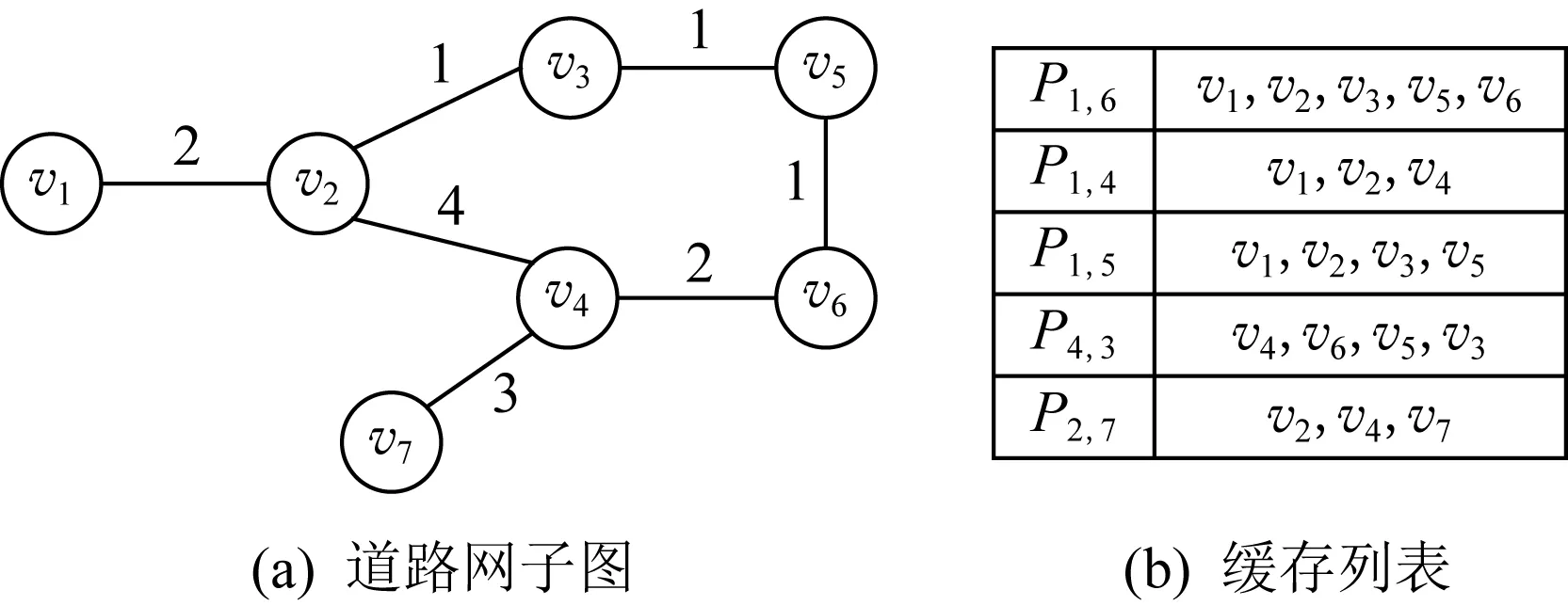
Fig. 2 An example of simple cache storage图2 简单缓存实例图

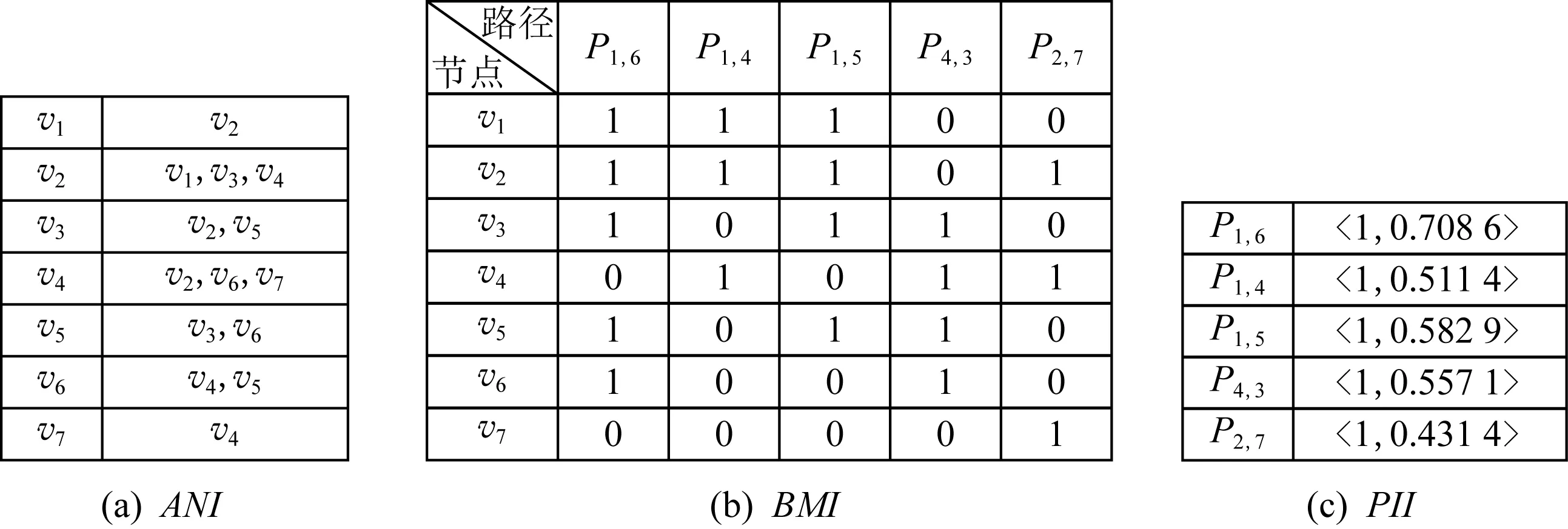
Fig. 3 An example of the AMPS storage path图3 AMPS存储路径示意图

因此，为减少数据的存储空间，本文设计了一个数据弱相关、结构紧密的缓存存储结构.该结构由存储节点的邻接点索引(adjacency node index,

ANI

)、存储路径的位图索引(bit map index,

BMI

)以及记录路径基本信息的路径信息索引(path information index,

PII

)等3部分组成，并简称为AMPS.图3展示了以AMPS形式存储图2中5条最短路径的例子.1) 邻接点索引

ANI.

ANI

记录了缓存

C

中每条路径节点的邻接点关系，记为邻接点对〈

v

,

v

〉，并为返回一条有序的最短路径做准备

.

其中，每个邻接点对在

ANI

中最多存储一次，表示

C

中至少存在一条从

v

到

v

(或从

v

到

v

)的路径

.ANI

引用了文献[8]的模型，它无需存储

G

上所有邻接点对关系，减少了冗余数据存入

C.

以图3(a)为例，

v

的邻接点有

v

，

v

和

v

，存在路径

P

,

P

经过

v

到达

v

；

P

,

P

经过

v

到达

v

.

虽无路径经过

v

到达

v

，但存在经过

v

到达

v

的路径

P

,

P

和

P

，故

ANI

记录了邻接点对〈

v

,

v

〉的关系

.

2) 位图索引

BMI.

BMI

以位图形式记录了最短路径

P.

如图3(b)所示，存在于路径上的节点用“1”标注，否则标注为“0”，其中路径

P

=〈

v

→

v

→

v

〉上的节点

v

,

v

,

v

在

BMI

中被“1”标记

.

因为位图可以执行二进制操作，因此

BMI

可以快速识别查询请求的候选路径，并快速判断

C

中数据所涉及的节点

.

以图3(b)为例快速识别

Q

和

Q

的候选路径

.

令操作

BMI

(

v

)表示求解节点

v

所在的路径集合，请求

Q

通过执行

BMI

(

v

)∩

BMI

(

v

)={

P

,

P

}得到完全命中的候选路径集；而

Q

执行

BMI

(

v

)∩

BMI

(

v

)=∅，无完全命中的候选路径集，但可以通过部分命中操作获取与源点

v

和目标点

v

相关的2个部分命中候选路径集

BMI

(

v

)={

P

,

P

},

BMI

(

v

)={

P

}，根据候选路径集执行连接操作获得应答

Q

的连接路径，即通过

v

连接候选路径

P

和

P

获得答查询请求的候选连接路径

JPath

(

v

,

v

)=〈

v

→

v

→

v

→

v

〉

.

3) 路径信息索引

PII.

PII

记录了

ψ

中每条路径

P

的基本信息〈

t

，

Sh

〉，用于更新缓存

C

中的数据，以保证从缓存中得到有效的查询结果

.

其中

t

表示

P

加入

C

的时刻、

Sh

表示

P

的共享能力(见定义8)

.

利用

t

计算

P

在

C

中滞留的时长，当时长超过

T

时，从

C

中移除

P

；

Sh

用于判断

P

是否被新路径置换，因为路径共享能力是反映路径受欢迎程度和重要性的指标，是计算缓存收益的主要影响因素

.

定义8.

路径共享能力

.

给定道路网

G

=(

V

,

E

,

W

,

T

)上的一条最短路径

P

=〈

v

→

v

→…→

v

〉，

P

的路径共享能力记做

Sh

.

归一化的

Sh

可形式化为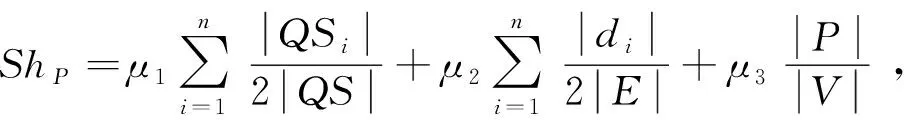

(2)

其中,0≤

μ

，

μ

，

μ

≤1，

μ

+

μ

+

μ

=1；

QS

为当前

G

中所有查询请求的集合，|

QS

|为

QS

中请求的数量；|

QS

|为节点

v

∈

P

在

QS

的源点集和目标点集中出现的次数；|

d

|为节点

v

∈

V

的度数；|

E

|表示边

E

的数量；|

V

|为节点集

V

中节点的数量；

P

的节点数量为|

P

|=

n.

以图2举例说明路径共享能力的计算方法，记图2(a)为道路网子图

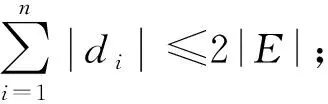
G

′，令图2(b)中最短路径的查询请求为查询请求集

QS

,

μ

=0

.

4,

μ

=0

.

2,

μ

=0

.

4；故|

QS

|=5,|

E

|=7,|

V

|=7

.

若求解

P

=〈

v

→

v

→

v

→

v

→

v

→

v

〉共享能力，可知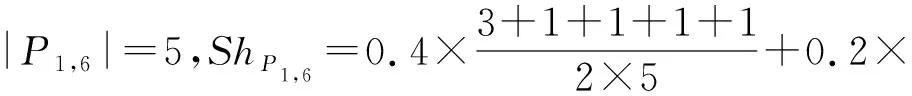

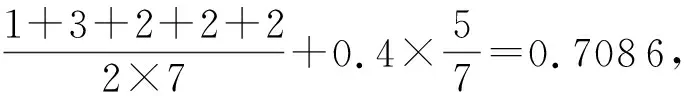
类似方法可得其余4条最短路径的共享能力见图3(c)

.

算法1展示了在时刻

T

将最短路径

P

加入缓存

C

的伪代码

.

假设

P

的共享能力为

Sh

，首先获取

C

中AMPS的数据(行①)；接着依次遍历

P

上的节点

v

及其邻接点

v

+1∈

P

，并将2点添加至

BMI

,

ANI

中，其中，若

ANI

中已存在邻接点对〈

v

,

v

+1〉的信息，则无需对索引

ANI

进行操作(行②～④)

.

最后将

P

的信息〈

T

，

Sh

〉存入

PII

，并返回

C

(行⑤～⑥)

.

算法1.

插入算法

Insert

(

P

,

C

,

T

,

Sh

)

.

输入：新路径

P

、缓存

C

、当前时间

T

、共享能力

Sh

；输出：缓存

C.

①

ANI

,

BMI

,

PII

←

get

(

C

);

/

*从缓存

C

中获取索引信息*

/

② for each node

v

in

P

③

add

(

ANI

,

BMI

,

v

,

v

,

P

);

/

*分别在

ANI

,

BMI

中添加邻接点对〈

v

,

v

+1〉及路径

v

∈

P

信息*

/

④ end for

⑤

addPII

(

PII

,

T

,

Sh

);

/

*将

P

的信息加入

PII

*

/

⑥ return

C.

以图3为例，令

T

=1,|

ψ

|=0，此时向

C

中添加共享能力为0

.

511 4的最短路径

P

=〈

v

→

v

→

v

〉

.

首先从

v

开始，在

ANI

中加入

v

的邻接点

v

，

v

的邻接点

v

，在

BMI

中用“1”标注

v

∈

P

；然后在

ANI

中加入

v

的邻接点

v

，

v

的邻接点

v

，在

BMI

中用“1”标注

v

∈

P

；循环上述步骤，直至用“1”标注

v

∈

P

；最后在

PII

中添加

P

的信息〈1,0

.

511 4〉

.

算法2.

删除算法

Delete

(

P

,

C

,

T

)

.

输入：删除路径

P

、缓存

C

、当前时间

T

；输出：缓存

C.

①

Z

←空栈,

D

←空集合;②

ANI

,

BMI

,

PII

←

get

(

C

);

/

*从缓存

C

中获取索引信息*

/

③

v

′←

random

(

P

);

/

*随机获取

P

上的一个节点*

/

④

Z.push

(

P

,

v

′,

D

);

/

*将节点

v

′入栈

Z

*

/

⑤ while 栈

Z

中存在元素时⑥

v

←

Z.pop

();

/

*出栈

Z

中的元素放入

v

*

/

⑦ if节点

v

′和

v

当且仅当存在于路径

P

⑧

delete

(

ANI

,

v

,

v

′ );

/

*在

ANI

中删除邻接点对〈

v

,

v

′ 〉的信息*

/

⑨ end if

⑩

D.add

(

v

)；

/

*记录已删除的节点*

/

中的邻接点入栈

Z

*

/

/

*删除

PII

,

BMI

中

P

*

/

3.1.2 缓存收益模型

求解缓存最大收益问题是NPC问题，本文首先采用简单的Baseline策略构建缓存数据.Baseline策略结合了贪心思想，将路径共享能力近似为路径存入缓存的收益，在保证在较高命中率的前提下，减少存储过程的计算量.Baseline策略首先按照待加入缓存的最短路径共享能力以从大到小的顺序依次加入缓存

C

，直到

C

中无多余空间存入新路径，因此Baseline的时间复杂度为

O

(

n

lg

n

)

.

以图4说明采用Baseline策略构建路径缓存

C

的方法

.

在道路网子图

G

′上，首先为方便计算

C

中数据的占用空间|

ψ

|，举例时仅考虑

PII

及

ANI

的占用空间

.

令一个节点的占用空间为1，一条

PII

信息占用空间为2，

T

=6，初始化|

ψ

|=0，|

C

|=16

.

在

T

=1时，待加入

C

的3条最短路径的共享能力的大小依次是

Sh

>

Sh

>

Sh

.

故首先确定

P

加入

C

需要在

ANI

中增加10个节点(5个邻接点对)，故将

P

加入

C

时|

ψ

|=10+2<|

C

|；接着

P

是

P

的子路径，只需增加

PII

信息，加入

C

时|

ψ

|=12+2<|

C

|；最后判断

P

加入

C

还需在

ANI

中新增邻接点对〈

v

,

v

〉，占用4个空间，而|

ψ

|+4=18>|

C

|，故

P

不被加入

C.

此时缓存中的共享能力总和为0

.

861 9+0

.

695 2=1

.

557 1，并且可以应答路网上

v

～

v

之间的查询请求

.

虽然采用Baseline策略可以减少构建缓存的计算量，但是无法避免子路径等冗余数据存入缓存，如

P

是

P

的子路径

.

然而道路网中访问频率高的路径，其子路径也往往具有较高的访问频率，这些子路径极易存入缓存

.

因此在第3

.

1

.

3节改进了Baseline策略

.

Fig. 4 Example diagram of TSPC strategy图4 TSPC策略实例图

3.1.3 改进存储策略

本节为优化Baseline策略提出了时变最短路径缓存(time-varying shortest path cache, TSPC)策略.该策略在Baseline的基础上结合了差异多样性技术，在保证缓存路径有效的前提下，尽可能使得缓存中的任意2条路径不相似，以减少缓存中的冗余数据，达到提高缓存命中率的效果.

衡量数据相似度常用的方法为Jaccard相似系数，但Jaccard适用于衡量路径重合度而差异性.故本文改进相似度度量方法来判断缓存路径的相似性.

定义9.

相似度度量

.

给定最短路径

P

和

P

以及相似度约束值

τ

，

P

和

P

相似度为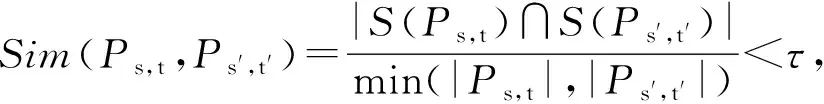

(3)

其中,|

S

(

P

)∩

S

(

P

)|表示

P

和

P

具有一样节点的数目；min(|

P

|,|

P

|)表示

P

和

P

之中拥有较少节点数量的数值；

τ

的取值范围为[0,1]

.

与Jaccard略为不同，本文相似度度量方法选择min(|

P

|,|

P

|)作为分母，它可以清楚地感知较多节点数目的路径能够作为较少节点数目路经的共享路径

.

其中，

τ

值的大小决定缓存中路径间最高相似度，

τ

值越大冗余数据越多

.

TSPC策略的最坏时间复杂度为

O

(

kn

+

n

lg

n

)，其中

k

表示|

ψ

|=

k

，

n

表示在时刻

T

待加入缓存的最短路径数量，

O

(

n

lg

n

)表示排序的时间复杂度，

O

(

kn

)表示构建

k

条互不相似最短路径的最大开销

.

而最优时间复杂度是

O

(

n

lg

n

)，即共享能力最大的前

k

条最短路径两两不相似

.

以图4为例说明TSPC策略构建缓存

C

的方法

.

为方便与Baseline策略进行比对，TSPC的初始条件与Baseline一致，除此之外，令

τ

=0

.

7

.

当

T

=1时，首先对待加入

C

的3条最短路径按照其共享能力排序，即

Sh

>

Sh

>

Sh

.

由TSPC策略可知，先将

P

加入缓存

C

，此时|

ψ

|=12<|

C

|；接着判断

P

与

C

中路径集

ψ

的相似度，由

Sim

(

P

，

P

)=1>

τ

可知，

C

拒绝

P

的加入；接着判断

P

与

C

中

ψ

的相似度，即

Sim

(

P

,

P

)=2

/

3<

τ

，此时将

P

加入

C

需在

ANI

中新增邻接点对〈

v

,

v

〉，占用空间为|

ψ

|+4=16≤|

C

|，故将

P

加入

C.

虽然缓存的共享能力总和为0

.

861 9+0

.

523 8=1

.

385 7<1

.

557 1(Baseline策略1

.

557 1)，但缓存

C

中的数据不仅可以应答Baseline策略可应答的查询，还可以通过构建连接路径应答与

v

有关的查询请求，提高了缓存的命中率

.

此外，当

T

=7时，待加入

C

的2条最短路径的共享能力为

Sh

>

Sh

.

首先由

T

-

T

=1可知，在1时之前加入

C

的路径已逾时，故清空缓存

C

，|

C

|=0

.

接着将

P

加入

C

，空间容量|

ψ

|=10<|

C

|，然后判断

P

与

C

中

ψ

的相似度，

Sim

(

P

,

P

)=2

/

3<

τ

满足约束条件，还需在

ANI

中增加邻接点对〈

v

,

v

〉、

PII

中增加基本信息，|

ψ

|+4=14<|

C

|，故可将

P

加入

C.

算法3.

TSPC更新缓存算法

Update

(

C

,

P

,

T

,

T

,

τ

)

.

输入：缓存

C

、最短路径

P

、当前时间

T

、最大滞留时间

T

、相似度阈值

τ

；输出：缓存

C.

①

Z

←空优先队列,

D

←空优先队列;②

Sh

←根据式(2)计算路径

P

的共享能力;③ for each

Pi

in

C

④ if

T

-

t

≥

T

⑤

Delete

(

Pi

,

C

,

T

,

Sh

);

/

*删除路径

Pi

*

/

⑥ else if

Sim

(

Pi

,

P

)>

τ

且

Sh

<

Sh

⑦

Z.push

(

Pi

);

/

*将路径

Pi

入队

Z

*

/

⑧ else if

Sh

<

Sh

⑨

D.add

(

Pi

);

/

*将路径

Pi

入队

D

*

/

⑩ end if

/

*删除缓存

C

中与

Z

有关的路径*

/

/

*将

P

加入缓存

C

*

/

/

*将缓存

C

中与

Z

相关的路径删除*

/

/

*出队

D

中的路径并删除缓存

C

与其相关的数据，直至缓存容量满足|

C

|≥|

ψ

+

P

|*

/

3.2 查询请求检测模块

本模块用于识别缓存中可应答查询请求的候选路径集.在位置坐标评估时需执行节点映射操作，是因为真实地理空间中的坐标是连续不断的，而现有的存储设备无法将所有坐标点存入存储设备，所以首先将连续坐标点映射成离散点.

映射可以将查询节点变得规范，不仅可以快速确定查询请求能否在缓存中命中路径，还可以识别同一批次中查询结果相同的查询请求，通过共享一个结果，减少查询次数.

为快速定位地理空间坐标点在

G

上的位置，本文采用KD-Tree索引映射二者之间的关系.与基于网格均匀划分区域空间的方式不同，KD-Tree将节点多的区域分割更加细致，节点少的区域分割更加粗糙.以此来提高映射的效率，为批量处理提供条件.在获取应答

Q

的候选路径集时，只需通过当前缓存中BMI的信息查询与源点

v

和目标点

v

相关的路径，即获得部分命中的候选路径集ц(

v

)和ц(

v

)，以及完全命中的候选路径集合ц(

P

)

.

3.3 最短路径评估模块

本模块用于评估从查询请求检测模块得到的候选路径集能否应答查询请求.本模块可以通过执行直接查询操作(direct query operation, DQO)，选择一条最优路径应答查询请求，或者通过执行连接查询操作(join query operation, JQO)获取一条连接路径用于应答查询请求.若2种操作皆无法获取应答查询请求的路径，则只能通过代理服务器获取最短路径.

直接查询操作DQO表示从ц(

P

)中选择一条距离当前时间最近的最短路径应答

Q

.

DQO可形式化为

DQO

(ц(

P

),

T

,

T

)，满足：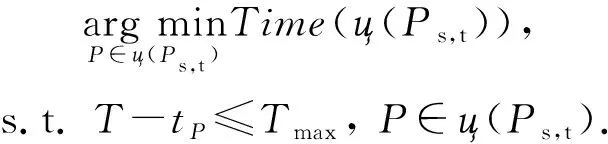

(4)

连接查询操作JQO表示从ц(

v

)及ц(

v

)中各任选一条路径

P

∈ц(

v

),

P

′∈ц(

v

)来组成连接路径

JPath

(

v

,

v

)应答

Q

.

其中，

JPath

(

v

,

v

)需要满足时间约束

T

以及欧氏距离约束

EDR

(

v

,

v

,

v

)

.

JQO形式化为

JQO

(

v

,

v

,

θ

,

T

,

T

)，满足：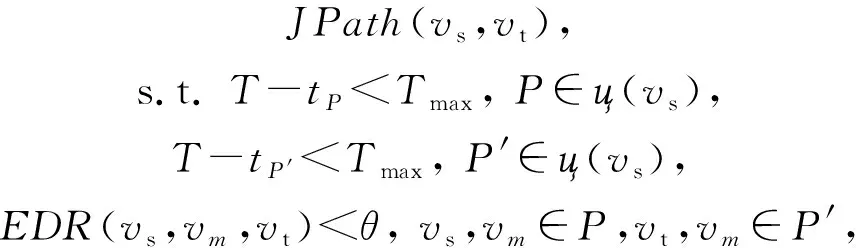

(5)

其中，JQO引入距离约束阈值

θ

，是因为连接路径

JPath

(

v

,

v

)的连接点

v

可能偏离最短路径

P

，并出现在很远的位置，此时连接路径的旅行时间将变得不可靠

.

为避免连接路径的偏离，故设置欧氏距离比来控制

v

的偏离程度，即：

(6)

表示从

v

到

v

和

v

到

v

的欧氏距离之和与

v

到

v

的欧氏距离比小于

θ.θ

的大小影响连接路径的旅行时间，

θ

越小连接路径的长度越趋近于最短路径，但当

θ

=1时并不一定是最短路径

.

算法4.

查询算法

CTSPQ

(

C

,

Q

,

G

,

θ

,

T

)

.

输入：缓存

C

、查询请求

Q

、道路网

G

、欧氏距离比

θ

、最大滞留时间

T

；输出：最短路径

P.

① ц(

v

),ц(

v

)←空栈;

P

←空集;

sign

←false;

PII

,

ANI

,

BMI

←从缓存

C

中

获取数据信息;

②

v

,

v

←

KD

-

tree

(

Q

,

G

);

/

*查询请求映射*

/

③ ц(

v

)←

BMI

(

v

)；

/

*获取

v

所在的路径*

/

④ ц(

v

)←

BMI

(

v

)；

/

*获取

v

所在的路径*

/

⑤ if ц(

v

)∩ц(

v

)的路径集合不为空⑥

P

←

DQO

(

v

,

v

,

T

,

T

);

/

*见式(4)*

/

⑦ return

P

；

/

*返回路径

P

*

/

⑧ else

⑨

P

←

JQO

(

v

,

v

,ц(

v

),ц(

v

),

θ

)；

/

*见式(5)*

/

⑩ if 存在连接路径

P

/

*从服务器获取路径*

/

以图3为例，在时刻

T

发出查询请求

Q

，首先将

Q

的源点和目标点映射到道路网子图

G

′上的节点

v

和

v

，然后在索引

BMI

中执行部分命中操作

BMI

(

v

)={

P

,

P

,

P

},

BMI

(

v

)={

P

,

P

,

P

}获取候选路径集ц(

v

),ц(

v

)和ц(

P

)，在ц(

P

)中存在路径

P

满足|

t

4,3-

T

|<

T

，即满足DQO约束，故可以直接向用户端返回路径

P

.

路径

P

的旅行次序可以结合索引

BMI

和

ANI

中的数据获得

.

而获取旅行次序的过程与删除过程相似，继续以

P

为例说明如何确定路径走向

.

令

D

记录已检索邻接点的节点，

Z

记录已访问但未检索邻接点的节点，第1步，通过

random

(

P

)函数随机获取节点

v

为

P

检索起点，

Z

={

v

}；第2步，根据

ANI

检索既在

P

上又是

v

邻接点的节点{

v

,

v

}，此时

D

={

v

},

Z

={

v

,

v

}

.

第3步，

Z

出栈

v

，在

P

上

v

的邻接点集为{

v

},

v

∈

D

已被访问，且无其他邻接点，故可确定

P

的一段子路径为〈

v

→

v

〉，此时

D

={

v

,

v

}、

Z

={

v

}

.

同理，

Z

出栈

v

，找到

v

邻接点

v

,

v

，而

v

∈

D

已被访问，得到

P

的另一段子路径〈

v

→

v

→

v

〉，此时

D

={

v

,

v

,

v

}，

Z

={

v

}

.Z

出栈

v

，其在

P

上的邻接点为{

v

}，而

v

∈

D

，

Z

=∅，已遍历上的

P

所有节点，故通过检索起点

v

连接2条子路径段可确定

P

的旅行方向为〈

v

→

v

→

v

→

v

〉

.

4 实验分析

本节通过在真实数据集上进行大量实验，验证了所提算法的有效性及可扩展性.

4.1 实验设置

本文实验环境见表2，采用的编程语言为Java.此外在相同的环境下，本文分别对SPC,EPC,Baseline,TSPC策略方法进行了对比测试.

Table 2 Experiment Environment

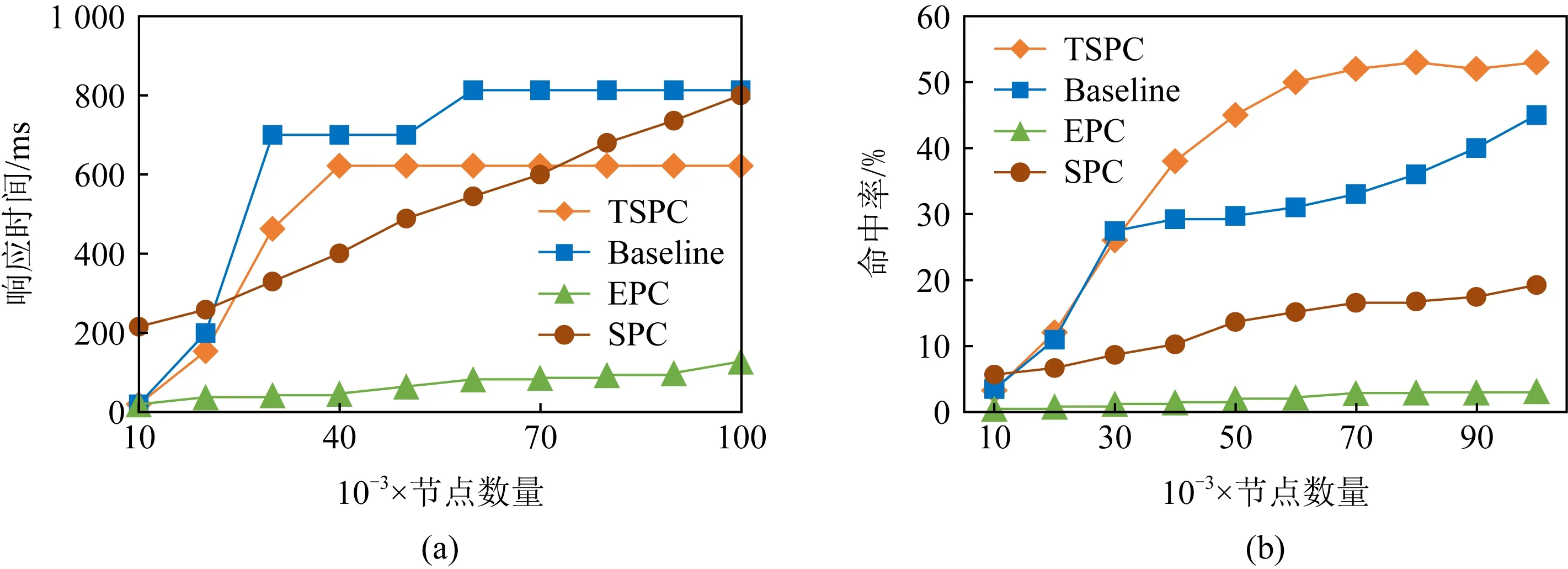
Fig. 6 Effect of cache size图6 缓存大小的影响

4.2 数据集

本文使用的实验数据集来自文献[25]，利用加利福尼亚州道路网上的真实数据集进行实验.该网络具有真实的兴趣点，包含了21 693条边、21 048个节点和104 770个兴趣点.我们从兴趣点中随机选择2点作为测试的源点和目标点，用于生成时空路径进行实验，此外，测试部分的数据除了来自文献[25]之外，还有来自必应地图的实时查询数据.在实验过程中利用必应地图的API作为提供准确的最短旅行时间的服务器.在测试之前我们随机获取某一时刻的查询来预热缓存.

本文所涉及的实验若无特殊说明则代表缓存最多可容纳的节点数为50 000(每个节点占4 B)，缓存中所有数据的总容量不超过1 MB，同一时刻下的查询请求数量设为10 000，构建缓存的候选路径数量设为10 000，相似度阈值设为0.7，距离约束设为1.05.

T

=15，缓存中路径滞留时间最大为15 min.

4.3 实验结果

4.3.1 映射

将地理坐标点映射到道路网

G

的过程中，本文采用了KD-Tree算法.KD-Tree划分的层级越多，映射结果越准确，为了更准确地识别数据，本文对道路网进行了精确的分割识别，在保证结果正确的前提下，可快速识别基于位置服务的点在

G

中的位置.图5描绘了Gird,KD-Tree,linear等方法在不同大小数据集下运行的时间.采用KD-Tree方法的映射速度明显优于Gird和linear方法.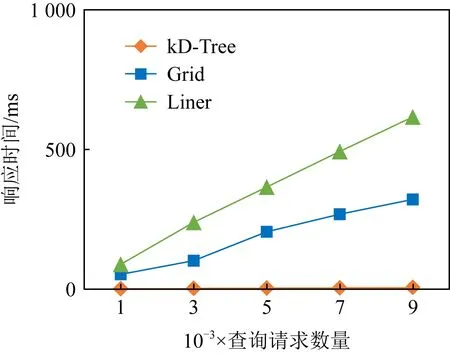

Fig. 5 Response time of different mapping methods图5 不同映射方法的响应时间

4.3.2 缓存大小

缓存容量的大小关乎整个系统的性能.缓存容量越小，命中率越低，但当缓存容量过大时，虽然命中率会明显提高，但会降低查询速度.

图6展示了不同缓存大小下SPC,EPC,Baseline,TSPC等算法的查询响应时间以及命中率，其中查询响应时间由映射过程时间以及在缓存中获取路径的时间组成.在图6(a)中，当缓存|

C

|>30 000时， 虽然EPC策略在缓存中的总耗时为TSPC,Baseline策略的10%～20%，但EPC在缓存中的命中率是TSPC和Baseline命中率的4%左右.综合分析，本文策略的整体效率较优.

在图6(b)中，随着缓存容量的增加，TSPC的命中率逐渐赶超Baseline的命中率.是因为受相似度的约束，TSPC缓存的节点种类比Baseline的多，可通过连接操作得到应答查询请求的路径.正因相似度约束，TSPC缓存的数据量并不会因为缓存容量的无限扩大而增加，缓存中的数据量会维持在一个范围内.

4.3.3 参数

θ

分析由三角形三边关系可知，在连接操作中引入欧氏距离比阈值

θ

，意味着连接路径的长度不会被无线延伸，可避免偏差较大的候选路径.图7显示了在不同

θ

下缓存的命中率及路径查询结果的准确度，

θ

的取值范围为[1.00，1.10].由图7(a)可知随着

θ

约束力度的放宽，以连接路径的形式应答查询请求的数量增多，命中率有较大的提升，但结果会出现较大的偏差.而在允许有10%的偏差下，TSPC和Baseline策略的命中率提升为90%以上，故在误差允许的范围内使用TSPC和Baseline可提高服务器的整体运行效率.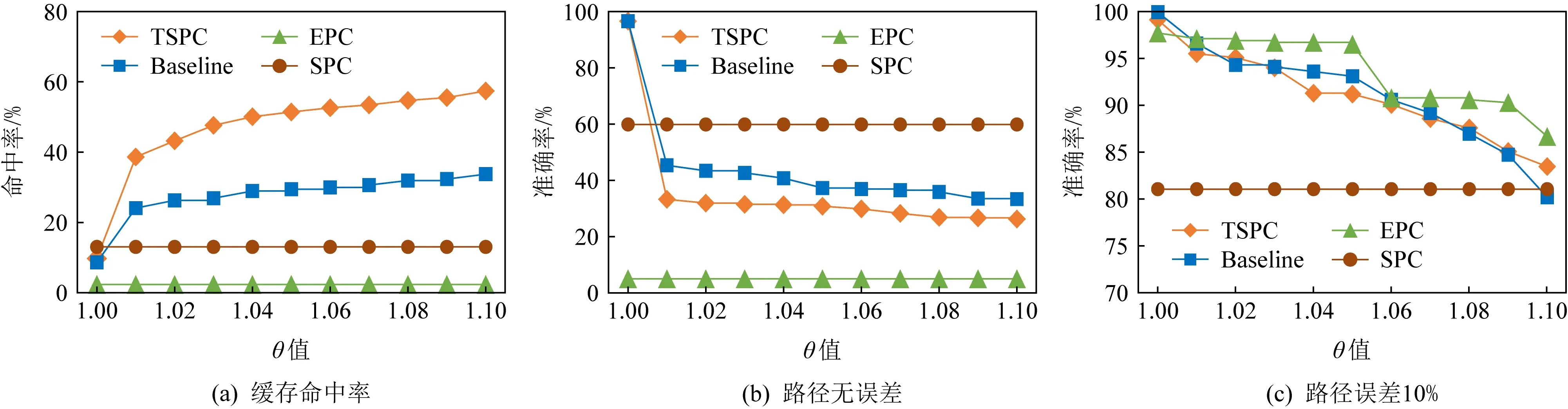

Fig. 7 Effect of θ图7 θ值的影响

Fig. 8 Effect of τ图8 τ值的影响

4.3.4 参数

τ

分析图8显示了不同相似度阈值

τ

下的命中率以及准确率，

τ

值大小影响缓存中路径的多样性

.

当

τ

=0时，表示缓存中的数据集不存在相同节点，也就意味着当执行查询操作时，缓存路径只能进行完全命中操作，此时准确率达到最高；当

τ

=1时，缓存中的存储的路径不再受到相似度的约束，而是仅受到缓存容量的限制，即为Baseline操作.如图8(a)所示，当

τ

∈[0.5,0.7]时，TSPC的缓存命中率远比未采用相似度约束的算法高，故相似度约束可明显改善小容量缓存的命中率.图8(b)～(c)显示了不同

τ

值下命中结果的准确率，虽然TSPC和Baseline策略在无误差情况下的准确率低于SPC的准确率，但是在

τ

=0.7时其命中率近似于SPC命中率的3倍，此外在容许存在10%误差的情况下，准确率达到90%以上.

5 总 结

针对时变道路网中在线查询最短路径效率慢的问题，本文利用缓存减少服务器的工作负载，首先为降低数据占用缓存空间，设计了一个缓存存储结构；其次，为实时地构建路径缓存提出了基于贪心策略和相似度约束的缓存存储策略，提高了缓存的命中率；最后根据存储结构中的索引特性，设计了一个利用缓存高效应答最短路径查询的算法.最终通过大量实验结果表明了本文所提的算法具有有效性和高效性.

作者贡献声明

：黄阳负责实验及论文的起草；周旭、杨志邦提出算法优化方案，为共同通信作者；余婷、张吉负责索引设计及文字润色；曾源远、李肯立负责实验方案及论文整体架构设计.