基于空间占有度的主导并置模式挖掘
方 圆 王丽珍 王晓璇 杨培忠
1(云南大学数学与统计学院 昆明 650500) 2(云南大学西南天文研究所 昆明 650500) 3(云南大学信息学院 昆明 650500)
空间并置模式(spatial co-location patterns, SCPs)代表一组不同类型的空间特征的组合,该组特征的实例在空间中频繁地共存.作为空间数据挖掘及空间关联规则挖掘领域的一个重要分支,空间并置模式挖掘(以下简称为SCPs挖掘)旨在发掘隐藏在空间复杂分布中的有趣知识,揭示空间特征之间的相关性,在生态学研究、公共卫生服务、基于位置的模式推荐、城市规划、决策支持等领域有着广泛的应用.
经典的SCPs挖掘过程首先收集位于同一邻域(实例间满足两两邻近关系)且属于同一特征组的实例组(并置实例),而后通过参与度-参与率度量提取频繁的空间并置模式.图1(a)显示了一个简单的分布数据集,其中6个空间特征A
,B
,C
,D
,E
和F
的实例分别用不同形状的顶点表示,实例之间的边代表2个实例之间有邻近关系.图1(b)列出了图1(a)数据集中模式{A
,B
,C
}的并置实例,以及模式的特征参与率(participation ratio,PR
)和参与度(participation index,PI
).假设频繁性阈值设置为0.3,则{A
,B
,C
}是一个频繁的SCP.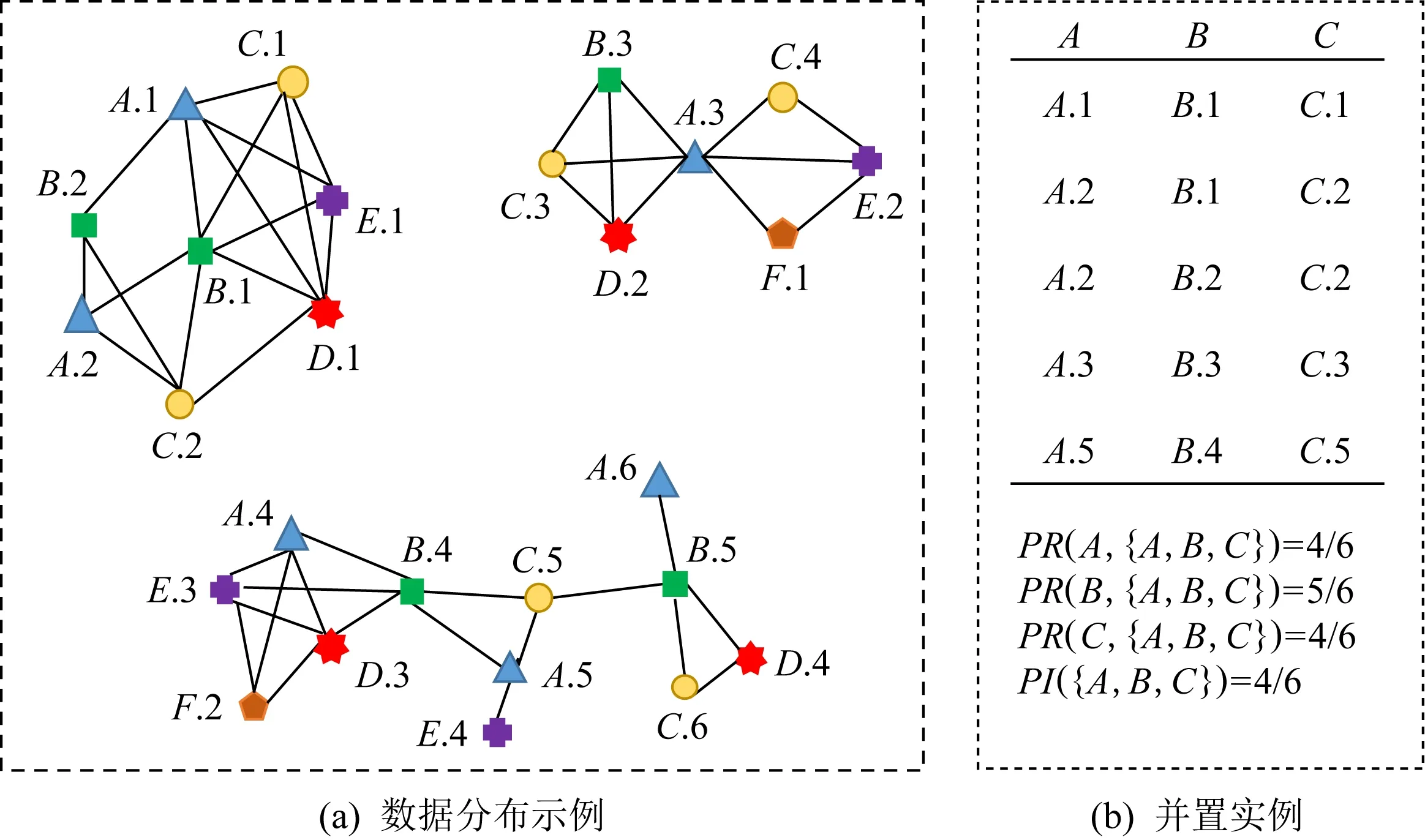
Fig. 1 An explanatory example图1 一个说明性示例
在某些空间并置模式的应用场景中,只考虑模式的频繁性,将参与度高的模式推荐给用户已不能满足用户的需求.例如,在城市公共基础设施规划中,频繁的空间并置模式代表了一组公共设施类型在城市区域分布中的普遍性.然而,这项应用更关心在模式代表的并置实例具有普遍性的基础上,尽量提供全面的公共基础设施,为居民的城市生活提供便利.因此,为了保证合理规划,规划者希望得到既具有普遍性又能较为全面地反映城市居民需求的一组公共基础设施类型,用以指导新城区的规划建设.在这项应用中,推荐给用户的模式需要结合并置模式的频繁性和完整性2方面的信息,才能更好地为用户提供决策支持.
经典的SCPs挖掘方法采用的参与度-参与率度量很好地体现了空间并置模式代表的一组空间特征共存的强度.然而,高阶SCPs的参与度往往比它的低阶子模式的参与度要低.因此,在要求模式的高参与度时,往往损失了模式代表的地理空间中特征信息的完整度.为了提高并置模式的可用性,我们引入了频繁项集挖掘中“占有度”的概念,来衡量空间并置模式的完整性,并结合空间占有度和参与度,提出了挖掘主导空间并置模式(dominant spatial co-location patterns, DSCPs)挖掘.与一般的SCPs模式只考虑模式的频繁性相比,DSCPs同时考虑了模式的频繁性和完整度,是一类可用性更高、信息更全面的高质量并置模式.
本文的主要贡献包括3个方面:
1) 提出了一种等价关系,称为实例间的连通关系,对并置模式的实例进行划分.基于该划分定义了空间占有率和空间占有度的概念,作为衡量并置模式完整性的指标;
2) 通过结合参与度和占有度指标,形式化定义了主导并置模式挖掘问题,并提供占有度和参与度之间的权重参数,让用户根据不同的偏好获得期望的挖掘结果.然后开发了一种称为DSCPMA算法(主导空间并置模式挖掘算法)来解决DSCPs挖掘问题;
3) 在DSCPMA算法的基础上探索了空间占有度度量的上限.此外,设计了一种新的数据结构,称为并置邻域表来存储实例,提出了一系列剪枝策略改进DSCPMA算法效率.
通过在具有不同数据密度和数据规模的几个合成数据集上改变参数设置的实验,测试了不同参数和所提出的剪枝策略对算法的影响.在不同数据集上的实验结果表明我们提出的DSCPMA算法可以有效地挖掘主导并置模式.
1 相关工作
并置模式挖掘在空间数据挖掘领域有着重要的作用.基于占有度度量的频繁项集挖掘也都有着广泛的应用和重要的研究意义.接下来,我们概述已有的部分空间并置挖掘方法及其在不同条件下的应用.
空间并置模式表示不同类型的空间特征子集的频繁共现.由于空间的连续性和复杂性,空间并置模式挖掘中缺乏事务数据库中频繁项集挖掘的事务概念.因此,Huang等人提出使用用户指定的邻域代替事务项来指定空间项集,并且还定义了一个频繁性度量,该度量具有理想的反单调性,即参与度(率),以衡量空间特征集的实例的共现频率.同时,开发了一种称为Join-base算法的类Apriori算法来发现所有频繁的并置模式.之后,鉴于join-base算法进行了大量的instance-join查询操作,为降低其在密集数据集上的计算开销,提出了一系列方法来提高基于连接的算法的效率.同时,随着并置模式挖掘的广泛应用,其应用场景变得愈加多样和复杂,为进一步提高并置模式挖掘的可用性,研究者从数据驱动和领域驱动2个方面对现有的模式挖掘方法进行改进及拓展.数据驱动方法侧重于在不同数据类型上挖掘并置模式,例如针对不确定数据、模糊对象、扩展对象、时空数据等不同数据类型的并置模式挖掘以及并置模式的压缩表示.并置模式压缩表示包括使用极大并置模式挖掘方法的有损压缩方法和使用闭的并置模式的无损压缩方法.同时,一些针对特定挖掘目的或领域知识约束的并置模式挖掘被相继提出,用以满足各种领域应用的需求.例如挖掘高效用并置模式、含主导特征的并置模式、区域并置模式、动态并置模式、具有特定关系的并置模式等.
作为一个有趣的新度量,“占有率”的概念由Tang等人提出,旨在捕获挖掘频繁项集模式的完整性,用于衡量模式(项集)在其支持事务中占据的比例.文献[38]将占有率度量扩展到序列数据,以挖掘高质量的序列模式.文献[39]将占有率概念引入到高效用模式挖掘中,提出了一种称为效用占有率的度量来衡量模式在支持事务中的贡献.Shen等人根据用户在频繁度、效用和占有率方面的偏好来挖掘高效用占有模式.由于每个项在实际应用中可能具有不同的重要性,因此Zhang等人将不同事务项的权重纳入占有率,挖掘具有频繁性和权重占有率的高质量模式.与使用模式的绝对大小作为约束的传统最大模式相比,占有率度量模式与其支持事务的相对大小,可以被视为一种更灵活的度量方法,并成功应用于许多需要挖掘结果的完整性信息的实际应用中,例如网页区域推荐、网络打印任务推荐、旅行路线推荐、商品匹配推荐等.
主导空间并置模式挖掘的任务看起来类似于基于占有率的项集挖掘问题,但实际上由于空间数据集中缺乏独立的事务概念,二者在挖掘方法上并不相同:1)空间数据占有率(度)度量与频繁项集挖掘工作的占有率度量定义不同.频繁项集挖掘工作中的传统占有率度量基于事物概念,事务数据库中的各项事务彼此独立.然而,空间特征的实例天然嵌入在连续空间中,并且彼此共享各种空间关系(例如邻居关系).因此,我们为空间并置模式挖掘开发了一种新的空间占有率(度)度量.2)挖掘目标不同.传统的基于占有率的事物数据挖掘旨在寻找频繁并占据其大部分支持事物的模式.然而,DSCPs挖掘旨在找到一组代表空间邻域中实例的大部分实例分布且特征之间具有强烈关联的并置模式.3)挖掘DSCPs的技术不同于基于占有率的事务数据模式挖掘的技术.DSCPs挖掘框架基于空间实例之间的邻近关系,而不是基于事务数据中独立的事务项,因此需要基于空间数据的特性,为DSCPs挖掘开发新的算法和新的数据结构.此外,空间占用率(度)度量不满足单调或反单调特性,因此需要探索新的剪枝策略来提高DSCPs挖掘的效率.
2 主导空间并置模式
2.1 基础概念
本节给出并置模式挖掘的一些基本概念和定义.由于符号较多,为了便于读者阅读,表1显示了本文对符号及其含义的统一描述.

Table 1 List of Notations
在空间数据库中,每个空间对象都被看作一个空间实例,且属于一个特定的事物类型(特征).
给定一个空间特征的集合F
={f
,f
…,f
}和一个空间实例集合S
=S
∪S
∪…∪S
(S
(1≤i
≤n
)是特征f
的实例集合),一个空间并置模式c
={f
,f
…,f
}是空间特征集F
的子集,c
⊆F
,模式中包含的特征个数k
称为并置模式的阶.
包括所有c
的特征且在给定的邻近关系R
下形成团的k
个实例组成的集合称为c
的并置实例,所有并置实例的集合称为c
的表实例,记为T
(c
).
如图1(a)所示,{A.
1,B.
1,C.
1}是{A
,B
,C
}的一个并置实例,{A
,B
,C
}的表实例如图1(b)所示.
值得一提的是,单个特征可以看作是阶数为1的频繁并置模式,其表实例是该特征的所有实例的集合.

min
_prev
,如果PI
(c
)≥min
_prev
,则c
是一个频繁的空间并置模式,一般来说,频繁的空间并置模式往往简称为空间并置模式(spatial co-location patterns, SCPs)或并置模式.
如图1(b)所示,PI
({A
,B
,C
})=4/
6,假设min
_prev
=0.
3,则{A
,B
,C
}是一个频繁共置模式.
引理1.
参与率(度)的反单调性.参与率和参与度随着模式阶数的增加而单调递减.2.2 相关定义
定义1.
实例的邻域.
给定一个空间特征的集合F
={f
,f
…,f
}及空间实例集S
,o
为特征f
(f
∈F
)的实例,则实例o
的邻域定义为IN
(o
)={o
∈S
|(o
=o
)∨((f
≠f
)∧R
(o
,o
))},(1)
其中,o
为特征f
(f
∈F
)的实例,R
为空间邻近关系.
定义2.
并置实例的邻域.
给定一个k
阶的空间并置模式c
={f
,f
…,f
},对于c
的任一并置实例l
={o
,o
,…,o
},并置实例l
的邻域定义为
(2)
相应地,c
的表实例邻域定义为c
所有并置实例邻域的集合:TN
(c
)={RN
(l
),RN
(l
),…,RN
(l
)}.
对于图1(b)所示的空间并置模式{A
,B
,C
}的表实例,其表实例邻域如表2所示.
图2(a)中的实线代表实例之间的邻近关系R
,圆圈内区域展示了{A
,B
,C
}的并置邻域,可以看到,模式的并置实例在空间上相互重叠.
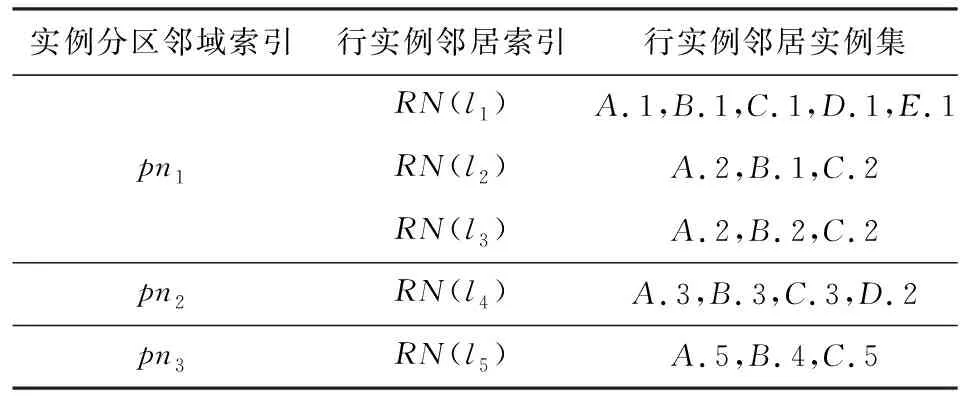
Table 2 Table Instance Neighborhoods of {A,B,C}

Fig. 2 Sample distribution data sets of {A,B,C}图2 {A,B,C}的数据分布样例
定义3.
连通关系及连通邻域.
给定一个空间实例集S
,对于任意2个空间实例o
和o
(o
,o
∈S
),在邻近关系R
下,若存在至少一条o
连通到o
的路径,那么o
和o
满足连通关系,记为CR
(o
,o
).
形式化定义如下:CR
(o
,o
))⟺{R
(o
,o
1),R
(o
1,o
2),…,R
(o
,o
)},(3)
其中,o
1,o
2,…,o
∈S.
若一组空间实例的子集O
={o
,o
,…,o
}(O
⊆S
)中的所有实例满足两两连通关系,则O
称为一个连通邻域.
定理1.
连通关系是一个空间实例集S
上的等价关系.
证明.
1) 自反性.
对于任意实例o
(o
∈S
),容易证明CR
(o
,o
).
2) 对称性.
对于任意2个空间实例o
和o
(o
,o
∈S
),容易证明CR
(o
,o
)⟺CR
(o
,o
).
3) 传递性.
对于任意3个空间实例o
,o
,o
(o
,o
,o
∈S
),若满足CR
(o
,o
)和CR
(o
,o
),则:CR
(o
,o
)⟺{R
(o
,o
1),R
(o
1,o
2),…,R
(o
,o
)},CR
(o
,o
)⟺{R
(o
,o
1),R
(o
1,o
2),…,R
(o
,o
)},那么,
{R
(o
,o
1),…,R
(o
,o
),R
(o
,o
1),…,R
(o
,o
)}⟺CR
(o
,o
).
连通关系满足自反性、对称性和传递性,是空间实例集S
上的等价关系.
证毕.
引理2.
给定一个k
阶的空间并置模式c
={f
,f
…,f
}和表实例T
(c
)={l
,l
,…,l
},对于T
(c
)的任一并置实例l
={o
,o
,…,o
}(l
∈T
(c
)),l
中的所有实例都属于连通关系下的一个等价类.
证明.
设2个空间实例o
和o
(o
,o
∈l
)满足R
(o
,o
),根据定理1,R
(o
,o
)⟺CR
(o
,o
),因此l
中的所有实例都属于连通关系下的同一等价类.
证毕.
引理3.
给定一个k
阶的空间并置模式c
={f
,f
…,f
}和表实例T
(c
)={l
,l
,…,l
},对于T
(c
)的并置实例l
,l
(l
,l
∈T
(c
)),若l
∩l
≠∅,则l
∪l
中的所有实例都属于连通关系下的一个等价类.
证明.
假设l
∩l
={o
},根据定理1中连通关系的传递性,任何l
和l
中的实例都通过与o
满足连通关系而相互满足连通关系,因此,l
∪l
中的所有实例都属于连通关系下的一个等价类.
证毕.
定义4.
并置实例的划分.
给定一个k
阶的空间并置模式c
={f
,f
…,f
},表实例T
(c
)={l
,l
,…,l
}在连通关系上的划分表示为并置实例等价类的集合:TP
(c
)={tp
,tp
,…,tp
},其中,tp
={l
,l
,…,l
}(tp
∈TP
(c
))代表T
(c
)的一个并置实例等价类,tp
∩tp
=∅,1≤i
<j
≤m.
相应地,任一并置实例等价类tp
(tp
∈TP
(c
))的实例集合ip
={l
∪l
∪,…,∪l
}称为并置模式c
的一个实例分区,则c
的实例分区集合定义为CIP
(c
)={ip
,ip
,…,ip
}.c
的实例分区满足3个条件:1)c
的任一分区中的所有实例都相互满足连通关系.
2) 属于c
的不同分区的2个实例o
和o
,不满足连通关系.
3)T
(c
)的任何实例都必须属于且仅属于c
的一个分区.
请注意,TP
(c
)是并置实例等价类的集合,其等价类中的元素是并置实例,而CIP
(c
)是实例等价类的集合,其等价类中的元素是实例.
定义5.
实例分区邻域.
给定一个k
阶的空间并置模式c
={f
,f
,…,f
},表实例在连通关系上的等价类集合TP
(c
)={tp
,tp
,…,tp
},及并置模式c
的实例分区CIP
(c
)={ip
,ip
,…,ip
},则对于任一并置实例等价类tp
(tp
∈TP
(c
)),其对应的实例分区ip
(ip
∈CIP
(c
))的邻域定义为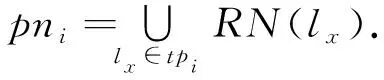
(4)
同样地,并置模式c
的实例分区邻域定义为c
的实例分区的邻域集合:PN
(c
)={pn
,pn
,…,pn
}.
例如:并置模式{A
,B
,C
}的实例邻域及分区邻域如表2所示,模式{A
,B
,C
}的表实例划分为TP
({A
,B
,C
})={{l
,l
,l
},{l
},{l
}},{A
,B
,C
}的实例分区邻域的集合为PN
({A
,B
,C
})={pn
,pn
,pn
},pn
=RN
(l
)∪RN
(l
)∪RN
(l
)={A.
1,A.
2,B.
1,B.
2,C.
1,D.
1,E.
1},pn
={A.
3,B.
3,C.
3,D.
2},pn
={A.
5,B.
4,C.
5}.
如图2(b)所示,实例之间的实线代表模式{A
,B
,C
}的实例之间的连通关系,圆圈内区域展示了{A
,B
,C
}模式的实例分区邻域,可以看到,实例的连通关系划分解决了并置模式的并置实例及其邻域的重叠问题.
在此基础上,我们给出了空间占有率及占有度的定义.
定义6.
空间占有率及空间占有度.
给定一个k
阶并置模式c
,c
的实例分区集合CIP
(c
)={ip
,ip
,…,ip
}及实例分区的邻域集合PN
(c
)={pn
,pn
,…,pn
},则任一实例分区ip
(ip
∈CIP
(c
))的空间占有率定义为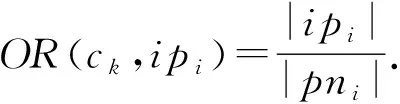
(5)
空间占有度定义为并置模式c
所有实例分区的空间占有率的最小值,即:
(6)
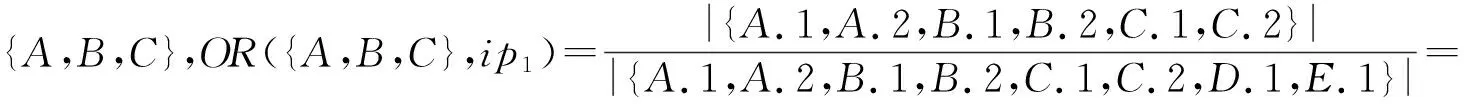
定义7.
模式质量.
给定一个k
阶并置模式c
,一个用户指定的权重参数ω
,则并置模式c
的质量定义为Quality
(c
)=ωPI
(c
)+(1-ω
)OI
(c
).
(7)
例如:假设权重参数ω
=0.
4,则并置模式{A
,B
,C
}的质量值为Quality
({A
,B
,C
})=0.
4×0.
67+0.
6×0.
75=0.
718.
2.3 主导空间并置模式挖掘问题
定义8.
主导空间并置模式.
给定一个空间特征集F
,空间实例集合S
,邻近关系R
,模式频繁性阈值min
_prev
(0≤min
_prev
≤1),占有度阈值min
_occ
(0≤min
_occ
≤1),对于一个k
阶的空间并置模式c
,当满足:1)PI
(c
)≥min
_prev
,2)OI
(c
)≥min
_occ
时,c
称为一个主导空间并置模式(dominant spatial co-location patterns, DSCPs).
主导空间并置模式挖掘的目的是发现同时满足min
_prev
和min
_occ
条件的所有并置模式,并按质量值对结果进行降序输出.
由于空间数据缺乏明确的事务概念,因此与传统的占有率定义不同,在空间数据上需要重新定义空间占用率(度)的概念,来衡量并置模式的完整性.本文提出一种等价关系——连通关系,给出了连通关系上的并置实例的划分,解决了空间并置实例及其邻域的重叠问题.基于模式的实例分区和实例分区邻域定义,我们提出了空间占有率(度)度量,用于评估并置模式的完整性并形式化了主导空间并置模式(DSCPs)挖掘问题.与事务数据的占有率度量一样,空间占有度度量也不满足单调或反单调性质,因此第3节将探讨空间占有度的2个上界,以提高DSCPs挖掘的效率.
此外,读者可能对DSCPs挖掘和极大并置模式挖掘之间的区别感兴趣.这2项工作在挖掘目的和方法上都有不同点.极大并置模式挖掘旨在挖掘所有并置模式的代表性模式,挖掘过程仍基于实例的邻近关系,根据极大并置模式集可推导出挖掘结果中的所有频繁模式,可以看作SCPs模式挖掘结果的压缩表示.DSCPs挖掘旨在找到一组同时考虑频繁性与完整性的高质量并置模式集,根据空间占有率及占有度的定义,尽管高占有度似乎意味着并置模式的阶数更高,但当并置实例的邻域中有大量邻居时,一个极大并置模式仍可能具有较低的空间占有率.此外,DSCPs模式的完整性的评估过程考察了并置实例邻域中其他特征实例对并置实例的影响,因此DSCPs的特征之间更可能存在强烈的关联.
通过将频繁性和完整性结合,DSCPs的挖掘结果在实际应用中更具有针对性,我们将在实验部分对DSCPs应用实例进行分析和阐述.
3 DSCPs挖掘算法
3.1 基本算法
本节中,我们首先提出一个基础算法对主导并置模式进行挖掘.
算法1.
主导并置模式挖掘基本算法(Basic_DSCPMA).输入:空间特征集F
、空间实例集S
、邻近关系距离阈值d
、频繁性阈值min
_prev
、占有度阈值min
_occ
、质量权重ω
;输出:主导空间并置模式集D
_set.
①NI
=find
_ins
_neighbors
(S
,d
);②P
=F
,k
=2,D
_set
=∅;③ while (P
-1≠∅)④C
=gen
_candi
_co
-location
(k
,P
-1);/
*引理1*/
⑤ for eachc
∈C
⑥T
(c
)=gen
_table
_ins
(NI
,c
);⑦ if (cal
_PI
(c
))≥min
_prev
⑧P
←c
;⑨TN
(c
)=find
_neighbors
(T
(c
),NI
);⑩ InitializeTP
(c
)←T
(c
);/
*对表实例进行连通关系上的划分*/












该算法的具体流程总结如下:
1) 将输入空间数据物化为定义2中给出的实例邻域模型(行①).
这个过程可以看作是文献[6]提到的星型邻居实例模型的一个变体.
2) 生成候选DSCPs(行②~④).
根据参与度的定义将所有特征初始化为1阶并置模式.
从k
-1阶频繁并置模式集P
-1(引理1)生成k
阶(k
>1)候选模式.
对于一个候选模式c
,如果c
的任一k
-1子模式不频繁,则该候选模式将被剪枝(行④).
3) 候选模式的频繁性过滤(行⑤~⑧).
由于空间邻近关系是对称的,因此可以直接从每个并置实例的第1个特征的实例邻域中获得二阶候选并置实例.
对于3阶以上的候选模式,则需要在生成表实例之前检查实例之间的团关系(行⑥).
接下来计算候选者的参与率和参与度,如果参与度超过阈值min
_prev
,将这个候选者加入k
阶频繁并置模式集P
(行⑦~⑧).

算法2.
并置实例划分算法(divide
_instance
(TP
(c
))).
输入:候选模式的表实例TP
(c
);输出:候选模式在连通关系上的划分TP
(c
),CIP
(c
).
①Flag
=True;② for each pair oftp
,tp
∈TP
(c
)③ if (tp
∩tp
≠∅)④Flag
=False;⑤ deletetp
,tp
fromTP
(c
);⑥TP
(c
)←Union
(tp
,tp
);⑦ if (Flag
)⑧CIP
(c
)←get
_ins
_set
(TP
(c
));⑨ returnTP
(c
),CIP
(c
);⑩ else





3.2 剪枝策略
在本节中,我们探索了空间占有度的2个上限以帮助修剪DSCPs的搜索空间,并设计了一种新的数据结构来提高DSCPs挖掘的效率.
3.2.1 并置邻居表
为了提高DSCPs挖掘过程的效率,缩减模式存储的冗余信息,本文设计了一种新的数据结构:并置邻居表,用于存储模式的并置实例邻域中的实例.基于这种新的数据结构,我们可以建立特征之间的映射关系,以加快对候选DSCPs的参与度和占有度的计算过程.
定义9.
并置邻居表.
给定一个k
阶并置模式c
,c
的并置邻居表(co-location neighborhood table,CNT
)由下列3部分组成:①c
的表实例邻域:TN
(c
)={RN
(l
),RN
(l
),…,RN
(l
)}及并置模式的索引;② 模式的特征集c
={f
,f
,…,f
}及出现在表实例邻域中的邻居特征集,记为NF
(c
)={f
+1,f
+2,…,f
},k
<o
,f
∈F
;③ 表实例邻域中的所有特征的实例个数统计.
如图3所示,并置邻居表列出了并置实例及其邻域中的所有实例,并置实例的邻居实例按其特征类型分组并存储为枚举结构.
在接下来的挖掘过程中,我们将展示这种新的数据结构如何在各个DSCPs挖掘阶段提高挖掘效率.

Fig. 3 Co-location neighborhood table图3 并置邻居表数据结构示例
3.
2.
2 基于参与度的剪枝剪枝策略1.
给定一个k
阶并置模式c
,c
的邻居特征集NF
(c
),对于任一k
+1阶候选模式c
+1=c
∪f
,f
∈NF
,若满足:|π
(CNT
(c
))|/
|T
(f
)|≤min
_prev
,则根据引理1,该候选模式可以被剪枝.
为在不生成表实例的情况下直接计算所有k
+1阶候选模式参与率及参与度,我们提出一组特征映射函数建立特征之间的映射关系.
在给出特征映射函数的定义之前,为方便描述,本文首先引入文献[44]中集合信息函数的定义,描述特征和并置实例邻域之间的关系.
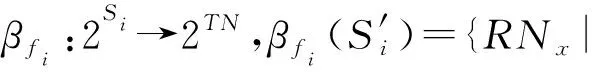
α
表示行实例集合对某一特征的实例集合的映射,函数β
表示某一特征的实例集对一组行实例集合的映射.
基于集合信息函数α
和β
,我们给出空间特征映射函数的定义.
定义10.
特征映射函数.
给定一个k
阶并置模式c
,其并置邻居表CNT
(c
)中的特征f
到f
的映射函数定义为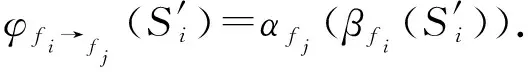
(8)
例如:对于频繁并置模式{A
,B
},该模式的邻居特征C
在并置邻居表CNT
({A
,B
})中的实例集合表示为:π
(CNT
({A
,B
}))={C.
1,C.
2,C.
3,C.
5},而与特征C
的实例位于同一并置实例的特征A
的实例可直接通过映射函数表示为φ
→({C.
1,C.
2,C.
3,C.
5})=α
(β
{C.
1,C.
2,C.
3,C.
5})=α
({l
,l
,l
,l
,l
})={A.
1,A.
2,A.
3,A.
5}.
给定一个k
阶并置模式c
及其邻居特征集NF
(c
),对于任意k
+1阶候选模式c
+1=c
∪f
,f
∈NF
(c
),c
+1的参与度可以直接计算为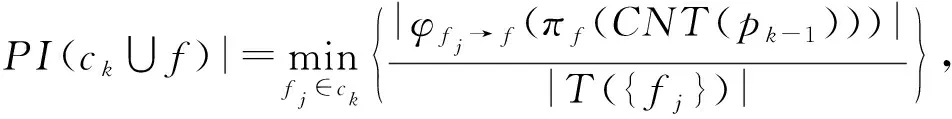
f
∈NF
(c
).
基于定义8,我们可以修剪频繁并置模式的搜索空间,并直接从并置邻居表CNT
(c
)计算所有以c
为前缀的k
+1阶候选模式的参与度而无需生成它们的表实例.
3.
2.
3 基于空间占有度的剪枝尽管空间占有度度量不满足单调性或反单调性,但我们仍然可以探索占有度度量的上限,以在挖掘DSCPs时减小搜索空间.
引理4.
空间占有度上界.
给定一个k
阶并置模式c
,c
的实例分区集CIP
(c
)={ip
,ip
,…,ip
},c
的实例分区邻域PN
(c
)={pn
,pn
,…,pn
},空间占有度OI
(c
)存在一个上界: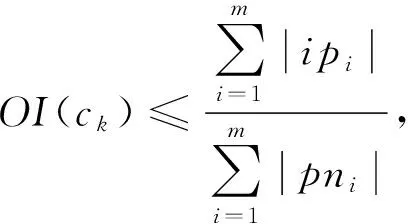
ip
∈CIP
(c
),pn
∈PN
(c
).
证明.

(9)



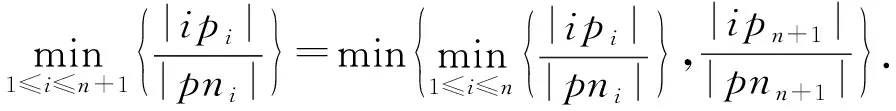
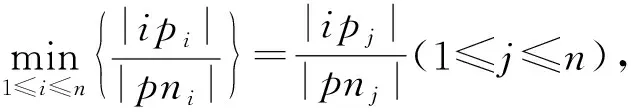
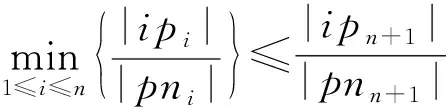
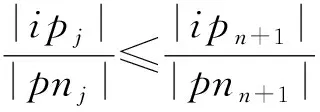
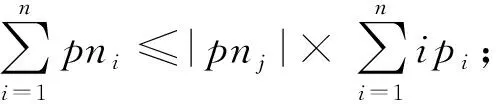


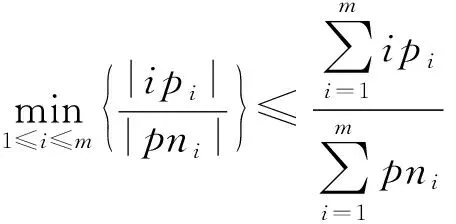
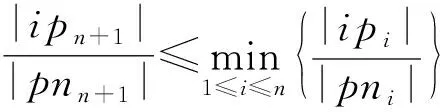

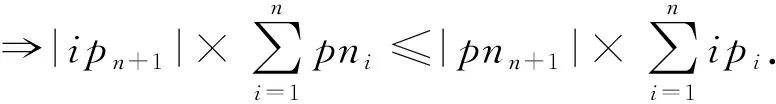
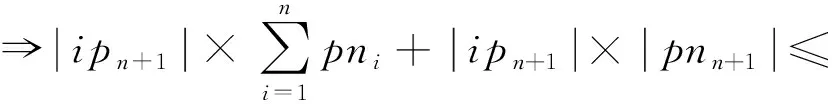

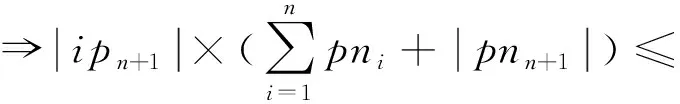
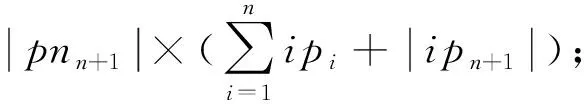

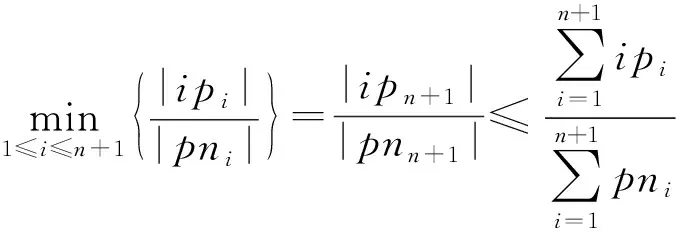
m
=n
+1时式(9)成立.
证毕.
剪枝策略2.
给定一个k
阶候选模式c
,c
的实例分区集合CIP
(c
)={ip
,ip
,…,ip
},c
的实例分区邻域PN
(c
)={pn
,pn
,…,pn
}及空间占有度阈值min
_occ
,根据引理4,若Upp
_occ
(c
)≤min
_occ
,则该候选模式可以被剪枝.
同时,基于c
的并置邻居表CNT
(c
),空间占有度上界Upp
_occ
(c
)可简单地通过下式直接计算:
基于引理4,DSCPs挖掘过程中生成实例分区邻域的过程可以通过剪枝策略2缩减候选模式搜索空间来减少计算开销.然而,表实例划分算法的递归过程仍然需要大量的计算.在实例分区过程之前对候选模式进行再一次过滤将能够进一步限制DSCPs的搜索空间,因此我们还为空间占有度计算了一个宽松的上限.
引理5.
宽松的空间占有度上界.
给定一个k
阶并置模式c
,c
的实例分区集CIP
(c
)={ip
,ip
,…,ip
},c
的实例分区邻域PN
(c
)={pn
,pn
,…,pn
},空间占有度OI
(c
)存在一个宽松的上界:
.
根据引理4:

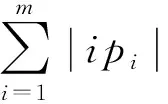
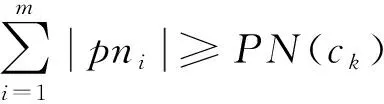

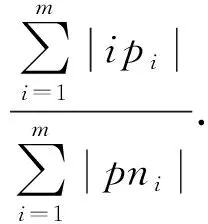
.
剪枝策略3.
给定一个k
阶候选模式c
,c
的实例分区集合CIP
(c
)={ip
,ip
,…,ip
},c
的实例分区邻域PN
(c
)={pn
,pn
,…,pn
}及空间占有度阈值min
_occ
,根据引理5,宽松的空间占有度上界,若Loose
_Upp
_occ
(c
)≤min
_occ
,则该候选模式可以被剪枝.
3.3 改进算法
根据3.2节中提出的并置邻居表数据结构和3个剪枝策略,本文提出DSCPs的改进挖掘算法,表示为DSCPMA_IA算法,该算法在候选模式的生成、频繁性过滤和及占有度过滤步骤中都进行了剪枝操作和基于并置邻居表结构的快速计算.算法3对改进的DSCPMA_IA算法进行了详细描述.
1) 生成候选并置模式.
对于频繁的并置模式p
-1,其从p
-1扩展的候选k
阶并置模式可以从p
-1的并置邻居表CNT
(p
-1)中进行选择.
根据剪枝策略1,我们通过测试直接从CNT
(p
-1)获得的每个扩展特征的参与率过滤k
阶的候选模式.
2) 频繁性过滤.
我们计算从CNT
(p
-1)扩展的k
阶候选模式的参与度.
根据定义10,我们可以计算k
阶候选模式的参与度,而无需生成候选表实例.
3) 完整性过滤.
使用剪枝策略3,候选模式c
可以通过其宽松的上界Loose
_Upp
_occ
(c
)进行过滤.
然后进一步使用剪枝策略2修剪DSCPs的搜索空间,从而避免消耗为空间占有率上界低于占有度阈值的候选模式生成进行表实例划分及实例分区的成本.
算法3.
改进的主导并置模式挖掘算法(DSCPMA_IA).输入:空间特征集F
、空间实例集点S
、邻近关系距离阈值d
、频繁性阈值min
_prev
、占有度阈值min
_occ
、质量权重ω
;输出:主导空间并置模式集D
_set.
①NI
=find
_ins
_neighbors
(S
,d
);②P
=F
,k
=2,D
_set
=∅;③ while (P
-1≠∅)④ for eachf
∈Neighbor
_Feature
(CNT
(p
-1))⑤c
=p
-1∪f
;⑥ if (|π
(CNT
(p
-1))|/
|π
(T
({f
}))|≥min
_prev
)⑦PI
(c
)=calculate
_PI
(CNT
(p
-1),f
);⑧ if (PI
(c
)≥min
_prev
)⑨P
←c
;⑩CNT
(c
)=generate
_CNT
(CNT
(p
-1),f
);
min
_occ
)



CIP
(c
));
PN
(c
));

OI
(c
),PI
(c
));
Q
(c
));







3.4 算法复杂性分析
本节比较了2种算法Basic_DSCPMA(以下简称BA)和改进的算法DSCPMA_IA(以下简称IA).2种算法都涉及5个阶段:1)将空间数据物化为实例邻域模型;2)生成候选DSCPs;3)候选模式的频繁性过滤;4)候选模式的完整性过滤;以及5)按质量值对DSCPs进行排序输出.整个算法过程的大部分计算时间用于2)~4)三个阶段.因此,下面我们将详细分析2种算法在生成候选DSCPs、候选模式频繁性过滤和候选模式完整性过滤3个主要算法过程中的时间及空间耗费.
1) 生成候选DSCPs过程.在BA中,该进程只根据引理1进行过滤,从而避免生成不必要的表实例.在IA中,对于频繁的并置模式p
-1,p
-1的并置邻居表CNT
(p
-1)提供剪枝和过滤所有由p
-1扩展的候选k
阶并置模式所需的信息,因此无需生成非频繁模式的表实例.
这个过程节省了不必要的并置候选参与度计算及其表实例的存储空间.
同时,从p
-1的并置邻居表CNT
(p
-1)生成p
的并置邻居表CNT
(p
)的过程无需再进行团实例检查,而可以通过特征映射函数,以CNT
(p
-1)的行号为索引生成新的CNT
(p
),该过程减少了大量团关系查询工作,生成新并置邻居表的过程仅需要O
(n
),n
为新并置邻居表的行数.2) 候选模式频繁性过滤过程.在IA中,对于每个候选c
=p
-1∪f
,f
的参与率可以直接从CNT
(p
-1)得到,其他特征在c
中的参与率可以通过映射函数计算,所以它只需要O
(m
),m
是含有实例邻居的扩展特征的并置实例的行数.因此,在改进算法中,我们节省了用于生成表实例和计算候选模式参与度的存储空间与计算量.3) 候选模式完整性过滤过程.我们计算空间占有度的上限来修剪搜索空间,基于存储参与表实例的特征投影的CNT
(p
-1)的最后一行,宽松的占有度上界可以被直接计算(剪枝策略2),复杂度为O
(1).我们开发的剪枝策略的计算成本是恒定的.因此,这些剪枝策略不仅可以在挖掘过程中修剪DSCPs的搜索空间,而且促进了算法的效率.4 实验评估
在本节中,我们在合成数据集和真实数据集上进行了实验,从多个方面评估了所提出算法的运行表现和挖掘效果.所有算法均使用Visual C#语言进行开发并在2.4 GHz、8 GB内存和Intel Core i7的PC机上运行.
4.1 实验数据集
我们在实验中使用3个真实数据集和一系列合成数据集来评估算法的效率和有效性.
1) 合成数据.合成数据集采用类似于文献[6]的方法生成合成数据.具体过程如下:首先,给定模拟数据的特征集合F
以及实例总数S
,并对特征集合中的特征依次编码,以便于下一步生成各个特征的相应实例;然后,给定一个平均阶数设定值k
(本文中设k
=5),使用泊松采样从特征集中生成阶数为k
的m
个模式作为初始模式(本文中设m
=20),在空间中为m
个初始模式随机生成C
个并置实例的实例集合(本文选取C
为实例总数S
的1%);之后,为每个初始模式的并置实例生成空间分布:为模拟空间实例的分布范围,D
×D
的区域被网格化为d
×d
大小的单元(d
为给定的邻近距离阈值),随机选择一个单元网格,在给定网格大小范围内进行随机采样,以生成一组并置实例的空间位置.接着,我们再将剩余的实例点随机分配特征类型,并在D
×D
的区域随机采样生成实例的空间位置.Dataset-1,Dataset-2和Dataset-3在1 000×1 000空间中生成,Dataset-4在2 000×2 000空间中生成,Datasets-5~Datasets-12在100 000×100 000空间中生成.请注意,尽管Dataset-2包含的实例比Dataset-3少,但由于分布范围更小,Dataset-2的密度高于Dataset-3.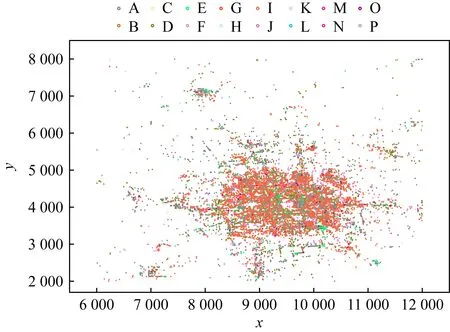
Fig. 4 Real-1 dataset distribution图4 Real-1数据分布
2) 真实数据.3个真实数据集的分布范围如图4~6所示.Real-1数据集是北京POI(point of interest)数据的空间分布数据集,如图4所示,该数据集包含大约26 546个实例和16个特征,其实例分布均匀且密集,不同特征的实例数量差异很大,成簇状分布.Real-2是云南“三江并流”保护区的植被分布数据集,如图5所示,包含25个特征和13 350个实例,在空间中呈块状分布.Real-3数据集是云南“三江并流”保护区珍稀植物数据集,如图6所示,包含32个特征,只有355个实例,在空间中呈明显的带状分布.表3出了我们实验中使用的所有真实数据集的分布范围和默认参数.

Fig. 5 Real-2 dataset distribution图5 Real-2数据分布
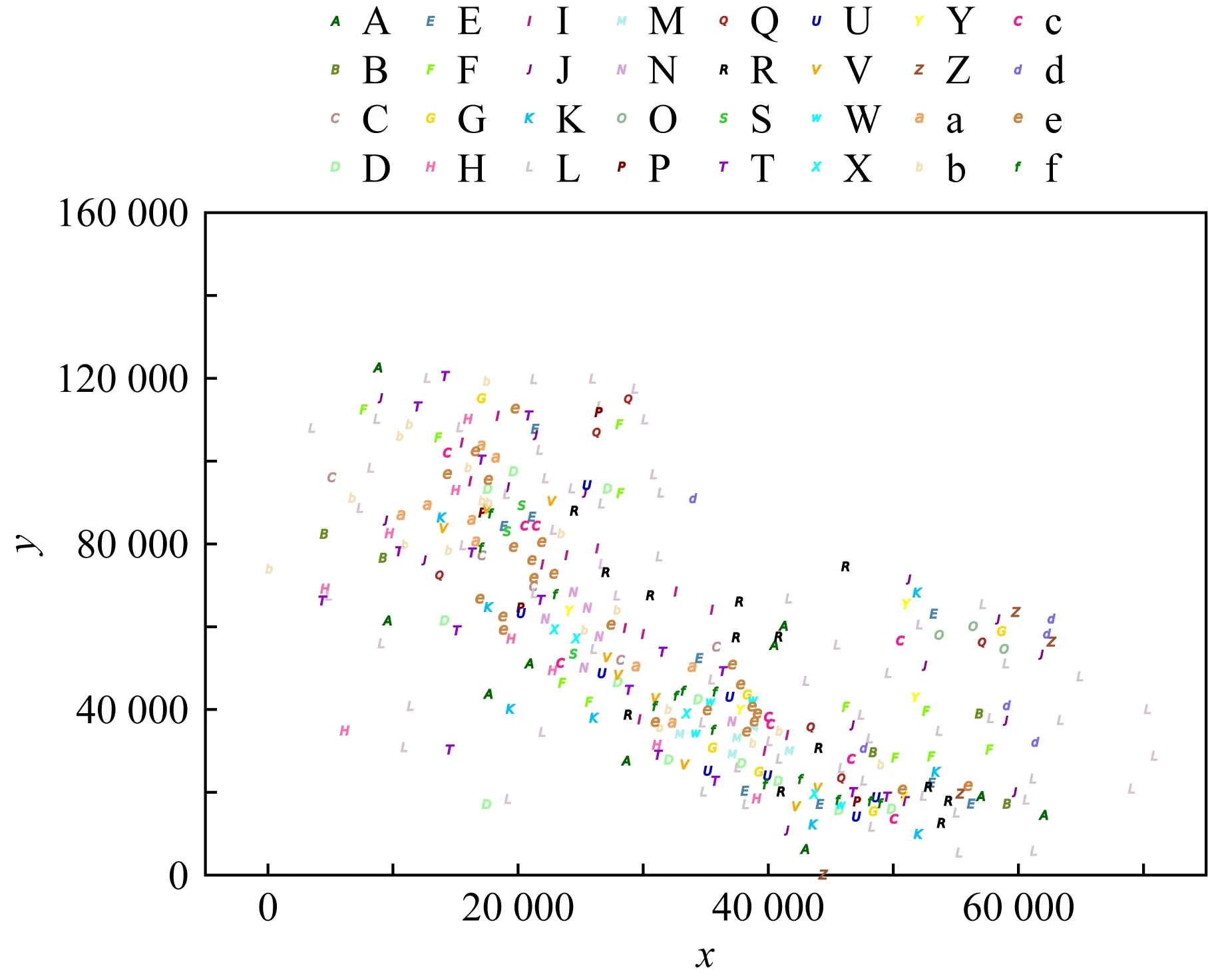
Fig. 6 Real-3 dataset distribution图6 Real-3数据分布
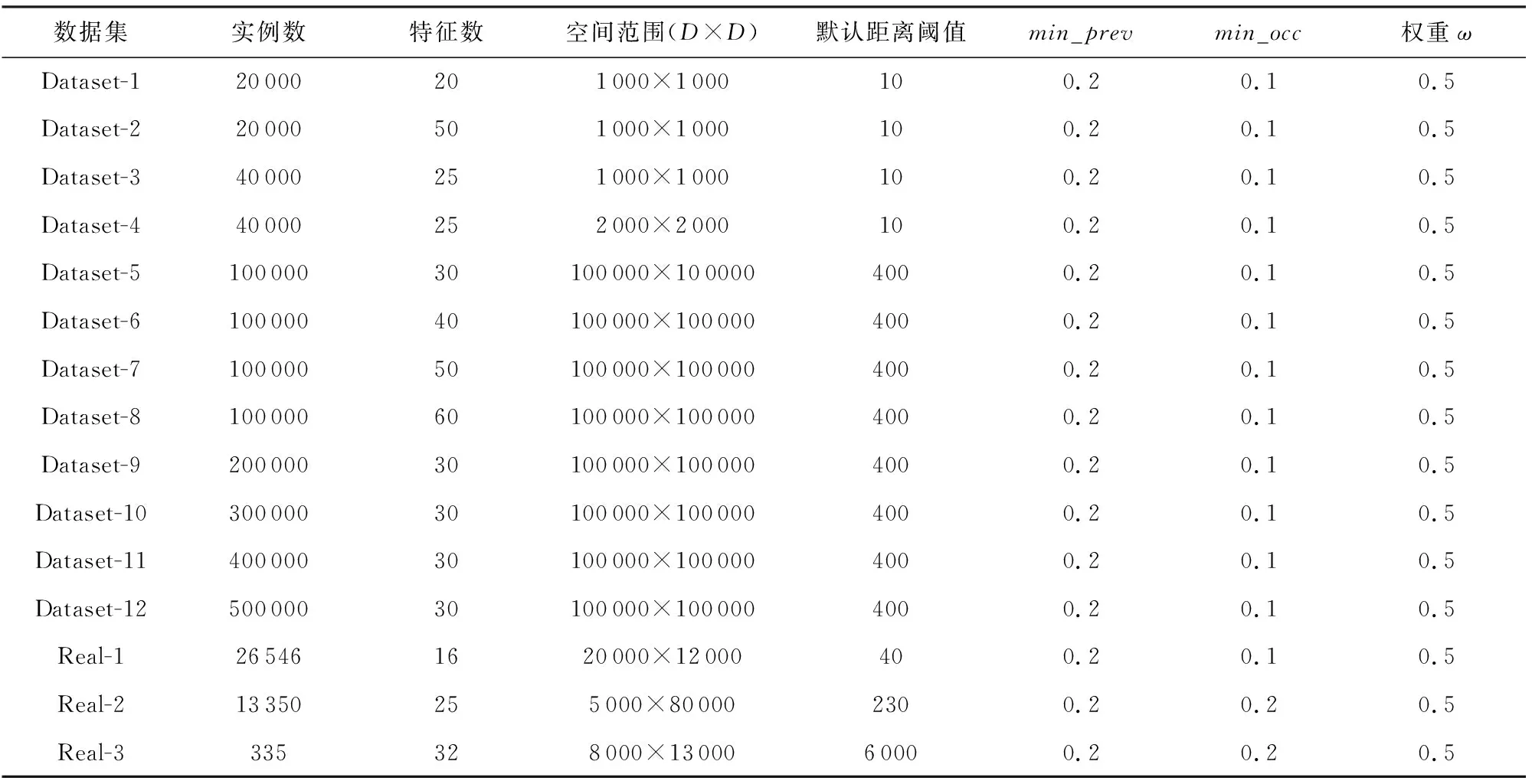
Table 3 The Experimental Data Sets and Default Parameters
4.2 算法性能评估
本节考察Basic_DSCPMA(以下简称BA)和改进的DSCPMA_IA(以下简称IA)这2种算法在一系列合成数据集上的效率.讨论在变化的距离阈值、最小频繁阈值、占有度阈值和权重参数上2种算法的性能表现.
1) 频繁阈值对算法的影响
BA和IA在4个不同的最小频繁阈值(min
_prev
)下分别在4个数据集上的运行时间比较如图7所示.BA和IA的结果分别用实线和虚线表示.不同的形状标记代表不同数据集的结果,例如BA-1展示了BA在Dataset-1上的性能.对于每个数据集,BA和IA的运行时间都随着min
_prev
的增加而减少.请注意,对于Dataset-1,Dataset-2,Dataset-3,在min
_prev
=0.6时BA和IA的运行时间相似,在min
_prev
=0.8时BA比IA更有效.这是因为较高的min
_prev
约束会导致生成较少的频繁并置模式,并且其中大部分是低阶模式.由于剪枝策略对2阶模式没有贡献,IA的计算开销反而大于BA.对于Dataset-1和Dataset-2,随着特征数量的增加,算法效率随之降低,所以Dataset-2的运行时间比Dataset-1长.Dataset-3的运行时间比Dataset-4长,表明效率主要受数据密度的影响.与实例数和特征数对算法的影响相比,数据密度对算法的影响更为显著.参与度阈值min
_prev
对算法性能的影响在Dataset-3上体现得尤为明显,因为低阈值和密集数据导致产生的大量高阶模式候选,因此剪枝策略性能优势更明显.min
_prev
越低,修剪策略越有效,尤其是在密集数据集上.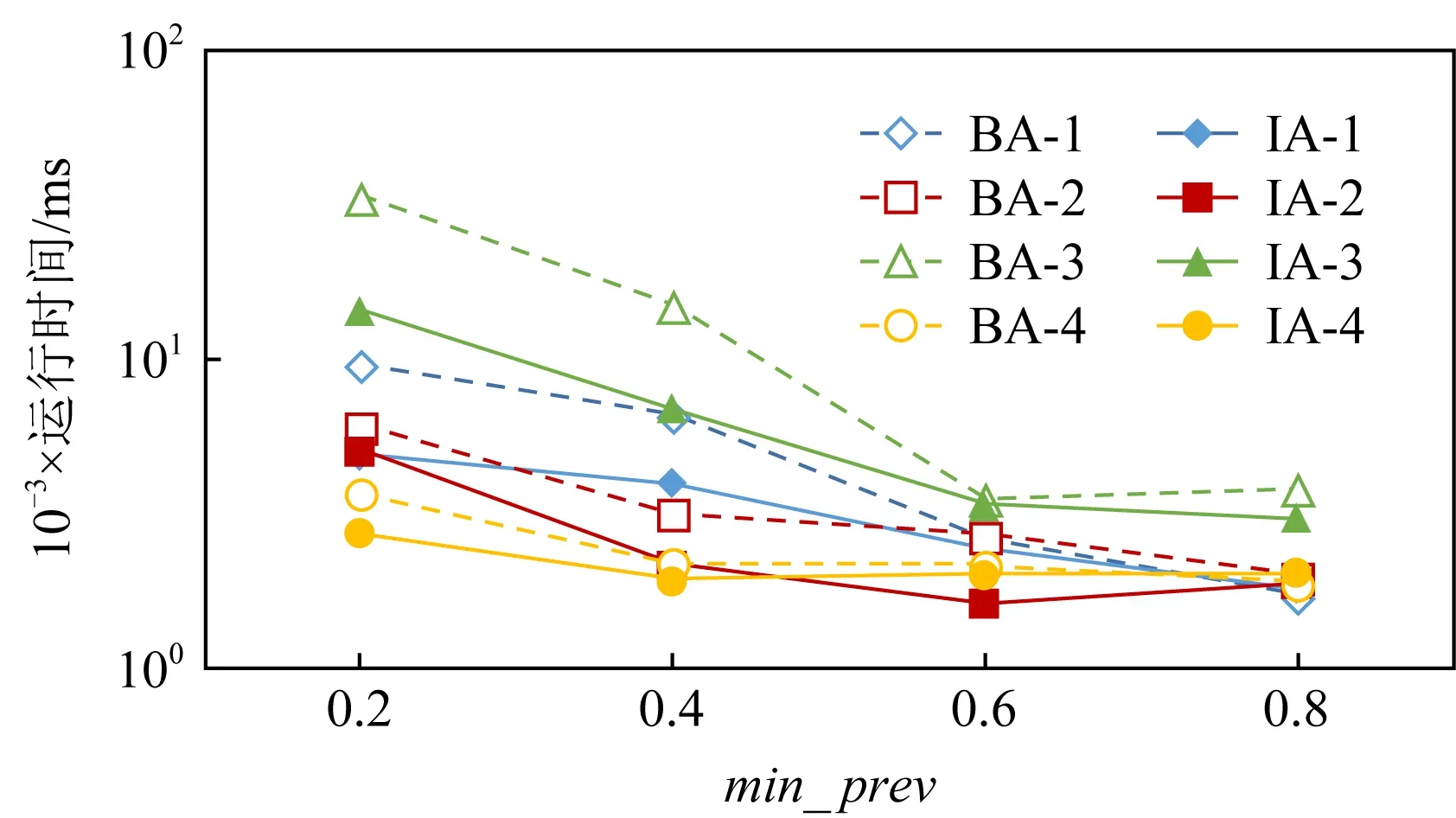
Fig. 7 The effect of min_prev variation on different data sets图7 频繁性阈值变化在不同数据集上对算法性能的影响
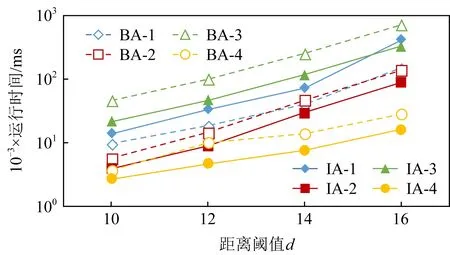
Fig. 8 The effect of distance variation on different data sets图8 距离阈值变化在不同数据集上对算法性能的影响
2) 距离阈值对算法的影响
图8展示了BA和IA在Datasets-1~Datasets-4上的运行时间分别相对于它们的距离阈值变化的比较.较高的距离阈值对算法性能的影响尤为明显,说明算法的性能主要受数据密度的影响.对于Dataset-1和Dataset-2,在d
=12时运行时间相似,这意味着当距离阈值较低时,BA和IA的效率差异很小.随着距离阈值的不断增加,由于IA中的一系列修剪策略有效地避免了为所有候选模式生成表实例,然后重复划分模式的过程.IA算法的性能逐渐变得比BA的效率更高.Dataset-3上的运行时间远大于Dataset-4上的运行时间,这表明所开发的算法对数据密度敏感,而实例数对算法影响不大.3) 空间占有度阈值对算法的影响
图9显示了BA和IA算法在Datasets-1~Datasets-4这4个数据集上的各自运行时间,相对于占有度阈值(min
_occ
)的变化.比较4个数据集上的运行时间,随着每个数据集上占有度阈值的增加,运行时间没有明显变化.这是因为占有度度量不满足单调性或反单调性.如果一个并置模式的参与度不小于min
_prev
,即使这个并置模式的占有度小于min
_occ
,仍然需要计算它的扩展模式的频繁性.对于每个数据集,IA比BA更有效,因为IA可以通过使用2个上限来过滤许多候选模式,并减少模式在连通关系上的划分过程的计算开销.对于Dataset-1和Dataset-2,Dataset-1的计算效率优于Dataset-2,因为Dataset-2中的特征数量比Dataset-1多,但效率差异并不明显.Dataset-3和Dataset-4的结果表明,在密集数据集上,IA算法的性能优势尤为明显.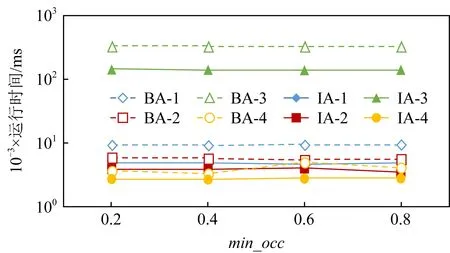
Fig. 9 The effect of min_occ variation on different data sets图9 不同数据集上占有度阈值变化对算法性能的影响
4) 算法的可伸缩性和扩展性
本节评估了BA和IA在不同情况下,即在合成数据集Dataset-5~Dataset-12上,通过在具有不同数量的空间实例和空间特征的数据上测试算法的可扩展性.
如图10所示,当空间实例数达到400 000时,BA与IA的运行时间开始呈指数增长,当空间实例数达到500 000时,IA的运行时间仍然明显优于BA.这意味着随着实例的增加,IA比BA更有效.而在前期数据量较小或数据分布较为稀疏时,IA的剪枝策略效果不明显.
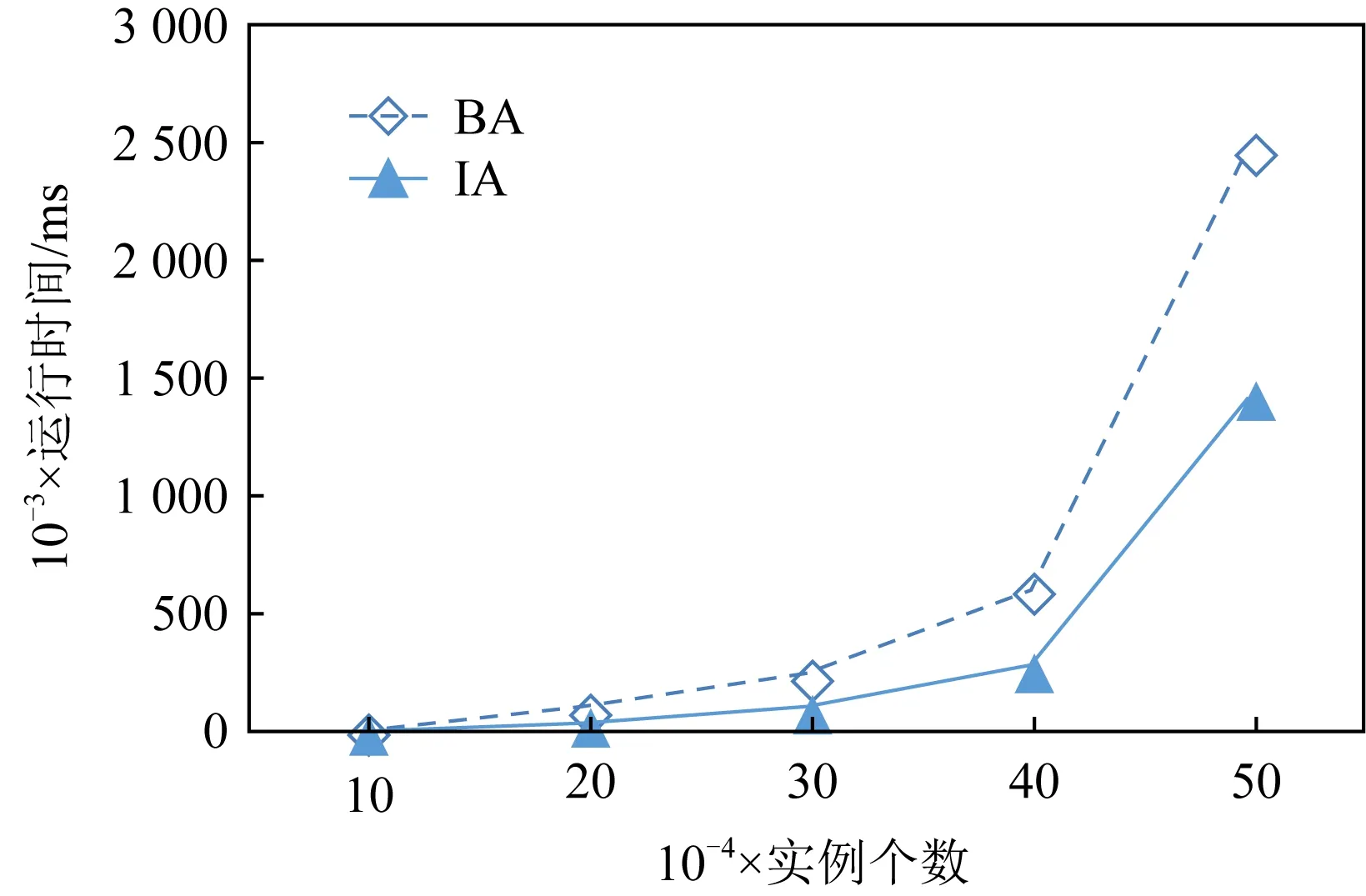
Fig. 10 The effect of the number of instance variation图10 实例个数变化对算法性能的影响
图11显示了BA和IA在随着特征数量的增加算法的运行时间的变化.在特征数较少时,单个模式的并置实例数量巨大,并置邻居表的快速生成和剪枝策略对候选模式的快速过滤使IA算法较之BA更高效.然而,当特征数量达到50时,由于空间实例的总数是固定的,单个特征的实例个数减少,则单个模式的行实例数降低,更难产生高阶的DSCPs.大量高阶候选并置模式在子模式频繁性检测阶段就直接被淘汰,因此运行时间快速减少,IA的性能则与BA相近.这说明并置模式挖掘的主要瓶颈在于生成高阶模式时的并置实例检查,而本文提出的剪枝策略及数据结构有效地促进了这个阶段算法的效率.

Fig. 11 The effect of the number of features variation图11 特征数变化对算法性能的影响

Fig. 12 The effect of min_prev on real-world data sets图12 真实数据集上min_prev对挖掘结果的影响
4.3 算法的有效性评估
频繁性阈值min
_prev
和距离阈值d
是影响算法效率的主要因素.在本节中,我们将讨论影响算法有效性的参数,并解释DSCPs挖掘在真实数据集上的实际应用.实验中使用了3个真实数据集来证明我们算法的有效性.与合成数据相比,真实数据集上的挖掘结果通常更有实际意义.空间占有度的概念可以看作是一个有趣的新度量和约束.根据DSCPs的定义,DSCPs需要满足频繁性和空间占有度约束,因此可以很容易地推断出在相同的min
_prev
和d
下,min
_occ
=0的DSCPs的挖掘结果与传统的频繁空间并置模(SCPs)的挖掘结果是完全一致的.因此,我们通过改变频繁性阈值(即min
_prev
)、占有度阈值(即min
_occ
)和权重(即ω
)来进行实验,以揭示参数设置对DSCPs挖掘结果的影响.1)min
_prev
对挖掘结果的影响如图12中的实验所示,我们设置min
_occ
=0来获得3个真实数据集上的SCPs,我们设置min
_occ
=0.
1来获得Real-1和Real-2数据集上的DSCPs结果.我们设置min
_occ
=0.2以获得Real-3数据集上的SCPs结果,其他默认参数如表3所示.在图12中,我们展示了具有不同min
_prev
的SCPs和DSCPs的挖掘结果,并记录了每个挖掘结果的不同大小模式的数量.可以看出,在每个数据集上,DSCPs和SCPs的数量都随着min
_prev
的增加而减少,并且在相同min
_prev
下,SCPs挖掘结果的数量远远多于DSCPs挖掘结果的数量.值得注意的是,随着min
_prev
的增加,SCPs结果中低阶模式的比例越来越高.对于每个数据集,高阶和低阶的DSCPs的数量都较少,而中等阶数的DSCPs的比例最大.2)min
_occ
对挖掘结果的影响图13展示了在相同频繁性阈值下,min
_occ
不同的优势SCPs的挖掘结果,其中min
_prev
=0.2,其他默认参数如表3所示.对于图13所示实验结果中的每个数据集,SCPs挖掘结果由一个堆叠列表示,其中min
_occ
=0,不同的条纹表示不同的模式大小.可以看出,对于每个数据集,DSCPs的数量随着min
_occ
的增加而迅速减少,尤其是对于较低阶的模式.相反,随着min
_occ
的增加,高阶模式继续保留在DSCPs结果中,表明即使空间占有度量不是严格单调的,模式阶数越高,其空间占有度可能越高.图13所示的实验结果可以进一步解释图12中SCPs和DSCPs挖掘结果之间的差异.对于每个数据集,即使一些高阶的模式被频繁性阈值过滤,但大多数低阶数的模式也被空间占有度阈值过滤.3) 权重参数ω
对挖掘结果的影响图14显示了使用不同权重(即改变ω
)的DSCPs挖掘结果的变化.根据定义7,权重参数ω
仅参与DSCPs挖掘过程的质量值计算部分.因此,它只能影响DSCPs结果的排序表示,而不会影响DSCPs挖掘结果.在图14所示的实验中,我们只选取了质量值最高的前20个DSCPs来观察权重对DSCPs挖掘排序结果的影响,其中min
_prev
=0.
2,min
_occ
=0.
1.
对于每个数据集,随着ω
的增加,前20位挖掘结果中,高阶的DSCPs的比例减少,而挖掘结果中低阶的DSCPs的比例增加.此外,在min
_prev
和min
_occ
相同的情况下,高ω
导致前20个DSCPs结果与按参与度排序的top-20个SCPs结果相似.例如,ω
=0.8时,图14(a)中的DSCPs结果中不同阶数的模式比例与图13(a)中的SCPs结果相似;当ω
=0.2时,不同阶数的DSCPs在图14(c)中min
_occ
=0.3时的比例相似.显然,ω
越高,参与度对DSCPs的贡献比重越大.这表明ω
的作用在于调整空间占有度和参与度对DSCPs质量的贡献以及对DSCPs挖掘结果进行排序,提高模式的可用性.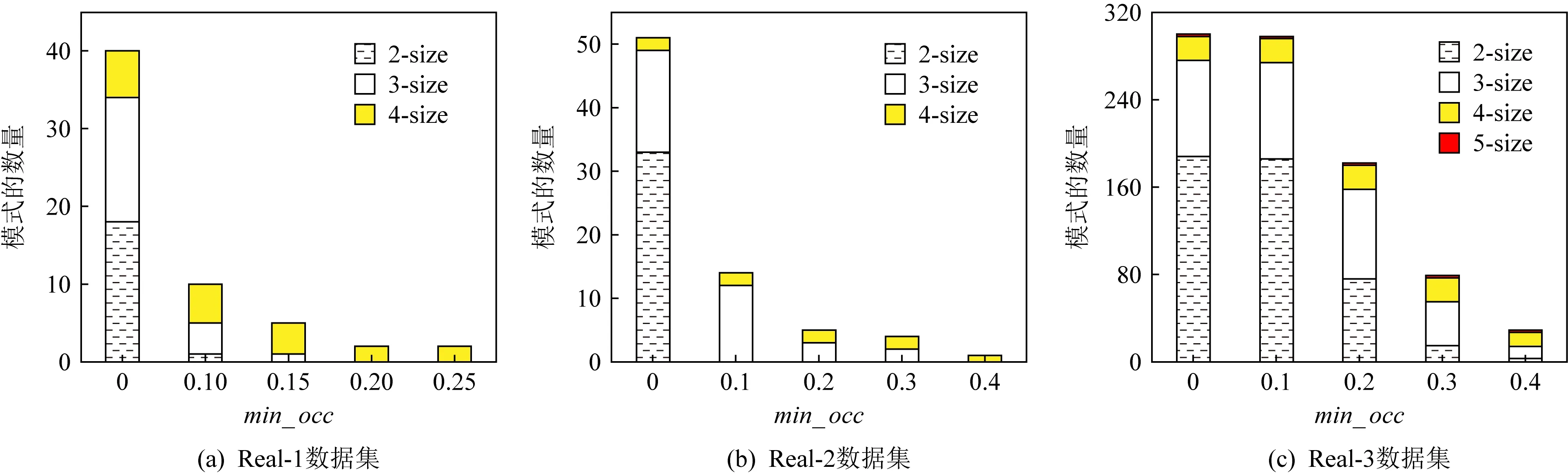
Fig. 13 The effect of min_occ on real-world data sets图13 真实数据集上min_occ对挖掘结果的影响
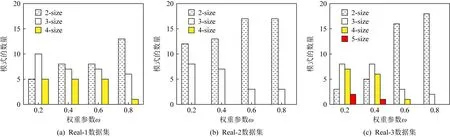
Fig. 14 The effect of ω on real-world data sets图14 真实数据集上ω对挖掘结果的影响
4.4 DSCPs挖掘方法应用实例分析
为进一步验证DSCPs挖掘方法在实际应用中的有效性,我们接下来介绍在珍稀植物数据集上的DSCPs挖掘应用实例分析.
表4列出了真实数据集Real-2(珍稀植物)上按质量值降序输出的top-5个DSCPs挖掘结果,表5列出了真实数据集Real-2输出的top-5个按参与度值降序输出的SCPs挖掘结果.
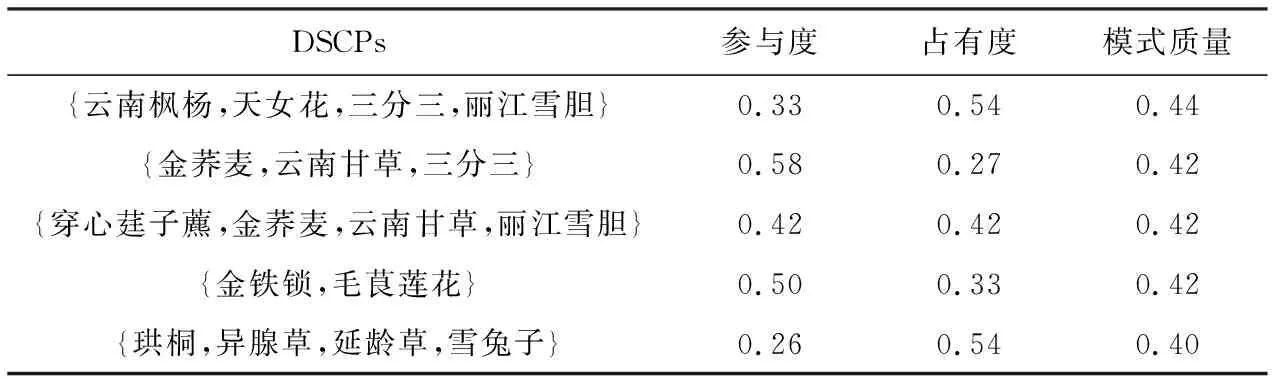
Table 4 The Results of top-5 DSCPs on Real-3 Data Set

Table 5 The Results of top-5 SCPs on Real-3 Data Set
与传统的频繁SCPs挖掘结果相比,表5中前5个参与度最高的模式都是低阶模式,且都是表4中出现的模式的子集.以表4中的模式{云南枫杨(A),天女花(D),三分三(I),丽江雪胆(M)}为例,该模式在空间中的分布如图15所示.可以看到模式的实例在其区域中都具有高的空间占有度,说明该组特征不仅在区域中具有很强的共存关系,且考虑了特征的多样性,向植物学家提供参考性更强的模式,便于植物学家进一步研究DSCPs代表的一组空间特征在区域中组成的生物群落及不同植物类型之间的相关性.
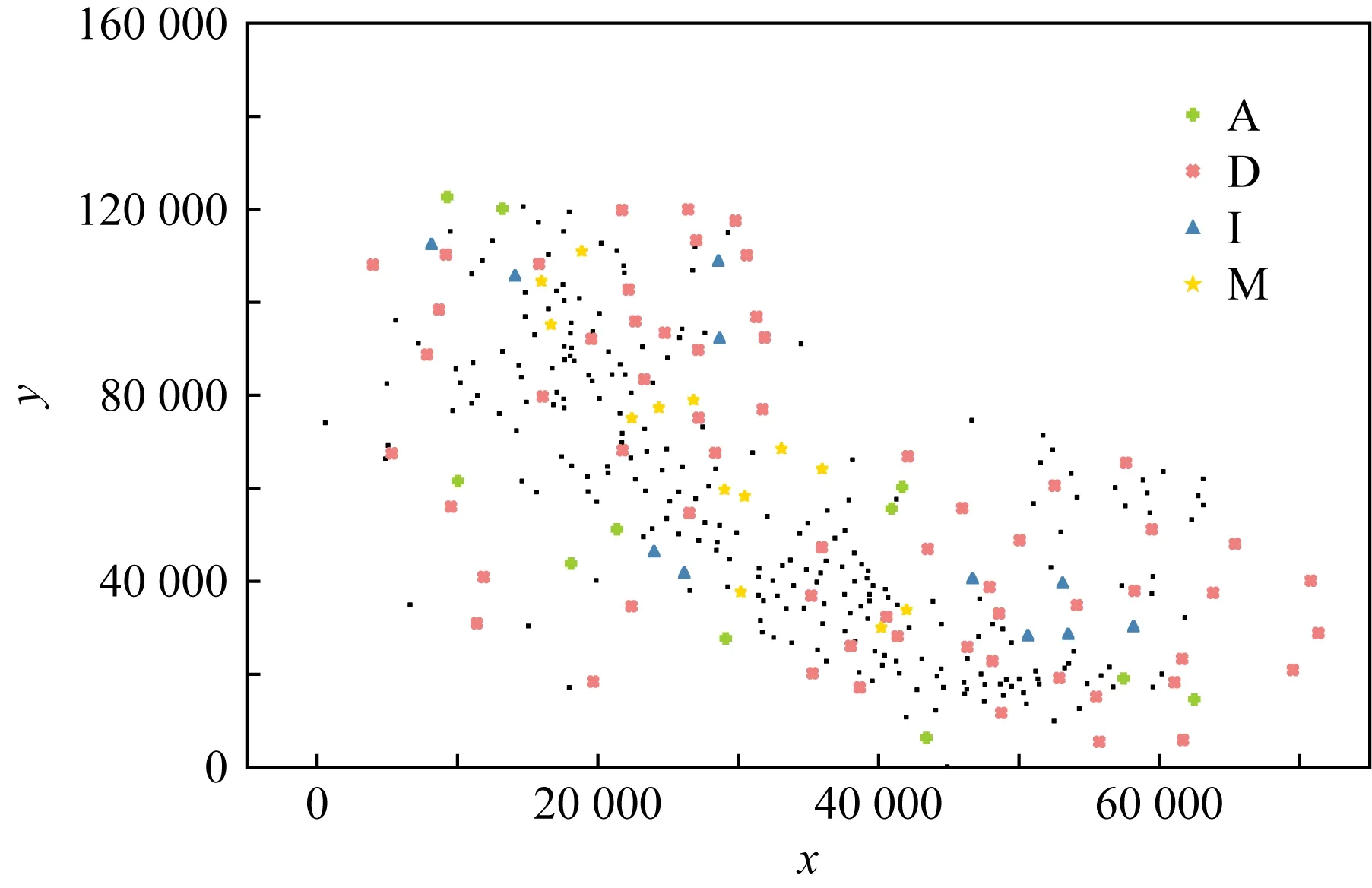
Fig. 15 Spatial distribution of a DSCP图15 一个DSCP的空间分布
5 结 论
目前,主流的空间并置模式挖掘的研究都将一组空间特征的实例在空间中共现的频繁性,即参与率-参与度度量作为兴趣度挖掘并置模式.然而,在一些并置模式的应用实例中,用户不仅对共置模式的频繁性感兴趣,而且还关注模式的完整性,希望得到该区域内较为全面的空间特征的并置信息.为解决以上问题,我们引入了一种新的空间占用度度量来评估共置模式的完整性,并通过结合模式的频繁性和完整性来制定主导空间并置模式(DSCPs)挖掘问题.为了解决经典并置模式(SCPs)挖掘过程中并置实例重叠问题,我们提出一种等价关系——连通关系将并置实例划分为不重叠的实例分区集.我们还设计了一种有效的算法 DSCPMA 来发现DSCPs,并通过探索空间占用度的2个上界和一个数据结构来实施一系列剪枝,有效地减少了DSCPs的搜索空间.最后,我们在合成数据集和3个真实数据集上评估了算法的效率和有效性.将DSCPs挖掘方法在珍稀植物数据集上的应用结果表明,DSCPs挖掘结果解释性更强,意义更明确,在实际应用中能够为用户提供更具有指导意义的知识.
作者贡献声明
:方圆提出了算法思路和实验方案,完成实验并撰写论文;王丽珍提出指导性意见并修改论文;王晓璇负责收集实验数据和完善实验方案;杨培忠负责完善实验方案和修改论文.
