多雷达实时引导数据的自适应加权融合算法研究

霍曾元 昝少东 邱德敏 冯志浩 祝敬乐 于春朋

摘要：针对目前国内地面测控站部署的多套雷达间数据共享实时性差、互引导数据利用率低等不足，为提高雷达互引导数据的精度和可靠性，提出了一种基于数据自适应加权融合算法的多套雷达实时互引导方法。该方法无需统计跟踪数据的统计特性等先验信息，直接依据当前时刻测量样本点进行分析计算，进而自适应分配各测量值权重，达到多组数据融合的目的。经仿真实验和实际工程验证，该算法融合效果较好，具有较强的实时性和鲁棒性，很大程度提升了雷达互引导功能的实用性。

关键词：实时引导；数据融合；支持度；鲁棒性

中图分类号：TP212.9文献标志码：A文章编号：1008-1739（2022）23-55-4

0引言

国内各卫星测控地面站内均部署有多套雷达测量设备，执行空间站等重大任务时，站内多套雷达需同时跟踪同一飞行器目标。飞行器可见弧段内，各雷达均基于轨道动力学模型事先计算出的理论弹道作为引导数据源，引导雷达捕获跟踪目标飞行器。当某套雷达理论弹道数据无效或飞行器偏离预定轨道时，则需要利用其他已经捕获跟踪目标的雷达的实时数据引导该雷达重新捕获跟踪目标。目前，已开发出雷达互引导软件，通过将某套雷达的跟踪原始数据复制迁移的方法初步实现多套雷达间的相互引导，但引导过程中经常出现数据中断、跳点和引入干扰等问题，导致实际引导效果较差，限制了多雷达互引导技术的应用。因此，如何有效融合多套雷达跟踪数据，提高融合数据的精度和鲁棒性，是提升多雷达互引导技术性能的关键。目前数据融合算法取得了很多研究成果，如文献[1]利用了总均方差最小条件下的拉格朗日定理，求解最优权值；文献[2-3]利用了模糊理论中的隶属度函数，调整权值分配，但这些融合算法均要求各测量值的先验知识和状态模型，计算量大，前置条件复杂，并不适用于要求引导数据高实时性、高鲁棒性的雷达跟踪系统。

为满足多雷达互引导技术的需求，本文提出了一种改进的自适应加权融合算法。该算法无需测量数据的各类先验知识，只针对多套雷达在某一时刻的一组数据进行分析计算，进而确定各套雷达测量数据相应的权重分配。与传统算法相比，该算法计算量小、流程简洁，通过算例仿真验证了本算法具有很强的实时性和鲁棒性。

1加权数据融合算法

传统的多源数据融合以文献[4]提出的算数平均法和文献[5-7]提出的最小二乘加权法较为常见。前者直接对测量数据进行算术平均；后者利用了数据源的先验精度信息，其融合决策结果具有统计意义上的最小方差。2种方法均是对各数据源赋予固定权重，计算量小，实施性强。缺点是当某个数据源数据出现异常（无数据或数据量级异常等）时，往往给出较大偏差甚至错误的融合结果。自适应加权算法[8]提高了融合决策的鲁棒性，但在生成融合权重时设定了门限值，并利用了二值判定方法，既提高了算法的复杂性也降低了测量值的利用效率。如何兼顾计算的快速性、数据的准确性和策略的稳定性是互引导数据改进工作的重点。

本文从实时性和鲁棒性出发，以某测控站内套不同精度雷达的测量数据（ =1，2，…， ）为例，提出一种改进的自适应权值分配策略。

该策略主要包含以下步骤：

將4种算法对方位角度（50°）进行100次采样，通过Matlab仿真计算，数据融合效果评价如表2所示。

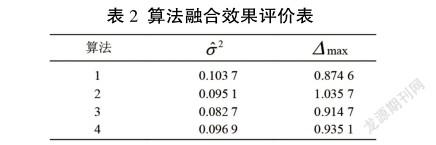
由表2可以看出，总体上，算法1～4融合结果精度较高，效果均表现较好，其中算法4最优，这是由于最小二乘加权融合算法是基于初始跟踪精度，且融合数据总方差最小的条件下推出的权重分配，而雷达测量数据由Matlab软件根据初始跟踪精度仿真生成，这些数据的统计特性与初始设定的跟踪精度严格一致，数据环境吻合度高，融合结果必然方差最小。

为进一步观察数据融合结果与原始测量数据间的关系，取前10次样本，4套雷达跟踪测量值的偏差以及4种算法产生的融合结果如图1和图2所示。

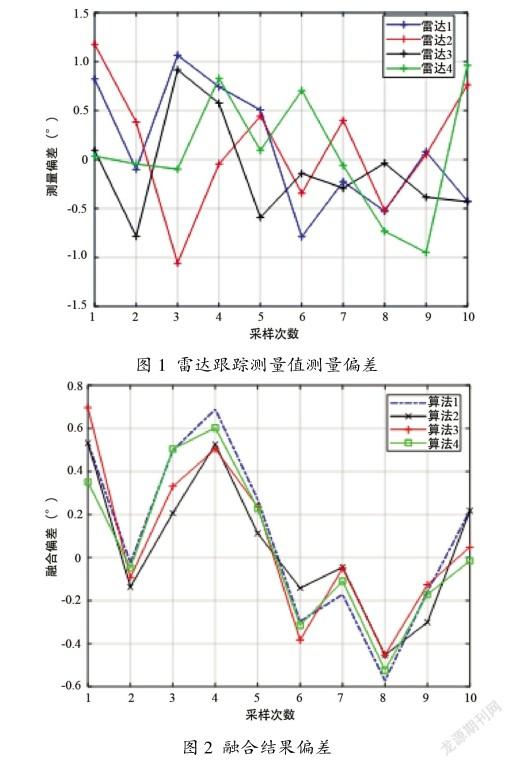
由图分析可得：

①算法4（即本文算法）与算法1相比，融合偏差更小，趋势更稳定。

②在第6次采样中，初始精度最高的雷达1给出的测量值偏差近乎最大，其所占权重最高，故算法3融合效果最差。

③在第4，8次采样中，测量值分别偏大、偏小，故所有算法融合结果都相应的偏大、偏小。

在目标跟踪过程中，由于外界干扰及雷达自身装备特性影响，容易出现部分雷达目标丢失或者设备故障带来的量测数据精度变差等情况，为比较各算法的鲁棒性，给出场景二。

场景二：假设各雷达初始方位跟踪精度同场景一，但在跟踪过程中，雷达1设备故障，方位跟踪精度突然下降至20，将4种算法对方位值（50°）进行100次采样，通过Matlab仿真计算，数据融合效果评价如表3所示，4种算法产生的融合结果偏差如图3（取前10次样本）所示。

由表3和图3可以看出：

①算法2和算法3均表现较差，融合结果已不可用，其中算法3将初始精度最高的雷达1量测数据赋予了最高的权重，因此雷达1跟踪精度变差时，它的融合效果最差，这也验证了场景一的结论。

②算法1和算法4表现较好，其中算法4融合效果最优，稳定性最好。后经过大量实验验证，在单套雷达设备故障，跟踪测量值精度发散时，算法4融合结果方差仍能维持在0.4左右，而算法1融合结果方差下降至10以下，进一步说明算法4比算法1具有更强的鲁棒性。

通过上述2个仿真场景中代表固有权重的算法2和算法3融合效果前后对比，可得初始精度的分析使用可提高数据融合效果，但降低算法的鲁棒性。为二者兼顾，文献[9]对固有权重和测量权重的加权占比系数做了简单分配。其实系数分配原则需要与实际应用工程相匹配，如本文的互引导数据更强调算法的鲁棒性，即互引导数据作为备用数据源，当雷达跟踪异常时才会启用。因此算法内权重的组成不需要包含使用初始精度推算的固有权重，即固有权重系数占比为零。当然，实际其他工程中也可以降低算法的部分自适应性，将2个加权占比系数作为开放参数，依据不同应用场景实时调整。

3实测数据验证

为贴合实际应用场景二，对某地面站内4套雷达（跟踪精度全部为0.015°）的某一弧段数据进行融合实测，分别用4种算法计算融合弹道。为便于比较融合效果，让精度最高的雷达测量弹道近似测量真值，择机选择另一套雷达，让其跟踪测量弹道疊加方位、俯仰均为5°的偏差，各算法融合结果如图4所示。

由图4可以看出，代表本文算法的绿色线条最接近真实轨迹，数据精度最高，融合效果最优。

4结束语

本文从提高地面测控站雷达互引导功能的实用性角度出发，提出了一种改进的自适应加权融合算法。通过系统仿真和实际工程应用，证明该算法在预设场景中雷达出现异常时，可有效避免互引导数据出现断点、野值等风险，且该算法数据处理的实时性更好，在雷达测量领域具有良好的推广应用价值。

参考文献

[1]张阳，沈明霞，孙玉文，等.基于多传感器自适应加权融合的温室信息系统[J].传感器与微系统，2014，33（6）：100-103.

[2] WANG J H， GAO Y. Multi-sensor Data Fusion for Land Vehicle Attitude Estimation Using Fuzzy Expert System[J]. Data Science Journal， 2006（4）： 127-139.

[3]胡振涛，刘先省.基于相对距离的一种多传感器数据融合方法[J].系统工程与电子技术，2006（2）：196-198.

[4]陈忠德，蒋静坪.一致性多传感器数据融合方法的改进[J].传感器技术， 1995（5）：52-55.

[5]凌林本，李兹刚，陈超英，等.多传感器数据融合时权的最优分配原则[J].中国惯性技术学报， 2000，8（2）：36-39.

[6]刘建书，李人厚，常宏，等.基于相关性函数和最小二乘的多传感器数据融合[J].控制与决策， 2006（6）：714-716.

[7]赵华哲，李强，杨家建.基于最小二乘原理多传感器加权数据融合[J].微型机与应用， 2013， 32（12）：7-10.

[8]邢晓辰，蔡远文，任江涛，等.一种考虑传感器精度的数据自适应加权融合算法[J].电讯技术，2015，55（10）：1079-1086.

[9]熊彦铭，李世玲，李军，等.多传感器时间控制系统的数据融合新算法[J].弹箭与制导学报， 2012， 32（1）：171-174.