基于贝叶斯优化的中庭热压通风性能分析与设计①
朱赛鸿,刘诗雨,姚胜,连天成
河北工业大学 建筑与艺术设计学院,天津 300130
中庭作为一种建筑空间,在满足交通、采光等功能的同时,其高大的空间所形成的“烟囱效应”可以促进大进深建筑的自然通风,对于提升室内空气品质、改善热环境有重要作用,目前广泛应用于各类公共建筑中.
沈焕杰[1]研究认为当核心式中庭建筑四面外墙均开窗,且中庭仅顶面与外界直接相通时,影响热压通风性能的参数将不只是进出风口面积及高度差. Ali等[2]重点关注了中庭壁面倾斜角度对热压通风的影响,指出在建筑顶层会出现热风由中庭进入周边房间的现象,导致建筑上下层不能获得相似的通风性能,并提出了最佳的壁面倾斜角度以最小化建筑上下层通风性能的差异. 代语[3]研究了中庭所处平面位置以及与周边房间交界面的开口面积对热压通风的影响. 曾琳雯[4]针对重庆商业建筑中庭的平面形状、面积占比、剖面形态和顶界面等要素,借助CFD模拟分析了各要素对中庭热压通风风速、温度等的影响. Abdullah等[5]研究了屋顶形式及中庭顶面开口形式对中庭通风性能的影响.
综上,由于通风性能涉及参数较多,关于热压通风性能的研究大多采用的是单参数或者部分参数局部分析,而不能对参数空间进行全局耦合分析与优化. 针对以上问题,本研究提出基于贝叶斯优化的中庭热压通风性能分析及设计方法,主要研究内容包括:1)主要参数敏感性分析与设计参数筛选. 2)耦合参数化设计平台、贝叶斯优化与CFD模拟软件对设计参数进行优化.
1 研究对象
1.1 典型模型
本研究以最常见的核心式中庭建筑为研究对象,如图1所示. 中庭平面为矩形,位于建筑核心位置并与四周房间连通,外墙均匀开窗,室外空气由外窗进入建筑使用空间,通过中庭与周边房间交界面的开口进入中庭空间,在热压的驱动下由中庭顶部排出(图2). 建筑模型占地面积为2 000 m2,层高为5 m,通过窗宽及开窗间隔可控制开窗面积大小,结合调研数据确定的主要设计参数的值域如表1所示.

图1 核心式中庭建筑典型模型

图2 核心式中庭建筑气流组织图

表1 建筑设计参数及范围
1.2 评价指标
既有相关研究多从舒适度方面对自然通风进行研究,缺少针对热压通风导致的上下层通风差异的评价,因此本研究选取温度、风速及不均匀度作为衡量热压通风的性能指标. 具体地,提取各层1.5 m高处参考平面的温度、风速值为输出结果计算相应的平均值,并使用式(1)计算各自的不均匀度.
(1)
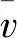
2 研究方法
2.1 基于参数化建模的CFD数值模拟
真实建筑场地环境、设备参数、运行情况等会对设计参数产生极大影响,致使敏感性分析对样本的需求量大,考虑到经济成本和时间成本,本文基于参数化建模平台Grasshopper(GH)及其流体仿真插件Butterfly(BF),在参数化平台中实现参数采样、模型修改以及流体仿真的工作. 拉丁超立方采样(LHS)可以使样本分布更加均匀并避免对某一区域重复抽样,以更小的计算量覆盖参数空间的概率分布[6],因此利用LHS对参数进行抽样组合,并根据采样的参数值修改建筑模型,以调用CFD仿真进行批量计算,样本获取流程如图3所示. 仅考虑热压作用下的自然通风,采用RNGkepsilon湍流模型及BuoyantSimple求解器,最大迭代步数2 000,收敛残差10-3,并依据《公共建筑节能设计标准GB 50189-2015》及相关文献[7]设定边界条件,如表2所示.

表2 CFD相关参数设定

图3 样本获取流程图
2.2 敏感性分析
影响建筑中庭热压通风的因素众多,而过多的参数会降低贝叶斯优化效率,故在进行贝叶斯优化之前需要对参数进行敏感性分析,并筛选出主要的敏感参数. 为保证分析的可靠性,本文选取两种敏感性分析方法:偏相关系数法和基于树状高斯过程(TGP)的Sobol法.
2.2.1 偏相关系数法
偏相关系数法是在消除自变量间的相关性影响后,所获得的自变量与因变量之间的相关程度,经常用来衡量各变量的相对重要性[8]. 偏相关系数法更适合分析自变量间存在相关性的问题,但其只能分析各变量单独作用时产生的影响,并且只适用于线性模型. 当变量i同时与变量j和k存在相关性,在消除变量k的影响后变量i和j的相关性,即变量i和j的偏相关系数,可用各变量间的相关系数通过式(2)进行计算.
(2)
式中,rij为变量i和j的相关系数;rij,k为i和j的偏相关系数.
2.2.2 基于树状高斯过程的Sobol法
高斯过程在处理小样本、高维度、非线性的回归问题上具有良好的适应性[9],决策树基于分而治之的思想对于回归问题是一个简单有效的方法,TGP是高斯过程和决策树的结合,具有两者的优点,适用于非线性和非静态回归模型[10]. 本文利用R语言读取建筑设计参数和仿真结果,并使用TGP软件包[11]进行Sobol敏感性分析,具体步骤:1)根据抽样数的建筑参数及模拟结果,利用TGP建立预测模型;2)利用Sobol法对模型结果进行敏感性分析.
主效应和全效应是敏感性分析结果的两个指标. 主效应用于表征参数单独变化时对结果方差的贡献,并使用一阶敏感性指数来度量贡献水平,全效应则指各参数在与其他参数交互作用的情况下对结果方差的贡献. 具体计算公式为
(3)
(4)
式中,Si为第i个参数的一阶敏感性指数;V表示为模型输出(风速或温度等评价指标)的总方差;Vi为第i个输入参数的一阶方差;Ti为第i个参数的全效应;Xi为输入参数;X-i为除Xi外其余输入参数;Y为模型输出. 通过Si对重要参数进行敏感性排序,通过Ti来筛选对模型结果影响不明显的参数,Ti与Si之差反映参数间的交互作用,如果差值较大,说明参数间交互作用明显[12].
2.3 贝叶斯优化
对中庭热压通风进行优化,可以视为寻找最优参数集θ使得目标函数f达到最大的非线性优化问题[13]. 贝叶斯优化核心是贝叶斯定理,此外还包含两个关键部分:概率代理模型和采集函数.
2.3.1 概率代理模型
概率代理模型用于代替评估代价高昂的目标函数,通过不断迭代获得观测值,对先验概率进行修正,获得包含观测信息的后验概率分布[14]. 高斯过程因其灵活性和可扩展性是贝叶斯优化中广泛应用的概率代理模型,其先验均值对后验分布的准确性几乎没有影响,故一般设定为0[13];协方差指定了未知目标函数的平滑性和振幅,表征2个计算点的相似性,Matérn协方差函数簇是一类高度灵活的协方差函数,表达式为
(5)
式中,v为平滑参数,l为尺度参数,Kv为第二类变形贝塞尔函数. 参照邓帅[15]的研究,本研究分别令v=2.5,l=1.
2.3.2 采集函数
采集函数是根据概率代理模型的后验结果进行构造的,通过最大化采集函数来选择下一个评估点,采集函数应兼顾提高目标函数的均值和减小目标函数的不确定性. 当采用高斯过程作为概率代理模型时,通常使用的采集函数为提升概率(PI)、期望提升量(EI)和置信上边界(UCB). 本文选择EI作为采集函数,其能更好地整合提升概率与提升量大小.
2.3.3 优化框架
贝叶斯优化是一个迭代过程,不断选择评估点并对评估点进行观测,达到最优化目标函数的目的. 本文通过开发Grasshopper平台下的贝叶斯优化工具,结合参数化建模和CFD数值模拟实现计算机对建筑通风性能的自动优化,具体流程如图4所示.
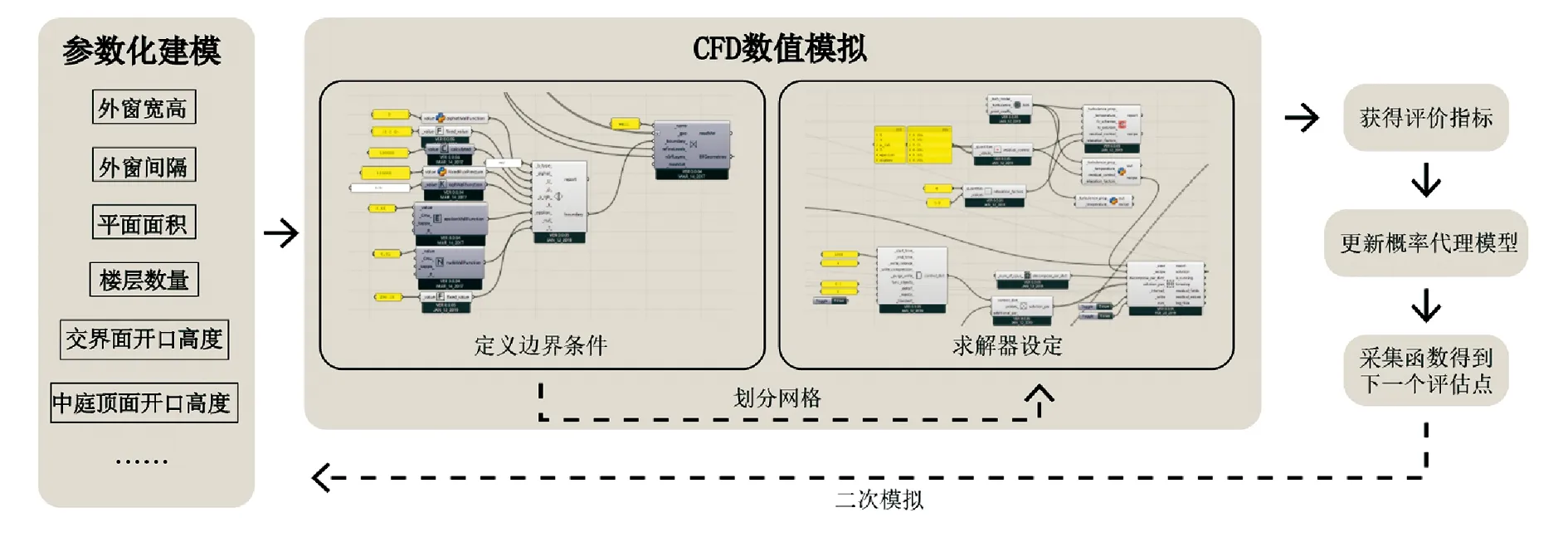
图4 贝叶斯优化流程图
3 敏感性结果分析
基于参数化平台的CFD工作流程,使表1中每个建筑设计参数至少变化10次,以200个建筑案例作为样本进行分析,4个性能指标的分布如图5所示.

图5 性能指标样本分布
可以看出,建筑设计参数会显著影响建筑中庭的通风性能,平均风速大部分在0.3 m/s左右. 风速不均匀度反映建筑内风速的离散程度,图中风速差异大部分集中在0.25 m/s左右,同时在0.2 m/s时会发生剧烈下降. 平均温度离散程度较高,大部分在294.5 K至296 K之间. 温度不均匀度描述建筑内温度的离散程度,由图5可知大部分建筑在1.25 K左右波动,但是仍有一部分建筑的温度波动在2 K和0.75 K左右. 同时比较各箱型图可知,相比于其余3个性能指标,建筑设计参数对平均温度的影响更为显著.
3.1 平均风速
偏相关系数法分析结果如表3所示,显著性检验显示中庭面积占比P2、开窗面积P7与平均风速在0.01水平上显著相关,交界面开口面积P6与平均风速在0.05水平上显著相关,其余各参数与平均风速没有相关性,对比图6可知偏相关分析及TGP敏感性分析中的主效应结果基本一致.
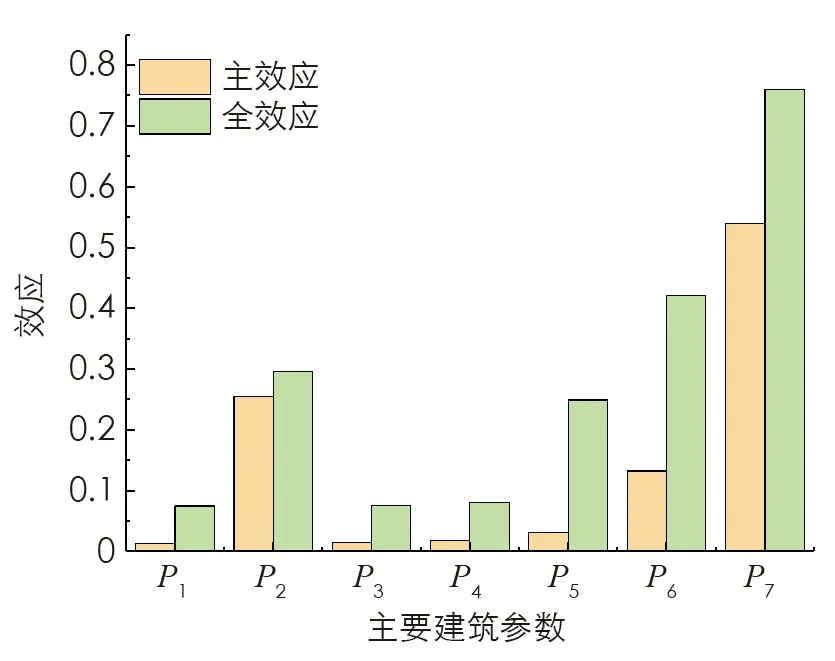
图6 平均风速TGP分析结果

表3 平均风速偏相关分析结果
结合图7所示的各参数影响趋势图来看,开窗面积P7为最敏感参数,引起平均风速50%左右的波动;中庭面积占比P2,引起平均风速25%的波动;交界面开口面积P6引起平均风速15%的波动. 对比各参数的主效应和全效应可知,P5,P6和P7之间相互作用明显,特别是交界面开口面积P6的主效应仅为10%而全效应达到40%,在实际设计时需要着重考虑三者间的合理组合. 从影响方向上看,平均风速与开窗面积P7呈正相关,与中庭面积占比P2及交界面开口面积P6呈负相关,说明当中庭面积增大时应增加开窗面积并减小与中庭交界面的开口面积以保证室内风速的舒适性. 从影响趋势上看,当交界面开口面积P6取值较低时对平均风速的影响较小,当继续增大取值时与平均风速开始呈非线性关系,其余主要参数与平均风速均呈线性关系.

图7 主要参数对平均风速的影响趋势图
3.2 风速不均匀度
风速不均匀度偏相关系数分析结果和TGP分析结果分别如表4和图8所示. 对比偏相关和TGP敏感性分析中的主效应结果,同时结合偏相关分析中显著性检验结果,两者敏感性排序基本一致,共有P7,P6,P5,P4及P2共5个敏感指标,其中开窗面积P7为最敏感参数,由图9可知引起风速不均匀度近20%的波动,交界面开口面积P6、天窗开口面积P5、天窗开口距顶层距离P4及中庭面积占比P2的敏感性较为接近,引起风速不均匀度近10%的波动.P2,P5及P6的全效应提升明显,说明三者的相互作用对风速不均匀度的影响极大. 从影响方向上看,风速不均匀度与开窗面积P7、交界面开口面积P6及中庭面积占比P2呈负相关,与天窗开口面积P5呈正相关,此外风速不均匀度与交界面开口面积P6呈非线性关系,与其余参数均呈线性关系.

表4 风速不均匀度偏相关分析结果

图8 风速不均匀度TGP分析结果

图9 主要参数对风速不均匀度的影响趋势图
3.3 平均温度
平均温度偏相关系数分析结果和TGP分析结果分别如表5和图10所示. 对比偏相关分析及TGP敏感性分析并结合显著性检验,敏感性排序依次为P7,P6,P2及P5. 由图11可知开窗面积P7为最敏感参数,引起平均温度近60%的波动;交界面开口面积P6次之,引起平均温度近30%的波动;中庭面积占比P2和天窗开口面积P5的敏感性水平相近,引起平均温度近10%左右的波动. 对比全效应和主效应发现各参数主效应没有明显提升,说明各参数对于平均温度的影响并不会相互制约. 从影响方向及趋势上看,所有参数均与平均温度呈线性负相关.

表5 平均温度偏相关分析结果

图10 平均温度TGP分析结果

图11 主要参数对平均温度的影响趋势图
3.4 温度不均匀度
温度不均匀度偏相关系数分析结果和TGP分析结果分别如表6和图12所示. 对比偏相关分析及TGP敏感性分析并结合显著性检验,两者敏感性排名基本一致,最敏感参数为交界面开口面积P6,由图13可知引起温度不均匀度近40%的变化;开窗面积P7及中庭面积占比P2敏感性水平相近,引起温度不均匀度近30%的变化;天窗开口面积P5为最不敏感参数,只引起温度不均匀度近10%的变化.P5,P6及P7全效应提升明显,说明三者对于温度分布情况的影响会相互制约,在设计时需要合理组合. 从影响方向及趋势上看,所有参数均与温度不均匀度呈线性负相关.

表6 温度不均匀度偏相关分析结果

图12 温度不均匀度TGP分析结果

图13 主要参数对温度不均匀度的影响趋势图
3.5 敏感参数筛选
依据上述分析,建筑纵横比P1与中庭纵横比P3为不敏感参数,天窗开口距顶层高度P4仅对风速不均匀度产生较小的影响,说明在建筑高度确定的情况下,略微提升中庭高度并不能提高中庭通风性能,故在设计过程中可以忽略以上参数对通风性能的影响. 中庭面积占比P2虽然对平均风速有较大影响,与其余参数的耦合会对风速不均匀度产生较大影响,但对于温度方面影响较小,同时中庭面积还受限于实际建筑使用面积的影响,设计空间受到一定制约,故在实际设计过程中也可以忽略其对通风性能的影响;天窗开口面积P5的主效应显示其对通风性能的指标影响很小,但全效应提升明显,说明与其余参数耦合效应强烈;交界面开口面积P6和开窗面积P7的主效应水平较高,并且全效应提升同样明显,说明参数不仅自身对通风性能有极大影响,与其他参数间互相作用的效果同样明显,故在实际设计中应重点关注并寻求最佳的参数组合.
4 贝叶斯优化结果
根据敏感性分析结果,选取各层开窗宽度、开窗间隔、中庭交界面开口面积及中庭天窗开口面积为贝叶斯优化的决策变量. 因贝叶斯优化为单目标优化算法,故目标函数设定为4项热压通风评价指标的加权和,温度及不均匀度等指标应取负,并对评价指标做无量纲化处理,即利用既有敏感性分析的样本值对各评价指标进行标准化,具体目标函数为
f=v-βv-T-βT
(6)
式中,v为平均风速(m/s);βv为风速不均匀度;T为平均温度(K);βT为温度不均匀度.
以高斯过程为概率代理模型,采用EI为采集函数,设置优化的迭代次数为50次,优化过程使用10核计算机,计算时间约4 d,根据贝叶斯优化时目标函数值的变化情况,可以判断收敛情况. 由图14中趋势线可知,该算法在前10次迭代时目标函数值上升迅速,在经30次之后缓慢上升,方差逐渐缩小,表明算法接近收敛.
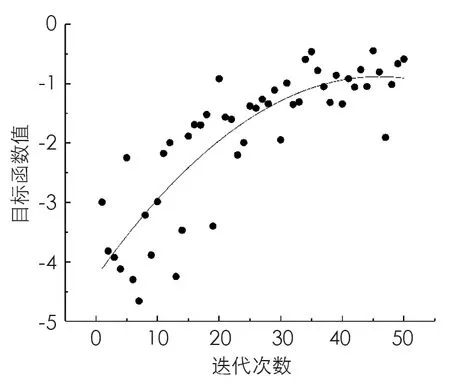
图14 贝叶斯优化过程的目标函数值
取迭代次数40次后且目标函数值大于-1.5的样本作为收敛后结果值进行评估,结果显示平均风速在0.36 m/s左右波动,风速不均匀度在0.2左右波动,平均温度在295 K左右波动,温度不均匀度在1.1 K左右波动,表明该算法能在参数空间内进行迭代以获得最佳的参数组合. 优化后的参数取值情况如图15所示,结果显示参数组合方案在开窗面积300 m2、交界面开口面积1 400 m2、天窗开口面积150 m2左右浮动时具有良好的通风性能. 对于8层建筑而言,中和面一般出现在4~5层之间,进一步分析各楼层开窗面积(图16)可知,位于中和面以下的各层开窗面积从40 m2到50 m2逐渐递增,而高于中和面的各层开窗面积则从20 m2到40 m2逐渐递增,同时观察外窗开口面积与中庭交界面开口面积的比值(图17)可知,中和面以下各层开窗面积与交界面开口面积的比值在0.2到0.3之间递增,中和面以上除顶层之外的各层则稳定在0.1至0.2之间,而顶层则在0.2至0.3之间.
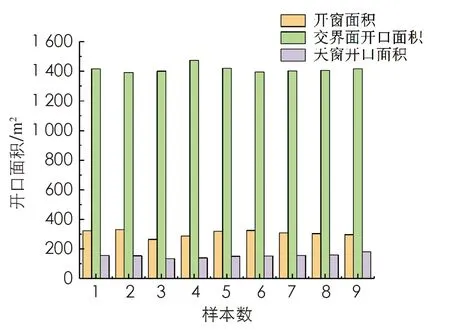
图15 优化结果的参数值

图16 各层开窗面积
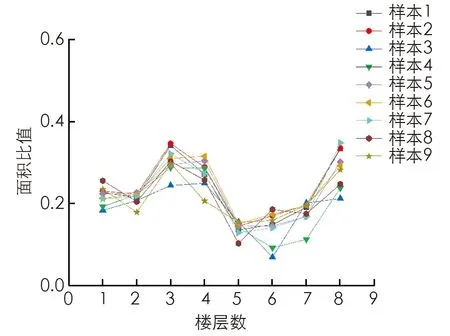
图17 外窗开口与中庭交界面开口面积比值
5 结 论
本研究选取4个指标构建目标函数对核心式中庭热压通风性能进行定量的评估,并结合参数化建模、CFD数值模拟、敏感性分析及贝叶斯优化对目标函数开展研究得到以下结论:
1)偏相关系数法和基于TGP的Sobol法的分析结果吻合较好. 中庭面积占比、开窗面积、交界面开口面积、天窗开口面积为设计敏感参数,天窗开口距顶层高度、建筑与中庭的纵横比为非敏感参数. 开窗面积、交界面开口面积及天窗开口面积之间相互作用明显,设计过程中应重点关注三者的组合情况.
2)针对本研究所示建筑,利用贝叶斯优化获得设计参数的最佳取值组合为开窗面积300 m2、交界面开口面积1 200 m2、天窗开口面积150 m2;同时对各层开窗面积与交界面开口面积的相互作用进行了探究,结果显示中和面以下各层开窗面积应大于上层开窗面积,开窗面积与交界面开口面积比值应在0.2左右.
3)基于参数化建模、CFD数值模拟、贝叶斯优化开发的计算机辅助设计工具,对各参数组合开展迭代优化,结果显示,仅需40步迭代即可获得较优的参数组合,可以应用于方案阶段的参数寻优过程.
上述基于敏感性分析筛选出的关键设计参数,以及通过贝叶斯优化探寻的最佳参数组合,可为核心式中庭建筑方案几何形态的设计提供定量的数据支持,需要强调的是以上结论仅是针对于满足模型构建的各种参数及假设下的理论值,实际方案阶段还应根据建筑形式、功能等方面进行权衡.

