基于点包容性检测的工程船越界检测算法 *
潘 伟,谢新连,李 猛
(大连海事大学 综合运输研究所,辽宁 大连116026)
0 引 言
随着海运事业的发展,人工航道逐渐增多,受自然因素的影响[1],人工航道的水深不能长久满足通航要求,致使一部分挖泥船定期在航道中进行疏浚作业[2]。在长江沿江地区经济高速发展的背景下,长江入海口航道船舶十分密集[3],加剧了通航船舶与疏浚工程船的碰撞危险,相关管理部门颁布了相应的航道管理办法来保证航道的正常通航秩序[4]。针对从事疏浚的工程船与航行船舶之间的冲突问题,在通航密度大的时间段内,疏浚工程船需让出主航道,使航行船舶能够根据管理部门安排有序通过。通过对工程船事故的调查发现,存在部分工程船为尽快完成施工要求,在交通管制时段内违规作业,造成险情甚至严重的碰撞事故。为了减少该类险情的发生,在交通管制区域进行实时监控,当有工程船违规进入交通管制区域时,会立刻被监控中心识别,如果及时对其发出警告,有极大可能在构成险情前使其退出交通管制区域。为实现工程船实时监控,检测工程船船位与交通管制区域的包含关系成为了核心问题。
在海事安全领域,对于船舶越界研究相对较少。但如果将船抽象为点,区域抽象为多边形,那么问题则转化为多边形的点包容性检测问题,该问题早在上个世纪便开始研究。早期学者主要针对多边形、多面体、流体等形式进行包容性检测的可行性进行了研究[5-7]。后期逐渐发展为优化包容性检测的效率以及适用范围,提出了“密切边”等新理论来提升包容性检测效率[8-9]。此外还有学者通过对原始的多边形、多面体等进行分解、排序来提升包容性检测的效率[10-14]。为了充分利用现有软件的运行效率,数据库管理系统提供的优化查询机制也被用来计算包容性检测问题[15]。
综上,点包容性测试算法通过不断优化,已能满足一定实际需求,可将点包容性检测算法应用于交通管制区域内工程船的实时监控。首先对交通管制区域边界和船位进行数学建模,为保证船位精度,采用雷达数据和AIS数据融合后的船位信息,并将船位误差转化到多边形边界中,将问题转化为多边形的点包容性检测问题;再结合水上交通实时监控对运算效率的需要,通过旋转区域模型以及射线法判定条件对射线法进一步优化,以提高求解数学模型的运算效率。
1 数学建模
检测工程船与交通管制区域存在包含关系,需要对工程船船位与交通管制区域进行数学建模,通过模型求解来判断工程船是否在交通管制区域内。
1.1 船位信息
船舶航行信息的融合是航海领域的热门研究方向,融合后的船舶航行数据兼具雷达与AIS数据的优点,使获得的船位信息更加可靠。船位误差δ是不能够被完全消除的,当获取的船位为点P时,则船舶的真实船位在以点P为中心,最大误差δmax为半径的圆形区域中,如图1。
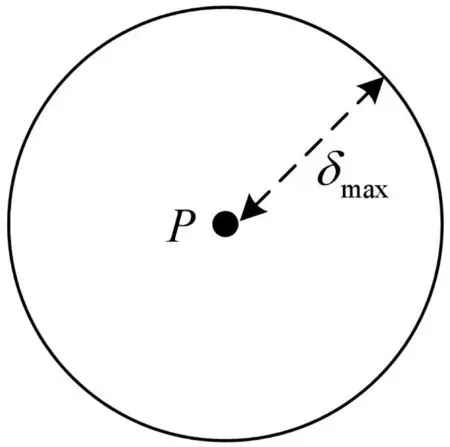
图1 真实船位可能存在的区域Fig. 1 The area where the true ship may exist
1.2 交通管制区域边界
根据墨卡托投影原理,投影后的海图从赤道向两极存在纬度渐长率,当基准纬度采用0°时,转化公式为:
(1)
式中:R为地球半径;(λ,φ)为弧度制表示的经纬度坐标;(x,y)为转化后的均匀直角坐标系坐标;e为第一偏心率。
通过式(1)将海图上确定航道边界的点和船位坐标从经纬度坐标转化为均匀直角坐标,进行点包容性检测。


图2 采用外切直线段简化弧形边界Fig. 2 Simplify the arc boundary with tangent lines
以矩形交通管制区域为例,将区域与船位进行数学建模后如图3(a),交通管制区域为矩形A1B1C1D1,真实船位在以点P为中心,δmax为半径的圆形区域中。若以此模型进行检测,是多边形的多边形包容性检测问题,检测方法比多边形的点包容性检测问题复杂。为降低算法复杂度,需将模型从多边形的多边形包容性检测问题,转化为多边形的点包容性检测问题。需将船位误差转化到区域范围误差中,转化后如图3(b)。

图3 修正前后的船位与交通管制区域Fig. 3 Ship position and traffic control area before and aftercorrection
图3(b)中,将原船位误差半径δmax附加到区域范围中,得到新的区域范围为圆角矩形A2B2C2D2,船位则直接采用点P表示。
笔者认为转化后的区域A2B2C2D2具有如下性质:利用转化后的区域A2B2C2D2进行点的多边形包容性检测时,当圆心点不在区域A2B2C2D2内,可断定原圆形区域内的任何一点均不在原矩形区域A1B1C1D1内。
对该性质进行证明(以点在多边形上侧为例):设以点P(x0,y0)为圆心,δmax为半径的圆形区域,与多边形A1B1C1D1的上侧边界无交点,与圆形区域距离最近的边界直线l0如式(2):
l0:y=ax+b
(2)
边界直线l0在附加误差半径δmax后得到修正的边界直线l,如式(3):
(3)
式中:α为该边界直线与x轴夹角。
点P(如图3)在直线l上侧,将点P的坐标带入式(3),点P位置有:
(4)
由于a=tanα,有:
(5)
a(x0+sinα×δmax)+b-(y0-cosα×δmax)<0
(6)
点P1(x0+sinα×δmax,y0-cosα×δmax)为原圆形区域下半边界距边界直线l0最近的点,且在直线l0上侧。结合P(x0,y0)在多边形A1B1C1D1上侧(图3)可知,原圆形区域内任何一点均在多边形A1B1C1D1上侧。同理可证点在多边形下侧的情形。
在实际计算过程中发现,圆角矩形的形式增加了计算复杂程度,不利于提高检验效率,因此对圆角矩形进行进一步简化,采用矩形形式进行检测,如图3(c)。从警报范围来看,简化后矩形区域包含圆角矩形区域,对于增补的4个角的面积,从理论上看会造成误报警,但其面积占整体区域比例小,且能大幅提高算法效率,可认为增补具有意义。
综上,转化后的数学模型为多边形的点包容性问题,求解运算复杂程度大幅降低。
2 算法优化
采用射线法求解笔者建立的模型。射线法的基本原理为:若要判断点P是否包含在多边形中,需从点P引出一条射线,射线与多边形边界的交点个数为奇数则点P在多边形内,交点个数为偶数则点P在多边形外,射线方向不影响算法检测结果。在实际运算中,发现射线法的检测时间会随船舶数量和交通管制区域边界顶点数量增多明显增长,无法满足实时监测需求,需对射线法进行优化。
2.1 多边形分区优化与射线方向设置
为提升求解速度,射线法在求解过程中普遍会设定射线方向。采用垂直于坐标轴的射线(简称垂向射线),当确定点的横坐标在多边形各个边界表达式的定义域外时,可判定点在多边形外。在判断点所在的子区域时,垂向射线法可以降低运算维度。
假设某区域如图4,进行建模后获得多边形Q1Q2Q3Q4Q5Q6Q7Q8Q9Q10Q11,各边的函数表达式集合为{Fi|i=1,2,…,11},存在6个需要检测的点为{P1,P2,P3,P4,P5,P6}。
高校图书馆员牢固树立“互联网+”思维,实现图书馆服务创新,将图书馆建设成汇聚优质资源服务的网络平台、教学资源可持续建设和运营平台,服务于高校师生的发展,以实际行动积极推动图书管理信息化建设。
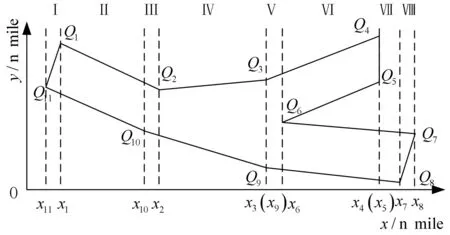
图4 根据x值将区域分段Fig. 4 Segment the region according to the x value
获取多边形各顶点的横坐标值为集合{x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11},将顶点的x坐标按数值升序排序并获得一个序列x11,x1,x10,x2,x3,x9,x6,x4,x5,x7,x8。根据实际情况,工程船在交通管制区域的边界上同样具有碰撞危险,因此区域的x值的取值范围为[x11,x8]。当检验点P的横坐标不在[x11,x8]中,则立刻可以判定点P不在多边形区域内。将序列去重后得:x11,x1,x10,x2,x3,x6,x4,x7,x8,区域[x11,x8]被分为8个子区域(图4),虚线将多边形分为8个区段,采用罗马数字为区段编号,各区段的x坐标范围为{DⅠ,DⅡ,…,DⅧ}。

图5 平行边界与辅助线示意Fig. 5 Schematic diagram of parallel boundary and auxiliary line
根据通航水域警戒区与监控区域边界设置的实际情况,监控区域中存在一定量的平行元素(包括边界和与边界平行的辅助连线),如图5。图5中虚线Q2Q10、Q6Q9、Q3Q9为辅助线。边界Q1Q11、Q7Q8与辅助线Q2Q10、Q6Q9平行,边界Q4Q5与辅助线Q3Q9平行。
结合分区原则,对区域绕指定点进行二维旋转。求得区域每个顶点与其他顶点的连线斜率,获得斜率集合Sl。求集合众数Ml,其对应的直线与y轴之间的锐夹角即为旋转角β。如图6,将原区域绕点G旋转度,获得新的区域位置,该区域由8个区段减少到6个区段。
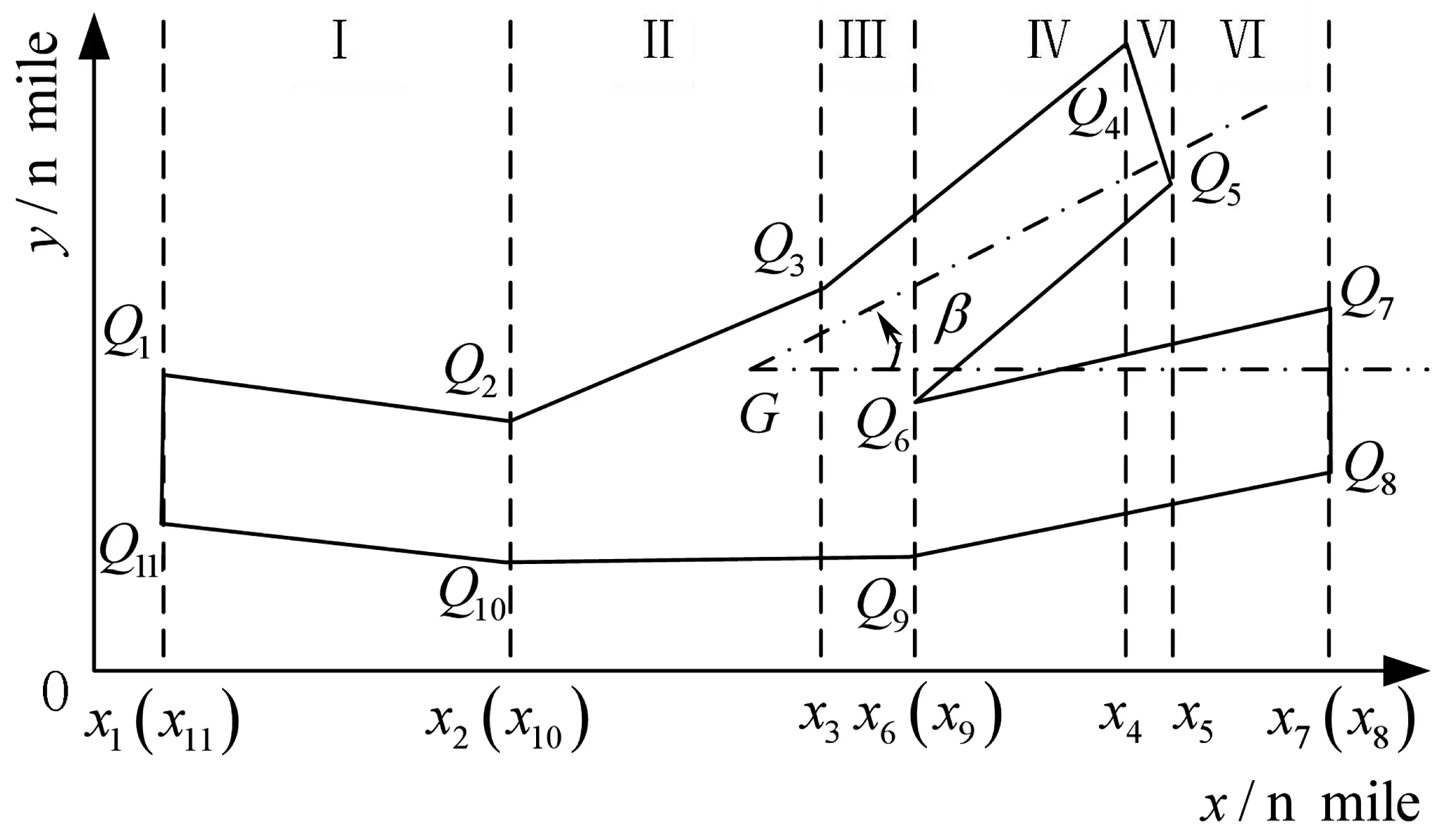
图6 区域旋转示意Fig. 6 Schematic diagram of regional rotation
2.2 包容性检测判定条件设置
基于船舶航行以及监控实际需求,考虑船舶在边界上同样存在碰撞风险,需要对射线法的判定条件进行进一步优化。以在区段Ⅵ检测为例(图7),线段Q6Q7在区段Ⅵ中的部分为Q′6Q7,线段Q8Q9在区段Ⅵ中的部分为Q8Q′9,点P1、P2、P3、P4为4个检测点。点P1引出向上的垂向射线与边界有一个交点,点P3引出向上的垂向射线与边界有0个交点,均符合射线法的判断准则。点P2、P4情况较为复杂,由点P2引出向上的垂向射线穿过多边形两条边界Q′6Q7、Q8Q′9及一个顶点Q5。经过顶点Q5的情况较为特殊,结合各区段采用闭区间的要求,Q5既属于区段Ⅴ,又属于区段Ⅵ,为保持每区段边界的个数为偶数,交点为顶点Q5的类似情况不计入任何区段的交点个数中,设置判定条件:①当需要判定的点所引出的射线经过某边界点,且该边界点不为穿越该区段的边界点时,该点不计入射线穿越边界个数;②当需要判定的点所引出的射线与边界共线时,统计射线穿过共线边界的端点个数即可;③若所需判定的点为垂向线段端点(即多边形的顶点),判定其在多边形内。

图7 点与特殊边界的关系Fig. 7 The relationship between points and special boundaries
设定判定条件后点P2引出的垂向射线与多边形的交点个数为2个,判定点P2在多边形外;点P4引出的垂向射线与多边形交点个数为1个,判定点P4在多边形内,与实际相符且符合射线法的判断准则。
通过设置判定条件,确定了每一个区段内边界的数量均为偶数。根据射线法的判断准则,统计射线穿过边界的次数。当射线起点的x值在第i区段的区间范围Di中时,仅需要判断射线起点(船位)与两个边界的关系,以两条边界为例,如式(7):
Ti(x,y)=aix+bi-y
(7)
式中:Ti(x,y)为点与直线的关系判别函数;i=1,2;ai与bi为直线参数,i=1,2。
利用T(x,y)判断点P(xP,yp)与边界关系并满足:
(8)
式中:xp,yp为P点坐标值。
若点在两条边界直线的同一侧,表示点在多边形外,其他情况均表示点在多边形内(点在多边形边界上算作在多边形内),则可归纳出:
(9)
将该结论推广到一个区段内存在两条以上边界的情况。区段内边界数量为偶数k,则判定表达式为:
(10)
2.3 算法流程
将优化部分整合,完成优化射线法的整体设计,包括3大部分:获得数据、区域模型处理、算法检验。算法流程如图8。
3 算例分析
为了检验优化后的射线法(下简称优化射线法)有效性,选取吴淞口附近的一个警戒区进行算例分析,如图9。
为了体现优化射线法的优越性,采用角度和法、传统射线法、垂向射线法、优化射线法共4种算法同时对相同环境数据进行检验。前3种算法计算流程见文献[20],传统射线法采用斜率为1的射线进行算法检验;垂向射线法采用垂直于x轴并向x轴正方向延长的射线进行检验。4种算法均采用C++ 语言编写实现,运行主机CPU为i7 5700HQ,内存为32 GB,操作系统为Windows 7。
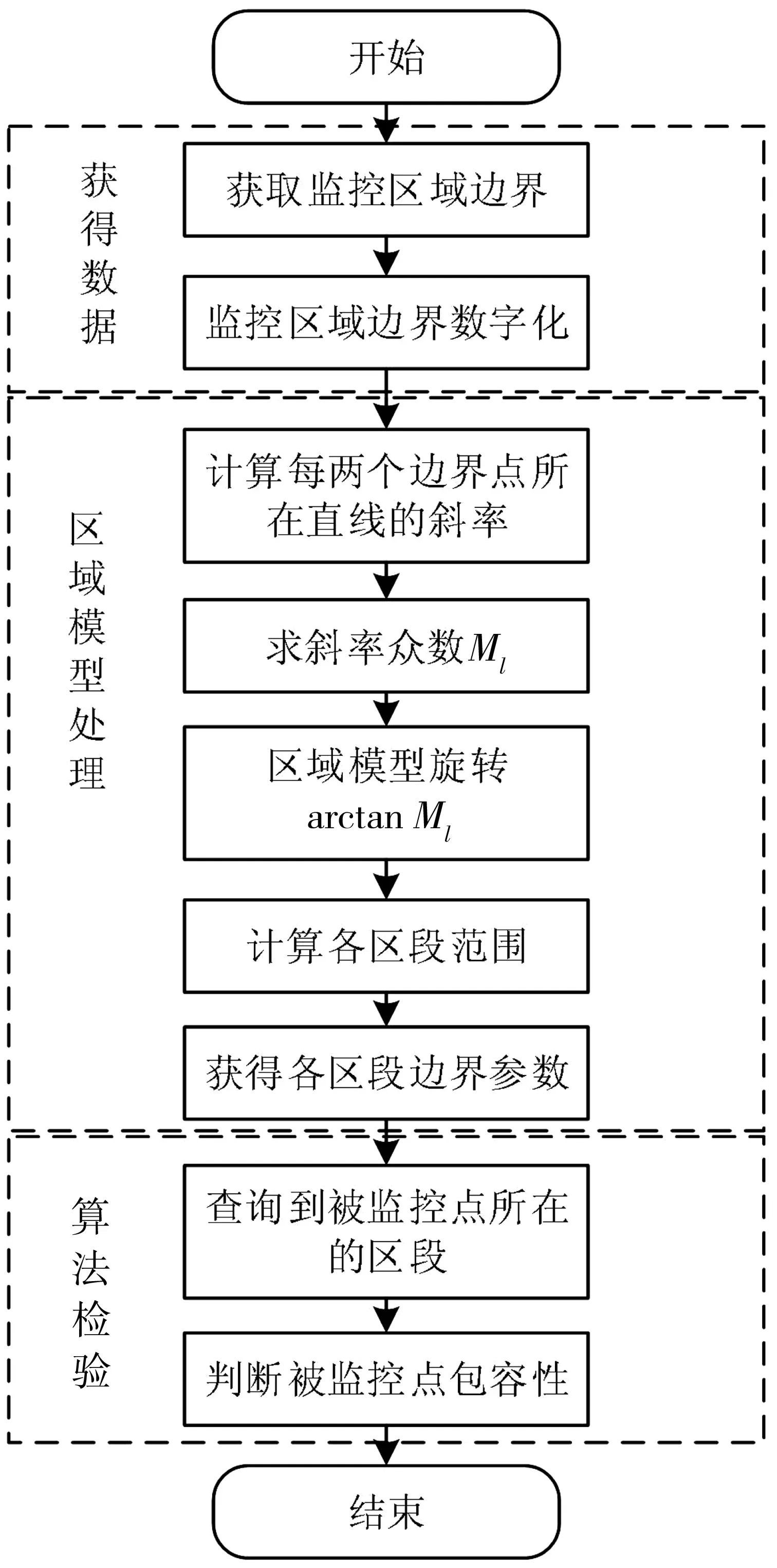
图8 算法流程Fig. 8 Algorithm flow chart
将吴淞口水域附近选定的监控区域进行数字化,获得边界坐标,并选择大于边界的范围作为实验区域。为方便获取算法运行时间,在实验区域内随机生成10万个点,为能够有效比较4种算法的运行效率,用4种算法检验同一组随机点,进行100次实验,结果如图10。

图9 吴淞口警戒区及航道Fig. 9 Precautionary area and channel of Wusongkou
对图10进行分析,可以得到以下结论:
1)角度和法、传统射线法、垂向射线法、优化射线法4种算法均具有良好的稳定性,在实验环境一定的情况下,射线法相比于角度和法更加稳定。
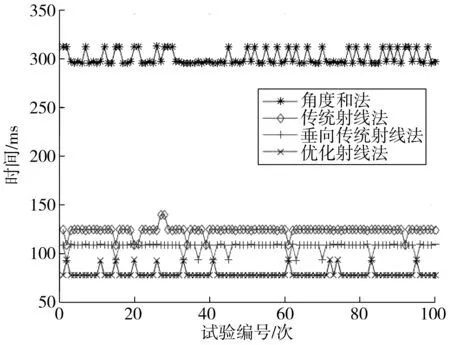
图10 4种算法运行时间比较Fig. 10 Comparison of running time of four kinds of algorithms
2)优化射线法相比于垂向传统射线法运行效率提升约25.68%;优化射线法相比于传统射线法运行效率提升约35.51%。
3)射线法在优化过程中,运行效率有大幅提升,其稳定性与传统射线法、垂向传统射线法相近,可通过并发方式进一步提高算法稳定性。
4 结 论
根据对工程船实际监控需要,采用点包容性测试算法来解决通航水域施工船越界检测问题。对算法进行应用时发现,不同包容性检测算法的应用范围存在较大的差异,导致不同算法解决同样问题时运算效率不同。针对需要监控的通航水域特点,创新采用了多边形分区与射线方向相结合的优化方法,使其在解决工程船越界检测问题时具有更高的运算效率,并获得以下结论:
1)实验结果表明优化射线法在运算效率方面有了较大幅度的提升,与固定斜率的射线法(斜率不为0)相比运行效率提升约35.51%,与垂直设置射线的射线法相比运行效率提升约25.68%。并且在处理复杂多边形区域时能保持高效率运算。
2)从实际应用角度来看,在无法降低获取船位报文与解码时间的情况下,大幅提高检测算法的运算效率是保证检测系统在规定时间内完成检测任务的有效方式。
3)改进后的算法可以推广到不同的监控环境中,例如禁航区的船舶监控、锚地船舶监控、施工水域船舶监控等。尤其是针对通航密集的水域进行船舶检测,改进后算法的高效性和稳定性可以帮助监控系统在规定时间内完成船位越界检测任务。

