小学数学教育专业师范生专业信念的调查研究
张乐乐
(伊犁师范大学 教育科学学院,新疆 伊宁 835000)
一、问题提出
为全面提高师范生培养质量,建设高素质专业化的教师队伍,教育部颁发《教师教育课程标准 (试行) 》(2011)明确了师范生教师教育课程的基本要求,其中教育信念与责任成为师范生教师教育的首要课程目标,这为师范生培养指明了方向。信念是具有强烈个体意义的、带有情感性的个体知识[1],数学教师的专业信念是其教育信念的关键部分,是数学教师持有的与数学、数学的教与学等有关的思想和观点[2],涉及数学的本质信念、学习信念、教学信念等。教师信念是教育教学改革和教学质量提升的首要条件,也是教师专业发展的内在动因。已有研究表明使教师成为优秀教师的,不是他们的知识或方法,而是教师对学生、自己、他们的目的、意图和教学任务所持的信念[3]。
2020年8月《教育部等六部门关于加强新时代乡村教师队伍建设的意见》指出,各地要加强面向乡村学校的师范生委托培养院校建设,促进师范生职业素养提升。基础教育阶段的教师素养以基础素养、专业素养、综合型素养为核心要素[4],专业信念是专业素养的“软件”,因管理着教师专业素养的硬件而起着重要的作用。职前教师的数学信念主要在小学和初中、高中时期形成,并在大学接受教师教育的过程中产生变化和确立[5],未来的教师对数学、学生以及数学学习的信念影响到他们对教学法知识的获取和教育实践[6],甚至阻碍师范生健康全面的专业发展以及由学生向教师角色的顺利转变[7]。所以教师信念的培养无疑是师范生教师教育中最重要的内容[8]。虽然现有关于教师信念的研究兼顾了在职教师群体和师范生群体,但农村地区和民族地区教师教育信念的研究被严重边缘化[9],少数民族教师信念研究更是处于边缘地带[10]。因此,本研究欲考察民族地区师范类院校小学教育师范生专业信念的现状及发展特点,为师范生教师教育及未来职后数学教师教育培养提供方向和参考。
二、研究设计
(一)被试选择
调查者是民族地区某地方师范类院校教育学院小学教育(理科方向)专业的本科学生,涉及2017级、2018级、2019级、2020级四个年级学生,2017级的问卷调查是在他们最后一个学期离校前实施的。抽样方法为整群取样,总计发放问卷共440份,回收有效问卷432份,有效率98%。调查中少数民族师范生285名,占65.97%,女生占总体87.5%,体现出民族地区小学教育师范生构成女性居多、少数民族教师比例较大的特征,具体信息如下表1所示。
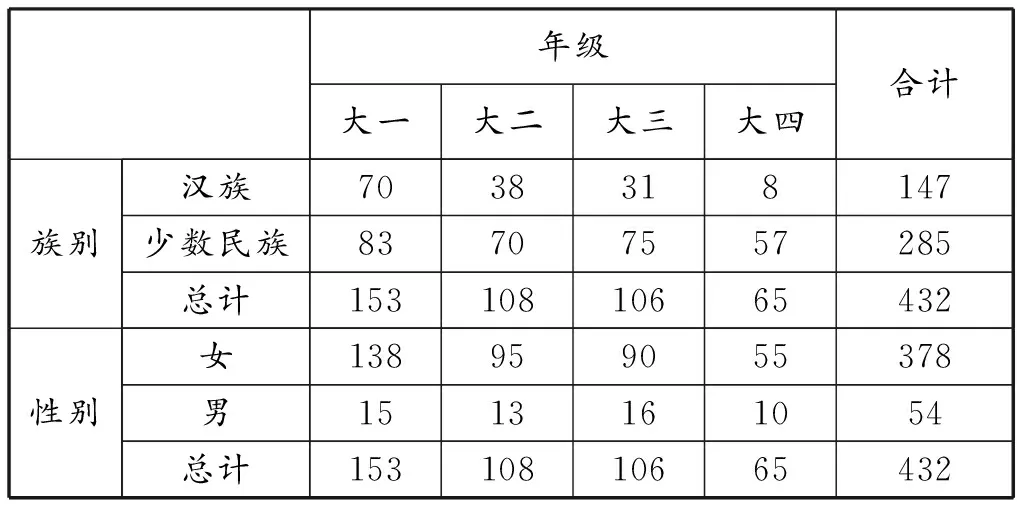
表1 调查对象基本信息
(二)工具
TEDS-M(Teacher Education and Development Study in Mathematics),即教师教育和发展研究—数学,是世界上首个中小学职前数学教师教育项目大规模国际比较研究项目。
TEDS-M专门针对小学和初中的职前数学教师构建了以专业知识和专业信念两大核心成分为数学教师专业素养的框架。TEDS-M认为数学教师专业信念由对数学本质的信念、对数学学习的信念、对数学成就的信念、对数学教学准备的信念、对教师教育效用的信念五个部分构成。研究提取其框架以数学教师专业信念为一级指标, 以数学本质的信念、数学学习的信念、数学成就的信念为二级指标构建调查问卷,共翻译调整34个题项,采用Likert自评六级量表形式计分,从 非常不赞同、不赞同、稍微不赞同、稍微赞同、赞同、非常赞同分别记为1-6 分,得分越高表示越认同该观点,通过学生自评的方式来了解其宣称的专业信念。为检验该量表对于国内职前教师的适用性,采用内部一致性Cronbach α系数对34个题目进行内部一致性信度检验,计算出总Cronbachs’α系数为0.877,表明很符合一般量表推广的要求。
(三)数据处理与统计方法
数据处理:TEDS-M认为第1到第2个回答表示不赞同,第5和第6个回答表示赞同,使用SPSS对所有数据进行重新编码,最终数据:1代表不同意、2代表中立、3代表同意。对统计到的数据使用SPSS进行描述性统计和推断性统计得出师范生专业信念的现状及特点。
三、研究过程与结果
(一)小学教育师范生专业信念各维度基本情况
分别统计大一至大三、大四师范生各维度均值如表2所示。总体上看,全体师范生数学本质信念两个维度均值均大于2.5,且问题解决主义数学观得分高于柏拉图主义数学观。数学学习信念中信息加工主义学习观得分均大于2(中立),建构主义学习观大于2.5,建构主义学习观得分高于信息加工主义学习观。数学成就信念得分小于2(中立),倾向于不赞同先天的数学信念观。对比发现,大四师范生在各信念上的认同取向上与其他年级师范生一致,且认同度(得分)都高于其他年级。各维度标准差中,数学成就信念标准差(0.53)最大。
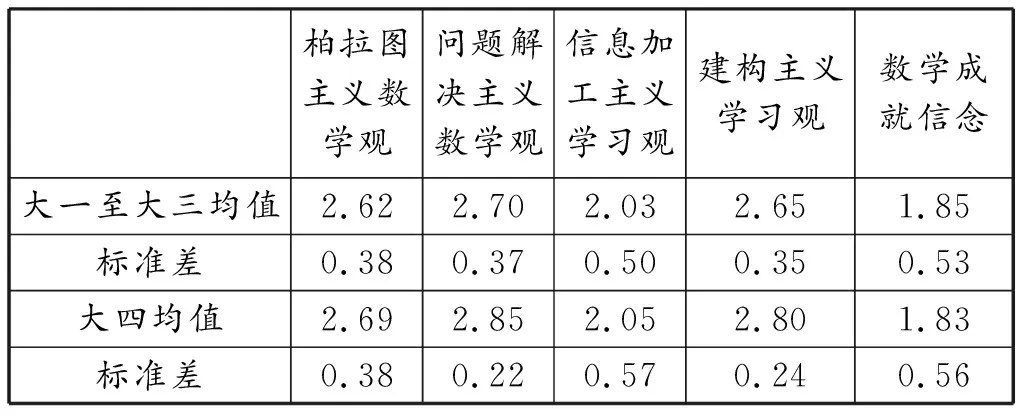
表2 数学专业信念各维度均值
(二)民族与专业信念的关系
经检验,发现师范生的专业信念在性别和有无家教经验两个变量上不存在显著性差异。为了进一步了解师范生的专业信念是否存在民族差异,以民族(汉族和少数民族)为自变量,以五个维度为因变量,进行独立样本 t 检验,结果见表 3。
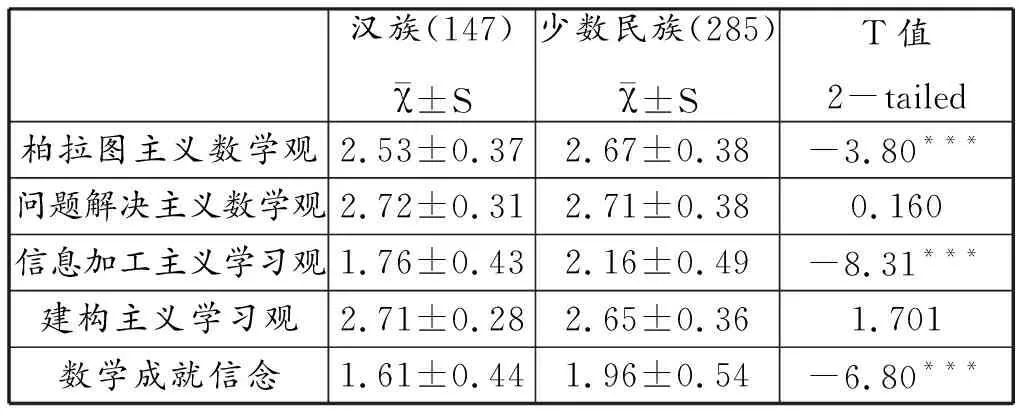
表3 不同民族在数学专业信念各维度上的差异
从表3的数据信息中可以看出,汉族与少数民族师范生在柏拉图主义数学观、信息加工主义数学观、数学成就信念上均存在极其显著性别差异(P<0.001)。在数学的本质信念上,少数民族师范生柏拉图主义数学观(2.67±0.38)得分显著高于汉族师范生(2.53±0.37);数学学习信念上,少数民族(2.16±0.49)师范生信息加工主义学习观得分显著高于汉族(1.76±0.43);数学成就信念方面,少数民族师范生(1.96±0.54>1.61±0.44)得分更高。
(三)年级与专业信念的关系
为反映不同年级师范生专业信念的发展特点,以年级为自变量,以专业信念5个维度为因变量做单因素方差分析,并对其进行事后检验,得到的数据表使用字母标记法标记在图中(同一指标不同字母表示差异显著),结果见图1。
单因素方差分析发现:年级分类的主效应显著,不同年级的师范生在柏拉图主义数学观(F=3.64,P=0.013)、问题解决主义数学观(F=6.67,P=0.000)、 信息加工主义学习观(F=11.60,P=0.000)、建构主义学习观(F=4.82,P=0.003)、数学成就信念(F=3.02,P=0.029)均存在显著差异。据图1可知,大一学生在问题解决主义数学观上得分显著低于其他年级,大二学生在柏拉图主义数学观上得分显著性低于其他年级,大四学生在建构主义学习观得分显著高于其他年级。
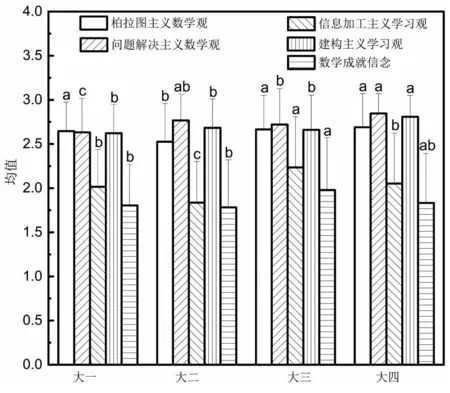
图1 数学专业信念各维度在年级上的差异
(四)年级对数学兴趣与专业信念的关系
以年级为自变量,以对数学感兴趣程度为因变量做单因素方差分析,发现大四的数学兴趣与其他年级的师范生存在显著性差异,其对数学的感兴趣程度显著高于其他年级(P<0.05)。以数学兴趣为自变量,以专业信念各维度为因变量做单因素方差分析,并对其进行事后检验,结果见表4。

表4 数学专业信念在数学兴趣差异上的事后检验
单因素方差分析发现:除信息加工主义学习观(F=1.10,P=0.333)维度以外,数学兴趣在柏拉图主义数学观(F=12.18,P=0.000)、问题解决主义数学观(F=28.29,P=0.000)、 建构主义学习观(F=7.27,P=0.001)、数学成就信念(F=7.02,P=0.001)均存在显著性的差异。事后检验发现:对数学不同兴趣程度组在问题解决主义数学观得分差异均有统计学意义 (P<0.05),且对数学越感兴趣的师范生问题主义数学观得分越高,对数学不同兴趣程度组在数学成就信念得分上存在显著性差异(P<0.05),且对数学越感兴趣的师范生数学成就信念得分越低。
(五)小学教育师范生专业信念各维度的相关关系
为了更加深刻地了解专业信念各维度之间的关系,对各维度之间做相关分析,结果见表5,发现:柏拉图主义数学观与其他专业信念维度均存在极其显著差异(P<0.01),建构主义学习观与问题解决主义数学观存在极其显著正相关(P<0.01),但与数学成就信念相关性不显著,数学成就信念与信息加工主义学习观存在极其显著正相关(P<0.01),与问题解决主义数学观、建构主义学习观不相关(P>0.05)。

表5 小学教育师范生专业信念各维度的相关矩阵
四、讨论
(一)小学教育师范生专业信念总体水平
在数学本质信念上,师范生具有柏拉图主义数学观,但又具有问题解决主义的数学观,这种既有绝对主义的信念又有谬误主义的数学信念,凸显出对数学本质信念的综合性和矛盾性,体现出人们对于数学的本质属性理解的发展却是徘徊不前的。数学学习信念上,师范生更加认同基于谬误主义数学观建立起来的建构主义学习观,即以学生为中心的数学学习观,认为学生通过自主探索也能学好数学。数学成就信念上,师范生更加赞同数学的成就很大程度上取决于自身后天努力的学习,但对于成就先天论还是后天论的看法不统一分歧较大。
(二)不同民族师范生专业信念的差异
相比起汉族师范生,少数民族师范生更认同柏拉图主义数学观、信息加工主义学习观、数学成就信念的天生论,表明少数民族师范生在数学本质信念、学习信念、数学成就信念方面均存在落后的信念,与王书臣“少数民族高校新生的数学观普遍较片面、模糊,需要帮助学生建立积极的、多元的、动态的数学观”[11]的研究观点一致。数学的抽象特征,在汉语言不通,理解不明的情况下,少数民族学生数学学习上容易形成机械训练的学习方法,解题训练变成获得高分的单一来源,造成对数学片面的认识。由于高校少数民族师范生普遍在数学学业成绩上不理想,缺少在数学上获得的成就感,丧失学习的兴趣与自信心,很难建立起后天努力能够获得数学成就的信念。
(三)不同年级师范生专业信念的差异
研究结果显示,问题解决主义数学观上大一得分显著低于其他年级,柏拉图主义数学观上大二得分显著低于其他年级,建构主义学习观上大四得分显著高于其他年级。大一学生对数学的认识受中学数学学习影响较大,经常性的数学训练与考试,造成了对数学静态的、绝对主义的、严谨性的、精确性的认识,形成了绝对主义数学观,大二师范生开始接触“数学史选讲”“小学数学课程与教学论”等专业课程,通过对数学文化、数学学科的了解,对数学本质的认识向动态的、辩证的、发展的、建构的人文主义与科学主义相结合的数学观的转变[12]。大四师范生有支教实习的特殊经历,期间通过教学实践与反思,结合新课程理念的影响,教学上更加以学生为中心,提倡学生主动探索与思考的建构主义学习观。
(四)不同年级对数学不同兴趣状态师范生专业信念的差异
大四学生对数学的兴趣显著性高于其他年级,大四师范生经历过支教的教学实践,有更高的专业认同感[13],且有通过数学的趣味性来调动课堂上学生学习的兴趣和动机的教学思考与尝试,也可能由于具有良好的数学本质信念影响本人对数学的情感态度,使本人对数学的感兴趣程度显著性高于其他年级。越是认为数学有趣的师范生,越是认为数学是一个不断创造和发现的过程,数学问题的解决方法具有开放性,赞同问题解决主义的数学观,越是认为数学有趣的师范生,越是认同数学获得的成就不是天生的,而是靠后天努力,具有后天的数学信念。大四师范生相对于其他年级具有明显的问题解决主义数学观和后天的数学信念。
(五)小学教育师范生专业信念各维度的相关关系
学生问题解决主义数学观越强,建构主义学习观越强;信息加工主义的学习观越强,则数学成就的先天论信念越强。在一定程度上对数学本质的信念决定了对数学学习的信念,对数学学习的信念又决定了数学成就的信念,可见数学本质信念会对数学学习观和数学教学观产生很大影响[14]。除此之外,数学教师对数学的信念不仅会影响教师知觉与处理班级中信息与问题的方式,而且影响教学目标的形成以及教学任务的定义方式,甚至是教师的行为方式与教学效能感[15]。
五、结论及建议
总体上,师范生具有进步的数学专业信念,相对于汉族学生,少数民族师范生的数学专业信念相对落后,低年级师范生的数学专业信念受初高中学生时期学习及教师教学影响较大,经过四年师范教育,专业信念虽然有一定发展,但并没有发生颠覆性的转变。大四师范生作为职前教师,在数学本质信念、数学学习信念、成就信念维度上的认同取向与其他年级师范生保持一致,但大四师范生对数学的兴趣显著性高于其他年级,对问题解决主义数学观和建构主义数学观的认同、数学素养获得的后天论上得分均显著高于其他年级,说明大四师范生具有相对更进步的专业信念,但与其他低年级师范生一样在数学本质信念上仍未形成清晰的认识。介于数学本质信念对于其他专业信念的重大影响力,作为基础教育阶段数学教师的培养者,应当将转变学生绝对的、静态的、柏拉图主义数学观作为教学的重要任务,教学中除了增加学生对数学基础知识、基本技能、基本方法的掌握,还应增加学生对数学史知识的了解,引导学生从历史和文化的视角来审视数学的发展与变化。其次,师范生的支教经历对于其专业信念的影响显而易见,因此夯实师范生教育见习、实习环节,避免走马观花的形式化,保证师范生能接触到丰富而多样的教育机会和教学资源,感受到优秀课堂教学的魅力。同时指导教师及时组织提供机会,使学生进行有效的反思性、质疑性学习应是需要重视的重要环节,能起到帮助学生意识并反思自我专业信念的作用,是帮助学生纠正错误信念的良好机会。此外,少数民族师范生相对于汉族师范生具有相对落后的专业信念这一现实问题,需要教育者给予这一群体特殊关注,帮助他们提高数学学业成绩,改善学业评价的标准,提升其对数学学习的自我效能感和成就感,通过改变数学的成就信念推动对数学学习的建构主义认识,最终建立起问题解决主义数学观。大学期间,大学专业课教师关于学科专业信念不仅通过其课堂上宣称的方式传递,还通过其教学方法、策略、教学评价等实践方式被学生感知,高校教师自身建立知行一致的数学专业信念亦是学生信念的发展必要条件。

