基于新型混沌细胞神经网络的图像加密算法
马英杰,郑子怡,赵 耿,曾 萍
(北京电子科技学院,北京 100070)
1 引言
细胞神经网络(Cell Neural Network,CNN)是一种大规模的非线性模拟电路,它能实时并且高速并行的处理信号,规则的结构易于实现超大规模集成电路,是一种灵活有效的神经网络模型。细胞神经网络是非线性的,其复杂的动力学行为可以生成混沌信号,该混沌信号可以应用到加密中。研究表明,高维的细胞神经网络模型具有更加复杂的超混沌行为,相比一般的混沌行为来说具有更多的可控参数,同时具有实时性的特点,能够在混沌系统的基础上进一步提高系统的保密性、安全性和有效性,因此,对混沌细胞神经网络的加密算法研究具有十分重要的理论意义和工程实践价值。近年来,各个国家的研究者都提出了不同的基于细胞神经网络的加密算法,以满足信息保密要求。文献[1]分析了高维细胞神经网络的特点,设计了伪随机序列发生器,对图像进行置乱、横向和纵向的扩散。文献[2]采用六维CNN,引入无限折叠映射,提升了加密算法的复杂度。文献[3]应用CNN生成超混沌序列,以此作为AES加密算法的目标密钥,将明文图像的像素与目标密钥异或加密后得到密文图像。文献[4]提出一种基于CNN的图像加密新算法,以一个6维CNN产生的超混沌系统作为密钥源。文献[5]研究了Cheng等提出的基于自适应同步混沌细胞神经网络和统一混沌系统的非对称图像加密方案,证明了其方案不适合在图像安全加密中实际应用。文献[6]提出了基于细胞神经网络CNN 超混沌的特性结合一般形式的三次函数鲁棒映射和高维Lorenz系统对图像采取双扩散—置乱的加密操作。文献[7]以4阶 CNN 模型为基础,提出了一种新的超混沌细胞神经网络图像加密算法,使用不同初始状态和参数的复合混沌映射生成高阶混沌细胞神经网络的初始条件,以生成扩散阶段的密钥流。文献[8]提出了一种基于生物DNA序列运算和CNN的图像加密方法,该方法由比特替换、密钥流生成和扩散三个过程组成。
本文提出一种基于新型混沌细胞神经网络的图像加密算法,在选取密钥时,根据明文图像的像素值来确定,保证了算法对明文的敏感性,另外图像中每个像素点的密钥都不同,这在很大程度上提高了算法的复杂程度,增强了安全性。
2 混沌细胞神经网络模型
2.1 细胞神经网络模型
细胞神经网络的概念是1988年由Chua和Yang提出来的[9-10],是对人工神经网络模型的改进。CNN的基本单元为细胞,每个细胞都是一个非线性一阶电路,由一个线性电阻、一个线性电容和一些压控电流源组成,如图1所示。

图1 细胞神经网络单元电路图
图中uij是细胞的外界输入,xij是细胞的状态变量,yij是细胞的输出。细胞神经网络就是由多个这样的细胞单元连接组成的,细胞C(i,j)只和临近的细胞C(k,l)相连接,连接点为压控电流源Ixu和Ixy。确定相邻细胞是判断其是否处于细胞C(i,j)的邻域Nr内,Nr的定义如下
Nr={Cij:max(|k-i),
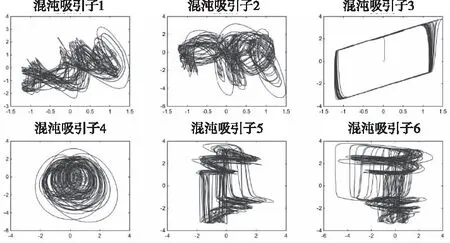
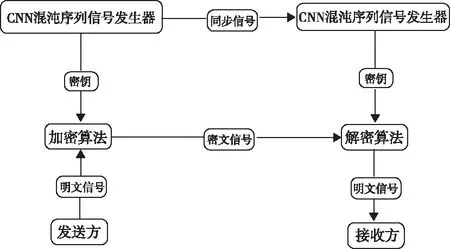
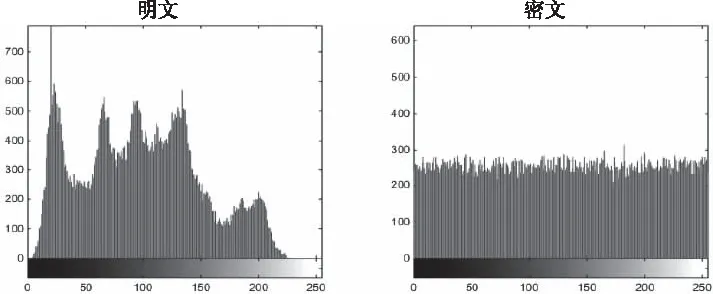
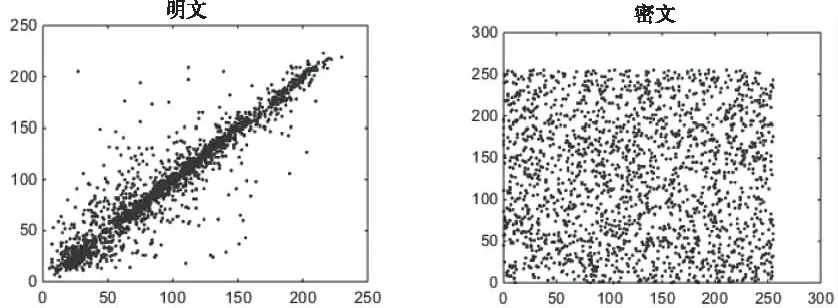
|l-j|≤1 (1) 由此可以写出细胞C(i,j)的状态方程: (2) 为了后续计算简便,引入简化版的推广CNN模型,那么无量纲的状态方程可以表示为 (3) (4) 其中aj是常数,f(xj)表示细胞的输出,G0和Gs表示连接细胞的输出值和状态变量的线性组合,Ij表示门限值。 基于符号函数,构造了一种新型混沌细胞神经网络,其无量纲状态方程为 (5) 新型细胞神经网络的混沌吸引子如图2所示,初始值取(0,0,0,1e-10)。 图2 新型CNN混沌吸引子 采用构造的新型混沌细胞神经网络生成混沌序列,基于混沌序列选取密钥对图像加密,解密过程是由相同的细胞神经网络模型生成相同的混沌序列,按照同样的规则得到密钥,就可以对图像进行解密,方案如图3所示。 图3 方案描述 加密算法的具体过程如下(假设图像大小为a×b×c): 1)产生混沌序列:由新型四阶混沌细胞神经网络生成四维混沌序列,将每一维混沌序列都进行相同的预处理,从第3216位开始截取a×b长度的序列,将截取序列中的每一位都扩大100倍,取整后再取绝对值,对256取余,最终得到一个字节的无符号整数。 2)选取密钥:明文图像中的像素点(i,j)与前一相邻像素点的像素值异或,将结果模4加1,处理成1—4范围内的整数,记为index,对于(i,j)位置的像素,取第index维序列中的第i×j个数据作为其加密密钥jiamikey,第index+1、index+2维序列中的第i×j个数据分别作为其置乱密钥zhiluankey1、zhiluankey2。 3)像素位置置乱:将像素点(i,j)和像素点(h,g)互换位置,如式(6)所示 (6) 其中n是取值从1到20的正整数,表示位置置乱的这部分算法迭代进行20次。 4)像素值替代:置乱后图像中的各像素点分别与其加密密钥异或处理,得到最终的密文图像。 解密具体过程如下(假设图像大小为a×b×c): 1)产生混沌序列:由同步的细胞神经网络混沌序列接收器产生相同的混沌序列,进行同样的预处理,截取a×b长度的序列,将每一位都扩大100倍,取整后取绝对值,然后对256取余,最终变成一个字节的无符号整数。 2)确定密钥:将接收到的文件中各像素值异或的结果逐个读取出来,记为index,取第index维序列中的第i×j个数据作为其加密密钥jiamiky,第index+1、index+2维序列中的第i×j个数据作为其置乱密钥zhiluankey1、zhiluankey2。 3)像素反替代:将密文图像各像素点分别与其加密密钥异或处理。 4)位置反置乱:将像素反替代后的图像进行位置反置乱,得到最终的解密图像,如式(7)所示 (7) 其中n是取值从20到1的正整数,表示位置反置乱的这部分算法反迭代进行20次。 直方图是一个二维的直角坐标图,横坐标表示不同像素值,纵坐标表示出现的频次,这样的一个直角坐标图标绘了图像中每个像素值的像素数,可以直观地看到图像整体像素值的分布情况。 对明文图像和密文图像分别求取直方图,如图4所示,可以看出在加密前图像的像素值分布不均匀,加密后图像的像素值均匀地分布在200—300之间,这表明加密算法的安全性较好,能够打破明文图像的特点,使密文图像的像素值分布均匀。 图4 直方图 相关性是指两个变量之间的关联程度,随机选取2000对相邻像素进行相关性分析,相关性如图5所示。 图5 相关性图 从图5可以看出,加密前的图像近似于一条斜率为1的直线,加密后的图像在一个固定的范围内均匀分布。这表明系统算法相邻像素之间的相关程度低,相互位置关系无序,性能好。 明文敏感性是指当明文图像有变化时,最后的加密结果也会不同。引入NPCR和UACI两个量来衡量明文敏感性,NPCR是指当明文图像有一个位置的像素值发生改变时,密文图像中像素值改变了的像素个数占总像素个数的比例,理想值是0.9961;UACI是指这两幅不同图像之间的平均强度差,理想值是0.3333。 将(8,46)位置的像素值变为0,计算NPCR的值为0.9960,UACI的值为0.3331。为了使测试结果更具有普遍性,再分别改变(4,23)、(2,12)位置的像素值为0,计算明文敏感性,结果如表2所示。可以看出,算法三次改变像素值后NPCR的计算结果都近似于0.9961,UACI近似于0.3333,这说明算法的明文敏感性较好,能根据不同的明文图像反馈不同的密文图像。 表1 不同像素值明文敏感性 密钥敏感性是指当初始密钥发生变化时,最后的解密结果也会不同。引入可以定量计算的数值来衡量密钥敏感性,计算当密钥改变一位时解密图像中像素值改变了的像素个数占总像素个数的比例,理想结果是0.9961。 算法原本的初始密钥是[0,0,0,1e-10],在测试中,改变密钥万分之一的程度,变为[0,0,1e-4,1e-10]后对密文进行解密,敏感性的计算值为0.9961。为了使测试结果更具有普遍性,再分别改变不同程度的初始密钥,将结果与文献[4]进行对比,如表2所示。可以看出,三次改变初始密钥后的计算结果都近似于0.9961,并且相较于两篇对比文献,本文提出算法的三次测试结果的平均值为0.996,整体来说更接近于理想值0.9961,说明算法的密钥敏感性较好,能根据不同的明文图像反馈不同的密文图像,能有效抵御穷举攻击,攻击者获得的密钥与正确密钥即使有很微小程度的差别也无法正确解密。 表2 密钥敏感性对比 本文提出了基于新型细胞神经网络的图像加密算法,能够有针对性地解决普通流密码不具有明文敏感性的问题,提出的算法根据明文图像的像素值来选取密钥,选取了四阶细胞神经网络生成四维混沌序列,按照一定的规则选取密钥。仿真结果表明,提出的算法能够有效抵御差分攻击,具有高度密钥敏感性,明文敏感性以及相邻像素间近似于零的相关性,保证了算法的安全性和可靠性。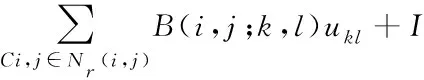
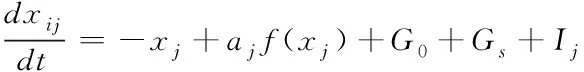
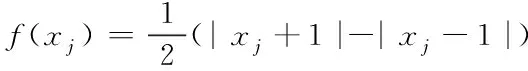
2.2 新型混沌细胞神经网络
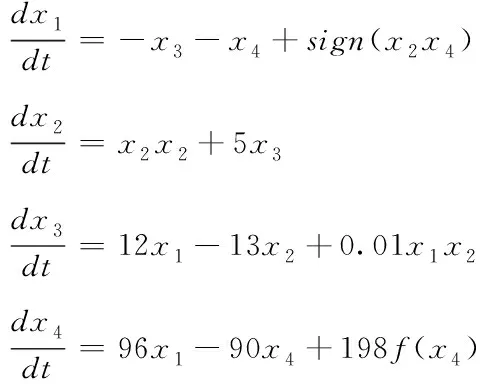
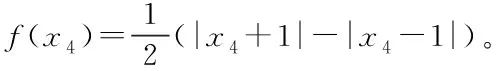
3 算法设计
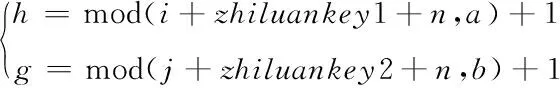
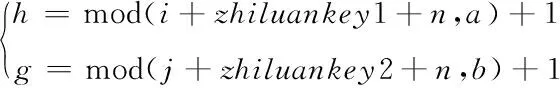
4 性能分析
4.1 直方图
4.2 相关性
4.3 明文敏感性

4.4 密钥敏感性

5 结论

