基于模型验证数据的仿真模型可信度计算方法
孙旭涛,郭小威,王志佳
(中国人民解放军92941部队41分队,辽宁 葫芦岛 125000)
1 引言
仿真[1]凭借组织容易、测控靶标网络要求低、试验成本低、可重复开展等优点,为导弹武器装备提供了大样本仿真手段,为全面评估导弹指标参数提供技术支撑。仿真模型是开展仿真的重要基础,是产生仿真结果的直接因素,仿真模型可信度高低决定着仿真结果的可信性[2]。仿真模型验证是围绕仿真具体仿真目的,采取综合方法对仿真模型与真实系统相似程度的评估过程。在仿真过程中除了关注仿真模型相似度,更关注仿真模型计算结果的可信度,即仿真模型的可信度水平。仿真模型可信度计算一般采取层次分析法、模糊综合评判法、灰色关联分析法等,各种可信度计算方法的思路大致相同,一般均需首先建立树状的可信度指标体系,指标体系的建立往往是比较复杂的[3]。为进一步充分利用模型验证结果,避免建立复杂的可信度评估指标体系,提出一种基于仿真模型验证结果的可信度计算方法。本文在描述模型验证问题基础上,分析了各类模型验证方法,基于模型验证结果提出了仿真模型可信度计算方法,实验结果表明该方法正确合理。
2 模型验证问题形式化描述
模型验证需要对舰空导弹的静态性能和动态性能进行分析验证,导弹的静态性能参数包括杀伤概率、脱靶量等有一定规律的参数,而动态性能参数包括推力、过载、位置、姿态角等没有固定规律的参数,在模型验证过程中就需要对上述参数进行综合分析。如果使用随机变量X表示真实导弹静态性能,则导弹动态性能可看作是随时间变化的静态性能,用一个多维随机过程向量X(t)表示。仿真模型进行模型验证和可信度计算的重要目标是验证与计算模型的静态性能和动态性能,以期达到用评估仿真模型结果来评价导弹相应性能指标。在仿真模型分析计算中,用Y和Y(t)分别表示仿真模型静态性能参数和动态性能参数[4]。
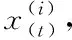
在实际计算中,因为计算设备、存储容量、芯片速度、精度等原因,不可能获取导弹性能的连续变化值,常用的是以固定时间间隔对导弹性能进行采用计算。若对观测到的数据X(t)和Y(t)在固定时间点的采样,则观测数据记为Xn和Yn,其中n=1,2,…,N,N为观测序列长度。静态性能参数和动态性能参数的模型验证可进一步统一为比较时间序列Xn和Yn的一致性。
3 模型验证基本方法
在模型验证形式化描述基础上,模型验证方法就是利用上述数据进行分析计算的过程。目前主要通过定性分析法和定量分析法进行分析论证,定性方法能够给出具体结论,但是缺乏理论数据支撑,定量分析法能够通过详细的数据分析计算给出验证结果,得到越来越多的研究者关注。目前对时间序列Xn和Yn的一致性进行定量分析计算的方法总体分为特征比较法和误差分析法[5]。特征比较法主要思想首先是寻找能够描述序列的典型特征参数,然后分别计算飞行试验序列数据和仿真序列数据的典型特征参数值,最后对两组特征参数值进行分析比较,从而判断两个序列的相似程度。误差分析法是先求得样本序列的误差序列,然后根据误差序列度量指标进行计算,最后对计算的误差序列指标值进行综合分析判断,从而评估两个时间序列的一致性。下面对实践常用的特征比较法和误差分析法分别进行介绍。
特征比较法主要通过时域和频域两个维度来评价,因为时间序列的统计特性都在其概率分布中,n维分布函数族{F1,F2,…,Fn}或概率密度族{f1,f2,…,fn}能够完全确定时间序列的统计特性,因此可以比较两个时间序列的分布函数族或概率密度族特性就能够比较序列的一致性。

(1)

(2)
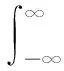
在频域内可以通过各时间序列的平均功率谱分布函数来分析。记随机过程X(t)的谱密度为SX(w),对于任何随机过程X(t),自相关函数RX(t1,t2)的时间均值和功率谱密度互为傅里叶变换,随机过程的谱密度可以通过其自相关函数定义,如式(6)所示
(3)
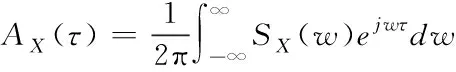
(4)
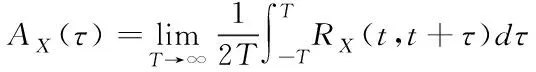
(5)

(6)
基于序列谱密度进行动态性能验证的主要思路是:基于上述随机过程谱密度计算方法,分别对两个序列的功率谱密度进行估计,获得每个频率点的谱估计,然后采用统计假设检验的方法,根据估计值来判断两个频率点功率谱是否相等,最后统计满足频率点功率谱一致的频率点数据,计算谱估计相容性。
误差分析法核心思想是计算两个误差序列的误差,设立能够反映误差水平的误差指标,通过计算这些误差指标来评价仿真模型性能,从而评估两个时间序列的一致性。飞行试验数据序列Xn和仿真时间序列Yn的误差序列为en=Xn-Yn,度量误差序列常用的指标有均方误差、平方和误差、TIC系数等,其计算方法如式(7)到(9)。

(7)
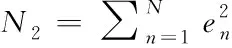
(8)
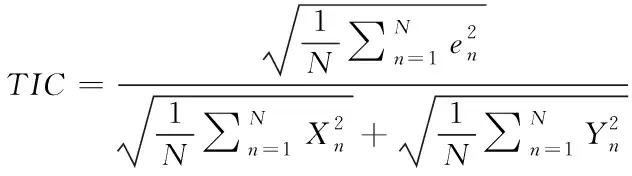
(9)
通过上述时域、频域的特征系数法和误差分析法等定量分析法,能够对飞行试验数据序列Xn和仿真时间序列Yn的一致性水平进行分析评价。
4 基于模型验证数据的可信度计算方法
相关系数和角余弦系数的取值范围为0到1,越接近1表明两个序列的相关性越大,谱估计相容性方法计算结果范围为0到100%,越接近100%表明两个序列相容性越大,TIC系数的取值从0到1,越接近于0表明两个序列越接近。采取相关系数、角余弦系数、谱估计相容性方法和TIC系数等方法,能够对仿真模型性能进行全面而充分的验证。
为进一步充分利用上述模型验证数据,避免建立复杂的可信度评估指标体系,对基于模型验证数据进行可信度评估逐渐成为研究重点。仿真模型验证数据主要包括外场实际飞行试验数据和半实物仿真数据,因此模型验证过程需要采取相同方法对这两类数据分别验证,最后给出导弹模型的可信度。通过特征系数法和误差分析法可以获得两个序列的特征数据,本文综合以上数据提出简单易行的仿真模型可信度计算方法。由于导弹模型与飞行试验数据和半实物试验数据比较方法一致,下面分析时统一称为试验数据。
模型可信度计算方法基本思想为:首先是先计算每个参数的模型验证参数,基于模型验证参数计算单个模型参数的综合验证系数,基于每个参数的综合验证系数和可信度权重计算模型单次可信度,最后对仿真模型可信度计算多次,取多次可信度平均值作为模型的最终可信度。
设仿真共组织M次,每次都要仿真模型各参数进行验证,假设舰空导弹仿真模型需要进行模型验证的参数有K个。对舰空导弹仿真模型进行模型验证的方法是相关系数、角余弦系数、谱估计相容性、TIC系数。用i表示第i次仿真,用k表示第i次仿真中进行模型验证的第k个参数,则第i次模型验证第k个参数的相关系数、角余弦系数、谱估计相容性、TIC系数分别用rik,cik,pik,tik表示。模型验证相关系数、角余弦系数、谱估计相容性、TIC系数等特征系数的判断阈值分别设为rmin,cmin,pmin,tmax。判断阈值是指数据指标满足阈值要求,则数据满足指标要求,否则不满足指标要求。在模型验证定量分析中,如果一项模型验证结果满足阈值指标要求,则验证结果符合要求,否则不符合实际导弹要求。模型验证各参数特性不同,阈值指标也不同,需要根据实际应用需求确定。当然不同情况下阈值指标也不同,需要根据实际舰空导弹仿真模型特定参数需求而设计。设rik,cik,pik,tik的判断阈值分别为rmin,cmin,pmin,tmax,此时单次模型验证结果就是评估rik,cik,pik,tik与阈值rmin,cmin,pmin,tmax之间的大小关系。如果采用严格的模型验证标准,即所有验证系数都要满足阈值要求,则只有在各项评估系数rik,cik,pik,tik都满足阈值rmin,cmin,pmin,tmax要求时,才能够判定此次导弹模型验证结果为合格,即此次模型验证的综合验证结果为合格。
用αik表示第i次仿真第k个参数的综合验证系数,若采用严格的阈值比较方法,综合验证系数的计算方法如式(10)所示。此次模型验证结果为αik,单次模型验证系数rik,cik,pik,tik只有在均满足判断阈值rmin,cmin,pmin,tmax条件时,此次模型综合验证系数才为1,只要有一个条件不满足,综合系数0。根据单次综合验证系数,可以采用综合平均法求解模型可信度,但是这样无法区分各个参数重要程度,因此利用权重方法进行处理。设第k个参数的可信度权重为βk,各个参数的可信度权重值可以相同,也可以不同,可以差距很大,也可以微小差距,通过设置不同的权重,可以根据需求对模型验证和可信度评估关键参数数据凸显。

(10)
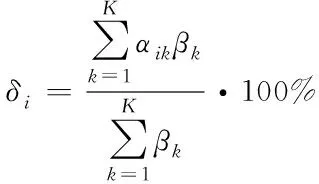
(11)
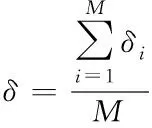
(12)
设第i次模型可信度为δi,基于各参数综合验证系数和可信度权重的单次模型可信度计算方法如式(11),每一次模型验证综合系数与可信度权重相乘,对所有相乘数据求和,最后除以可信度之和,从而计算单次模型可信度。单次模型可信度根据多个参数不同方法验证结果计算而得,能够在一定程度上评估舰空导弹仿真模型可信度水平,但是单次试验结果存在偶然性和误差性,因此需要综合各次试验结果计算仿真模型可信度。设模型可信度为δ,基于各次模型可信度的模型可信度计算方法如式(12)。由于各次仿真模型可信度计算结果地位相当,不存在需要凸显某次试验结果的可能,因此采用综合平均各次可信度计算结果作为最后的舰空导弹仿真模型可信度计算结果。
5 仿真研究
上面分析了基于模型验证数据的导弹模型可信度计算方法,下面以实际案例为例,对提出的仿真模型可信度计算方法进行分析验证。假设模型验证阶段选取导弹8个关键参数,对每个参数分别采取相关系数、角余弦系数、谱估计相容性、TIC系数四种方法进行验证,基于每一次不同方法的模型验证结果计算仿真模型综合验证系数。对仿真模型共进行10次仿真,计算每次仿真模型可信度,根据可信度权重值,综合计算仿真模型可信度。采用相关系数、角余弦系数、谱估计相容性、TIC系数4种特征系数法对仿真模型8个参数进行验证的结果如表1所示。表1表示的是1次模型验证结果,其它9次试验结果与此相同。

表1 一次模型验证结果
假设根据实际应用场景需要,模型验证相关系数、角余弦系数、谱估计相容性、TIC系数等特征系数的判断阈值分别取rmin=0.9,cmin=0.9,pmin=90%,tmax=0.1,采用严格阈值判别方法,则此次模型验证除参数1相关系数小于阈值外,其它各参数的不同验证系数都满足阈值指标要求,因此参数1的综合验证系数为0,其它各参数综合验证系数均为1。
假设参数1到参数7模型可信度权重为1,参数8模型可信度为2,根据式(11)计算单次模型可信度,计算公式如式(13),此次模型可信度计算结果为88.88%。

≈88.88%
(13)
根据10次模型验证结果,分别计算每一次模型可信度,统计10次试验模型可信度计算结果如表2所示。根据式(12)计算仿真模型最终可信度,计算仿真模型的可信度为92.22%。仿真模型可信度是否满足指标要求,再根据实际判别方法进行判断。假设仿真模型可信度达到85%为合格,则仿真模型验证结果证明,仿真模型可信度满足指标要求。
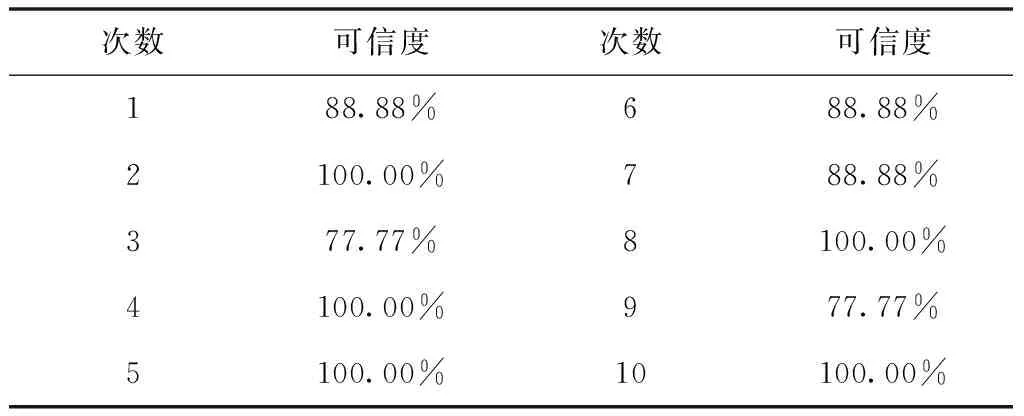
表2 10次模型可信度计算结果
6 结论
模型可信度的高低对舰空导弹仿真模型计算结果可信性具有重要支撑作用,研究导弹模型可信度计算方法,对于全面准确评估导弹效能与性能具有重要意义。本文在导弹模型模型验证数据基础上提出了一种简便易行的导弹模型可信度计算方法,并通过实际案例对方法进行了验证,结果表明了该算法的有效性。提出的基于模型验证数据的可信度计算方法能够充分能够模型验证阶段计算的大量模型验证结果,同时避免仿真模型可信度评估中建立复杂的指标体系。实例结果证明,该方法能够综合利用模型验证数据结果并计算仿真模型可信度,同时充分考虑了各种方法阈值特性和仿真模型各参数权重等特点,是一种计算量少、通用性高的仿真模型可信度计算方法,对全面评估舰空导弹仿真模型可信程度提供了重要途径。

