基于矩阵张量积的轻量网络数据传输加密方法

俞兴木，郑旭飞

(1. 重庆人文科技学院计算机工程学院，重庆 401524；2. 西南大学计算机与信息科学学院，重庆 400715)

1 引言

网络数据传输技术广泛应用在工业、医院和国防等重要领域[1]，传感器是组成无线传感器网络的最小单位，网络规模越大、网络环境越复杂，网络通信过程中所具有的挑战性就越大。随着网络在各个领域的推广，传感器节点所产生的弊端越来越突出，并且在网络传输过程中数据的安全性及隐私性也备受关注[2-4]。

为了提高无线传感器网络通信过程中的效率、安全性及保密性，大量研究者从压缩感知加密方法出发，以此为基础，构建基于压缩感知的数据传输加密算法。文献[5]针对数据传输过程中受到的篡改攻击，基于里德-所罗门码对篡改进行定位，并对数据进行恢复，结合压缩感知轻量级加密方法对终端数据加密，保证数据的保密性，并对测量值进行局部归一化处理，实现能量值的高强度加密，利用压缩感知和RS特性实现数据的双重篡改恢复，实验结果表明该方法具有广泛的适应性。文献[6]设计了由预加密和嵌入两阶段构成的加密方法，通过Arnold置乱和Sine映射所产生的受控矩阵对数据进行加密与压缩，为减少数据所承受的攻击，利用伯恩斯坦多项式对嵌入阶段的密文图像进行处理，将其隐藏到载体图像中，提高加密算法抵抗攻击的能力，实验结果表明，该方法具有较高的安全性。文献[7]采用离散小波变换对数据进行稀疏化处理，基于压缩感知方法加密和测量稀疏矩阵，并加入随机数，对矩阵进行Hilbert置乱操作，将加密后的图像隐藏到载体图像中，实验结果表明，该方法具有较好的鲁棒性，应用范围较广泛。

基于以上研究，压缩感知为网络数据传输的加密技术提供了关键性的支持，可以解决无线网络的安全性和适应性等问题，因此提出基于矩阵张量积的轻量网络数据传输加密方法。基于矩阵张量感知理论，引入辅助矩阵，实现灵活观测信息，结合TCP加密算法，提高数据传输的加密效率与安全性。

2 压缩感知技术

为保证数据采样精度，通常使采样信号的频率高于最高信号频率的两倍，但这种方式采集的信号具有较高的冗余度。为了提高空间的利用率，需要对这些数据进行压缩，然后再进行使用。然而压缩感知不仅可以对稀疏信号降维，还可以通过重构算法将数据恢复成原来的信号。压缩感知过程如图1所示。

图1 压缩感知过程

Rn×nmx

x=Ωa

(1)

其中，a∈Rn×n表示信号x在标准正交变换域Ω中的b个稀疏信号(b表示非零项的个数)，良好的正交变换域可以保证信号稀疏化的效果。

压缩观测的过程中通过测量矩阵Ψ对信号x线性投影，公式可表示为

y=Ψx=ΨΩa=Ζa

(2)

其中，Ψ表示与稀疏矩阵Ω不相关的测量矩阵；Ζ表示感知矩阵。测量矩阵对压缩感知过程中信号精度的恢复有着重要的作用，为了使信号具有唯一性，测量矩阵应满足Spark性质、非相干性质和有限等距原则这三个约束条件。

Spark性质是满足信号重构成功的首要条件，用公式表示为

(3)

相干性质可通过两个列向量的归一化内积最大绝对值表示，公式可表示为

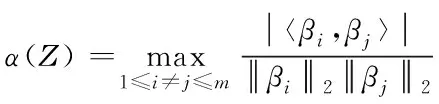
(4)

其中，βi，βj表示任意的两个列向量，α(Ζ)的值越大，表示矩阵列向量相关性越高；反之，相关性越低，因此通过相干性可以构造出较好的指导测量矩阵。

有限等距原则表示若所有b阶稀疏矩阵均小于一个最小常数，那么矩阵Ζ满足b阶有限等距原则，公式可表示为

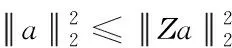
(5)

其中，χb表示约束等距常数。只要满足上述三个约束条件，就可以保证原始信号的重构。信号的重构恢复是将压缩后的低维采样信号恢复为原始信号的过程，公式表示为

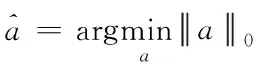
(6)

为了转化成凸优化问题，进一步将公式表示为

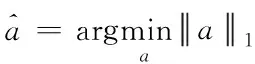
(7)

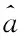
在数据传输过程中，数据信息具有冗余度高和可压缩性等特点，通过数据信息的低采样，降低成本。对于数据的稀疏化操作，本文采用离散小波变换方法，经过稀疏化处理得出信号中较大的非零系数，稀疏处理过程描述如下

A=ΩXΩT

(8)

其中，Ω是稀疏基底矩阵；X是原始传输数据。稀疏处理后的数据，通过测量矩阵压缩观测可表示为

Y=ΨX=ΨΩTAΩ

(9)

其中，Ψ表示测量矩阵；Y表示数据压缩结果。根据重构恢复算法将稀疏后的传输数据进行恢复，并通过逆稀疏化得到原数据。

3 矩阵张量积

压缩感知技术不仅可以对信息进行压缩观测，还能对信息进行加密处理，但加密程度不能抵抗较为严重的攻击。网络数据传输过程中若安全性要求较高，压缩感知技术无法满足安全性的需求，因此需要增加信息的加密强度。本文提出矩阵张量压缩感知方法，不仅可以对不同规模的数据进行观测，还能大大提高数据的安全性。

张量积是矩阵乘法中一种特殊形式，分为左、右张量积，可实现2个任意大小矩阵间的乘法运算。以右张量积为例，假设矩阵C=[c1，c2，…，cn]和矩阵D的维数分别为m×n和p×q，C⊗D那么经过计算后的右张量积可表示为

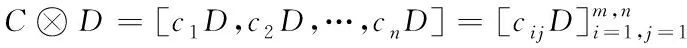
(10)

矩阵张量积运算过程具有矩阵乘法的特性，可以使乘法中的矩阵维数不匹配，即张量积中的左右因式列数与行数不需要相等，这大大提高了矩阵乘法的灵活性。张量压缩感知模型用公式可表示为

y=E×x

(11)

其中，E表示张量观测矩阵；x表示被测量的数据信息；y表示观测值。假定s为左因式列数与右因式行数最小公倍数，进一步将模型表示为

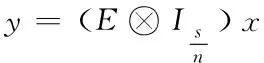
(12)

经过张量积的运算，观测矩阵的维数变大，从理论上表明观测矩阵满足Spark性质、相干性质和有限等距原则。因此可通过矩阵张量压缩感知对传输数据进行压缩与重构。通过构建，本文设计的新模型可表示为

y=γE×x+ηF

(13)

其中，γ和η表示可变参数，E表示原始矩阵；γ表示辅助矩阵。通过调整γ和η的参数值，可以满足不同的需求，使加密后的数据信息具有更高的安全性。原始矩阵可以是任意类型的矩阵，当测量矩阵为可逆矩阵时，可完成数据信息的精准构建，这样可大幅度降低数据节点的存储。辅助矩阵可以是任意类型的矩阵，通过混沌系统产生的矩阵序列具有良好的统计学特性，且服从均匀分布，安全性较高。

原始矩阵通过Tent混沌系统产生，假定系统参数为λE，初始值为zE0，采样间隔为dE。通过采样间隔对数据的采样，可求出随机序列，用公式可表示为

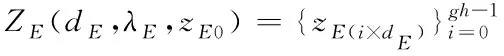
(14)

其中，zE(i×dE)表示第i个随机序列；且满足g=m/p和h=n/p。按照ϖEi=1-2zE(i×dE)对随机序列进行规格化操作，得到的新序列可表示为

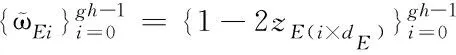
(15)

新序列在区间(-1，1)上均匀分布，通过重新调整结构，可求出原始矩阵E。

辅助矩阵可通过Logistic混沌系统产生，假定系统参数为λF，初始值为zF0，采样间隔为dF。将系统参数和初值代入混沌系统，并按照采样间隔进行采样，可以求出随机序列，用公式可表示为

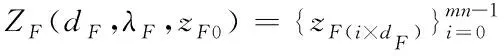
(16)

zF(i×dF)是第i个随机序列。将zF(i×dF)采取规格化处理，得到的新序列如下

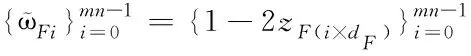
(17)

通过重新调整结构，可求出辅助矩阵F。

以往的重构方法通常是把压缩数据做分割操作，并对分割后的一维信息进行重构，但相邻的数据信息间具有极强的关联性，随着消耗时间的增加，传统方法严重影响了压缩感知性能，因此采用解凸优化问题的方法，将原始数据的稀疏值用公式表示为

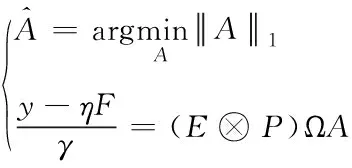
(18)

其中，P表示张量矩阵。该重构算法不仅提高数据重构的效率，还明显改善了数据重构的效果。

4 传输加密算法

在采取对称加密时，加、解密需要共享密钥；在采取非对称加密时，加、解密过程使用不同的密钥。AES技术广泛应用在数据传输过程中，具体实现过程为：发送方对需要加密的传输数据进行加密，通过网络传输将加密后的数据发送给接收方，接收方通过密钥对密文进行解密，得到明文。加密解密过程如图2所示。

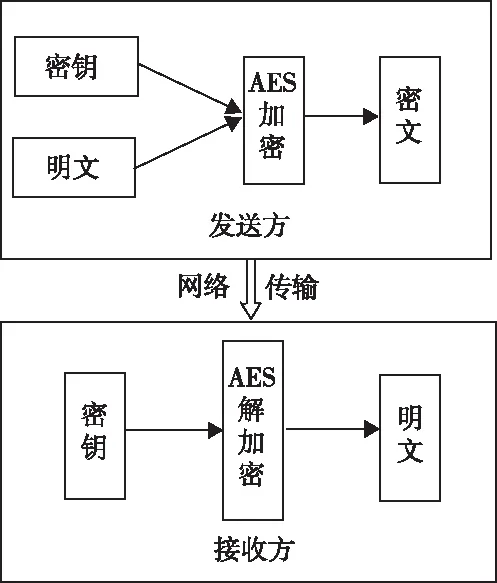
图2 AES加密解密过程

发送方与接收方产生的密钥不能直接传输到网络中，为了提高网络数据传输的安全性，大多情况下密钥通过非对称加密方法对密文加密再传输，因此密钥对网络数据的传输安全具有极其重要的作用，一旦密钥被泄露，攻击者通过密钥便可以窃取数据机密，本文采用对称加密方法对网络传输数据进行加密处理。

AES加密过程是将数据分为多个组，并对每一组进行加密操作，每个组的数据包大小为16个字节，可以选择不同长度的密钥，但密钥长度决定了加密的轮数。AES加密是可逆的，因此AES解密是加密过程的逆过程，通过反序操作即可解密出明文。

数据包属于TCP/IP协议通信中的数据单元，主要由源IP地址、目的IP地址和网络负载数据三部分组成，网络数据传输过程需要对数据进行封装，封装后的数据包发送过程如图3所示。

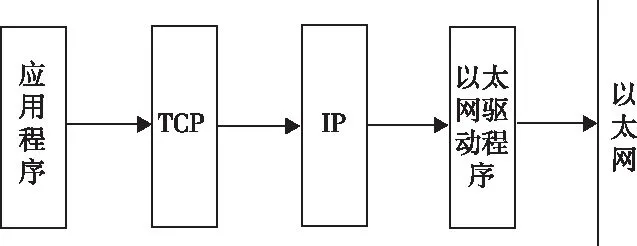
图3 网络数据发送过程

用户数据由数据头和数据体两部分构成，但在网络数据加密传输过程中，通常对数据体进行加密，而对包含版本号、数据长度及数据类型等重要信息的数据头并没有进行加密。那么攻击者窃取包含用户信息的数据头后，会导致网络传输安全性降低，因此采用TCP协议对数据体和数据头同时进行加密。

TCP是IP的传输层协议，每个TCP只能拥有一个发送端和接收端，当数据传输完毕后，需要解释已经建立好的TCP传输连接。由于TCP数据传输过程中的数据段大小由应用层的消息大小和最大传输单元的大小决定，因此TCP段大小具有不确定性。TCP传输通过最大报文段长度判断是否对数据包进行分段处理。若发送的TCP数据较长，则进行分段处理；若发送的TCP数据较短，等缓存中的数据达到一定长度后再进行发送处理。在采用对数据头和数据体加密的过程中，若通过密文方式发送数据头，无法判断出密文的长度，导致接收端无法确定出密文破解的时间，因此采用固定传输大小的方案进行处理。

由AES加密特点，按每组16个字节大小进行分组处理，若数据小于16个字节则对数据填充。TCP传输过程如下：将明文大小固定为1kB，若大于1kB则按数据包形式处理；若小于1kB则填充。通过AES对数据头和数据体进行加密，当接收端收到1kB的数据时进行解密，完成数据的传输。

5 仿真与结果分析

为了验证基于矩阵张量积的轻量网络数据传输加密方法的有效性，在Windows环境中对数据的重构效果与时间消耗两方面进行测试，其中硬件环境包含接收端、发送端和服务器。在对数据的重构效果分析时，采用峰值信噪比对数据重构效果进行评价，峰值信噪比越大，表明数据的重构效果越好。实验中采用3组传输数据，可变参数γ=0.6、η=0.4，经过实验，3组数据在不同压缩比下的峰值信噪比如图4所示。

从图中可以看出，随着压缩比的增加，3组数据的峰值信噪比均有提升，压缩比在0.3～0.4之间的峰值信噪比变化率较大，当压缩比为0.4时，数据的恢复效果依然较好，针对不同数据，随着压缩比的增加，数据的峰值信噪比均呈现相同的变化情况，表明本文提出的方法具有较好的数据恢复效果，并且适用性较为广泛。

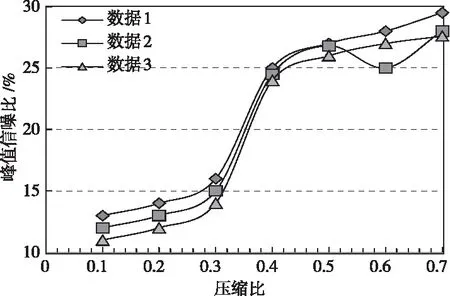
图4 传输数据的压缩比与重构效果图

为了进一步验证本文方法的加密传输效率，通过统计加密与解密时CPU的计算时间来进行数据传输效率的判断。实验仍采用3组传输数据，将仅加密数据体所需要的时间与本文方法进行对比，通过测试CPU计算时间对加密和解密过程进行分析，结果如表1和表2所示。

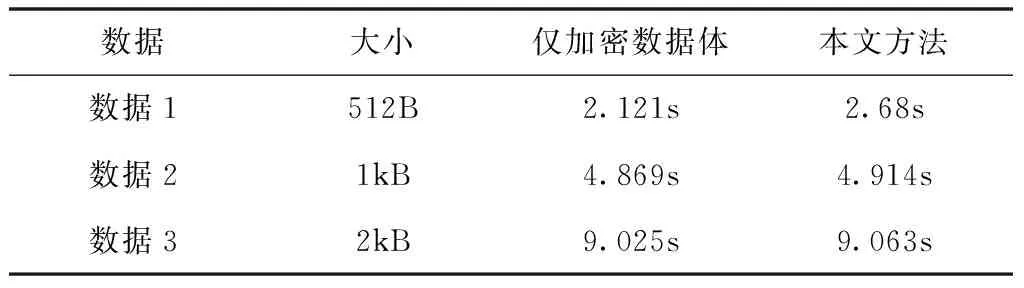
表1 加密过程CPU计算时间

表2 解密过程CPU计算时间

从表中可以看出，本文方法虽然同时对数据体与数据头进行加密，但加密与解密过程CPU计算时间与仅对数据体加密的时间没有很大差别，并且通过对数据头的加密，可以使网络数据在传输过程中具有更高的安全性，通过测试，表明本文方法可以满足网络数据加密与解密传输效率的要求。

6 结束语

为改善压缩感知模型中测量矩阵和被测量信息列数与行数的匹配度，提高压缩感知的安全性，提出矩阵张量积感知模型。由于网络数据传输容易遭受到攻击者对数据信息的窃取，为更好的提高机密效果，采用TPC协议对数据体和数据头进行加密处理。在Windows环境中，选择3组传输数据，对数据的重构效果与时间消耗两方面进行测试。实验结果表明，本文方法压缩比在0.3～0.4之间的峰值信噪比变化率较大，具有较好的适用性，同时对数据体与数据头进行加密，CPU计算时间与仅对数据体加密的时间没有很大差别，说明本文方法完全可以满足网络数据加密与解密传输效率的要求。