强台风作用下低矮建筑结构抗连续性倒塌方法

殷 玥，齐应涛

(西安交通大学人居环境与建筑工程学院，陕西 西安 710000)

1 引言

连续性倒塌描述的是建筑结构中存在的构件在意外事件下出现损伤或破坏，并在外力持续影响下形成的连锁效应，导致建筑结构出现大范围破坏，最终致使建筑物倒塌[1，2]。当建筑结构出现连续性倒塌现象时，会在社会中产生极大的负面影响，并且伴随着人员和财产损失。强台风是造成建筑结构倒塌的主要因素，在目前结构工程研究领域中建筑结构抗连续性倒塌方法成为热门课题。

李晓楠[3]等人针对建筑结构中构件在倒塌事故中的内力分布情况、塑性铰变化情况，在Pushdown分析方法中引入静力分析方法进行整体分析，根据分析结果设计建筑结构抗连续性倒塌方法，该方法没有分析建筑结构的倒塌过程，设计的抗连续性倒塌方法在测试过程中的倒塌率较高，表明方法的整体有效性较差。朱南海[4]等人通过冗余度和易损性对建筑结构失效后的整体性能进行评价，根据评价结果通过削弱易损性低、冗余度高的构件，加强易损性高、冗余度低的构件提高建筑结构的抗连续性倒塌能力，该方法没有构建建筑结构的有限元模型，无法准确地获取建筑结构发生连续性倒塌事故的相关数据，导致建筑结构在外力作用下的相对失效概率较高。孟丽[5]分析了建筑结构的安全储备情况，对倒塌储备系数进行计算，通过增量动力分析法结合倒塌储备系数提高建筑结构的抗连续性倒塌能力系数，该方法无法准确地获得外力作用下建筑物在X方向、Y方向和Z方向的位移变化，进而增加了构建的失效时间，存在位移检测误差大和失效时间长的问题。

为了解决上述方法中存在的问题，提出强台风作用下低矮建筑结构抗连续性倒塌方法，该方法首先构建了有限元模型对低矮建筑结构在强台风作用下的连续性倒塌事故进行分析，获得相关数据，以此为依据提高低矮建筑结构的抗连续性倒塌性能。

2 有限元模型

2.1 建模方法

强台风作用下低矮建筑结构抗连续性倒塌方法通过PKPM软件设计低矮建筑的组合框架，在ABAQUS/Explicit中进行低矮建筑在强台风作用下的连续性倒塌模拟[6]，针对建筑结构中存在的钢筋和相关部件，分别利用桁架单元和实体单元进行模拟。并利用实体单元在软件中构建砌块模型，将内聚力单元插入低矮建筑结构的砌块之间，其主要目的是模拟砌块在强台风作用下产生的砂浆作用。采用面-面接触方法实现核心混凝土与钢管在低矮建筑物中的连接，低矮建筑结构中的互相接触区域通过设置的通用接触线得以识别。

2.2 边界条件

强台风作用下低矮建筑结构抗连续性倒塌方法在GSA准则下设置低矮建筑物梁端的边界条件，在设置边界条件时，需要考虑水平连续拉结作用。

2.3 材料本构关系

1)钢材本构关系

通过下降段的本构模型描述钢材在低矮建筑结构中的本构关系[7，8]，对钢材的软化特征进行反映，钢材本构关系可通过下式进行描述

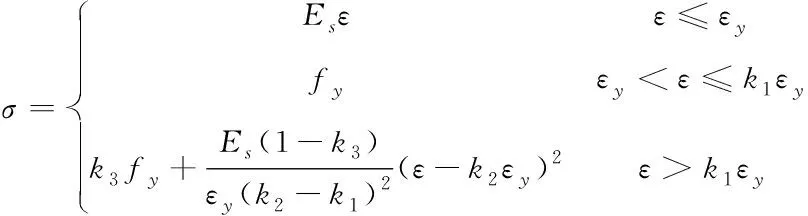
(1)

式中，Es代表的是钢材在低矮建筑结构中的弹性模量；ε代表的是钢材的应变；εy代表的是钢材在低矮建筑结构中的屈服应变；fy代表的是钢材在低矮建筑结构中的屈服强度；参数k1可通过钢材屈服应变与强化段起点应变计算得到；参数k2可通过钢材屈服强度与峰值应变计算得到；参数k3可通过钢材屈服强度与峰值应力计算得到。

2)混凝土本构模型[9，10]

对混凝土在强台风作用下受钢管的约束进行考虑，建立如下本构模型

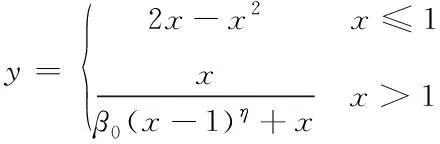
(2)

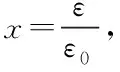
3)填充墙砌块本构模型

通过混凝土塑性损伤模型描述砌块在低矮建筑结构中的本构模型[11，12]，利用下式描述单轴受压砌体本构关系

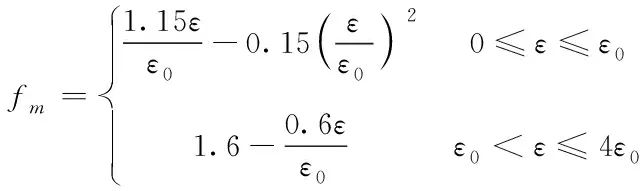
(3)

式中，fm代表的是砌体在低矮建筑结构中抗压强度对应的平均值。

3 抗连续性倒塌方法

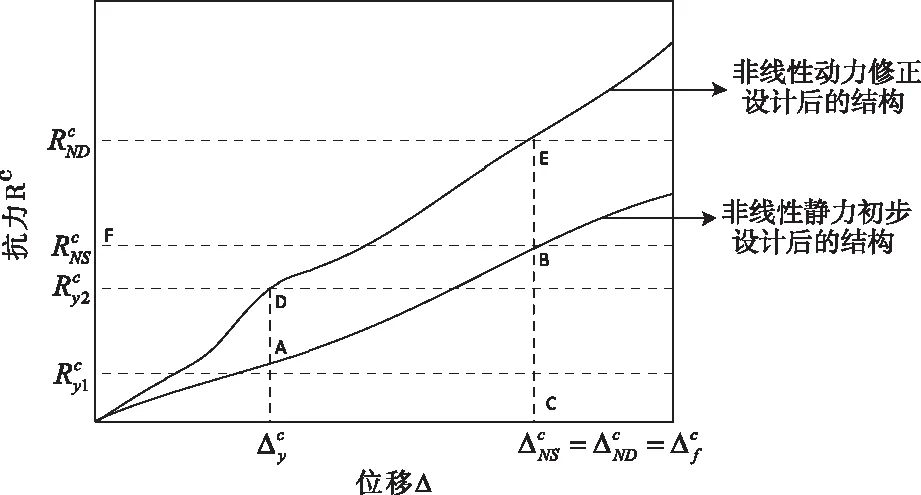
图1 抗力需求

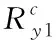
根据能量平衡原理建立能量平衡方程，其表达式如下

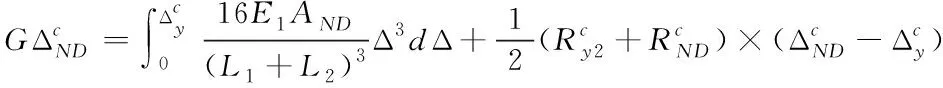
(4)

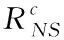
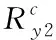
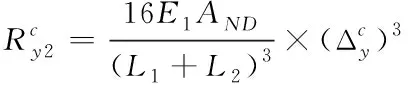
(5)

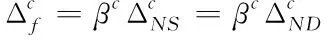
(6)

结合上述内容，获得下述公式

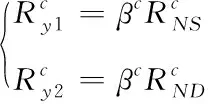
(7)

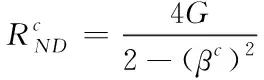
(8)

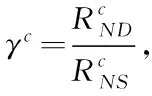
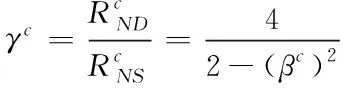
(9)

用Ub表示梁机制在低矮建筑结构中的能耗，其计算公式如下

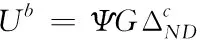
(10)

式中，Ψ代表的是在总能耗中梁机制下能耗所占的比例，即能耗系数。

用γc′表示梁机制能耗后低矮建筑结构非限定动力与静力抗力需求之间存在的关系

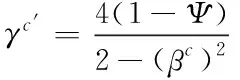
(11)

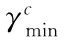
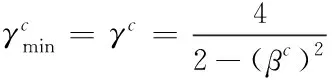
(12)

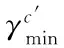
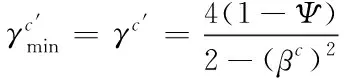
(13)

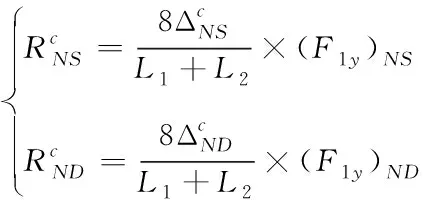
(14)

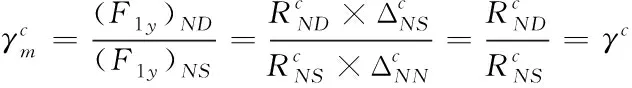
(15)

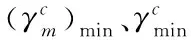
(16)

对上式进行分析可知，低矮建筑结构的抗力需求与构件抗力需求相同，以此为依据实现对低矮建筑结构连续性倒塌设计。

4 实验与分析

为了验证强台风作用下低矮建筑结构抗连续性倒塌方法的整体有效性，需要对其进行测试。

分别采用强台风作用下低矮建筑结构抗连续性倒塌方法、文献[3]方法和文献[4]方法进行抗连续性倒塌测试，对比不同方法的倒塌率Pc，其计算公式如下

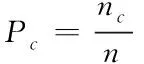
(17)

式中，n代表的是拆除构件总工况数量；nc代表的是出现连续性倒塌的结构数量。

所提方法、文献[3]方法和文献[4]方法的倒塌率如图2所示。

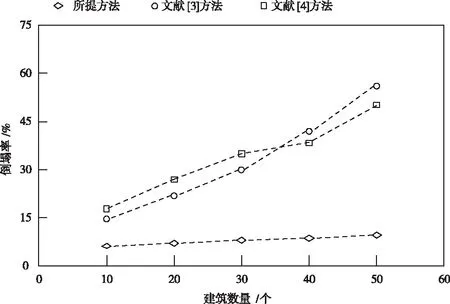
图2 不同方法的倒塌率

倒塌率越高表明方法的抗连续性倒塌能力越弱，相反，倒塌率越低，表明方法的抗连续性倒塌能力越强。对图2中的数据进行分析可知，所提方法、文献[3]方法和文献[4]方法的倒塌率随着建筑数量的增加而增加，对三种方法的测试结果进行分析发现，所提方法的倒塌率上升幅度最小，且均控制在10%以内，文献[3]方法和文献[4]方法在相同建筑数量下获得的倒塌率均高于所提方法，且倒塌率的上升幅度较大，经对比发现，所提方法的倒塌率最小，表明该方法的抗连续性倒塌能力强，因为所提方法构建了有限元模型，对低矮建筑结构的连续性倒塌进行分析，以此为依据设计抗连续性倒塌方法，降低了倒塌率。

将相对失效概率作为指标，对所提方法、文献[3]方法和文献[4]方法进行测试，相对失效概率越低，表明方法的性能越好，不同方法的测试结果如图3所示。

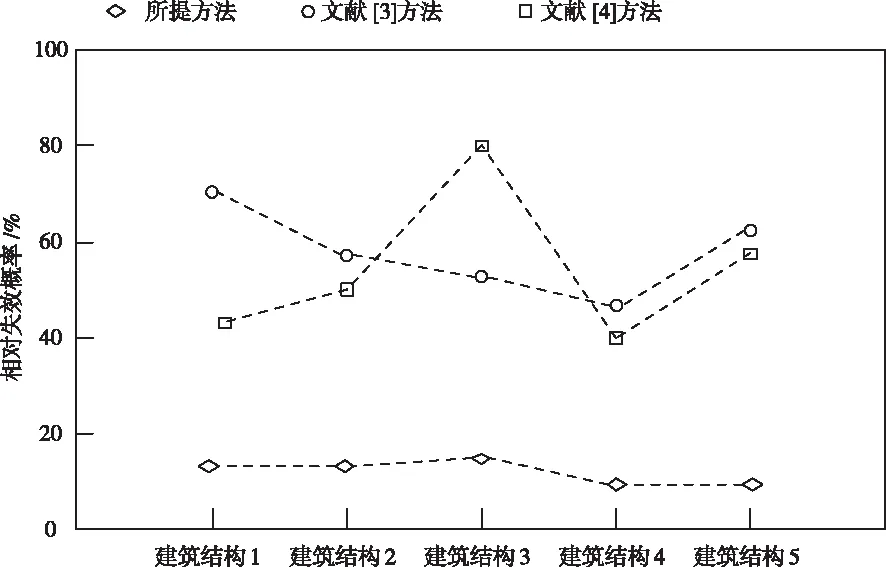
图3 不同方法的相对失效概率

通过五个建筑结构进行测试发现，采用所提方法进行测试时，获得的相对失效概率均在15%以内，采用文献[3]方法对建筑结构1进行测试时，获得的相对失效概率高达70%，采用文献[4]方法建筑结构3进行测试时，获得的相对失效概率高达80%。文献[3]方法和文献[4]方法的相对失效概率较高，表明以上两种方法的抗连续性倒塌性能差，所提方法的相对失效概率低，表明该方法的抗连续性倒塌性能好。

采用所提方法、文献[3]方法和文献[4]方法检测低矮建筑结构在强台风作用下的位移变化，并将检测结果与实际结果进行对比。

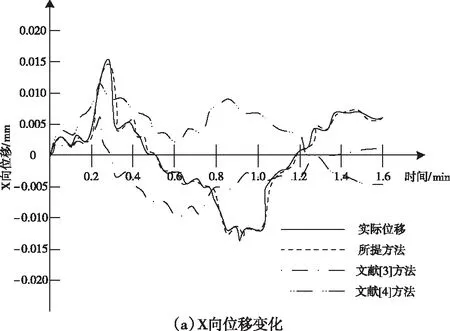
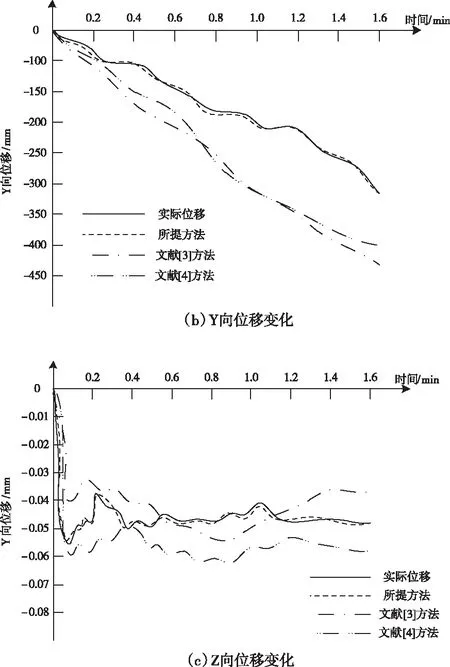
图4 不同方法的位移变化

对图4中的数据进行分析可知，采用所提方法对强台风作用下的低矮建筑结构位移变化进行检测时，获得的检测结果与实际结果基本相符，采用文献[3]方法和文献[4]方法对强台风作用下的低矮建筑结构位移变化进行检测时，获得的检测结果与实际结果之间的偏差较大，通过上述分析可知，所提方法可准确地完成位移检测，为结构抗连续性方法的设计提供相关依据。

在上述测试结果的基础上，在不同强台风风速下测试不同方法作用下的柱失效时间，测试结果如图5所示。

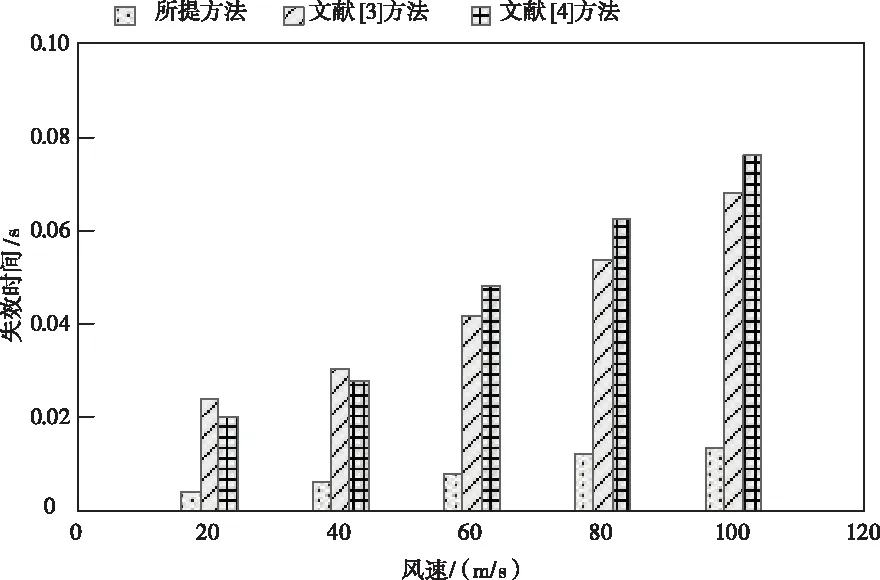
图5 不同方法的失效时间

对图5中的数据进行分析可知，随着风速的增加，不同方法作用下的柱失效时间均有所增长，但在相同风速下，所提方法的柱失效时间均在0.02s以下，远远低于文献[3]方法和文献[4]方法作用下的柱失效时间，失效时间越短，表明方法的有效性越好，验证了所提方法的整体有效性。

5 结束语

低矮建筑结构在强台风作用下容易出现连续性倒塌事故，严重威胁着社会公共安全。目前建筑结构连续性抗倒塌方法存在倒塌率高、相对失效概率高、位移检测误差大和失效时间长的问题，提出强台风作用下低矮建筑结构抗连续性倒塌方法，通过有限元方法模拟倒塌过程，获取相关依据，实现建筑结构抗连续性倒塌方法的设计。经实验证明，所提方法解决了传统方法中存在的问题，提高了低矮建筑结构的安全性，增强了低矮建筑结构在强台风作用下的抗连续性倒塌能力。