球形果蔬表面面积比例不变的投影展开算法研究

王 伟 赵泽群 李 雷 郭树丹 魏超杰 焦艳娜

(1.中国农业大学工学院， 北京 100083； 2.成武县张楼镇政府， 菏泽 274205；3.长沙海关技术中心， 长沙 410004)

0 引言

针对以苹果为主的球形果蔬品质检测主要以外部特征衡量为主，其优劣将直接影响消费者利益，近年来对果蔬外观检测以视觉方式为主[1-2]。通过彩色、深度、红外增强等多类型相机获取表面颜色[3]、纹理[4]、缺陷[5-7]等特征，检测时通常拍摄果蔬表面多幅图像进行区域识别与缺陷检测[8]，取得了较好效果[9-11]。但用于分析的图像往往拍摄角度不全，果蔬表面区域存在遗漏或重复的问题[9-12]，造成表面各处面积识别不准，与面积相关的特征识别准确率较低。

从外观特征来看，这是由于球形果蔬外表面为曲面，各处高斯曲率均为正，无法被平面展开[13-15]，相机无论以何种角度拍摄图像，都会将曲面的球形果蔬外表投影至平面，造成面积变形，影响各处面积占比的衡量效果[16-17]。故为获取符合真实面积比例的果蔬外表面图像，需按照符合面积变换规则的投影方法将球体表面点投影至二维平面，文献[18]利用像素点变换法，根据三维物体的二维阴影由水果图像恢复符合表面真实面积占比的投影图，取得了一定效果，但其仅能针对静态水果。文献[19]提出一种球形果蔬表面积的球带计算法，通过球带面积累加得到球体外表面积，应用于柑橘检测的最大误差为1.32%，但仅使用单一相机，获取的图像覆盖范围较小。文献[20]通过建立图像上点与被测水果上点之间的定量关系，利用像素点变换法实现由三维物体的二维投影图像恢复表面真实几何面积的修正方法，但仍存在检测效率低的问题。

针对现有定面积比例投影方法存在的适用面窄，检测效率低，不能适用于在线检测的问题，本文提出一种适用于在线检测的球形果蔬外表面面积比例不变投影展开算法。首先，在果蔬样品滚动过程中获取多组图像进行拼接展开，随后通过几何变换计算展开图中每一行的理论长度并进行缩放，得到各处面积比例符合真实值的投影图像，并采用标准球进行投影算法准确率验证及最优参数确定，随后选择苹果、脐橙和番茄3种球形果蔬样品以最优参数进行试验，并探索不同样品角度对投影准确率的影响，验证算法可行性。

1 算法实现平台及样品准备

本算法的设计以自主研发的球形果蔬旋转输送装置为平台，针对多种球形果蔬进行检测，由于多种类球形果蔬在近球形外观的基础上仍具有各自特点，且表面颜色分布不均匀，不利于准确计算表面各处面积以衡量算法准确性[21]，故以具有规则颜色分布的标准球为例简化算法，并同步以常见球形果蔬中的苹果为例进行验证算法设计。

1.1 输送机构工作原理

输送机构借助多组旋转式果杯[21]使由前部落入其上的球形果蔬能够以恒定速度滚动前进并被以固定帧速拍摄，获取完整外表面图像，输送机构整体如图1所示，其工作流程为：启动电机令多组果杯沿链条牵引方向往复运动；球形果蔬落入传输机构前部任意两相邻果杯之间，由两侧果杯提供支撑力与摩擦力，随果杯滚动前进；果蔬滚动进入图像采集暗箱内部，触发内部安装的工业相机以固定帧速拍摄果蔬滚动过程中的图像，完成对多幅不同角度的果蔬全表面外观图像获取；果蔬继续滚动离开采集暗箱，随果杯运动至传送机构后部的下落滑槽并离开该平台。

图1 输送机构工作原理图与样机实物图Fig.1 Working principle and prototype of conveying mechanism

1.2 样品准备

用于算法说明的标准球体如图2所示，直径75 mm，表面规则分布红黄相间的条纹，其中黄色色环宽13 mm，占球体表面总面积的35%，剩余红色区域占球体总表面积的65%。用于同步进行算法验证的苹果采用购自北京某商场的红富士苹果。

图2 标准球样品Fig.2 Standard ball sample

2 图像预处理

为实现对球形果蔬外表面各处面积比例不变的完整投影展开，首先需要获取其多角度外表面图像，并对多角度图像中的关键区域进行裁剪和拼接，得到包含其全部外表面信息的展开图，完成图像的预处理[22]。

2.1 多角度图像获取

样品以固定速度滚动前进时，被图像采集暗箱内置的双侧相机以固定帧速同步拍摄获取外观图像。为保证对样品外部图像的完整获取，双相机采用如图3所示的布置方式，每个相机负责一侧样品图像的获取。

由于相机获取的图像中包含待测样品和检测区域背景，故需对样品区域进行提取。如图4所示，根据颜色差异进行色彩空间变换和阈值分割提取轮廓，并裁剪周边像素，只保留包含样品的矩形区域，完成待测样品区域的提取[23]，并以样品轮廓区域最小外接圆直径作为样品直径。

图3 双相机获取图像示意图Fig.3 Image acquisition by dual cameras

图4 样品区域提取步骤Fig.4 Extraction steps of sample area

2.2 多角度图像裁剪与拼接展开

完成不同角度图像中样品区域的提取后，将其拼接以获得外表面的展开图，以标准球和苹果样品为例，拼接的实现流程如图5所示，分别以旋转至不同角度的标准球和苹果图像中的轮廓区域中心点作为基准点[24]，裁剪左右两侧一定宽度的图像为裁剪区域列，该宽度由相机帧速、果杯速度和检测区域长度进行速度匹配得到，公式为

(1)

其中

式中ld——检测区域长度,m

v——样品速度,m/s

D——样品直径,mm

n——相机拍摄帧速，f/s

d——裁剪宽度,mm

裁剪区域反映不同角度下正对相机的样品中心列表面信息，由于相机帧速高，裁剪列窄，故可认为裁剪区域内样品表面为平面，将多列图像按拍摄顺序拼接，得到如图5所示的标准球和苹果外表面展开图，其中苹果外表面粘贴标志色区域用于衡量拼接效果。由于展开图反映样品外表面图像信息不能遗漏或重复，故其宽度应与样品外表面赤道面周长一致，由样品直径决定，此种展开图获取方法保证了样品外表面图像被完整拍摄，其公式为

Cequ=πD

(2)

式中Cequ——样品赤道面周长,mm

图5 多角度图像拼接流程Fig.5 Multi-angle images mosaic process

3 面积比例不变的投影变换

对外表面展开图分析发现，由于展开图中每行像素反映样品垂直于旋转轴的一个窄环形区域图像，图6以标准球滚动过程为例，球体表面垂直于旋转轴的蓝色环形区域被展开为图上的一行像素，且球体表面各处与旋转轴的垂直距离不同，从球体两极点到赤道位置的环区域长度逐渐增大，故图上像素行的宽度也应从上下两边界到中心逐渐增大，但当前展开图中所有像素行的宽度均相同，这使得两极区域面积放大，面积变形明显，因此需要根据每个环形区域长度计算展开图上每个像素行的理论宽度，并对其进行长度缩放以得到无面积变形的投影图。

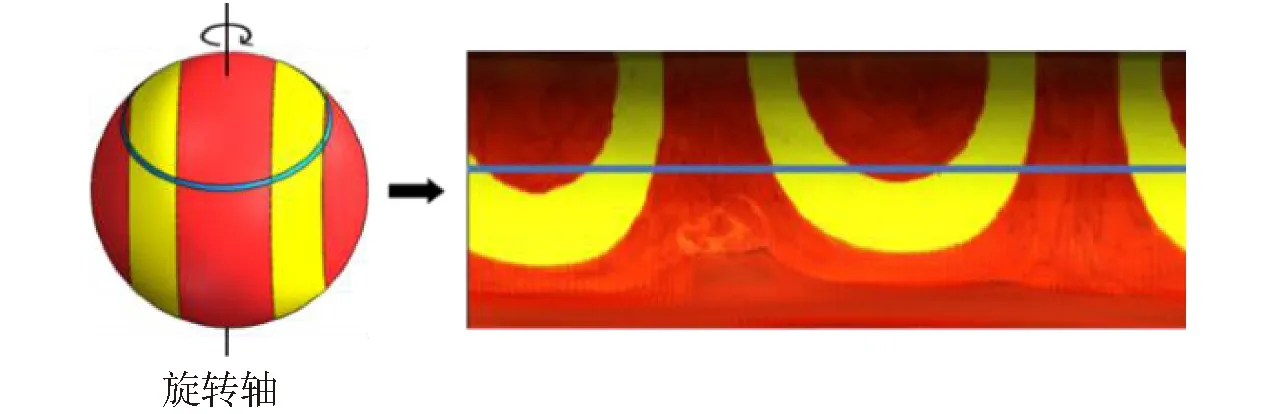
图6 环形表面区域对应展开图Fig.6 Expanded view corresponding to annular area

3.1 投影行宽计算

如图7所示，在获取样品图像时相机与样品的垂直距离为h，水平距离为l，相机方向为图中CO所在直线方向，与水平面夹角为β，点A是相机视野最高点，点B是旋转样品赤道上的点，点C是相机视野中心对应表面点，点D是旋转轴上的点，点E是相机视野内最低点。

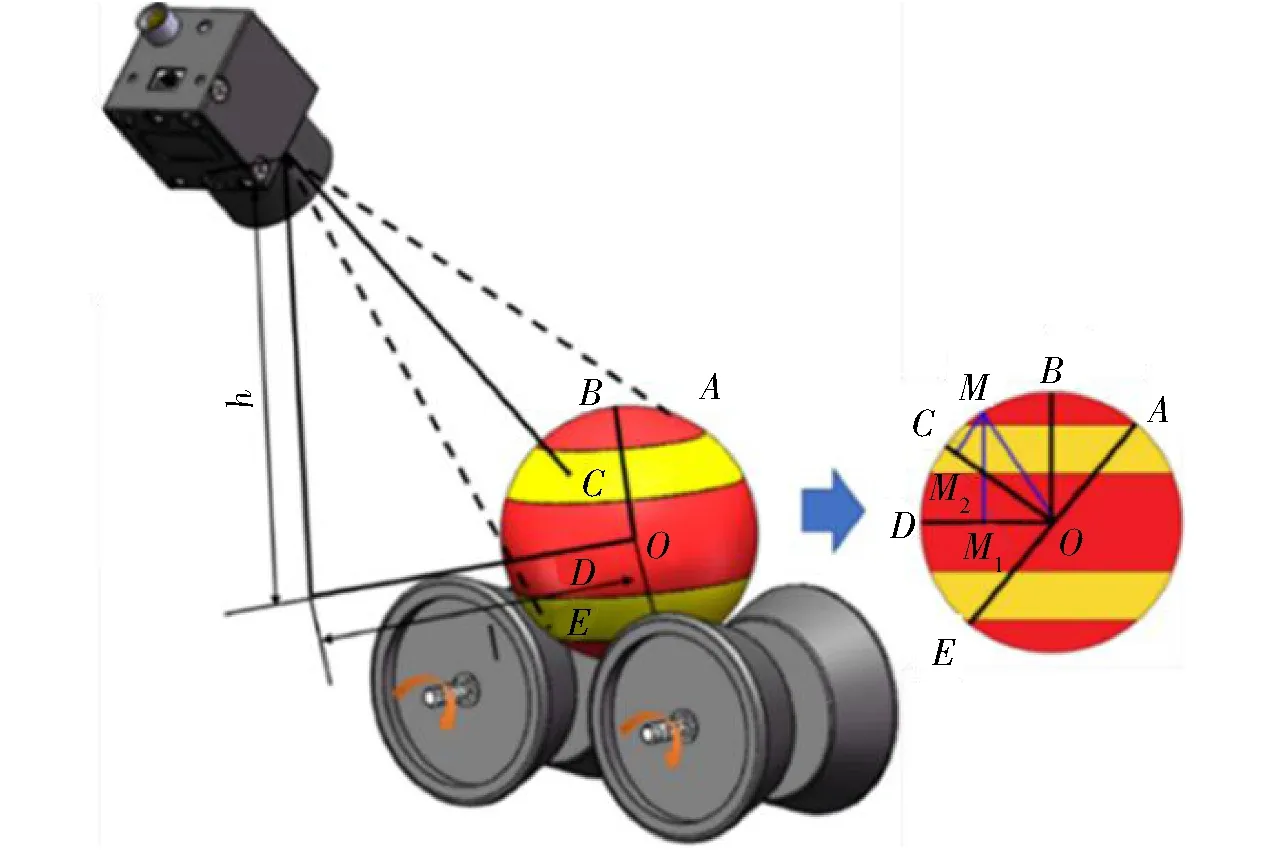
图7 相机拍摄样品方式Fig.7 Camera shooting mode

根据相机获取图像的角度和样品旋转方式，将样品上每一点在展开图中的坐标转换为在样品表面的实际位置。设其表面有一点M，样品滚动时，点M旋转一周经过的距离即为展开图中该点所在行的理论宽度。故通过确定点M的位置，得到其与CO的垂直距离lMM2以及与旋转轴的垂直距离lMM1，即可求得点M所在环形区域长度，即展开图该行图像理论宽度，lMM2计算式为

(3)

其中

式中s——相机与样品间距,mm

ym——点M与中心行坐标像素差,像素

f——相机焦距,mm

H——相机与点M的垂直距离,mm

L——相机与点M的水平距离,mm

在已知lMM2的基础上，确定该样品半径R、相机安装角度β和MO连线与CO夹角α，公式为

(4)

当点M位于样品表面不同位置时，由△MM2O和△MM1O确定的几何关系不同，故lMM1的计算方式不同，具体公式为

(5)

3.2 逐行投影变换

使用已得到的lMM1计算该点所在环形区域的周长，并与前述样品赤道面周长求比，即为该像素行的缩放系数，基于此便可求得该像素行符合真实长度比例的理论投影变换长度Wth，计算式为

Wth=WN

(6)

其中

式中C——切面圆周长,mm

N——像素行缩放系数

W——像素行长度，像素

Wth——像素行理论长度，像素

由计算可知，当点M位于旋转样品赤道表面时，所在垂直于旋转轴的环区域周长最大，即图7中点B对应的展开图中部像素行理论长度最大。而当点M位于旋转样品旋转轴经过的表面时，所在环区域周长最小，即图7中点D对应的展开图上下两边界理论长度最小。图8为投影变换过程，对标准球和苹果样品展开图逐像素行按前述计算的理论长度比例缩放，可保证该行图像中各区域面积占比与真实比例相同，随后对展开图所有行进行此计算并缩放长度，得到一幅与样品外表面各处真实面积比例相同的投影图，可用以衡量果蔬表面颜色占比、缺陷程度等品质。

图8 投影变换过程示意图Fig.8 Projection transformation process

4 图像采集投影试验与结果分析

为验证采集设备和算法的可行性，并求得最优参数，首先依照正交试验原理对标准球进行外表面面积比例不变的投影试验，检测算法准确率并确定最优参数，再以此进行多种果蔬样品的投影试验，衡量装置和算法对不同种果蔬的面积比例不变投影效果。

4.1 标准球试验与分析

由前述投影算法计算流程可知，影响标准球投影效果的主要因素包括：果杯速度、裁剪宽度和相机高度，同时由于样品为均匀球体，进入图像采集装置的滚动方向不会影响图像获取与投影变换精度，故不考虑样品角度对标准球检测准确率的影响，设置试验因素如表1所示。

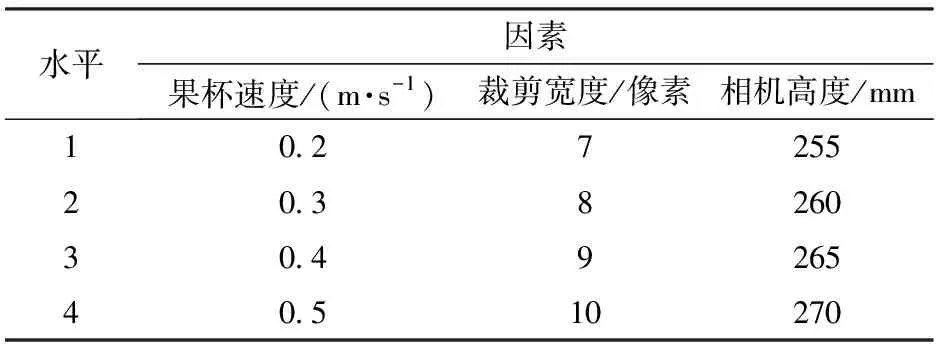
表1 标准球试验因素水平Tab.1 Experiment factors and levels

试验以投影图中样品红黄两色区域面积比与真实面积比的接近程度作为算法准确率的衡量标准，准确率公式为

(7)

式中SY——黄色区域真实面积,mm2

SR——红色区域真实面积,mm2

SYt——图像中黄色区域面积，像素

SRt——图像中红色区域面积，像素

根据各因素水平，利用Design-Expert 8.0软件进行Taguchi OA设计[25-26]，选择L16(34)设计表，探究主要影响因素、优水平和优组合，并使用方差分析验证各因素对试验指标影响的显著性，拟合一般线性模型的回归方程[23]。

表2中A、B、C分别表示果杯速度、裁剪宽度、相机高度水平值，由表2确定试验各单因素水平与检测准确率关系，其中检测准确率随果杯速度和裁剪宽度增加时先上升后下降，随相机高度增加时持续下降，控制三因素的最优水平分别为0.4 m/s、9像素、255 mm。

对Taguchi OA试验结果方差分析如表3所示，

表2 Taguchi OA试验设计与结果Tab.2 Taguchi OA design and results

表3 试验结果方差分析Tab.3 Analysis of variance and experimental results

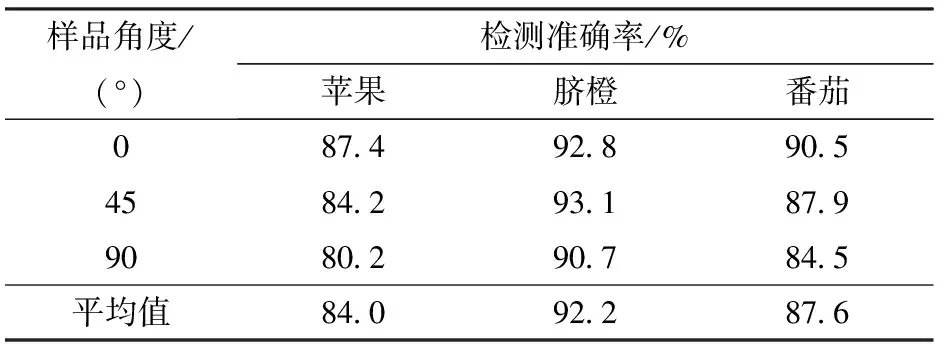
三因素中最大和最小特征平均数差由大到小依次为A、B、C，即各因素影响主次为A、B、C。方差分析并拟合一般线性模型的回归方程可知，因素A和B对试验指标的影响都达到极显著水平(P<0.01),因素C对试验指标的影响达到显著水平(0.01

Yglobal=90.25+0.492A+0.684B-0.554C

(8)

4.2 基于球形果蔬的算法适用性验证

4.2.1试验设计与方法

为验证算法针对真实球形果蔬表面投影的准确率，以苹果、脐橙和番茄3种球形果蔬作为试验对象，基于已得出的标准球因素最优组合进行试验，由于果蔬种类和成熟度不同，无法在多种样品中找到一种通用的面积区域衡量标准，故在样品表面人工涂抹两块与果蔬主体颜色区分明显的矩形标志区域A和B作为参照，面积之比为1∶1.5，如图9所示。分别计算两两标志色区域之间的面积比与真实值的接近程度以衡量算法的准确率，计算公式为

(9)

式中SA——测得样品表面A区域面积

SB——测得样品表面B区域面积

SAt——样品表面A区域理论面积

SBt——样品表面B区域理论面积

图9 果蔬样品粘贴标志色示例Fig.9 Example of sticking logo color for samples

同时考虑到果蔬球形外观的不规则性，设定果梗花萼方向平行于果杯旋转轴为0°，垂直于果杯旋转轴为90°，使待测果蔬样品以0°、45°和90°进入图像采集设备进行检测，如图10所示，探究滚动过程中采集图像的角度对果蔬样品投影准确率的影响。

图10 不同样品角度滚动示意图Fig.10 Different sample rolling angles

4.2.2试验结果与分析

对苹果、脐橙和番茄样品以3种不同角度分别进行30次检测，投影变换结果如图11所示，总体检测准确率平均值如表4所示。

图11 3种样品投影图Fig.11 Projections of three sample

分析发现对3种果蔬的表面面积比例不变投影展开的平均准确率分别达到84.0%、92.2%和87.6%，脐橙检测准确率最高，达到92.2%，苹果检测准确率最低，为84.0%，算法针对不同种球形果蔬的适用效果不同，现以球形度反映样品外形与正球形的接近程度，从果蔬外观特点来看，脐橙多为球形或椭球形，且表面光洁，仅在果梗部位稍有突起，外形球形度最好，故其检测准确率最高。番茄则多为扁球形，仅在果梗位置出现凹陷，整体球形度也较好，其检测准确率稍低。而苹果外形多为花萼处较窄、果梗处稍宽的椭球形，且两端有隆起，花萼下陷，球形度最差，故其检测准确率最低，表明算法能够满足对球形果蔬外表面展开面积比例不变的要求，但检测效果与果蔬外形相关性高，在检测时外形球形度越好的果蔬品种准确率越高。

表4 3种样品检测准确率平均值Tab.4 Average of detection accuracy of three samples

同时，同种样品在不同滚动角度检测准确率也不同，由表4可得，苹果、脐橙和番茄均以样品角度0°检测时的准确率最高，90°时最低，故以样品角度0°为检测结果的最佳指标，将3种样品45°与90°的各30次检测结果与之对比，建立如图12所示的误差箱线图。

图12 与最优指标对比误差箱线Fig.12 Error boxplot compared with optimal indicator

从图12发现，3种样品中脐橙的检测误差最小，且样品角度45°与90°检测差异不大，稳定性较好。而苹果和番茄对比0°最优指标时，在45°与90°分别出现了明显差异，均表现为45°所对应的误差和误差的分布范围明显小于90°，即样品沿45°滚动时检测准确率和稳定性都高于90°，这是由于样品的滚动角度越接近以果梗花萼所在直线为旋转轴时，侧向安装的相机拍摄的图像为苹果的果梗和花萼面，具有更接近正圆形的轮廓，由于所利用的外部品质检测算法是以正球形样品为基础建立的，故此轮廓更适合于中心区域的提取与拼接投影，检测准确率较高，而苹果以更接近垂直于果梗花萼直线的轴为旋转轴时，则相机拍摄为苹果侧面区域，轮廓接近椭圆，导致投影算法准确率降低。

5 结论

(1)利用球形果蔬便于旋转的特性，设计图像裁剪与拼接实现果蔬外表面的二维展开，依照旋转过程中的图像获取方式设计一种保证果蔬外表面展开图各处面积比例与真实值一致的投影变换方法，用于颜色、缺陷区域的面积识别。

(2)通过具有规则颜色分布的标准球样品进行投影算法准确率的衡量和最优参数的确定，以裁剪宽度、果杯速度和相机高度作为三因素进行正交试验，建立回归模型，结果表明，三因素对投影算法准确度影响均达到显著水平，当果杯速度0.40 m/s、裁剪宽度9像素、相机高度255 mm时试验结果最好，准确率为95.64%，以此参数进行苹果、脐橙和番茄3种果蔬的检测，其检测准确率分别达到84.0%、92.2%和87.6%，验证了整机和算法设计的合理性，并引入样品不同角度对检测的影响，发现被相机获取的轮廓越接近圆形，越便于准确拼接图像的获取和检测准确率的提高。