螺旋推进器影响多功率微波加热系统加热均匀性的仿真分析

李昊儒，刘 杰，孟祥文,何 燕

(青岛科技大学 机电工程学院，山东 青岛 266110)

1 引 言

微波加热方式相较于传统加热方式是一种内部加热的方法，具有加热速度快、节能高效、易于控制、降低污染等特点[1-2]，被广泛地应用于食品加工、化学工程与物料干燥等领域[3]。但存在加热效率低、出现“热点”和热失控等问题，严重时会烧坏微波发生器和反应物，造成重大安全事故[4]。因此，提高微波加热过程中加热的均匀性成为研究微波加热的重点内容。工业中微波加热设备通常采用多功率馈口的形式[5]，本文通过对多功率微波加热设备进行多物理场仿真，改善微波加热过程中由能量分布不集中造成加热不均匀的问题。

本文以水作为加热材料为例，在多功率微波加热设备中加入螺旋输送器。工作时螺旋输送器旋转带动水向轴向和径向运动，使得水不会一直处于磁场较强或磁场较弱的位置，能够更好地吸收微波散能，提高装置内水温度的均匀性，实现微波有效利用加热更加均匀的目的。通过改变入口速度和螺旋转速探究不同流速不同螺旋转速对加热均匀性的影响，同时对比了不同材料对加热均匀性的影响。

多物理场仿真是计算微波加热的有效手段[6]，在COMSOL Multiphysics仿真软件中，可实现介电系数随温度变化和电磁场更新求解的全耦合计算，非常适用于微波加热过程的全耦合计算。

2 计算模型与方法

2.1 几何模型

图1的模型结构为本文的仿真计算模型，微波腔体为正六边体结构。腔体六边形边长为200 mm，长410 mm。微波波导采用型号BJ-22的波导，长109.2 mm宽54.6 mm高50 mm，位于六个侧面正中间，呈正交分布。螺旋输送器内径20 mm，外径100 mm，螺距160 mm，位于微波腔体的中心、外套直径为120 mm的管道。液体从管道一侧流入经螺旋输送器从另一侧流出。每个微波功率为1 kW，端口激励模式为TE10模，频率为2.45 GHz。加热时间30 s，时间步长设为0.1 s。

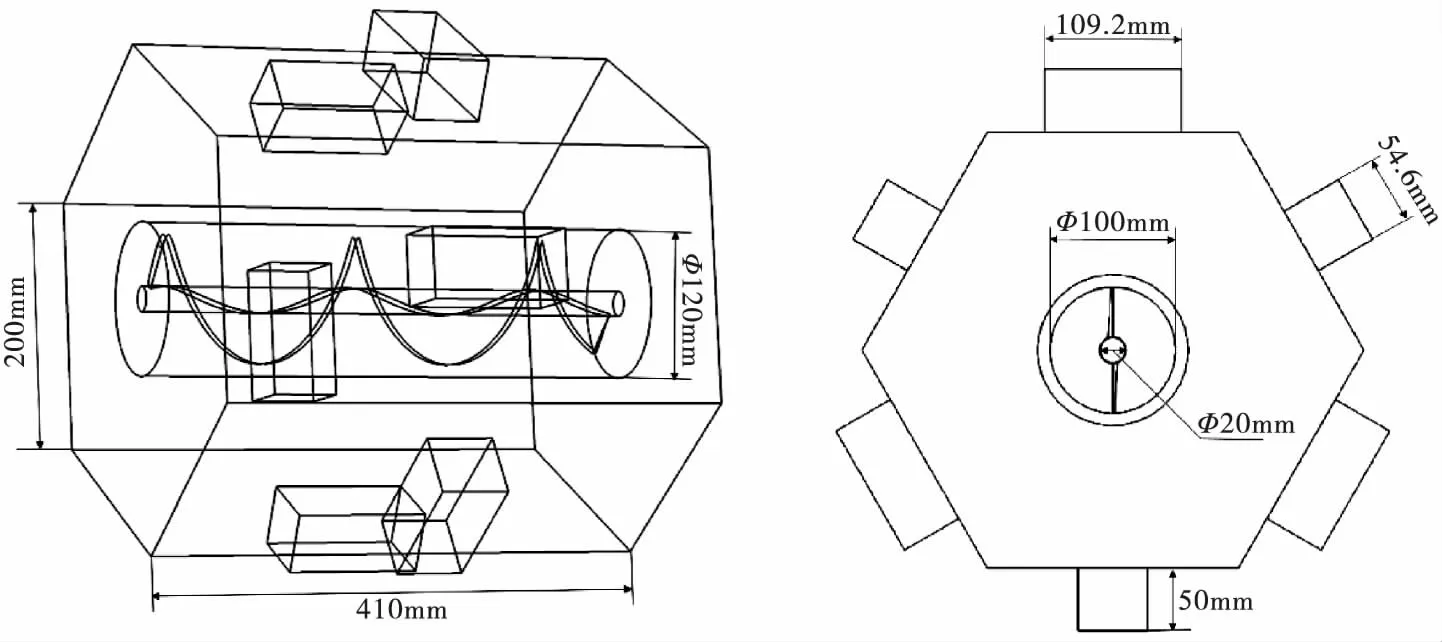
图1 微波加热装置模型图

2.2 控制方程

在此模型中，通过耦合电磁波-频域、流体传热、机械旋转-层流或湍流和动网格接口进行微波加热流体的仿真计算。在电磁模块，求解麦克斯韦方程计算电场强度[7-8]，方程如下：

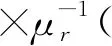
(1)

式中：ω为角频率(ω=2πf)，rad/s；ε0为真空介电常数，F/m；εr为相对介电常数；μr为相对磁导率；c0为真空光速，m/s；σ为电导率，s/m；E为电场强度。

在传热模块中，通过如下流体传热方程计算温度场的分布：

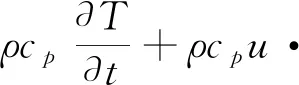
(2)

q=-k∇T

(3)

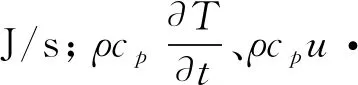
在流体场模块，流体属于不可压缩流体，根据流体运动状态可分为层流运动和湍流运动，当流体处于层流状态时，其计算方程如下：

ρ(u·∇)u=∇·(-pI+K)+F

(4)

ρ∇·u=0

(5)

当流体处于湍流状态时，计算方程如下：

ρ(u·∇)u=∇·(-pI+K)+F

(6)

ρ∇·u=0

(7)

K=(μ+μT)(∇u+(∇u)T)

(8)

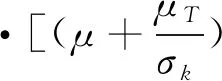
(9)

ρ(u·∇)=∇∇=ep

(10)

(11)

pk=μT[∇u∶(∇u+(∇u)T)]

(12)

式中：p为压力，Pa；F为体应力张量；I为单位张量；为湍流散耗率；k为湍流动能，；μT为湍流黏性系数；pk为雷诺应力；c、c、cμ、σk为湍流k-ε模型的经验系数。

根据搅拌槽的雷诺数公式[9-10]确定采用层流计算模型或湍流计算模型，搅拌槽的雷诺数计算公式如下：

(13)

式中：ρm为液体密度，1 000 kg/m3；N为螺旋转速，r/s；D为螺旋输送器直径，0.1 m；μ为液体的动力黏度，约0.001 Pa·s。当螺旋转速N为0.2 r/s时，管道内雷诺数小于2 300，可采用层流计算模型，当螺旋转速为0.3 r/s时，管道内雷诺数大于2 300，可采用湍流计算模型。

2.3 边界条件

本文所用模型除六个微波激励端口外，其余边界均为理想电导体，每个激励端口输入功率分别为1 000 W，激励模式为TE10模，频率为2.45 GHz。流体管道壁设为无滑移壁，一致边界对设为连续流动性，出口压力为0，无黏滞应力边界。为简化计算忽略流体与螺旋输送器的热交换，忽略流体辐射散热。材料初始温度均设为20 ℃。

2.4 网格质量

将用户控制网格划分为几何体网格。为得到精确结果，最大网格尺寸精确到波长的十分之一。网格划分如图2所示，平均单元质量为0.661 9。当平均网格质量大于0.6时，可认为结果是可靠的[11]。

图2 网格单元

3 结果与讨论

3.1 不同螺旋转速对温度均匀性的影响

将流体入口出口边界均设置为开放性边界，管道内流体速度只由螺旋输送器旋转转速决定。这里只考虑微波加热造成的不均匀性不考虑水的蒸发，允许水的最大温度超过其沸点。本文采用温度变异系数COV来表征流体加热的均匀性[12]，计算公式如式(14)所示，COV是温度标准差与平均温度升高值的比值，能够排除可能由于整体温升不明显而造成的均匀性高的假象，更加客观地表现出数据的离散程度[13]。COV值越小，表示其温度均匀性越高。

(14)

式中：Ti为加热结束后任一点的温度， ℃；ΔT为加热结束后的平均温度， ℃；T0为初始温度， ℃。

在不同螺旋转速下加热30 s得到管道水平截面温度分布图如图3所示。

图3 不同螺旋转速加热30 s后管道水平截面温度示意图

由图3可知，当螺旋转速为0，即水静止时，温度分布最不均匀。这是由于电磁场分布不均匀，不同位置的水吸收到的能量也有多有少，处于热点位置的水吸收的能量会比其他位置的水吸收的能量更多，导致场强高的位置温度高。图4是加热30 s后不同转速对应整个管道的COV以及平均温度曲线。随着螺旋转速的提高，流体在螺旋的扰动推进下流速也会加快，管道内流体的平均温度随着转速的提高而降低，转速越高，平均温度降低得越慢，说明随着转速增加到一定程度，提高转速对管道内平均温度的影响不大。

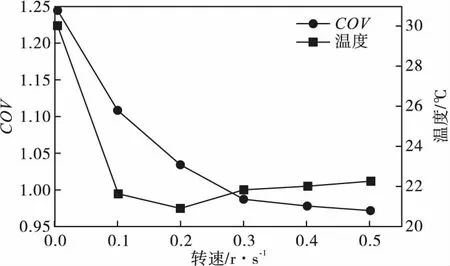
图4 不同螺旋转速加热30 s后对应的COV曲线与平均温度

管道的温度变异系数随着螺旋转速的增加呈现先减小后增加的趋势。螺旋转速小于0.2 r/s时，增加螺旋转速对温度变异系数影响较大，螺旋转速大于0.2 r/s时，增加螺旋转速会提高温度变异系数。当螺旋转速为0，即水静止时，加热30 s温度变异系数为1.223 67。在螺旋转速为0.2 r/s时，温度变异系数最低，此时COV值为0.975 16。螺旋推进器旋转对提高管道内温度均匀性起促进作用，仿真中温度变异系数最高提升了20.31%。

3.2 不同入口速度对温度均匀性的影响

当流体以不同流速流螺旋管道时，螺旋推进器的搅动会使流体有更复杂的流动。本节选取螺旋的转速分别为0、0.1、0.2 r/s，仿真对比了层流状态下不同入口速度对加热均匀性的影响。

图5(a)展示了不同螺旋转速在加热30 s时管内流体平均温度在不同入口流速下的变化，相同的入口流速下螺旋转速快会加快管道内流体流速，螺旋转速越快，平均温度越低。相同螺旋转速下，随着入口流速的增加平均温度呈先快速下降后缓慢下降的趋势，且螺旋转速对温度的影响程度逐渐变小。在入口流速为0.06 m/s时，三种螺旋转速下的平均温度均在21.2 ℃左右。图5(b)是30 s时不同流速下管内COV变化曲线。当螺旋转速为0时，COV先降低后增加，在入口流速为0.04 m/s时，温度变异系数最小为0.997 5。流速在0.03～0.06 m/s范围内COV变化不大。当螺旋旋转时，管内流体在入口速度和螺旋转速的作用下流动更复杂。螺旋转速越大，COV值的变化范围也越大。管道温度变异系数最小出现在入口流速0.01 m/s螺旋转速0.2 r/s时，最小为0.910 1，此时管道内流体平均温度较高，加热均匀性最好。

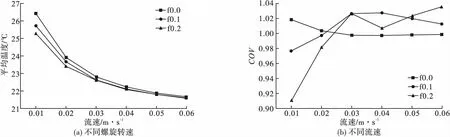
图5 加热30 s后不同流速不同转速下平均温度和COV曲线

图6展示了不同螺旋转速温度变异系数在不同入口流速下随时间变化的曲面图。

图6 温度变异系数随时间流速变化曲面图

由图6中可以看出温度变异系数随时间变化逐渐降低，但也会受到流速和螺旋转速的影响。当螺旋转速为0，即螺旋静止时，随着入口流速的增大温度变异系数随时间变化曲线逐渐呈现出先减小后增加趋势，增加幅度很小。当螺旋转速为0.1 r/s时，流速小于0.03 m/s时温度变异系数随时间变化曲线逐渐降低；流速大于等于0.03 m/s时，温度变异系数随时间变化曲线先降低后在一个小范围内震荡变化，且流速越大出现震荡变化的时间越早。当螺旋转速为0.2 r/s时，相同流速下出现震荡变化的时间更早，且震荡幅度更大。

3.3 不同螺旋材料对温度均匀性的影响

介电损耗不同的材料对微波的吸收能力不同，本节仿真对比了用两种吸收能力不同材料的螺旋输送器对温度均匀性的影响，一种是微波反射型材料铝，一种是微波穿透型材料聚四氟乙烯，其介电常数为2.55[14]。在加热30 s后对比不同材料的螺旋输送器在不同转速下的管道内温度变异系数和平均温度，流体出入口均为开放边界。观察图7可知，使用铝材料作螺旋输送器在相同转速下要比使用聚四氟乙烯作螺旋输送器的温度变异系数要低，即螺旋输送器使用铝材料比使用聚四氟乙烯材料加热更均匀。铝材料作螺旋输送器在相同转速下要比聚四氟乙烯作螺旋输送器有更高的平均温度，在水静止时温度相差最大，最大温差有0.634 ℃。随着螺旋转速的增加，流体在管道内停留的时间相应减少，平均温度会降低，同时不同材料的螺旋输送器对平均温度的影响也会降低，两种材料的平均温度温差随着转速的增加逐渐减少。微波反射型材料比微波透射型材料更能提高温度的均匀性。

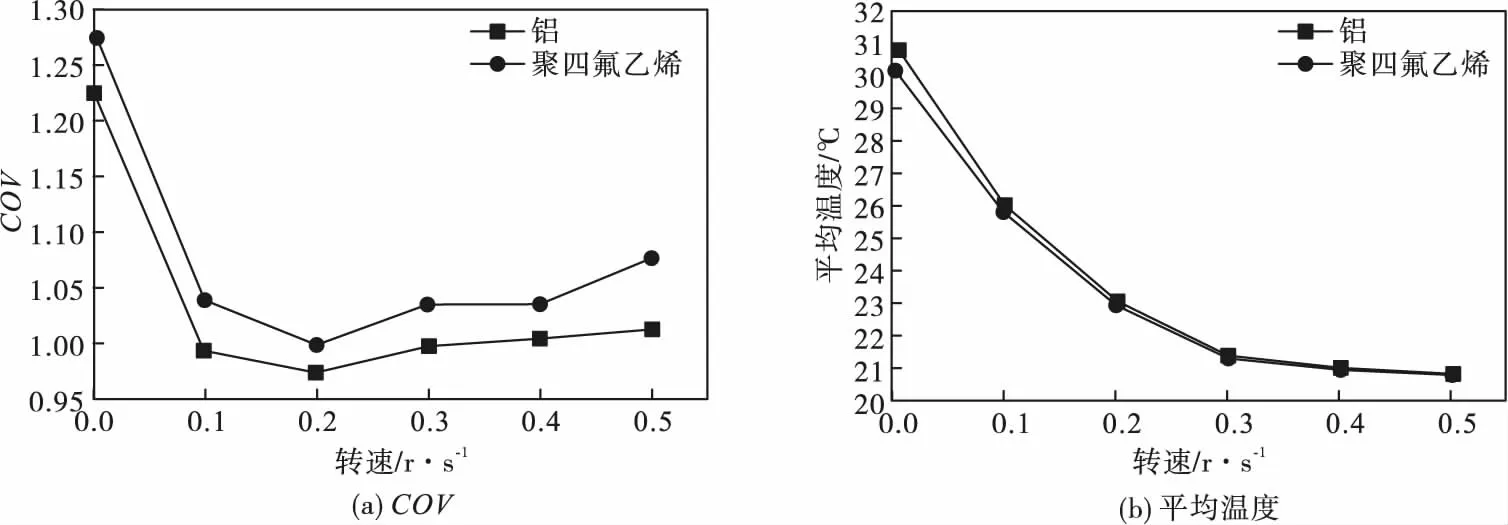
图7 加热30 s后不同材料的螺旋在不同转速下的COV和平均温度

4 结 论

本文通过动网格结合多物理场耦合实现了搅拌流动液体的仿真计算。以水为例、以螺旋推进器为搅拌装置进行研究，通过改变螺旋推进器的转速改变流体的流动状态，得到以下结论：

(1)当流动状态为层流时，水的微波加热均匀性与螺旋转速呈负相关，转速越大加热均匀性越好；当流动状态为湍流时，水的微波加热均匀性与螺旋转速呈正相关，在一定转速范围内，转速增大加热均匀性越差。

(2)相同情况下，螺旋推进器采用微波反射型材料铝的加热均匀性要优于微波投射型材料聚四氟乙烯，随着螺旋转速的增加，材料引起的流体平均温度的差异会逐渐减小。

(3)受入口流速和螺旋转速的影响，水的加热均匀性COV值随时间先减小后再在一定范围内波动。本文采用的模型入口流速为0.01 m/s,螺旋转速0.2 r/s时，加热效果最好。螺旋转速过大不利于流体的持续加热，因此需要选择合理的螺旋转速。

上述结论阐明了转速和流速影响微波加热的一般规律，为实际工业设计提供重要理论参考。